隧道掘进机撑靴导致洞壁破坏机理的研究

李泰灃，郑婕，张千里，李涛

（1.中国铁道科学研究院，北京100081；2.北京交通大学土木建筑工程学院，北京100044；3.中国铁道科学研究院铁道建筑研究所，北京100081）

隧道掘进机撑靴导致洞壁破坏机理的研究

李泰灃1，郑婕2，张千里3，李涛2

（1.中国铁道科学研究院，北京100081；2.北京交通大学土木建筑工程学院，北京100044；3.中国铁道科学研究院铁道建筑研究所，北京100081）

考虑隧道埋深、隧道洞径和围岩强度3种影响因素，采用有限元软件ABAQUS建模，分析了全断面隧道掘进机撑靴与隧道围岩的相互作用、围岩变形和破坏的规律，并与实测结果进行了对比。结果表明:随隧道埋深的增加，隧道围岩的稳定性逐渐增强；随着隧道洞径的增大，隧道围岩的稳定性逐渐降低，但变化幅度较小；随着隧道围岩抗剪强度的降低，在撑靴荷载作用下隧道围岩的承载力逐渐降低，建议实际工程中隧道围岩的内摩擦角不能小于45°；3种影响因素中，隧道围岩的稳定性对于围岩强度的变化最为敏感，其次是隧道埋深，最后为隧道洞径；辽西北供水工程实测单侧撑靴支撑力为24 900～25 900 kN，可推断出单侧撑靴径向应力为5.72～5.95 MPa，与仿真计算结果一致。

全断面隧道掘进机；撑靴；隧道围岩；破坏模式；隧道施工；数值模拟

全断面隧道掘进机（Tunnel Boring Machine，TBM）是集机械、电子、液压、激光技术于一体的大型集成化隧道施工作业系统［1］。TBM属于按需求定制的产品和系统，结合每个TBM隧道工程的特点、条件和技术问题，采用不同的TBM系统集成设计与施工技术方案，既需要有个性的考虑，又需要作出共性的总结［2］。其中，TBM推进和撑靴系统在TBM隧道工程施工中发挥着至关重要的作用。撑靴作为TBM的固定部分，掘进时靠其支撑整机重量，并将推力和扭矩反力传递给洞壁，借助球形绞均匀地支撑在洞壁上，避免引起集中载荷对洞壁的破坏［3］。然而，对于TBM推进和撑靴系统在隧道施工中与隧道围岩的相互作用机理目前研究尚少，也主要依赖于工程经验指导实际施工。

隧道围岩的破坏受多种因素的综合影响，可概括为3种：①地质因素，包括岩石物理力学性质、结构面的抗剪特性、地下水作用、风化作用等；②工程因素，包括隧道埋深和断面的形状、大小、高跨比等；③施工因素，包括隧道施工方法和手段、支护时间和方式等［4-9］。本文以辽西北供水工程为例，考虑隧道埋深、隧道洞径和围岩强度3种影响因素，采用有限元软件ABAQUS建模［10］，对TBM撑靴与隧道围岩的作用进行分析。

1　仿真模型建立及计算参数选取

ABAQUS模型为60 m×60 m×60 m三维立方体模型，底面施加三向约束，侧面均施加法向约束，顶面不施加约束，且考虑掌子面到撑靴作用处的距离，预留部分隧道未开挖。为更加准确有效地模拟隧道开挖过程以及后续由于撑靴荷载导致的隧道围岩变形，本次计算将仿真模拟过程分为3个部分：初始地应力平衡、隧道开挖、施加撑靴荷载。开挖过程中，本模型将撑靴设置在隧道的中间位置。根据工程实际，隧道掘进长度为45 m，其余15 m为未开挖部分。岩土材料采用Mohr-Coulomb本构模型，为了更精确地划分单元，采用一阶四面体单元（C3D4），以便提高计算效率和计算精度。

TBM支撑系统由带有撑靴的水平支撑液压缸和竖直方向的扭矩液压缸组成，掘进时水平支撑液压缸使撑靴撑紧在洞壁上。根据工程实践经验，支撑力一般选取为推进力的2.6倍，最大单侧撑靴支撑力为其1/2［11］。本文所采用的是直径8.5 m开敞式TBM，由下式计算可得最大单侧撑靴支撑力为3.0×104kN，在考虑撑靴与隧道洞壁接触面积之后，单侧撑靴荷载为5.7 MPa。计算公式为

式中：Ft为TBM所需推进力，kN；Fμ为护盾摩擦力，kN；Fc为刀盘额定推力，kN；Fd为后配套系统拖动力，kN，可根据不同设计和质量进行估算；μ为摩擦系数；r为护盾半径，m；l为护盾长度，m；Pv为竖直载荷，kN/m2；Ph为水平载荷，kN/m2；G为TBM自重，kN；Fsc为单刀额定推力，kN；n为刀具数。

图1为仿真计算模型，各工况隧道围岩物理力学参数见表1。

图1　仿真计算模型

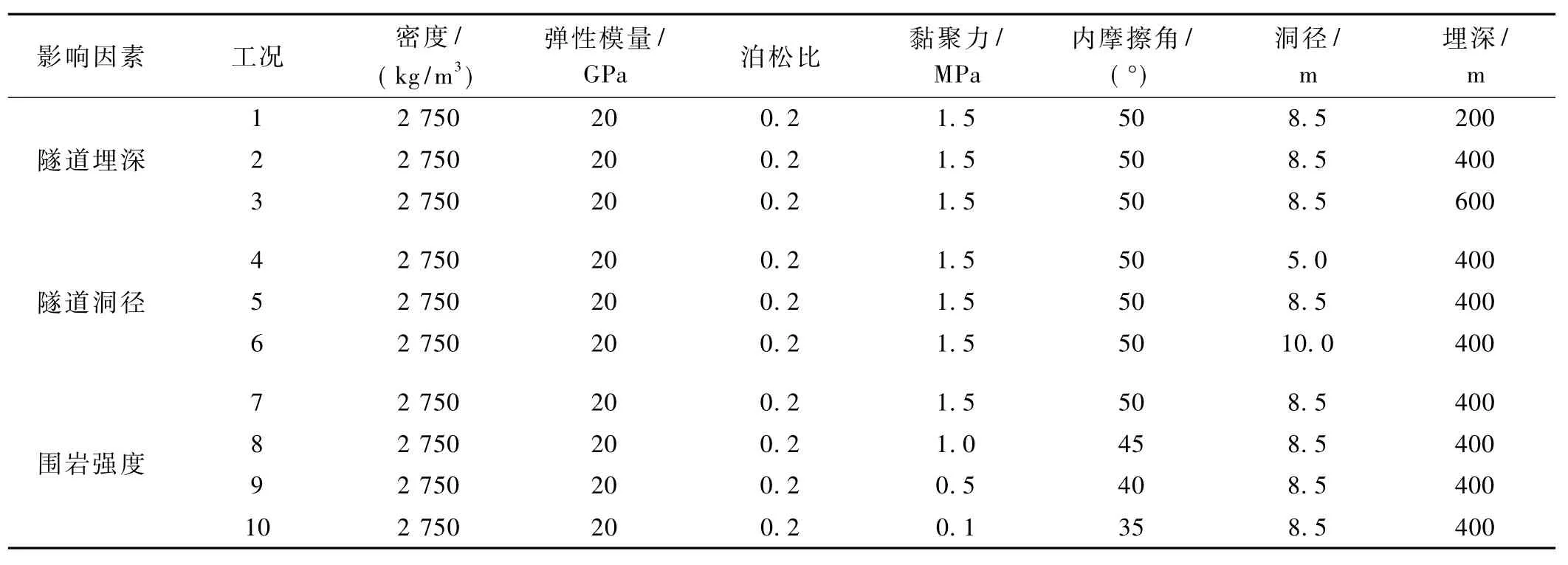
表1　各个工况隧道围岩物理力学参数

2　ABAQUS仿真计算结果分析

2.1隧道埋深的影响（工况1～工况3）

在围岩物理力学参数和洞径相同条件下，分别计算埋深为200，400，600 m 3种情况。

1）应力

不同埋深下隧道应力沿开挖方向分布曲线见图2。图中负值表示受压。由图2可知：不同埋深条件下，隧道的应力特征具有相似性，且径向应力、轴向应力均集中在距离洞口30 m处（撑靴所在位置）；随隧道埋深的增加，其上覆土层压力和围岩侧压力不断增大，隧道洞壁受撑靴作用所产生的径向压应力、轴向压应力均随之增大。

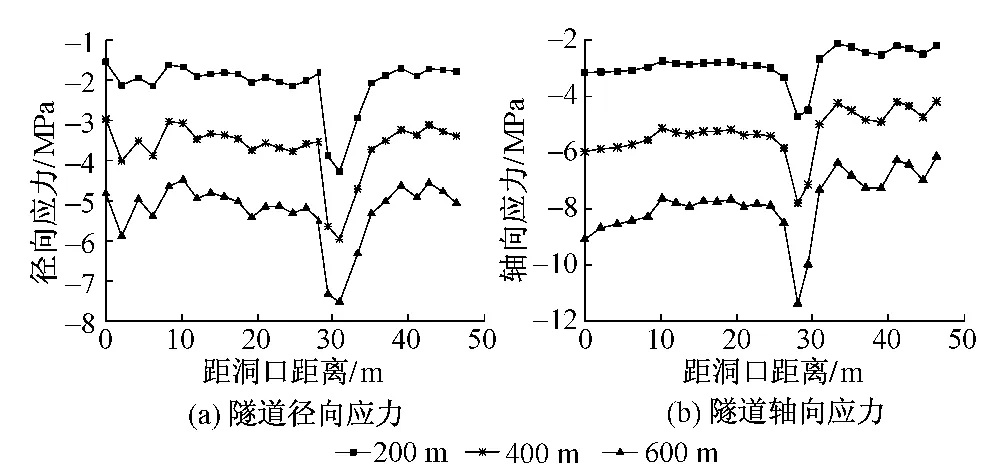
图2　不同埋深下隧道应力沿开挖方向分布曲线

2）位移

不同埋深下隧道位移沿开挖方向分布曲线见图3。由图3可以看出：径向位移随着隧道埋深的增加逐渐增大，集中在隧道撑靴所在位置；轴向位移的情况则较为复杂，即在洞壁与撑靴接触处，轴向位移随着隧道埋深的增加而减小。

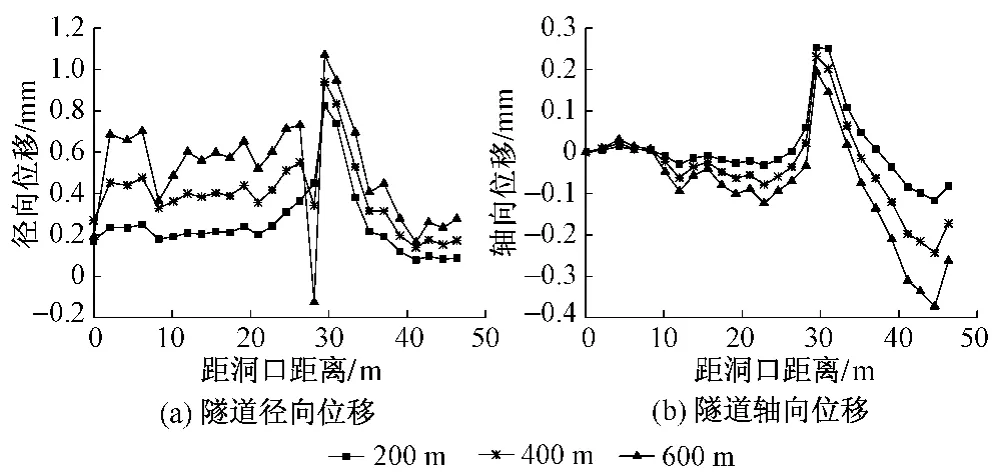
图3　不同埋深下隧道位移沿开挖方向分布曲线

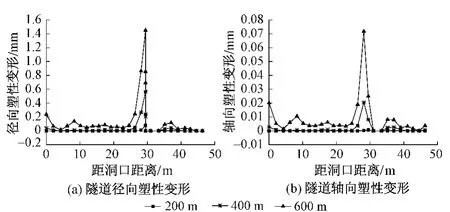
图4　不同埋深下隧道塑性变形沿开挖方向分布曲线

3）塑性变形

不同埋深下隧道塑性变形沿开挖方向分布曲线见图4。由图4可知：随着隧道埋深的增大，由于隧洞上覆土层的压力及侧面围压逐渐增大，在一定撑靴荷载作用下径向、轴向塑性变形程度逐渐增大，进而导致塑性变形影响范围扩大，不利于TBM的安全施工。

2.2隧道洞径的影响（工况4～工况6）

保持围岩物理力学参数和隧道埋深不变，模拟计算隧道洞径分别为5，8.5，10 m时围岩变形情况。

1）应力

不同洞径下隧道应力沿开挖方向分布曲线见图5。由图5可知：随隧道洞径的增大，径向应力和轴向应力影响范围和强度均逐渐增大，应力分布规律存在一致性。径向应力的增大趋势较轴向应力相对明显，但增幅较小。可以认为，隧道洞径的变化对于隧道结构强度无明显影响，在一定撑靴荷载作用下，其应力分布规律无明显差异。

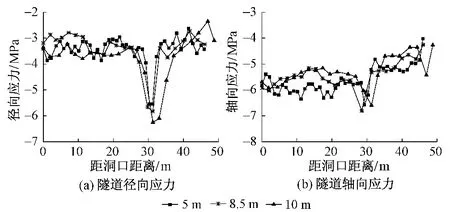
图5　不同洞径下隧道应力沿开挖方向分布曲线

2）位移

不同洞径下隧道位移沿开挖方向分布曲线见图6。由图6可知：在撑靴荷载作用下，隧道洞径增大时隧道径向、轴向位移均在逐渐增加，位移主要出现在洞壁两侧拱腰附近，以撑靴所在处位移最为显著。径向位移及轴向位移沿隧道开挖方向的分布曲线基本一致，大洞径隧道的位移较小洞径隧道有一定程度的增加，增幅不是很明显。隧道已开挖部分靠近洞口处变形较撑靴处分布相对平稳。

图6　不同洞径下隧道位移沿开挖方向分布曲线

3）塑性变形

不同洞径下隧道塑性变形沿开挖方向分布曲线见图7。由图7可知：随隧道洞径的增大，在撑靴荷载作用下隧道洞壁在径向和轴向的塑性区均逐渐增大，且关于隧道轴线对称；隧道洞径增加至10 m时径向、轴向塑性变形最大。不同洞径条件下径向塑性变形分布存在一致性，隧道径向塑性变形与隧道洞径间存在一定线性关系。轴向塑性变形分布受隧道洞径影响较为明显，较大洞径的隧道其轴向塑性变形的影响范围较小洞径隧道有所提升。10 m洞径隧道最大轴向塑性变形更靠近隧道洞口；这是因为撑靴需要提供TBM掘进时所需的推进力，隧道与撑靴接触处需要承担与推进方向相反的反力，较大洞径的隧道需要承担较大的反力，其最大轴向塑性变形会沿开挖反方向分布。2.3围岩强度的影响（工况7～工况10）

隧道围岩强度主要受到内摩擦角的影响，模型埋深为400 m，洞径为8.5 m。取4种典型工况进行计算，内摩擦角依次为50°，45°，40°，35°。

1）应力

不同围岩强度下隧道应力沿开挖方向分布曲线见图8。由图8可知：不同围岩强度条件下，由于撑靴作用导致的径向、轴向应力特征存在相似性；随着内摩擦角的减小（围岩强度的降低），在隧道与撑靴接触处径向应力有明显的增大趋势。由图8（b）还可以看出：在内摩擦角为35°时，围岩已经出现较明显的破坏。

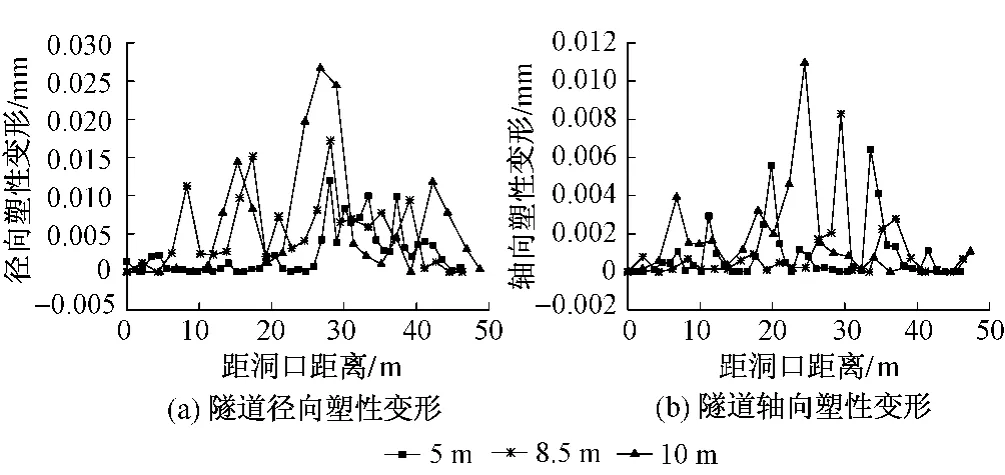
图7　不同洞径下隧道塑性变形沿开挖方向分布曲线

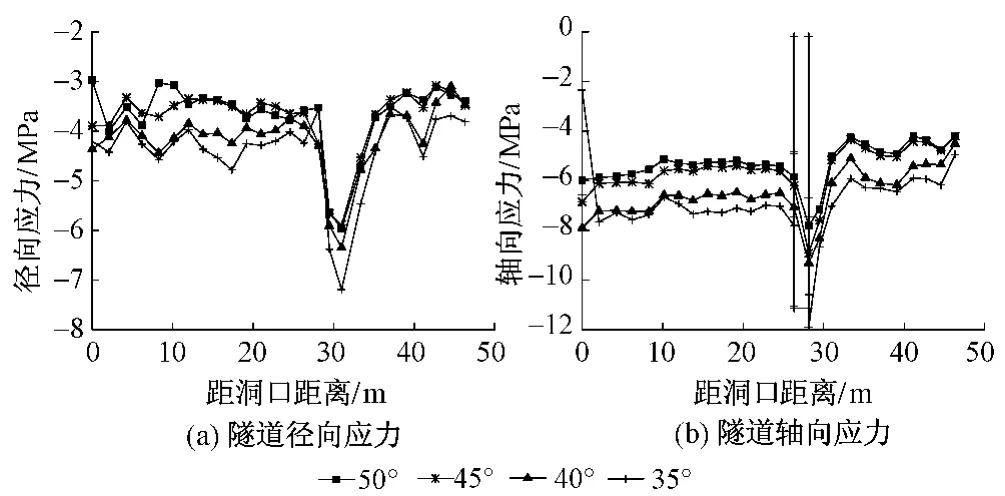
图8　不同围岩强度下隧道应力沿开挖方向分布曲线

2）位移

不同围岩强度下隧道位移沿开挖方向分布曲线见图9。由图9可知：经过全断面一次性开挖后，在撑靴荷载作用下隧道洞壁的位移主要出现在洞壁两侧拱腰；当内摩擦角按照50°，45°，40°，35°依次减小时，径向、轴向位移的影响程度、影响范围均呈增大趋势，最大变形均发生在撑靴与隧道洞壁的接触面处。从图9（b）还可以看出，由于围岩抗剪强度的减弱，当内摩擦角为35°时，在撑靴荷载作用下围岩已失稳破坏。

3）塑性变形

不同围岩强度下隧道塑性变形沿开挖方向分布曲线见图10。由图10可见：①随着内摩擦角依次减小，塑性变形区域逐渐增大，且最大塑性变形出现在TBM撑靴与隧道洞壁的接触面上。隧道径向变形主要受到撑靴压应力作用，内摩擦角的变化对于抗剪强度影响较大，从而对径向塑性变形影响也较大。②内摩擦角从50°变化到45°时，塑性区范围变化较小，影响程度也较小；随着抗剪强度的继续降低，当内摩擦角为40°时，塑性区范围明显增大，隧道已开挖部分的洞壁产生了明显的轴向塑性变形，说明隧道在撑靴荷载作用下此时已经濒临失稳破坏。③当内摩擦角减小至35°时，径向、轴向塑性变形的范围和程度均有显著的提升，从图10（b）还可以看出，隧道撑靴作用处发生了明显的失稳破坏。

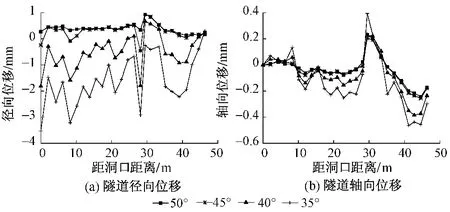
图9　不同围岩强度下隧道位移沿开挖方向分布曲线

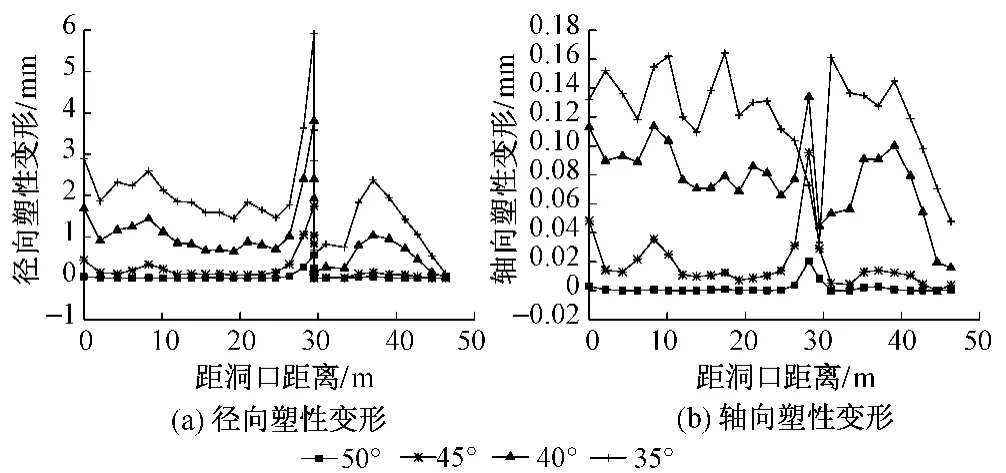
图10　不同围岩强度下隧道塑性变形沿开挖方向分布曲线

3　现场监测

根据辽西北供水工程掘进实测数据，绘制Ⅱ，Ⅲa和Ⅲb类围岩条件下TBM单侧撑靴支撑力沿掘进方向分布曲线，见图11。

由图11可知：在Ⅱ，Ⅲa和Ⅲb 3类围岩条件下单侧撑靴支撑力的波动较小；随着围岩强度降低，单侧撑靴支撑力平均值逐渐减小，这与模拟计算中考虑围岩强度因素所得趋势相同。在这3类常见围岩类型中，围岩单侧撑靴支撑力变化范围为24 900～25 900 kN，由此可推断出单侧撑靴径向应力为5.72～5.95 MPa，在考虑一定安全系数的情况下，与仿真计算结果较为一致。

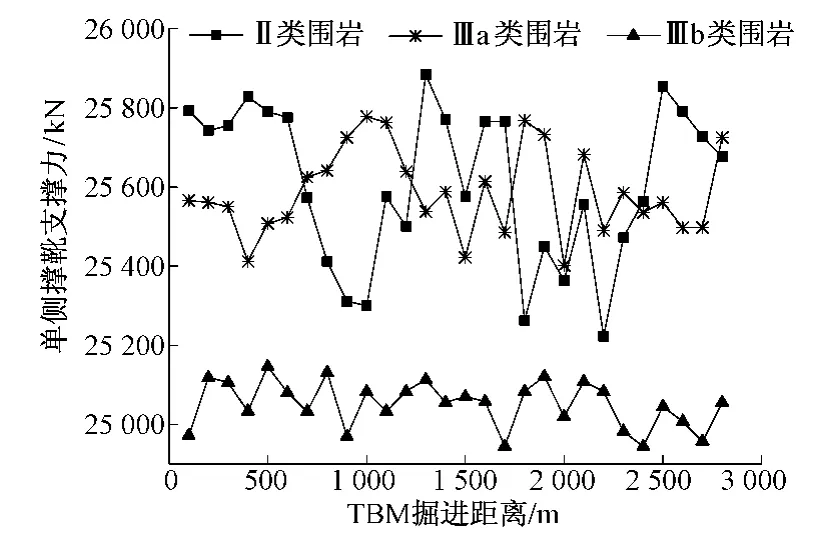
图11　Ⅱ，Ⅲa，Ⅲb 3类围岩单侧撑靴支撑力沿掘进方向分布曲线

4　结论

1）随着隧道埋深的增加，隧道围岩的稳定性逐渐增强；随着隧道洞径的增大，隧道围岩的稳定性逐渐降低，但变化幅度较小。

2）随着隧道围岩抗剪强度的降低，在撑靴荷载作用下隧道围岩的承载力逐渐降低，导致在TBM掘进过程中隧道围岩的稳定性逐渐降低。考虑安全系数的影响，建议实际工程中隧道围岩的内摩擦角不能小于45°，围岩抗剪强度较小的隧道，不宜使用TBM工法。

3）3种影响因素中，隧道围岩的稳定性对于围岩强度的变化最为敏感，其次是隧道埋深，最后为隧道洞径。因此，在隧道设计及施工方案选取时，将优先考虑隧道围岩强度和隧道埋深。在TBM掘进过程中，撑靴荷载应根据当前盾构机所处位置的围岩强度有所调整，在不引起围岩破坏的前提下提供最大的推进力。

4）依托实际工程，实测单侧撑靴支撑力值为24 900～25 900 kN，可推断出单侧撑靴径向应力为5.72～5.95 MPa，与仿真计算结果较为一致。

［1］杜士斌，揣连成.开敞式TBM的应用［M］.北京：中国水利水电出版社，2011.

［2］TANG Y，HUANG B H.Comparison of Gripper TBM and Double Shield TBM for Design and Selection［J］.Modern Tunnelling Technology，2009，46（2）：68-72.

［3］RAMONI M，ANAGNOSTOUG.The Interaction Between Shield，GroundandTunnelSupportinTBMTunnelling Through Squeezing Ground［J］.Rock Mechanics and RockEngineering，2011，44（1）：37-61.

［4］DELISIO A，ZHAO J，EINSTEIN H H.Analysis and Prediction of TBM Performance in Blocky Rock Conditions at the Lötschberg Base Tunnel［J］.Tunnelling and Underground Space Technology，2013，33：131-142.

［5］孟德鑫，谭忠盛，李涛.大直径土压平衡盾构掘进参数对比试验研究［J］.土木工程学报，2015，48（增1）：435-439.

［6］YAGIZ S.Utilizing Rock Mass Properties for Predicting TBM Performance in Hard Rock Condition［J］.Tunnelling and Underground Space Technology，2008，23（3）：326-339.

［7］TU Zhenguo，LU Yong.Evaluation of Typical Concrete Material Models Used in Hydrocodes for High Dynamic Response Simulations［J］.International Journal of Impact Engineering，2009，36（1）：132-146.

［8］张海彬.软岩隧道围岩的应力应变分析［J］.铁道建筑，2011（12）：72-74.

［9］娄霜.软岩公路隧道围岩变形影响因素探讨［J］.铁道建筑，2014（1）：49-52.

［10］庄茁，张帆，岑松，等.ABAQUS非线性有限元分析与实例［M］.北京：科学出版社，2005.

［11］张义同，高健，乔金丽，等.隧道盾构掘进土力学［M］.天津：天津大学出版社，2010.

（责任审编葛全红）

Research on Surrounding Rock Failure Mechanism due to Gripper Action of TBM（Tunnel Boring Machine）

LI Taifeng1，ZHENG Jie2，ZHANG Qianli3，LI Tao2
（1.China Academy of Railway Sciences，Beijing 100081，China；2.School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China；3.Railway Engineering Research Institute，China Academy of Railway Sciences，Beijing 100081，China）

Considering such three influence factors as the tunnel buried depth，tunnel diameter and surrounding rock strength，the interaction between T BM gripper and tunnel surrounding rocks，the surrounding rock deformation and failure laws were analyzed by using finite element analysis software ABAQUS，which were compared with the measured results.T he results show that the stability of surrounding rock increases with the tunnel buried depth increasing，the stability of surrounding rock gradually decreases and the changing amplitude is small with tunnel diameter increasing，the bearing capacity of tunnel surrounding rock decreases under the effect of gripper load with the shear strength decrease of the tunnel surrounding rock，which means that the internal friction angle of tunnel surrounding rock should not be less than 45 in practical engineering.Among the three influence factors，the tunnel surrounding rock stability is mostly sensitive to the change of surrounding rock strength，followed by the tunnel buried depth，and finally sensitive to the tunnel diameter.T he measured unilateral gripper support force is 24 900～25 900 kN in Northwest Liaoning water supply engineering and the unilateral gripper radial stress can be inferred as 5.72～5.95 M Pa，which is consistent with the simulation results.

T BM；Gripper；T unnel surrounding rock；Failure mode；T unnel construction；Numerical simulation

U455.4

A

10.3969/j.issn.1003-1995.2016.10.14

1003-1995（2016）10-0050-05

2016-07-10；

2016-07-25

国家自然科学基金高铁联合基金（U1434211）；铁道科学技术研究发展中心项目（J2014G004）；中国铁道科学研究院基金中日国际合作项目（2015YJ143）

李泰灃（1989—），男，博士研究生。