基于跨中位移影响线的箱梁损伤定位研究
张珂苑,蔺鹏臻
(兰州交通大学甘肃省道路桥梁与地下工程重点实验室,甘肃兰州730070)
基于跨中位移影响线的箱梁损伤定位研究
张珂苑,蔺鹏臻
(兰州交通大学甘肃省道路桥梁与地下工程重点实验室,甘肃兰州730070)
为了实现箱梁桥的损伤定位,利用梁式桥结构损伤必然影响弯曲刚度,则梁体跨中挠度影响线将不再以跨中为轴对称分布这一特点,提出了以桥梁损伤前后跨中挠度影响线三次差值为指标的损伤定位方法。对一座简支箱梁桥按照单一部位损伤和多部位同时损伤予以分析计算,在预设损伤部位均出现了损伤指标的明显突变,表明该方法对箱梁的单部位和多部位损伤定位具有较好的适用性。
桥梁;影响线;损伤定位;箱梁;跨中挠度
在我国的桥梁建设中,混凝土开裂是箱梁桥最普遍的病害形式之一,严重影响了结构的承载力和长期使用性能。最典型的裂缝是边跨现浇段和支座附近至1/4跨范围内的腹板斜裂缝[1-3]。在复杂的服役环境中,桥梁结构受到设计载荷的作用、材料的老化及各种突发性外在因素的影响而面临结构损伤累积、威胁到桥梁结构安全的问题。因此,研究了识别和检测结构损伤的理论和方法,建立了结构损伤识别系统,对结构进行在线监测和损伤识别研究,对结构的安全性、可靠性及结构的剩余寿命进行科学、准确地评估。
结构损伤识别是通过对结构的关键性能指标的测试和分析,判断结构是否受到损伤;如果结构受到损伤,检测损伤位置和损伤大小。根据使用的测量数据类型,现有的损伤识别技术可以分为2大类:①基于静态测量数据的结构损伤识别方法,以静态测量数据(如静态位移、静态应变等)对损伤进行识别[4];②基于动态测量数据的结构损伤识别方法,运用动态测量数据(如固有频率、模态振型、柔度等)对损伤进行识别。由于桥梁在施工时难免会有几何尺寸方面的误差,且材料(如混凝土)本身的弹性模量具有一定的不确定性,将直接导致未损伤的主梁的局部抗弯刚度并非为均匀的抗弯刚度。为此,陈记豪等[5]针对简支空心板桥建立了基于对称挠度差值影响线的损伤识别方法;刘纲、杜永峰等[5-6]对简支梁提出了利用某一点在损伤前后的位移(挠度)影响线变化来识别损伤的方法。但这些方法均没有专门考虑主梁抗弯刚度的不确定性,王艺霖等[8]基于跨中位移影响线差值指标,建立了考虑抗弯刚度不确定性的简支梁桥损伤定位方法。本文基于跨中位移影响线差值指标,研究简支箱梁的新型损伤定位方法。
1 损伤指标的建立
1.1移动荷载作用下跨中挠度的计算
主梁分析模型见图1。其中,l为跨度,EI为主梁完好状态的截面抗弯刚度。让一个集中荷载P在主梁上移动,用结构力学中的力法计算跨中位移[9]。
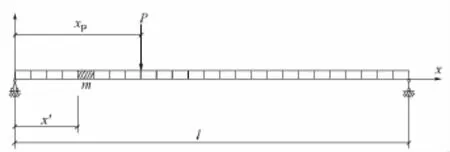
图1 主梁分析模型
当移动荷载P作用在xP位置时,根据式(1)计算梁端x位置截面的弯矩MP(x)。由力法原理可知,为求跨中挠度,需要通过式(2)计算单位力作用在跨中时距梁端x位置截面的弯矩
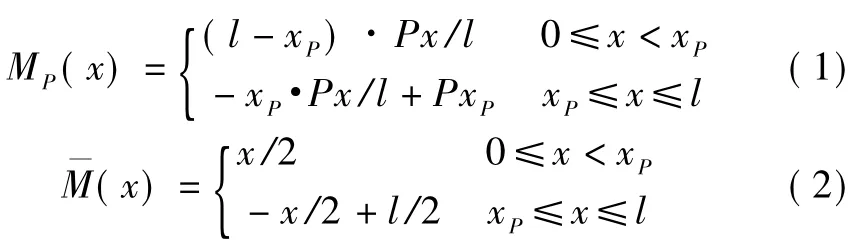
则跨中挠度为

1.2损伤定位指标的建立
假设由于某些因素导致梁体在距离左端x'处有一损伤,损伤使得该部位梁体抗弯刚度改变为αEI,其中α为损伤前后的抗弯刚度改变系数。将主梁沿纵向划分为长度均等于m的若干区间,则可用m表示损伤区域长度。将荷载作用在xP处时跨中位移的增量记为ΔxP,荷载作用在l-xP处时跨中位移的增量记为Δl-xP,二者的差值记为βxP。分别计算当荷载作用位置xP为x'-3m,x'-2m,x'-m,x',x'+m,x'+2m,x'+3m,x'+4m时的βxP,见式(4)~式(11)。
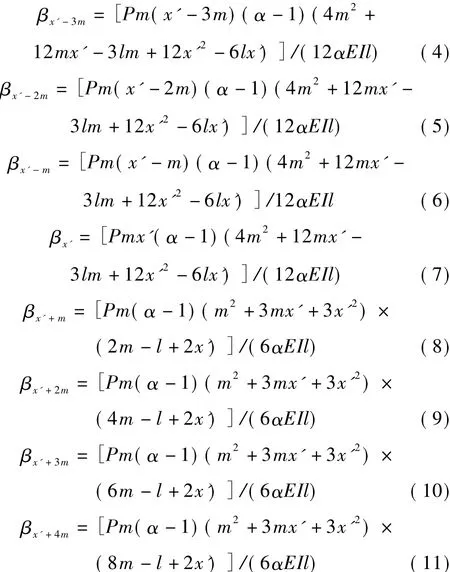
由式(4)~(11),可得到
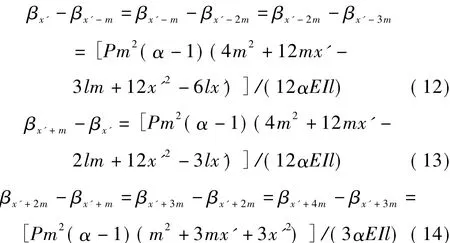
令γxP=βxP-βxP-m表示跨中位移影响线二次差值,则
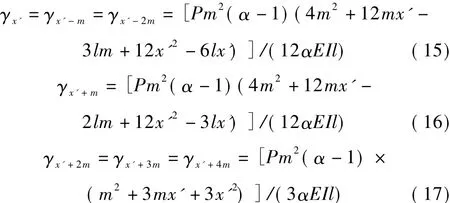

式(18)中,γW与γS分别表示梁体发生损伤前、后跨中位移影响线的二次差值,而Δγ为其三次差值。
对于未发生损伤的理想箱梁(α=1),由式(15)~(17)可以明显看出,γWxP≡0,所以Δγ=-γSxP;当主梁出现如图1所示的损伤后,γSxP发生突变,即Δγ发生突变,据此可以进行损伤定位。测量移动荷载作用下跨中的挠度时,需计算沿桥纵向不同位置的Δγx,如果距梁左端x处的Δγx发生突变,则损伤出现在区间[x-m,x]或其对称区间[l-x,l-x+m]。
2 箱梁中的损伤定位
一跨度为24 m的预应力混凝土简支箱梁桥[10],其截面尺寸如图2所示,理想弹性模量为34.5 GPa,箱梁承受的最不利荷载按照荷载组合原理等效为500 kN的集中力。
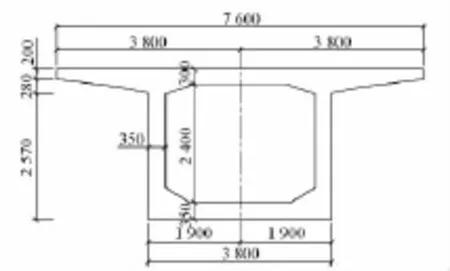
图2 截面尺寸(单位:mm)
假设桥梁在运营中,分别在箱梁顶板、底板和翼缘板出现了损伤,应用前述方法进行损伤定位。为了便于分析,箱梁不同部位的损伤采用沿截面横向宽度10 mm、深度50 mm的缺损来模拟。此外,考虑施工中由于截面误差、材料性能等造成梁体为非均匀刚度梁,假设本例分析中初始抗弯刚度在(0.98~1.02)EI随机分布。
2.1单一部位损伤
设梁体在使用中在[6.0 m,7.5 m]出现损伤,将主梁进行等长区间划分,每个区间长度为0.5 m,并结合杆系有限元法计算梁体位移,利用式(18)计算主梁损伤前后的Δγ。单一部位损伤Δγ分布曲线见图3,单一部位损伤的梁体损伤定位指标γ和Δγ见表1。
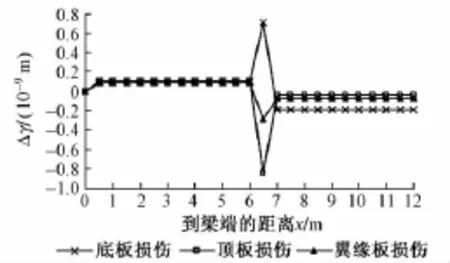
图3 单一部位损伤Δγ分布曲线
由表1和图3可以看出,当模拟顶板在[6.0 m,7.5 m]出现损伤时,Δγ在x=6.5 m处发生明显突变;对于底板和悬臂板模拟的损伤情况,Δγ在x=6.5 m处均出现明显突变,与事先设定的损伤位置完全对应,表明本文提出的损伤定位方法可完全识别出箱梁出现损伤的单个部位。

表1 单一部位损伤的梁体损伤定位指标γ和Δγm
2.2多个部位损伤
假设桥梁腹板出现4条不同裂缝:
①在x=1.1 m出现长0.3 m的纵向裂缝,记为A;
②在x=8.99 m出现长0.6 m的竖向裂缝,记为B;
③在x=17.3 m出现长1.2 m的纵向裂缝,记为C;
④在x=20.2 m出现长0.8 m的纵向裂缝,记为D。
基于本文理论计算得到多部位损伤的梁体损伤定位指标γ和Δγ见表2,多部位损伤指标Δγ分布曲线见图4。

表2 多部位损伤的梁体损伤定位指标γ和Δγm
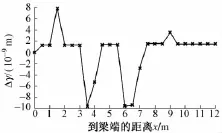
图4 多部位损伤指标Δγ分布曲线
由表2和图4可以看出,当模拟腹板的损伤出现在[1.0 m,1.5 m]时,Δγ在x=1.5 m处发生明显突变,对应事先设定的损伤位置A;Δγ在x=3.5 m,x= 4.0 m处发生明显突变,对应事先设定的损伤位置D;Δγ在x=6.0 m,x=6.5 m,x=7.0 m处发生突变,对应事先设定的损伤位置C;Δγ在x=9.0 m处发生突变,对应事先设定的损伤位置B。表明本文提出的损伤定位方法可以完全识别出箱梁出现损伤的多个部位。
3 结语
本文基于当简支梁某一段出现损伤后,梁体跨中挠度影响线将不再以跨中为轴对称分布这一特点,提出了以桥梁损伤前后跨中挠度影响线三次差值Δγ为指标的损伤定位方法。对于算例中,简支箱梁顶板、底板、悬臂板和腹板出现的不同损伤,通过计算损伤指标,发现在预设损伤部位均出现了损伤指标的明显突变。表明本方法对简支箱梁不同部位不同损伤的定位是准确的。
[1]丁勇,赵启林,马方圆,等.普通钢筋混凝土箱梁桥腹板竖向裂缝成因分析[J].工业建筑,2009,36(增1):919-922.
[2]巴力,王凯.大空心板梁跨中斜向裂缝的成因分析[J].铁道建筑,2015(11):18-20.
[3]职雨风,金滨.25 m小箱梁纵向裂缝分析及处治实例[J].广东公路交通,2002,76(增):194-195.
[4]TOMASZEWSKA A.Influence of Statistical Errors on Damage Detection Based on Structural Flexibility and Mode Shape Curvature[J].Computer and Structures,2010,88(3/4):154-164.
[5]陈记豪,赵顺波,姚继涛.基于对称挠度差值影响线的装配式简支空心板桥上部结构损伤识别[J].应用基础与工程科学学报,2014,22(2):283-293.
[6]刘纲,黄宗明,高建莉.基于损伤力影响线的静定梁损伤识别研究[J].湖南大学学报(自然科学版),2009,36(8):23-27.
[7]杜永峰,刘云帅,王晓琴.基于挠度差值影响线曲率的简支梁桥损伤识别[J].桥梁建设,2009(4):80-83.
[8]王艺霖,张鑫,安新梅.考虑抗弯刚度不确定性的简支梁桥损伤定位方法[J].中国公路学报,2015,28(3):82-87.
[9]李廉锟.结构力学[M].北京:高等教育出版社,2010.
[10]葛继平,王志强,彭大文,等.重复荷载下高铁24 m箱梁模型试验研究[J].武汉理工大学学报(交通工程与科学版),2013,37(4):741-744.
(责任审编郑冰)
Study on Box Girder Damage Location Based on Mid-span Displacement Influence Line
ZHANG Keyuan,LIN Pengzhen
(Key Laboratory of Road&Bridge and Underground Engineering Gansu Province,Lanzhou Jiaotong University,Lanzhou Gansu 730070,China)
In order to realize the damage location of the box girder bridge,a damage location method is proposed by using the characteristics of the girder bridges damage will inevitably affect the bending rigidity and the influence line of the mid-span deflection of the beam will no longer be symmetrical,which is the third difference of the influence line of the mid-span deflection before and after the bridge damage.A simple supported box girder bridge with single site and multiple sites damage condition were analyzed and calculated,then the damage index of the preset position was found to have a significant mutation.T he results show that the method is applicable for single site and multiple sites damage condition location of the box girder.
Bridge;Influence line;Damage location;Box girder;M id-span deflection
U441+.4
A
10.3969/j.issn.1003-1995.2016.10.02
1003-1995(2016)10-0006-04
2016-04-07;
2016-08-10
国家自然科学基金(51168030,51208242,51368031);甘肃省基础研究创新群体项目(1506RJIA029)
张珂苑(1991—),男,硕士研究生。
蔺鹏臻(1977—),男,教授,博士。

