基于LBI的二维复稀疏信号重建算法及应用研究

陈文峰　李少东　杨军

基于LBI的二维复稀疏信号重建算法及应用研究

陈文峰1李少东1杨军1

针对二维复稀疏信号重建时存在存储空间和计算复杂度增加的问题，本文提出了一种快速并行重建二维复稀疏信号的并行线性Bregman迭代（Parallel fast linearized Bregman iteration，PFLBI）算法.首先，构建了二维复稀疏信号的结构模型以及PFLBI算法基本迭代格式；其次，通过变步长方式提高迭代收敛速度，而每次迭代的步长则是通过估计中间变量的积累量突破收缩阈值需要的积累步数得到的；再次，对算法的性能指标进行了分析；最后，将该算法应用于逆合成孔径雷达（Inverse synthetic aperture radar，ISAR）成像.实验结果表明该算法在重建性能和速度上具有优势.

稀疏重建，二维信号处理，线性Bregman迭代，ISAR成像

引用格式陈文峰，李少东，杨军.基于LBI的二维复稀疏信号重建算法及应用研究.自动化学报，2016，42（4）:556−565

压缩感知（Compressive sensing，CS）理论作为一种新的信息获取手段，可基于信号结构的稀疏特性，在远低于奈奎斯特采样率的条件下，通过少数量测值实现对信号的精确重建［1−2］.由于能够有效缓解数据传输、存储和处理等方面的压力，相关的研究成果已涉及到图像［3］、通信［4］和雷达［5］等众多领域［6］.稀疏重建算法作为CS的核心内容之一，在一定程度上决定着能否将CS推向实用化［7］.传统的重建算法及相关研究大多是针对一维实信号［8］.然而在实际应用场景中，如阵列信号处理［9］、SAR［10−11］、ISAR（Inverse synthetic aperture radar）［12］和磁共振成像［13］等，待处理的往往是多维复数信号.目前对多维信号的处理主要有以下三种思路：1）将多维信号列向量化为一维；然后，利用一维重建算法进行处理，但是这种处理会使得感知矩阵规模急剧变大，显著增加计算复杂度.2）基于Kronecker积CS的思想［14］，其主要通过构建可分离感知算子降低算法的复杂度，实际上，利用小规模量测矩阵的Kronecker积对向量化的多维信号采样与利用小规模量测矩阵进行逐一采样是等价的.3）利用信号的联合结构特性进行多维处理.如文献［15］基于信号的块稀疏特征，将二维信号分为更小的块，然后利用块对角量测矩阵代替原始密集的量测矩阵进行采样，有效地降低了存储空间和计算复杂度.文献［16］基于二维信号的联合稀疏特征，利用同一个感知矩阵进行重建.但是当二维信号的稀疏结构具有任意性时，文献［15−16］所提算法的性能将变差.针对这一问题，文献［17］提出利用并行CS方案进行并行感知，并放松了对应的RIP（Restricted isometry property）条件.但文献［17］依然是对二维信号每列逐一重建，计算复杂度仍然较高，且该方法是在实数情况下讨论的，若在复信号情况下利用该方法，则需利用文献［10］的实数化方法，存储空间和计算复杂度会进一步增加.

而目前对复数信号重建主要有两种思路：1）将复信号的实部和虚部排列为实数化的信号后进行重建的思路［10］，该方法会增加信号以及感知矩阵的规模，造成存储空间和计算量增加.2）文献［8］采取迭代交替估计幅度和相位的思路进行复信号重建，但这种方法相当于两次优化过程，增加了计算复杂度.

为有效实现对二维复稀疏信号的快速重建，本文在线性Bregman迭代（Linearized Bregman iteration，LBI）的基础上，提出一种快速并行重建复稀疏信号的并行线性Bregman迭代（Parallel fast linearized Bregman iteration，PFLBI）算法.首先，构建了二维复稀疏信号的结构模型，详细分析了其信号结构特征；其次，从理论上推导了对二维复稀疏信号并行重建的并行Bregman迭代格式；然后，采用估计迭代步长的方法加快收敛过程以提高运算速度；最后，对PFLBI算法的收敛性，抗噪性和计算复杂度进行分析，仿真结果验证了理论分析的正确性.将PFLBI算法应用于ISAR成像中，仿真和实测数据成像结果都验证了算法的良好性能.

1　二维复稀疏信号模型

对于一个二维复稀疏信号，可以用矩阵形式来表示，假设二维复稀疏信号只有K个非零元素，此时称X是K稀疏的，X的稀疏程度可以用稀疏度向量来表示，其中Kd表示X的第d列的稀疏度，显然有图1给出了二维复稀疏信号的示意图.图1（a）给出了信号的幅度和位置，为更清晰地描述信号结构，图1（b）给出了信号的位置关系图，其中黑点表示该点为非零元素，白点表示该点为零元素.可以看出，当二维复稀疏信号具有任意稀疏结构时，其每一列的稀疏度和非零元素的位置都是任意的.而二维复稀疏信号的重建可表示为如下的数学问题：

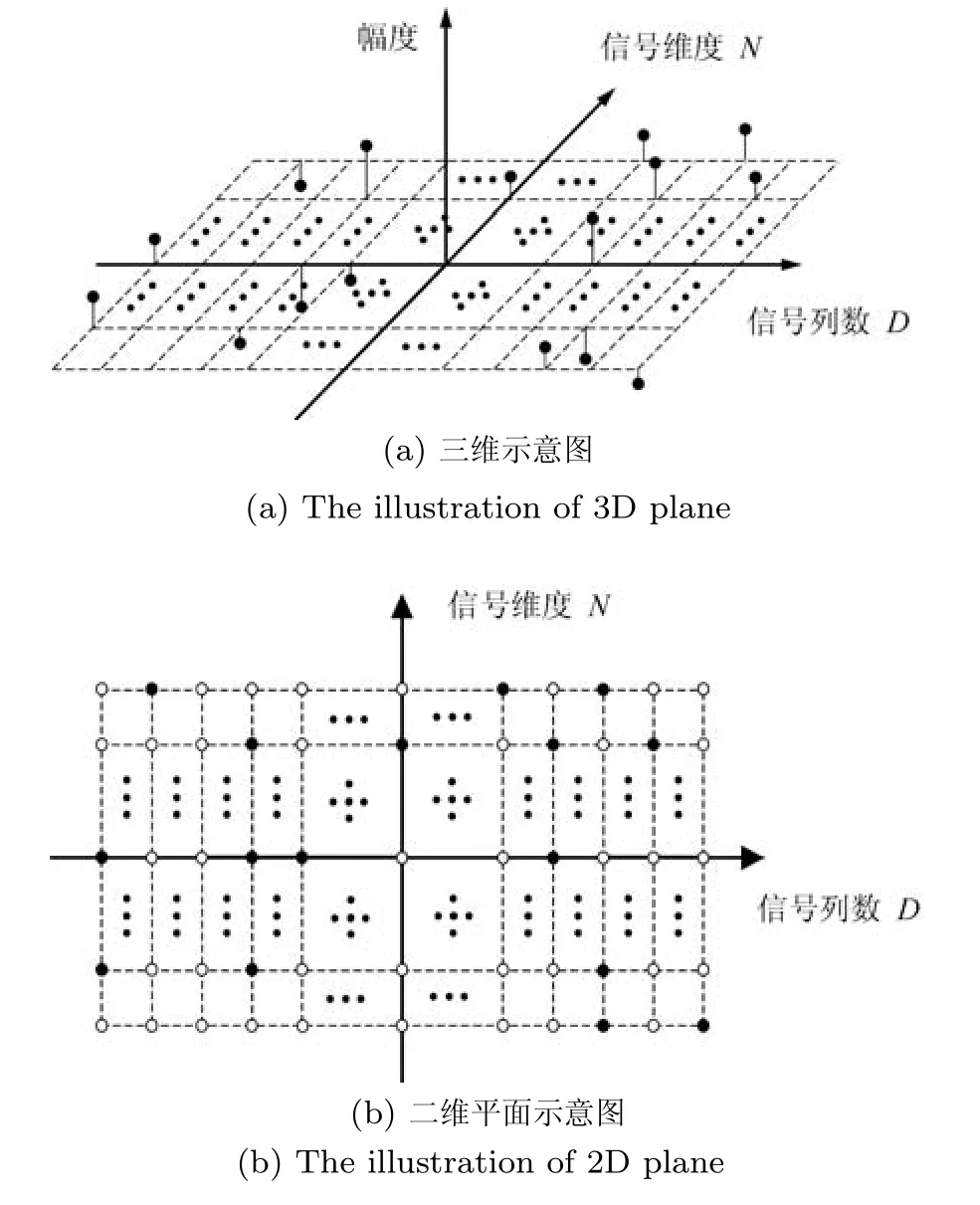
图1　任意稀疏结构二维复稀疏信号示意图Fig.1　The illustration of the 2D complex sparse signal with arbitrary sparse structure

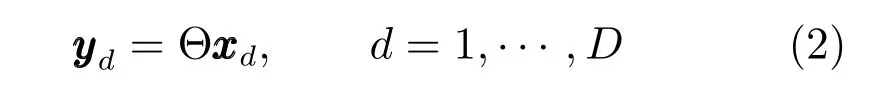
利用X的稀疏特性约束，求解式（1）的稀疏解问题可以描述为如下优化问题［18］：

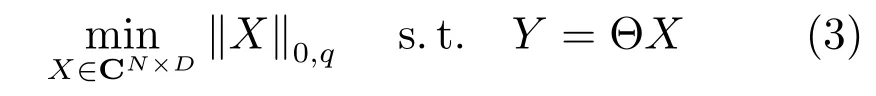
其中，‖X‖0，q=|supp（X）|，supp（X）为X的支撑集，即非零元素的个数.文献［17］证明了利用并行CS方案时，若感知矩阵Θ满足RIP条件，则二维复稀疏信号X能够从量测值Y中精确重建出来.由于式（3）是NP难的问题，在感知矩阵Θ满足RIP条件下，可将式（3）转化为以下凸优化问题［18］：

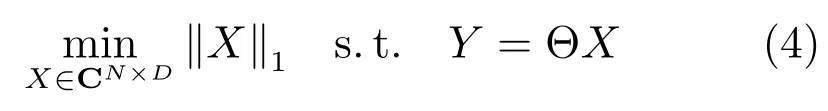
考虑到实际中存在噪声，为从含有噪声的量测值Y中恢复稀疏信号X，放松式（4）的约束项，利用正则化参数µ控制稀疏度和误差，转化为如下正则化形式［19］：

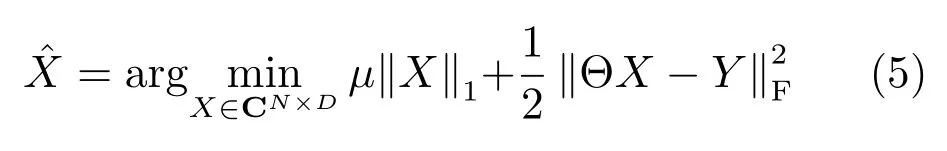
其中，‖·‖F表示矩阵的Frobenius范数，简称F范数，定义如下［20］：

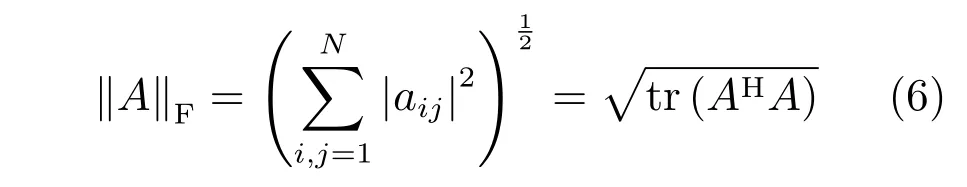
其中，tr（·）为矩阵的迹，即对角线元素之和.

2　PFLBI算法

为高效准确地求解式（5），本文提出PFLBI算法，该算法主要包括两个方面：1）构建PFLBI算法基本迭代格式，即将LBI拓展到二维复稀疏信号模型中，实现对二维复稀疏信号的并行重建；2）快速实现，即通过迭代步长的估计提高收敛速度，有效避免处理时造成的冗余计算，提高运算速度.下面进行具体介绍和分析.

2.1PFLBI算法基本迭代格式

PFLBI算法基本迭代格式的构建主要包括两部分：1）利用Bregman距离得到求解式（5）的Bregman迭代；2）将求解式（5）的Bregman迭代线性化，得到复矩阵形式的LBI.首先给出求解式（5）的PFLBI算法基本迭代格式，然后再对其证明.

采用LBI求解式（5）的最终迭代结果可表示为

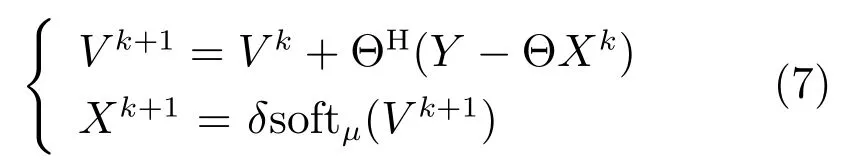
其中，Xk+1为迭代输出，Vk+1为中间变量，X0=V0=0，k=0，soft（·）为复矩阵条件的软阈值算子，定义如下：

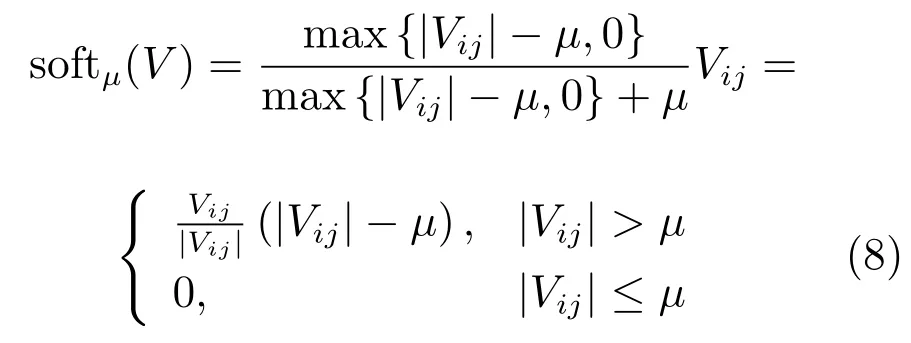
其中，Vij为复数矩阵V中第i行第j列的元素，|Vij|表示Vij的模.在对上式进行证明之前，首先给出两个定义：

1）不可微凸函数J（X）在点X 处的次微分定义为［21］

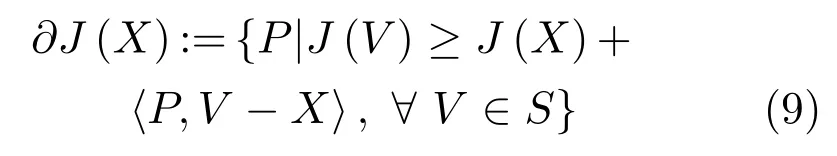
其中，S为J（X）的可行域，〈·，·〉为内积，矩阵P∈∂J（X）称为J（X）在点X处的次梯度.

2）凸函数J（X）上的点X和V的Bregman距离定义为［22］

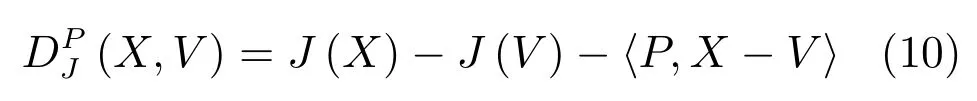
其中，向量P∈∂J（V）为凸函数J（X）在点V的次微分中的一个次梯度.

用J（X）的Bregman距离代替J（X），可得到式（5）对应的Bregman迭代形式：

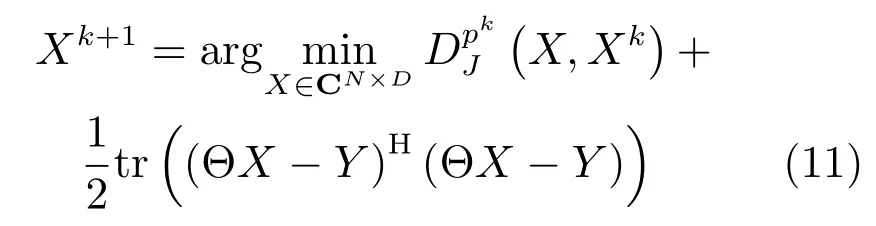
将J=µ||X||1带入式（12）并忽略常数项得：

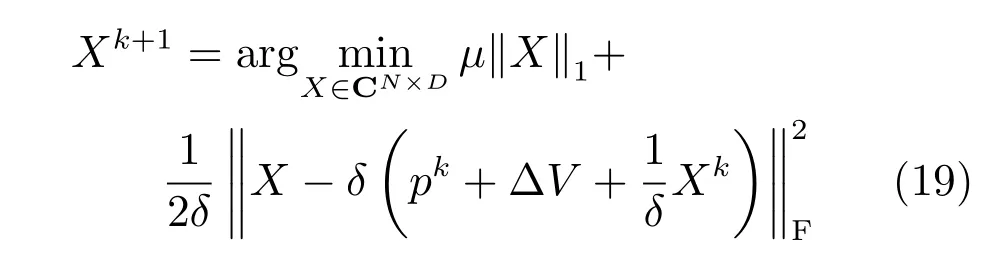
其中，∆V=ΘH¡Y−ΘXk¢.将ΘH（Y−ΘXk）=Vk+1−Vk及pk=Vk−Xk/δ代入式（19）得：

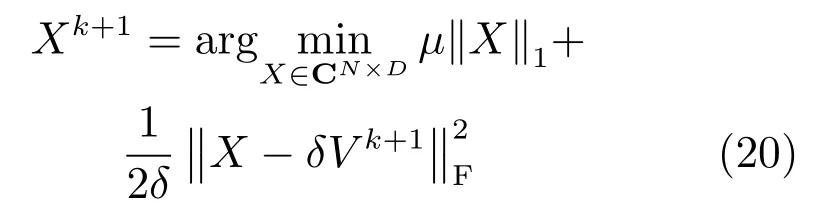
式（20）可用下式求解

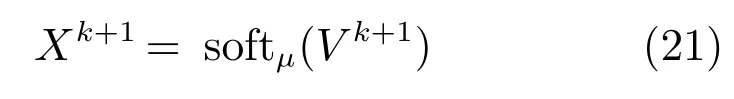
结合式（18）和（21）即得PFLBI算法基本迭代格式，此时完成了对式（7）的证明.

2.2快速实现

由于LBI存在停滞现象，式（7）也类似地存在停滞现象，因此需要研究消除这一现象的方法.文献［23］分析了LBI中停滞现象产生的原因：即一次或几次中间变量的积累量不足以突破收缩阈值，以至于这几次迭代时的输出保持不变.为解决这一问题，文献［23］提出利用改变迭代步长思想以消除实信号的停滞现象，取得了较好的效果，有效地加快了LBI的收敛速度.本文将该思想用于在二维复信号重建以消除停滞现象，下面进行具体分析.

消除停滞现象的重点在于估计V突破闭区间［−µ，µ］需要的步长，在停滞时间内，V的增量∆V=ΘH¡Y−ΘXk¢可认为是固定的.那么停滞期间的迭代过程可表示为

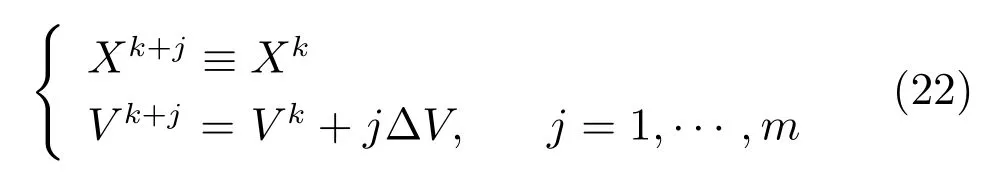
为计算停滞步长，首先对数据进行预处理.对Xk，Vk，Xk+j，Vk+j和∆V分别进行矩阵向量化处理，即

定义I0为零元素的索引集

非零元素的支撑集，此时式（22）可改写为如下分段形式：

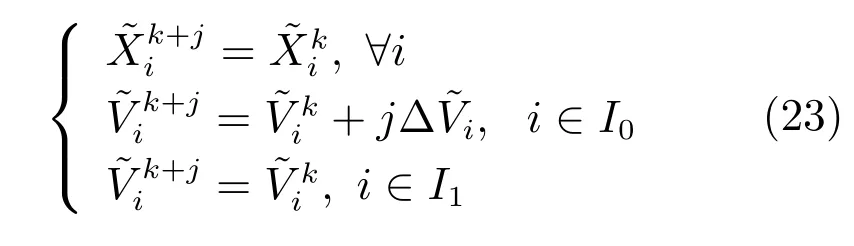
当且仅当I0中的元素突破闭区间［−µ，µ］的限制时，才会产生一个新的非零元素，从而消除停滞现象.当时，可以利用式（24）估计突破限制需要的积累步数，即

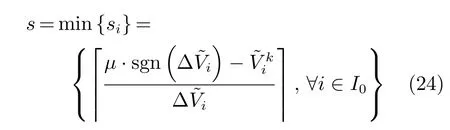
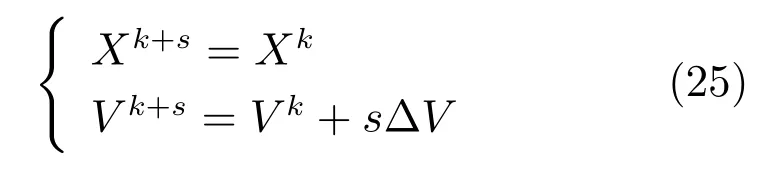
因此，当Xk在两步迭代保持不变时，认为其处于迭代停滞状态，此时可通过增加Vk的变化量以突破［−µ，µ］，从而使Xk加速到停滞的临界点，以此减少积累时间，加快算法运行速度.

注意到，本文方法能否较好地消除停滞现象主要取决于停滞状态Xk+s=Xk的判断是否准确.通常判断Xk+s=Xk是利用两者之差小于一个较小的常数ε，ε的取值不同会使算法的收敛速度不同：若ε的取值过小时，则两步迭代的Xk非常接近时，算法才会估计迭代步长，此时算法的收敛速度就较慢；若ε的取值较大时，则两步迭代的Xk相差较大时，算法便会估计迭代步长，此时算法的收敛速度就较快，但是，若ε的取值过大，算法会不收敛，因此选择ε时，需要考虑在算法收敛的条件下，选择较大的值，来获得较快的收敛速度，以减小停滞现象影响.

3　算法性能分析

3.1收敛性分析

对算法的收敛性进行分析时，主要分析式（7）是否收敛，因为PFLBI算法的输出序列是式（7）的子序列，因此，若式（7）收敛，则PFLBI算法必收敛.

下面对式（7）的收敛性进行分析.文献［24］给出了线性Bregman迭代的收敛性结论及证明，该文中的线性Bregman迭代可认为是式（7）的特殊情况，即实数向量形式，描述为式（26）.

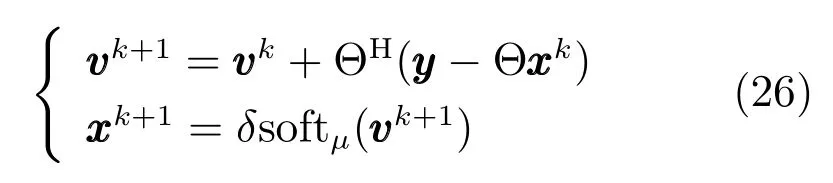
将文献［24］对于式（26）的收敛性定理描述为定理1.

实际中，为保证运算速度，算法处理时针对的是复数信号.在分析收敛性时，为方便分析，可利用式（31）将复数转化为实数进行分析［10］.

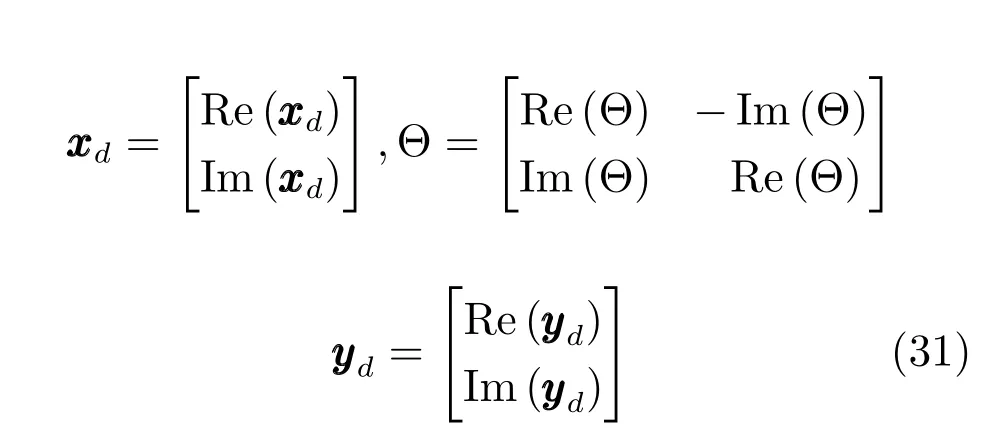
转化为实数后，式（30）满足定理1，显然式（29）也满足定理1，即式（7）满足定理1的收敛性结论，又有PFLBI算法的输出序列是式（7）的子序列，因此PFLBI算法也满足定理1的收敛性结论.

3.2抗噪性分析

PFLBI算法的主体部分是式（7），因此主要分析式（7）.为方便分析抗噪性能，类似于文献［25］，将式（7）写为等价的式（32）.

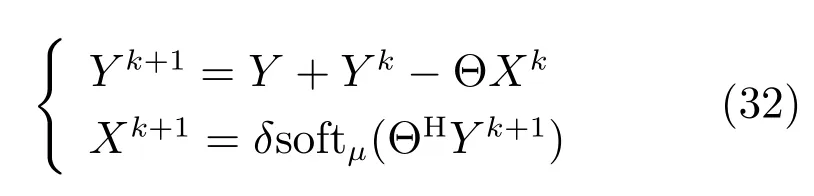
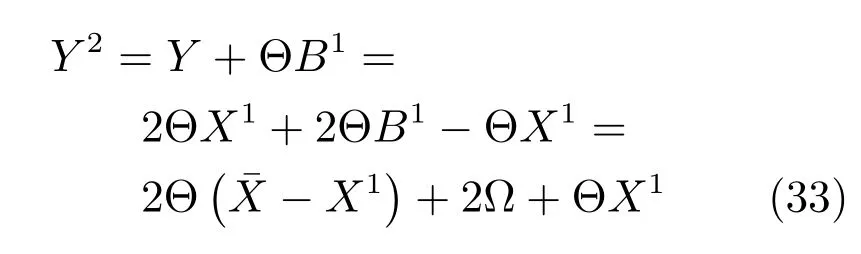
与第一次迭代含噪量测输入Y1相比，未恢复信号−X1变为两倍，同时Y2包含的噪声分量也变为两倍.由于第二次迭代新的含噪量测输入Y2可分解为Y2=ΘX2+ΘB2，利用Y2求解X2时，Y2中的信号成分不仅使X2继承了X1，而且重建了未恢复信号−X1的部分信息，因此X2比X1更逼近 ¯X.若已知噪声方差Σ2，则可以利用下式作为噪声条件下的停止准则：

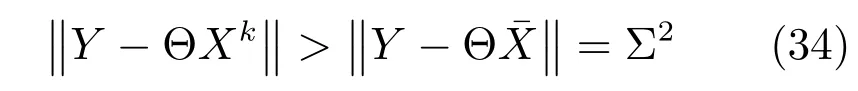
3.3计算复杂度分析

下面通过计算量分析比较算法的重建速度，以一次加法或乘法为计算量单位.

首先分析式（7）的计算量，一次迭代的计算量为O（D（4MN+2N）），假设经过L次循环得到最终解，那么式（7）的计算量为O（DL（4MN+2N））. PFLBI算法的计算量主要也是式（7）的迭代，主要是迭代次数不同，假设迭代L1次终止，那么总的计算量为O（DL1（4MN+2N））.由于PFLBI算法估计了停滞步长，因此有L1＜L.因此，PFLBI算法比式（7）的计算量更小，运算速度更快.

3.4并行性分析

本文算法不同于传统的逐列重建，而是整个矩阵同时重建，即多列同时重建.具有多个事件同时发生的思想，因而具有并行性.需要注意的是，本文算法的并行性和计算机领域利用多部计算机同时处理的并行计算并不完全相同，仅是思想相同.下面进行具体分析.

首先将LBI拓展到二维复稀疏信号模型中，实现直接对矩阵进行处理，以及对二维复稀疏信号的并行重建.此外，体现本文算法并行性关键的一点是处理矩阵时，将原始对向量收缩的软阈值算子改进为可直接对矩阵进行收缩的软阈值算子，因而本文算法能够并行重建二维复稀疏信号.

4　仿真与实验

这里首先通过仿真对算法的性能进行验证分析，然后通过仿真数据及实测数据的ISAR成像进一步验证算法的性能与优势，仿真中，采用计算机语言为Matlab语言，计算机主要参数如下：处理器为Intel酷睿E7500，主频为2.93GHz，内存为2GB.

4.1算法性能验证与分析

仿真1.可行性验证

本仿真主要验证本文算法对于已有复数模型算法的有效性，因此重点与文献［8，10］中的方法进行比较.针对一般的复数信号，其中a幅度服从正态分布a～N（0，1），θ服从均匀分布的长度为256，稀疏度为10，感知矩阵是128×256的随机高斯矩阵，算法停止准则为，最大迭代次数为5000，相对重建误差定义为仿真结果如图2所示.

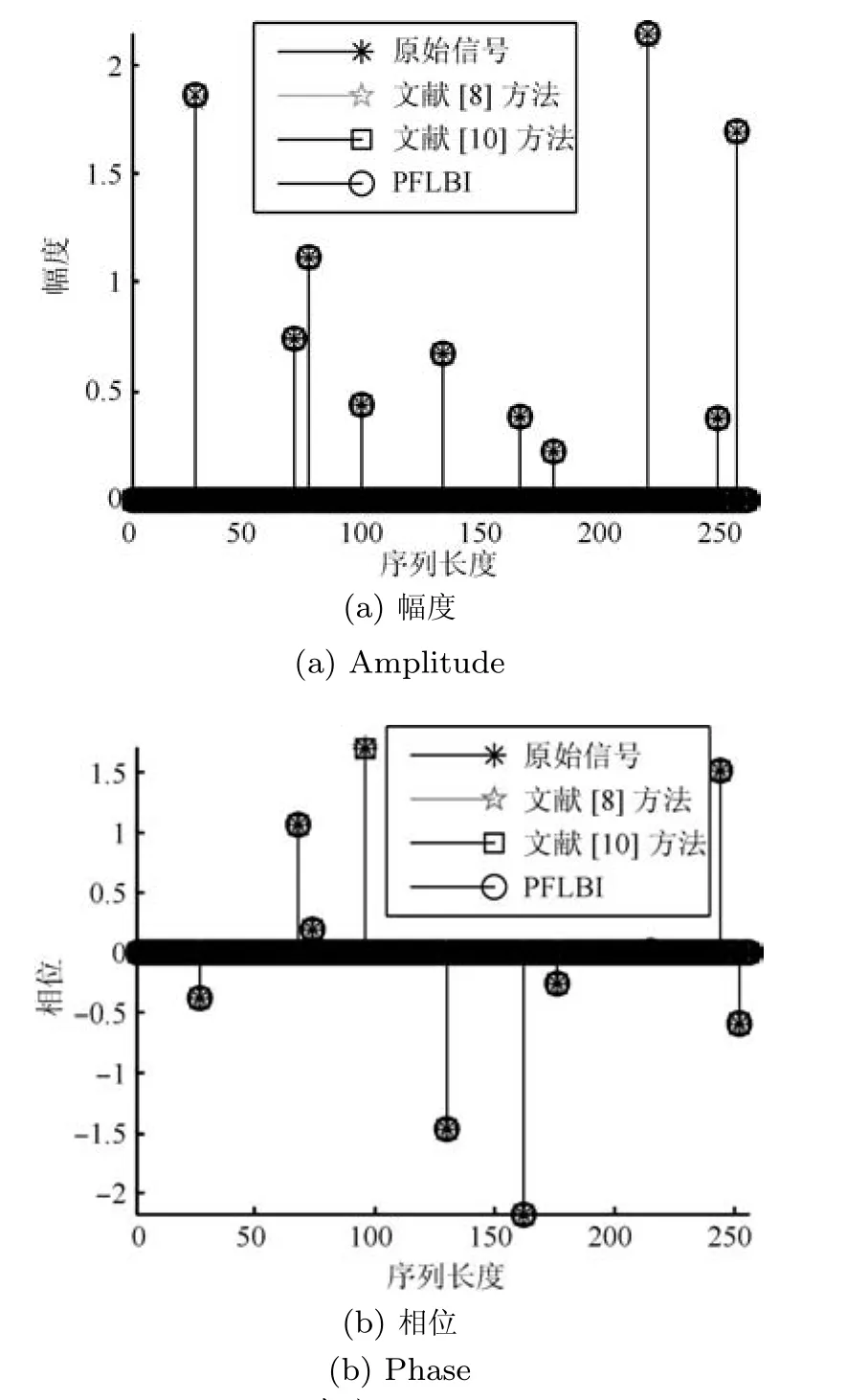
图2　本文算法重建结果Fig.2　Reconstruction results by the proposed algorithm

从图2中可以看出，文献［8，10］的方法以及本文的PFLBI算法都能够有效地重建稀疏复信号的幅度和相位，验证了本文算法的有效性.

仿真2.收敛性验证

下面通过仿真对算法的收敛性进行验证，仿真参数与仿真1相同，相对重建误差的对数和迭代次数的变化关系如图3所示.

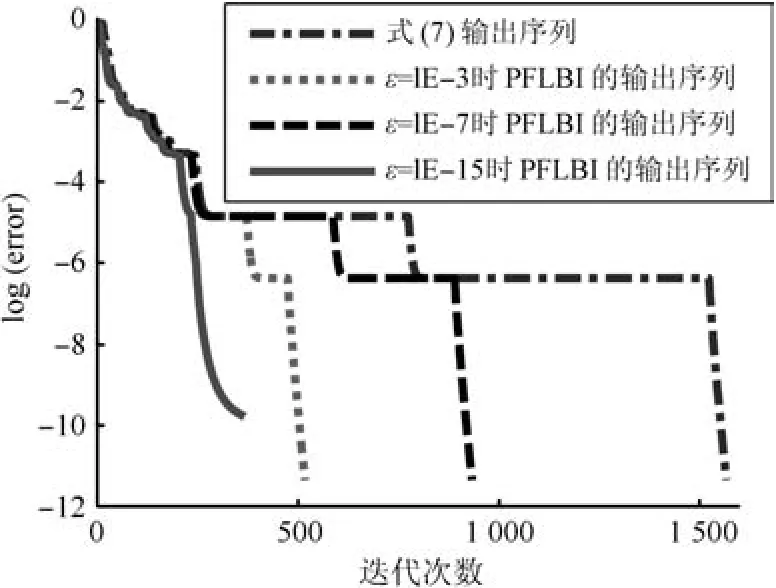
图3　算法收敛性验证Fig.3　Verification of convergence of the proposed algorithm

从图3可以看出，式（7）和PFLBI算法的输出序列的相对重建误差随迭代次数的增加，最终减小到设定的停止门限，验证了PFLBI算法收敛性.同时可看出式（7）存在停滞现象，PFLBI算法通过估计迭代步长的方法有效地消除了停滞，减少了迭代次数，加快了收敛速度，体现出PFLBI算法的优势.此外，可以看出，算法的收敛速度与ε的取值有关，ε值越小，则收敛速度越慢；ε值越大，则收敛速度越快；但ε的取值过大时，则算法不收敛，仿真验证了理论分析的正确性.

仿真3.抗噪性验证

本仿真主要考察PFLBI算法的重建精度对信噪比的敏感度，并与文献［8］和文献［10］的方法进行比较，仿真参数与仿真1相同，噪声取复高斯白噪声，信噪比的取值范围是［0dB～35dB］，步长为5，Monte Carlo仿真100次.图4为相对重建误差与信噪比的关系.

由图4可以看出，在较低的信噪比下，3种算法的相对重建误差都比较大，都不能准确地重建出原始信号；随着信噪比的增大，3种算法的相对重建误差都越来越小.可以看出本文PFLBI算法优于文献［8，10］的方法.

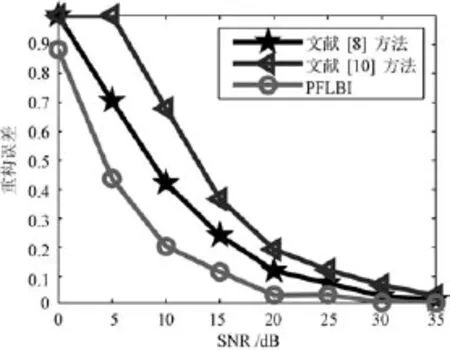
图4　相对重建误差与信噪比的关系Fig.4　Relationship between relative reconstruction error and SNR

仿真4.运算时间比较

本仿真主要验证PFLBI算法的速度优势，仿真时与文献［8，10］的方法进行比较.PFLBI算法停止准则及最大迭代次数与仿真1相同.信号序列长度的取值范围是［256～1024］，步长为128，Monte Carlo仿真100次.不同算法的运算时间关系如图5所示.

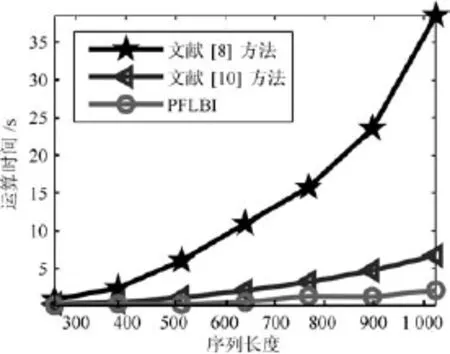
图5　不同算法运算时间比较Fig.5　Comparison of CPU time of different algorithms

由图5可知，随着信号序列长度的增加，算法的运算时间都有所增加，由于文献［8］的方法需要两次优化，因此时间最长；文献［10］的方法需要将复数实数化，增加了信号序列和感知矩阵的维度；而本文算法能够直接处理复数信号，所用时间较短，验证了本文算法的优势.

4.2仿真数据ISAR成像

为更好地验证本文算法的优势，将所提算法应用于ISAR方位向成像.CS ISAR成像的核心思想是利用ISAR图像的稀疏性，从少量回波中得到高分辨率甚至超分辨率图像.文献［12，26−27］已经对CS ISAR成像做了较为全面深入的研究，本文算法应用于ISAR方位向成像的基础与这些文献相同，这里就不再赘述.文献［12，26−27］中的CS ISAR方位向成像是逐个距离单元进行重建，而本文方法是利用所提的PFLBI算法对所有距离单元同时重建，达到并行处理的目的，在保证成像质量的同时提高了成像效率.仿真参数设置如下：发射信号为线性调频（Linear frequency modulation，LFM）信号，载频为10GHz，发射脉冲时宽10µs，信号带宽为400MHz，采样频率为800MHz，脉冲重复频率为200Hz.目标为34个散射点飞机模型，假设飞机匀速飞行，速度为300m/s，观测距离门参考位置50km，脉冲回波数为256个.目标模型及脉压后结果如图6所示.

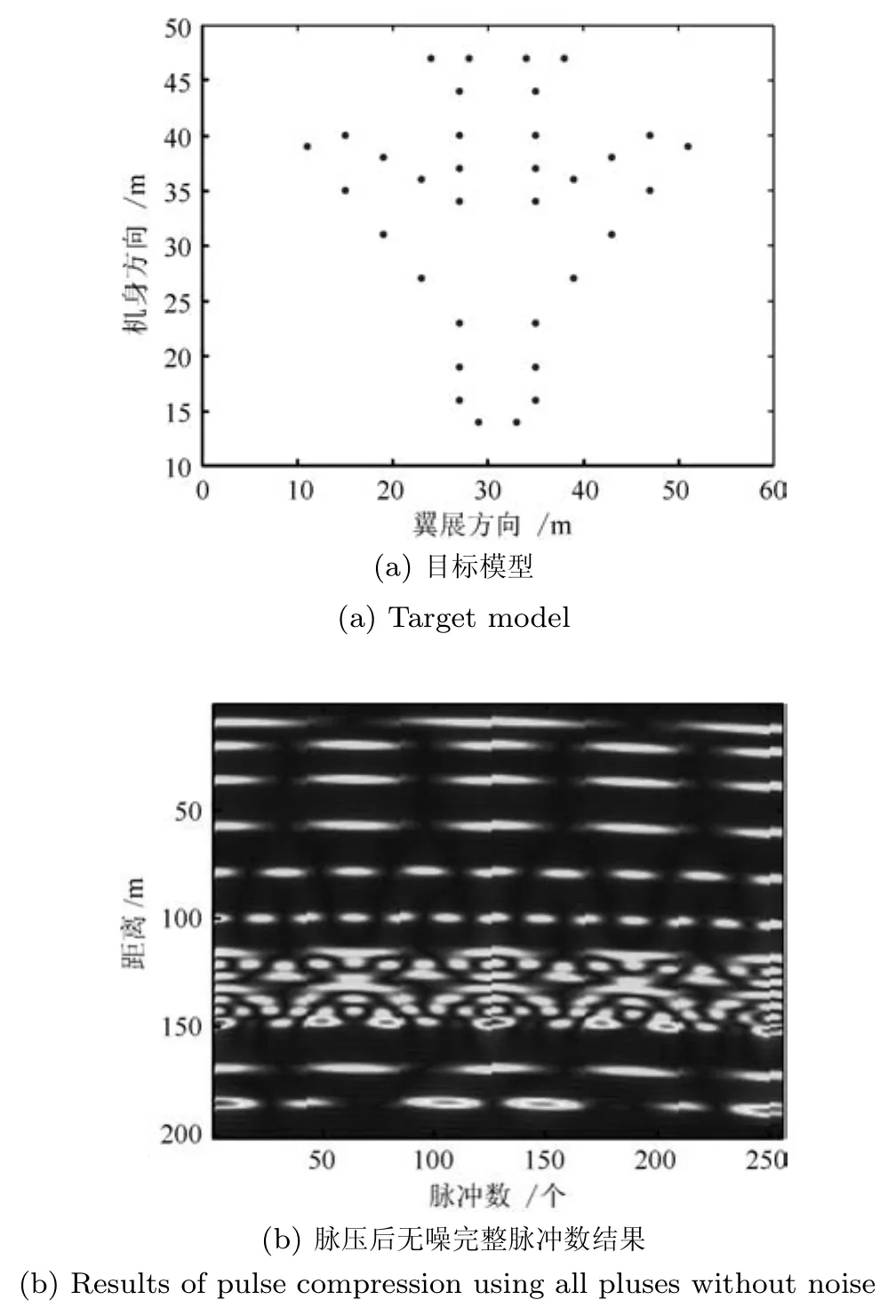
图6　目标模型及脉压后结果Fig.6　Target model and results of pulse compression

为验证三种算法在不同信噪比下的有效性与成像效果，分别与RD（Range dopler）算法和OMP（Orthogonal matching pursuit）算法成像结果比较. PFLBI算法中δ=1/（2‖ΘΘT‖），µ=300/δ.图7（a）图7（c）分别为RD算法、OMP算法和PFLBI算法在不同信噪比条件下得到的ISAR成像仿真结果.

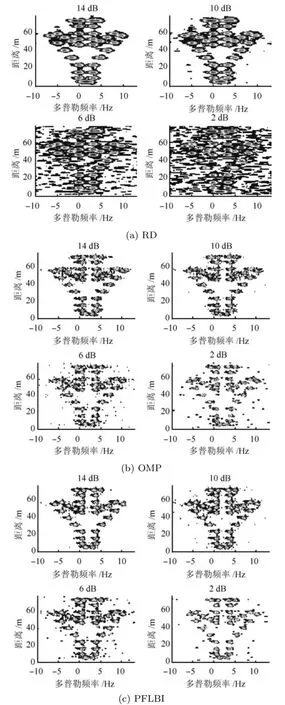
图7　不同信噪比仿真数据成像结果Fig.7　Images under different SNR by simulation data

由图7可知，相比RD算法，基于CS理论的三种重建算法得到的ISAR图像分辨率更高，副瓣更低.随着信噪比的降低，三种算法的成像质量都有所下降：RD算法成像结果在低性噪比下受噪声影响严重；由于利用噪声方差作为算法的停止准则，OMP算法和PFLBI算法受信噪比影响较小；对比图像可知，PFLBI算法比OMP算法的成像结果副瓣更低，虚假散射点更少，验证了本文算法在不同信噪比下的良好成像性能.

4.3实测数据ISAR成像

为更好地验证算法性能，下面利用实测数据进行实验验证.部分雷达参数如下：雷达发射信号为LFM信号，带宽为100MHz，工作频段为S波段，脉冲重复频率为400Hz，回波脉冲数为1570个.实测数据不同信噪比的成像比较.PFLBI算法中δ=1/（2‖ΘΘT‖），µ=300/δ.其中图8为实测数据脉压后信噪比分别为14dB、10dB、6dB、2dB的结果，图9（a）～（c）分别为RD算法、OMP算法和PFLBI算法在不同信噪比条件下得到的实测数据ISAR成像结果.

从图9可以看出，随着信噪比的降低，三种算法的成像质量都有所下降，都会出现丢失部分散射点信息及出现虚假散射点的情况：其中RD算法分辨率较低，成像结果受噪声影响严重，低信噪比时出现大量虚假散射点；OMP算法和PFLBI算法提高了分辨率，降低了副瓣，受信噪比影响较小，但PFLBI算法成像结果优于OMP算法，副瓣更低，虚假散射点更少.实测数据进一步验证了PFLBI算法在不同信噪比下的良好成像性能.

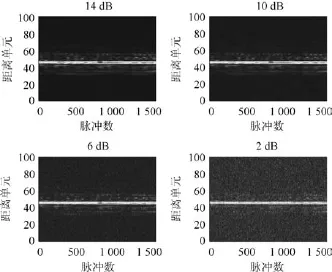
图8　实测数据脉压后不同信噪比回波结果Fig.8　Results of pulse compression under different SNR by real data

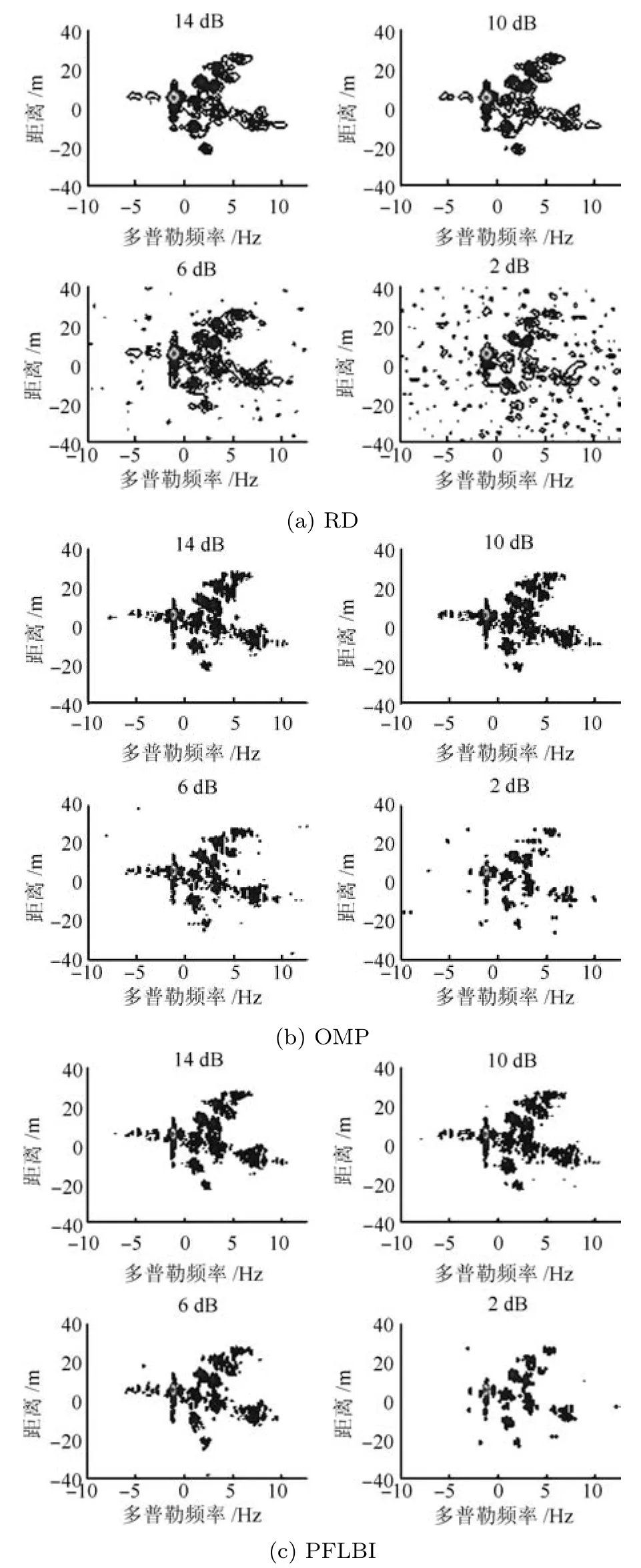
图9　不同信噪比实测数据成像结果Fig.9　Images under different SNR by real data

5　结论

本文针对重建二维复信号时，出现的存储空间和计算复杂度增加的问题，首先，构建了任意稀疏结构的二维复稀疏信号模型.然后，基于LBI构建了PFLBI算法基本迭代格式，同时利用估计迭代步长的方法加快了收敛过程，提出了PFLBI算法.理论和仿真分析表明，PFLBI算法具有良好的收敛性、抗噪性和重建二维复稀疏信号时速度的优势，同时，PFLBI算法能够有效消除停滞现象，提高运算效率.最后，将PFLBI算法应用于ISAR成像，不同信噪比的仿真及实测数据成像结果验证了PFLBI算法的良好性能.

References

1 Donoho D L.Compressed sensing.IEEE Transactions on Information Theory，2006，52（4）:1289−1306

2 Jing Nan，Bi Wei-Hong，Hu Zheng-Ping，Wang Lin.A survey on dynamic compressed sensing.Acta Automatica Sinica，2015，41（1）:22−37（荆楠，毕卫红，胡正平，王林.动态压缩感知综述.自动化学报，2015，41（1）:22−37）

3 Shen Yan-Fei，Li Jin-Tao，Zhu Zhen-Min，Zhang Yong-Dong，Dai Feng.Image reconstruction algorithm of compressed sensing based on nonlocal similarity model.Acta Automatica Sinica，2015，41（2）:261−272（沈燕飞，李锦涛，朱珍民，张勇东，代锋.基于非局部相似模型的压缩感知图像恢复算法.自动化学报，2015，41（2）:261−272）

4 Zhang Wen-Lin，Niu Tong，Qu Dan，Li Bi-Cheng，Pei Xi-Long.Feature space nonlinear manifold based acoustic model for speech recognition.Acta Automatica Sinica，2015，41（5）:1024−1033（张文林，牛铜，屈丹，李弼程，裴喜龙.基于声学特征空间非线性流形结构的语音识别声学模型.自动化学报，2015，41（5）: 1024−1033）

5 Fang Biao，Huang Gao-Ming，Gao Jun.A multichannel blind compressed sensing framework for linear frequency modulated wideband radar signals.Acta Automatica Sinica，2015，41（3）:591−600（方标，黄高明，高俊.LFM宽带雷达信号的多通道盲压缩感知模型研究.自动化学报，2015，41（3）:591−600）

6 Massa A，Rocca P，Oliveri G.Compressive sensing in electromagnetics-a review.IEEE Antennas and Propagation Magazine，2015，57（1）:224−238

7 Wu Zheng-Hua，Wang Qiang，Liu Jie，Sun Ming-Jian，Shen Yi.Compressive sensing theory based on edge expander graphs.Acta Automatica Sinica，2014，40（12）:2824−2835（伍政华，王强，刘劼，孙明建，沈毅.基于边膨胀图的压缩感知理论.自动化学报，2014，40（12）:2824−2835）

8 Yu S W，Khwaja A S，Ma J W.Compressed sensing of complex-valued data.Signal Processing，2011，92（7）: 357−362

9 He Z Q，Shi Z P，Huang L，So H C.Underdetermined DOA estimation for wideband signals using robust sparse covariance fitting.IEEE Signal Processing Letters，2015，22（4）: 435−439

10 Ender J H G.On compressive sensing applied to radar.Signal Processing，2010，90（5）:1402−1414

11 Dong X，Zhang Y H.A novel compressive sensing algorithm for SAR imaging.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2014，7（2）: 708−720

12 Xu G，Xing M D，Bao Z.High-resolution inverse synthetic aperture radar imaging of manoeuvring targets with sparse aperture.Electronics Letters，2015，51（3）:287−289

13 Yang Y，Liu F，Xu W L，Crozier S.Compressed sensing MRI via two-stage reconstruction.IEEE Transactions on biomedical engineering，2015，62（1）:110−118

14 Duarte M F，Baraniuk R G.Kronecker compressive sensing.IEEE Transactions on Image Processing，2012，21（2）: 494−504

15 Gan L.Block compressed sensing of natural images.In:Proceedings of the 15th International Conference on Digital Signal Processing.Cardiff，UK:IEEE，2007.403−406

16 Cotter S F，Rao B D，Engan K，Kreutz-Delgado K.Sparse solutions to linear inverse problems with multiple measurement vectors.IEEE Transactions on Signal Processing，2005，53（7）:2477−2488

17 Hao F，Vorobyov S A，Hai J，Taheri O.Permutation meets parallel compressed sensing:how to relax restricted isometry property for 2D sparse signals.IEEE Transactions on Signal Processing，2014，62（1）:196−210

18 Duarte M F，Eldar Y C.Structured compressed sensing: from theory to applications.IEEE Transactions on Signal Processing，2011，59（9）:4053−4085

19 Tropp J A.Algorithms for simultaneous sparse approximation.Part II:convex relaxation.Signal Processing，2006，86（3）:589−602

20 Zhang Xian-Da.Matrix Analysis and Applications（2nd edition）.Beijing:Tsinghua University Press，2013.32−35（张贤达.矩阵分析与应用.第2版.北京:清华大学出版社，2013. 32−35）

21 Erdogan A T，Kizilkale C.Fast and low complexity blind equalization via subgradient projections.IEEE Transactions on Signal Processing，2005，53（7）:2513−2524

22 Bregman L M.The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming.USSR Computational Mathematics and Mathematical Physics，1967，7（3）: 200−217

23 Osher S，Mao Y，Dong B，Yin W.Fast linearized Bregman iteration for compressive sensing and sparse denoising.Communications in Mathematical Sciences，2011，8（1）:93−111

24 Cai J F，Osher S，Shen Z W.Linearized Bregman iterations for frame-based image deblurring.SIAM Journal on Imaging Sciences，2009，2（1）:226−252

25 Yin W，Osher S，Goldfarb D，Darbon J.Bregman iterative algorithms for e1-minimization with applications to compressed sensing.SIAM Journal on Imaging Sciences，2008，1（1）:143−168

26 Li Shao-Dong，Yang Jun，Ma Xiao-Yan.High resolution ISAR imaging algorithm based on compressive sensing. Journal on Communications，2013，34（9）:150−157（李少东，杨军，马晓岩.基于压缩感知的ISAR高分辨成像算法.通信学报，2013，34（9）:150−157）

27 Zhang S H，Zhang W，Zong Z L，Tian Z，Yeo T S.Highresolution bistatic ISAR imaging based on two-dimensional compressed sensing.IEEE Transactions on Antennas and Propagation，2015，63（5）:2098−2111

陈文峰空军预警学院博士研究生. 2014年获得空军预警学院硕士学位.主要研究方向为压缩感知，逆合成孔径雷达成像.本文通信作者.E-mail:chenwf925@163.com

（CHEN Wen-FengPh.D.candidate at the Air Force Early Warning Academy.He received his master degree from Air Force Early Warning Academy in 2014.His research interest covers compressed sensing and inverse synthetic aperture radar imaging.Corresponding author of this paper.）

李少东空军预警学院博士研究生. 2012年获得空军预警学院硕士学位.主要研究方向为压缩感知，逆合成孔径雷达成像.E-mail:liying198798@126.com

（LI Shao-DongPh.D.candidate at the Air Force Early Warning Academy. He received his master degree from Air Force Early Warning Academy in 2012. His research interest covers compressed sensing and inverse synthetic aperture radar imaging.）

杨 军空军预警学院副教授.2003年获得空军工程大学博士学位.主要研究方向为雷达系统，雷达成像，压缩感知.E-mail:yangjem@126.com

（YANG JunAssociate professor at the Air Force Early Warning Academy. He received his Ph.D.degree from Air Force Engineering University in 2003. His research interest covers radar system，radar imaging，and compressed sensing.）

2D Complex Sparse Reconstruction Algorithm with LBI and Its Application

CHEN Wen-Feng1LI Shao-Dong1YANG Jun1

A parallel fast linearized Bregman iteration（PFLBI）algorithm is proposed to solve the problem of large storage and complex computation in the reconstruction of 2D sparse signal.The PFLBI algorithm can efficiently reconstruct 2D sparse signal in a parallel way.Firstly，the matrix form of linearized Bregman iteration（LBI）is constructed.Secondly，the convergence speed is improved by estimating the number of the steps for intermediate variables to cross the shrinkage threshold.Thirdly，the performance of the proposed algorithm is analyzed.Finally，PFLBI is applied to inverse synthetic aperture radar（ISAR）imaging.Experimental results show that the proposed algorithm can improve the performance and the speed of reconstruction.

Sparse reconstruction，2D signal processing，linearized Bregman iteration（LBI），inverse synthetic aperture radar（ISAR）imaging

Manuscript December 25，2014；accepted December 7，2015

10.16383/j.aas.2016.c140897

Chen Wen-Feng，Li Shao-Dong，Yang Jun.2D complex sparse reconstruction algorithm with LBI and its application.Acta Automatica Sinica，2016，42（4）:556−565

2014-12-25录用日期2015-12-07

国家自然科学基金（61179014）资助

Supported by National Natural Science Foundation of China（61179014）

本文责任编委张长水

Recommended by Associate Editor ZHANG Chang-Shui

1.空军预警学院武汉430019

1.Air Force Early Warning Academy，Wuhan 430019