基于压缩感知的自适应加权匹配追踪算法

余　翔，郑寒冰，曾银强

(重庆邮电大学 通信与信息工程学院，重庆 400065)



基于压缩感知的自适应加权匹配追踪算法

余翔，郑寒冰，曾银强

(重庆邮电大学 通信与信息工程学院，重庆 400065)

压缩感知(compressed sensing, CS)技术通过减少发射导频数来提高频谱的利用率。将CS技术应用于导频辅助的稀疏度未知的正交频分复用(orthogonal frequency division multiplexing, OFDM)信道估计中，提出一种自适应加权匹配追踪(CS-based adaptive weighting & matching pursuit, AWMP)算法。该算法使用自适应加权、匹配追踪的方法估计信道时域脉冲响应，按照估计信噪比和匹配原则，利用多次迭代进行自适应加权和寻找最佳稀疏度，实现未知信道稀疏度与信噪比的情况下，准确估计信道信息。仿真验证表明，与传统的信道估计算法相比，采用基于AWMP的信道估计方法，能够利用较少的导频信息获得更低的误码率和均方误差。

压缩感知；信道估计；稀疏性；信噪比；自适应加权；匹配追踪

0　引　言

正交频分复用(orthogonal frequency division multiplexing，OFDM)系统[1]中，信道估计的准确性对系统性能有较大的影响，但传统信道估计未充分考虑无线信道的固有稀疏性，导致估计性能不够理想[2-3]。研究表明，实际的无线信道大都存在稀疏性，合理利用这种稀疏性，就能通过较少的导频获得更多、更准确的有用信息。将压缩感知(compressed sensing, CS)技术[4]应用于OFDM信道估计的研究受到广泛重视。文献[5-7]提出CS技术可充分利用信道的稀疏特性，使用有限导频信息就能有效地恢复稀疏信道的脉冲响应。由于实际系统中很难满足现有CS算法需要已知信道稀疏度的要求，因此，寻找新的稀疏度自适应重构算法，在减少导频数目的同时可在稀疏度未知的情况下准确恢复信号，实现稀疏信道的准确估计尤为重要。

针对基于压缩感知的信道估计，文献[8]中的基追踪算法，通过线性规划的方法多次迭代进行精确重构，但其计算复杂度高。文献[9-10]采用匹配追踪(matching pursuit, MP)算法和正交匹配追踪(orthogonal matching pursuit, OMP)算法，其中应用最为广泛的OMP算法[10-12]是一种贪婪迭代算法，其每次迭代只抽取一个原子进行计算，运算速度较慢。文献[13]提出了多原子抽取方法，运算速度快，但抽取步长难以确定，易造成误判和多抽取，甚至会在原子抽取与残差增加之间造成恶性循环。

针对传统算法存在的问题，本文提出一种自适应加权匹配追踪(adaptive weighting & matching pursuit， AWMP)算法，通过估计信噪比后，自适应计算残差使之逐步逼近门限，同时采用均衡后的导频信噪比修正估计信噪比，使信道参数更准确，达到降低误码性能和信道估计均方误差的目的。

1　压缩感知信道估计模型与重构算法

1.1压缩感知信道估计模型

为方便计算，目前信道模型大多采用离散时域表示，设离散时域信道的冲击响应为h(n)，其数学表达式为[14]

(1)

(1)式中：hl是第l个抽头的复增益；L为信道最大长度。稀疏信道中，h=[h0,h1,…,hL-1]T中大部分hl值趋于零，只有极少个非零元素。设发送端的OFDM子载波数为N，x(n)为发送的时域信息序列，频域为X，z(n)为零均值的加性高斯白噪声，频域为Z，接收端接收的时域信号为y，频域表示为

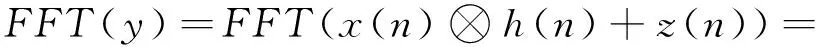
XFh+Z

(2)

(2)式中，F为N×N维傅里叶矩阵前M行L列构成的部分傅里叶矩阵。

(3)

频域中，假设插入P个子载波用于导频符号的传输，记为XP，其插入位置为p=[p1,p2,…,pP]，pu∈[0,N-1]，收端接收到的导频信息为

Yp=XpFph+Zp

(4)

(4)式中：Xp=diag[X(p1),…,X(pP)]；根据(3)式知，Fp∈CP×L表示F中对应前P×L维矩阵；h=[h(1),…,h(L)]T；Yp=[Y(p1),…,Y(pP)]T；Zp=[Zp(1),…,Zp(P)]表示均值为0，方差为σ2IP的加性高斯白噪声。因此，(4)式估计h是一种典型的系数信号重构问题，可完全采用基于压缩感知的重构算法。

1.2重构算法

重构算法的关键是从低维的接收信号中高概率地重构出高维的原信号，即根据已知的变换基和观测矩阵，计算出满足(4)式的最优系数解。

目前，重构算法主要有如下几种。

1)凸优化算法。如基追踪(basis pursuit，BP)算法，利用凸优化的思想，转换为一个线性规划的问题。

2)组合算法。对信号采样的恢复通过分组测试快速实现。典型的有链式追踪。

3)贪婪迭代算法。代表算法有匹配类追踪算法，如OMP算法等。这种算法的总体思想是通过每次迭代时选择一个与信号最匹配的解来逐步逼近原始信号，同时计算信号残差，之后再从残差中寻求最优解，当迭代次数达到预定值，停止迭代。其迭代条件与信道的稀疏度有关，但信道的稀疏特性会导致采用该信道模型进行信号重构时，信道冲击响应中包含噪声，效果不够理想。

2　自适应加权匹配追踪算法

传统匹配类算法对信道稀疏度和噪声比较敏感，稀疏度决定算法的迭代停止条件，信噪比影响着信道估计的准确性。而实际中信噪比和稀疏度的不可预知性限制了压缩感知信道估计的现实应用。为此，本文提出通过估计信噪比和自适应加权匹配追踪算法改善压缩感知信道估计性能。

2.1信噪比的初始估计

在未知信道稀疏度与信噪比情况下，估计信噪比更容易，因此，可采用先估计一个初始值，然后在每次迭代中加权更新信噪比估计值的方法。

由于OFDM符号的保护带内不发送任何数据，可将其收到的信号看作噪声。通常，噪声功率在一段频带内呈较均匀的分布，可将其平均功率作为信噪比的初始估计值Zw。记保护带内接收信号序列为Xz=(Xz(1),…,Xz(Nw))，则噪声功率为

(5)

由以上得知，OFDM符号有N个子载波，收到的信号为X=(X(1),…,X(N))，其功率值为

(6)

则

(7)

2.2自适应加权匹配追踪方法

传统的匹配追踪算法中引入了加权降噪的思想，即在最小二乘算法(least square，LS)估计中引入加权因子，利用残差对大小加权因子进行惩罚、扩充，减少异常样本。但研究发现加权效果并非适用于所有信噪比环境。

图1是基于加权与非加权的传统OMP算法的信道估计均方误差(mean squared error, MSE)对比图。根据图1，只有在小于10 dB的低信噪比时，加权性能才更好，否则，性能降低。

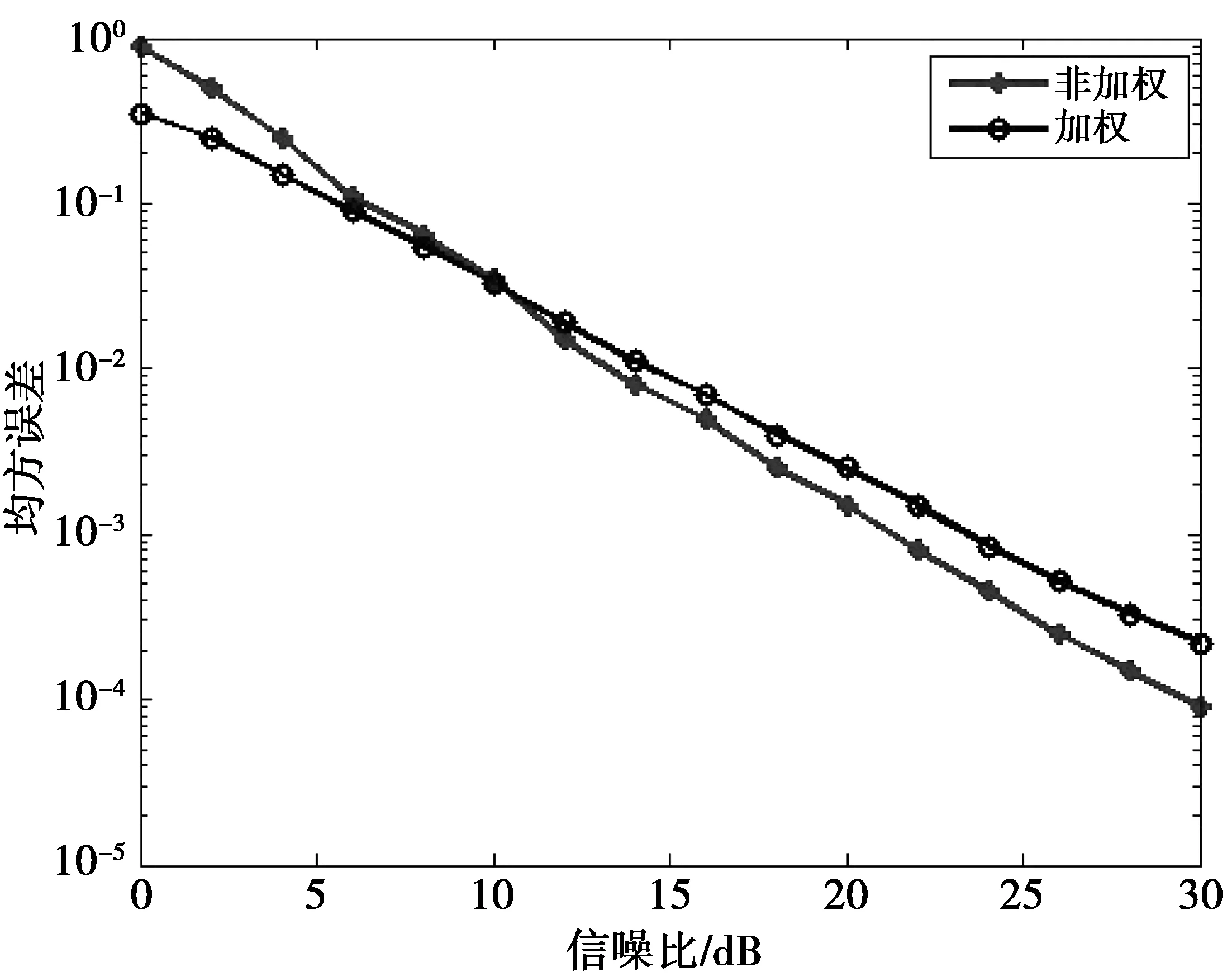
图1　加权与非加权均方误差对比图Fig.1　MSE under weighted and non-weighted

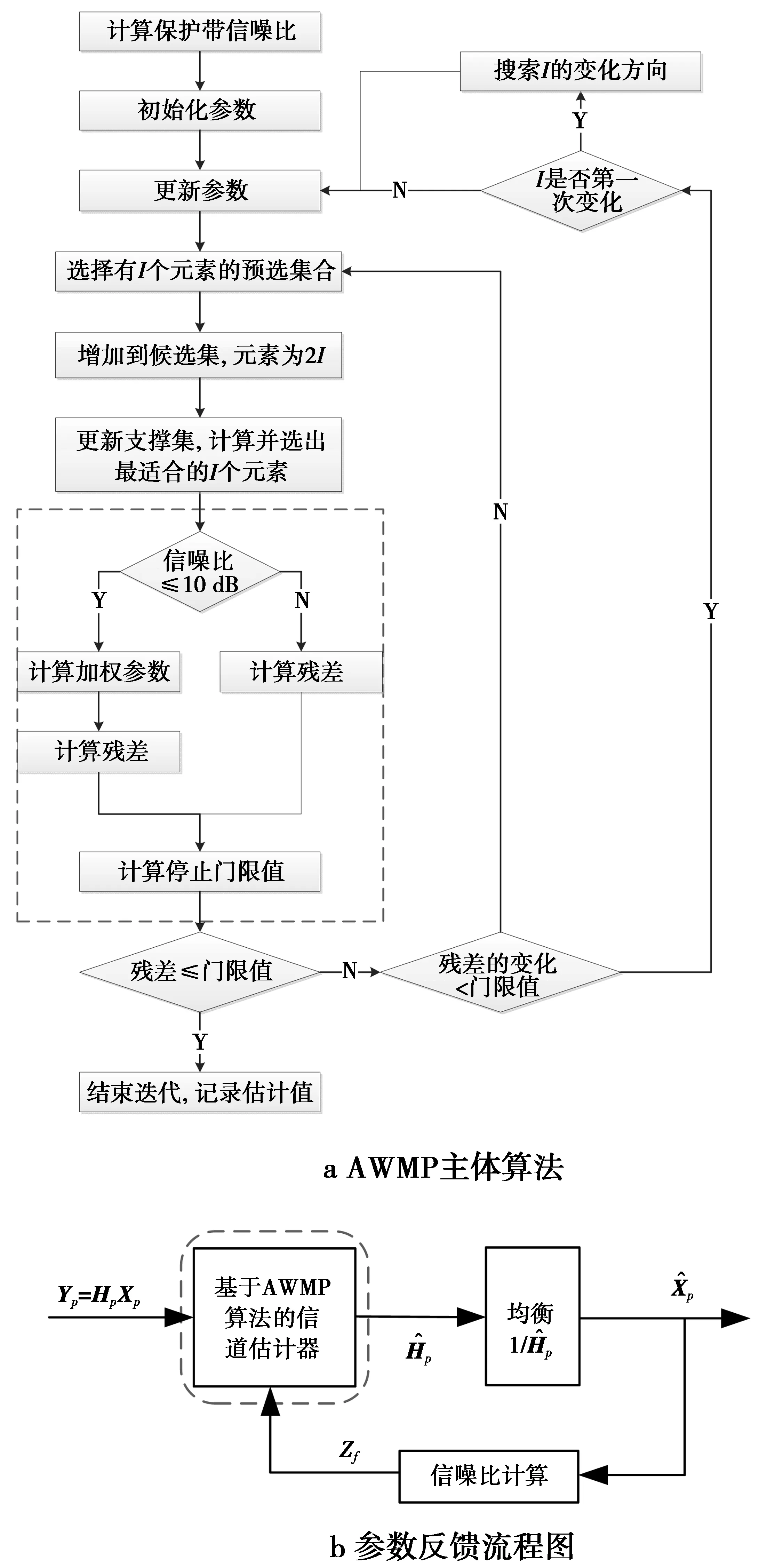
图2　自适应加权匹配追踪算法流程图Fig.2　Flow chart of AWMP algorithm

算法所需的参数：迭代次数i；第i次迭代后的残差向量ri；观测集A；支撑集φi；支撑位置集Ti；支撑集大小I；第i次迭代估计的信噪比Zi。

综合图2，具体算法如下。

1)算法初始化。令r0=Yp，A=Fp，φ0=[∅]，T0=[∅]，i=1，段长B=0，初始化I等于前一次信道稀疏度K，若为第1帧，I=K=1。根据(7)式估计信噪比初始值Zw；

2)对于第i次迭代，步骤如下。

步骤1选择预选集。将|A′·ri-1|中最大I个元素值的位置保存到集合Si中；

步骤2增加候选集Ci=Ti-1∪Si，按Ci的记录位置，从A中抽取2I个元素存入φCi。

步骤4根据Ti记录的位置从φCi中删除I个元素后得到φTi。

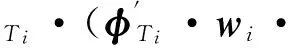
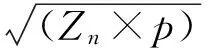
步骤7由于I等于前一次信道稀疏度K，故I是个估计值，需要进行修正。分别在I-1和I+1方向执行步骤1～步骤6，计算残差rI-1和rI+1，将残差减少较快的方向作为搜索方向，如rI-1减少快，则B=-1，否则B=1，同时更新I=I+B。若两方向的残差都增加，就将rI的信道估计值作为最终结果。

步骤8当I=I+B，继续进行步骤1～步骤8的迭代计算，直至满足步骤6的条件退出。

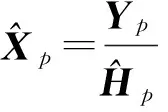
(8)

计算导频的信噪比Zf为

(9)

3　仿真分析

为了结合实际，论文的验证模块均采用长期演进(long term evolution，LTE)标准所规定的形式，使用物理下行共享信道(physical downlink shared channel，PDSCH)规定的参数[15]，采用Turbo码进行信道编码；OFDM复用带宽为20 Mbit/s，1 200个有效子载波占用中间18 Mbit/s带宽，前后分别1 Mbit/s的保护带宽；导频序列为Zadoff-Chu序列；随机生成基带数据；试验共发送10 000个OFDM符号，采用正交相移键控(quadrature phase shift keying，QPSK)进行调制。

3.1信道估计精度对比

选择多径信道模型。初始K1=10，Ki=Ki-1+v,v=[-2,-1,0,1,2],Ki∈[0,20]。多径的离散延时位置与归一化幅度随机生成。然后根据文献[16]接收端高概率恢复信道信息的条件P≥v×K×log(N/K)(其中，v为常数，N为子载波数，P为导频数)得到导频。通常，P为4K～8K，即插入的导频数为前一次信道稀疏度的4～8倍。仿真中，P=4K或P=8K。仿真参数如表1所示。

表1　仿真参数Tab.1　Simulation parameters

AWMP，LS和OMP的误码率对比图如图3所示。

图3　AWMP，LS和OMP的误码率对比图Fig.3　Comparison of BER for AWMP, LS and OMP

从图3可以看出，在相同信噪比的条件下，基于AWMP算法的信道估计误码性能最好。随着信噪比的增加，其误码率下降更明显。在导频数目相同的情况下，AWMP算法的准确性较OMP算法高，分析图3中性能最好的2个曲线可知，即使采用2倍导频数目的OMP算法进行重构信息，其误码率也要略高于AWMP算法的误码率。从而证实了AWMP算法能利用较少的导频准确进行信道估计的观点。

图4为采用AWMP、传统LS和OMP算法的信道估计MSE。

图4　AWMP，LS和OMP的信道估计均方误差对比图Fig.4　Comparison of channel estimation and MSE for AWMP, LS and OMP

衡量信道估计精度的参数可表示为

(10)

(10)式中，M为蒙特卡洛值。分析图4可知，在压缩感知信道估计过程中，本文利用前一个符号的信道稀疏度对后一符号信道稀疏度进行平滑搜索，加之利用均衡后的反馈信息，提高了压缩感知信道估计的准确度，进而降低了信道估计的均方误差。

3.2算法复杂度计算分析

信道估计需实时反映信道的状态信息，因此，计算复杂度十分重要。通过对上述AWMP算法步骤的分析，若用乘法执行次数衡量算法的计算复杂度，那么一次迭代中，步骤5的乘法次数最多，即每次迭代的计算复杂度为O(P2K2)，其中，P表示插入的导频子载波个数，K表示信道的稀疏度。

4　结束语

本文针对OFDM系统中传统压缩感知信道估计算法的不足，提出一种AWMP算法。该算法根据信噪比估计值进行自适应加权，解决了OMP算法因加权带来的不足。同时，利用类似退火算法寻找出最优稀疏度。此外，AWMP算法中采用均衡后的导频信噪比修正信噪比估计值，利用多次迭代不断提高信噪比和稀疏度的估计精度，使信道时域脉冲响应更加准确。仿真结果表明，与传统算法相比，采用AWMP算法进行信道估计的误码率和均方误差更低。

[1]TAUBOCKG,HLAWATSCHF.AcompressedsensingtechniqueforOFDMchannelestimationinmobileenvironmentsexploitingchannelsparsityforpilots[C]//IEEE.Acoustics,SpeechandSignalProcessing,ICASSP2008，IEEEInternationalConferenceon.LasVegas,NV:IEEE, 2008: 2885-2888.

[2]TONGL,SADLERBM,DONGM.Pilot-assistedwirelesstransmissions[J].IEEESignalProcessingMagazine, 2004, 21(6): 12-25.

[3]LIY.PilotsymbolaidedchannelestimationforOFDMinwirelesssystems[J].IEEETransactionsonVehicularTechnology, 2000, 49(4): 1207-1215.

[4]戴琼海, 付长军, 季向阳. 压缩感知研究[J]. 计算机学报, 2011, 34(3): 425-434.

DAIQionghai,FUChangjun,JIXiangyang.Researchoncompressedsensing[J].Chinesejournalofcomputers, 2011,34(3):425-434.

[5]PAREDESJL,ARCEGR.Ultra-WidebandCompressedSensing:ChannelEstimation[J].IEEEJournalofSelectedTopicsinSignalProcessing, 2007, 1(3): 383-395.

[6]CHENBaohao,CUIQimei,YANGFan.Compressedsensingbasedchannelestimationusedinnon-sample-spacedmultipathchannelsofOFDMsystem[J].TheJournalofChinaUniversitiesofPostsandTelecommunications, 2015, 22(2):31-37.

[7]TROPPJ,GILBERTA.Signalrecoveryfromrandommeasurementsviaorthogonalmatchingpursuit[J].IEEETransactionsonInformationTheory, 2007, 53(12): 4655-4666.

[8]CHENSS,DONOHODL,SAUNSERSMA.Atomicdecompositionbybasispursuit[J].SIMAJournalofScientificComputing, 1998, 20 (1):33-61.

[9]SUNDMAND,CHATTERJEES,SKOGLUNDM.Greedypursuitsforcompressedsensingofjointlysparsesignals[C]//IEEE.SignalProcessingConference,2011，19thEuropean.Barcelona:IEEE, 2011: 368-372.

[10]ABOUTORABN,HARDJIAWANAW,VUCETICB.ApplicationofcompressivesensingtochannelestimationofhighmobilityOFDMsystems[C]//IEEE.Communications(ICC), 2013IEEEInternationalConferenceon.Budapest:IEEE, 2013: 4946-4950.

[11]ROMBERGJ.Thedantzigselectorandgeneralizedthresholding[C]//IEEE.InformationSciencesandSystems, 2008.CISS2008. 42ndAnnualConferenceon.Princeton,NJ:IEEE, 2008:19-21.

[12]CAITT,XUGuangwu,ZHANGJun.Onrecoveryofsparsesignalsvial1minimization[J].IEEETransactions, 2009, 55(7): 3388-3397.

[13]DOTT,GANL,NGUGENNH.Sparsityadaptivematchingpursuitalgorithmforpracticalcompressedsensing[C]//IEEE.Signals,SystemsandComputers, 2008 42ndAsilomarConferenceon.PacificGrove,CA:IEEE, 2008: 581-587.

[14]PANCY,DAILL.TimedomainsynchronousOFDMbasedoncompressivesensing:anewperspective[C]//IEEE.GlobalCommunicationsConference(GLOBECOM), 2012IEEE.Anaheim,CA:IEEE, 2012:4880-4885.

[15] 3GPP.TS36.212v11.3.0，Evolveduniversalterrestrialradioaccess(E-UTRA);multiplexingandchannelcoding(Release11)[S].France:ETSI, 2013.

[16]TROPPJA,GILBERTAC,STRAUSSMJ.Simultaneousspareapproximationviagreedypursuit[C]//IEEE.Acoustics,Speech,andSignalProcessing, 2005.Proceedings. (ICASSP'05).IEEEInternationalConferenceon.Philadelphia:IEEE, 2005: 721-724.

余翔(1964-)，男，重庆人，博士，教授，主要研究方向为无线通信系统。E-mail:gayuxiang@tom.com。

郑寒冰(1991-)，女，安徽宿州人，硕士研究生，主要研究方向为无线通信系统。E-mail: 645955527@qq.com。

曾银强(1990-)，男，四川成都人，硕士研究生，主要研究方向为无线通信系统。E-mail：1872143834@qq.com。

(编辑：王敏琦)

The National Science and Technology Specific Program of China (2014ZX03003004-003)

Adaptive weighting & matching pursuit algorithm based on compressed sensing

YU Xiang, ZHENG Hanbing, ZENG Yinqiang

(School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R. China)

Compressed Sensing (CS) technology can improve the spectrum efficiency by reducing transmitted pilots. In order to estimate the pilot-aided and sparse-unknown channel utilizing compressed sensing in OFDM system, an adaptive weighting & matching pursuit (AWMP) algorithm is proposed. The algorithm estimates the time-domain channel impulse response by using the proposed method, weights adaptively and searches optimal sparse degree after iteration by the estimated signal to noise ratio (SNR) and the matching principle. Then the channel information is estimated accurately without knowing SNR and sparse degree. Simulation indicates that, compared to the traditional channel estimation algorithm, the method proposed here can obtain lower bit-error-rate (BER) and mean square error (MSE) with fewer pilots.

compressed sensing; channel estimation; sparsity; signal to noise ratio(SNR); adaptive weighted; matching pursuit

10.3979/j.issn.1673-825X.2016.05.015

2015-07-26

2016-04-11通讯作者：郑寒冰645955527@qq.com

国家科技重大专项课题(2014ZX03003004-003)

TN911.23

A

1673-825X(2016)05-0707-06