水下重锤夯击能及夯击效果试验研究

刘苏乐，石 崇，梁邦炎

(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2.河海大学 岩土工程科学研究所，江苏 南京 210098；3.中交第四航务工程局有限公司，广东 广州 510000)



水下重锤夯击能及夯击效果试验研究

刘苏乐1,2，石 崇1,2，梁邦炎3

(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2.河海大学 岩土工程科学研究所，江苏 南京 210098；3.中交第四航务工程局有限公司，广东 广州 510000)

重锤夯实是水下抛石基床密实工艺中的重要方法。根据流体动力学，本文建立夯锤在水中运动的计算模型，然后通过室内缩比尺试验，得到了夯锤水下绕流阻力系数经验取值；最后探讨了不同夯锤几何、不同落距对夯实效果的影响。结果表明：圆台型夯锤与圆柱形夯锤相比，由于有倒角，在水中的绕流阻力系数可以小至1.0；同一夯击能作用下不同锤型对抛石基床的夯实效果相差在5%之内；同一夯锤不同落距作用下，落距越大，抛石基床沉降量越大，夯击应力越大，但抛石基床沉降率存在一个极限值。

夯锤；绕流阻力系数；水下抛石基床；有效夯击能

在港口、抛石护岸等建设项目中，重锤夯实法是抛石基床密实经常采用的施工工艺[1-3]。对水下重锤夯击能分析、研究对完善重锤夯实工艺具有重要意义[4-5]。针对水下重锤夯击能问题，王德利[6]对水下夯锤夯击能进行了分析，发现夯锤水下运动存在一个极限速度。谢立全等[7]研究表明：改善夯锤倒角、倾角，增大泄水孔有利于减少绕流阻力，提高夯实效率。叶峰等[8]通过重锤夯实抛石基床现场试验和室内试验的研究，提出采用超重锤来增加抛石基床分层厚度，改善后的施工效率显著提高。童新春等[9]利用有限元流固耦合方法对夯锤进行建模，并考虑浮力的条件下对夯锤在水中下落过程进行计算，得到了夯锤绕流阻力系数值为1.166。Luo等[5]基于物理量纲分析，建立了夯击应力与不同重锤夯击工况之间的方程，该预测方程也为探究地基夯击作用后地基特性提供了一种新的方法。Poran等[10]在尺寸为122cm×122cm×122cm的模型箱中进行强夯法加固波斯顿干砂地基的试验，得到一些基于试验结果的设计曲线。L.与Beine[11]通过室内试验提出动应力随深度的增加呈指数形式衰减。在以上研究中，已经初步探讨了水下重锤夯实效果，但尚缺少系统的实验验证，也没有考虑不同锤型、不同落距对抛石基床夯击效果的影响。 本文基于夯锤水下运动规律平衡方程，采用室内缩比尺试验得到了不同锤型重锤水下绕流阻力系数，为工程中锤型选择提供依据；在此基础上研究相同夯击能不同锤型、同一锤形不同落距对抛石基床试验效果的影响；以期为工程实践中锤形选择提供借鉴。

1　夯锤水下运动规律分析

1.1夯锤水下运动理论分析

夯锤在水中自由下落过程中，受浮力与绕流阻力的影响，存在极限运动速度，且有效夯击能随落距的增加而减小，而这一过程与夯锤形状、流体性质、流体雷诺数、相对粗糙程度等因素有关[12]。为了分析夯锤在水中自由下落时的运动规律，如图1设重锤在水中基础上方H处由静止开始下落，当下落距离为x时，作用在重锤上的力分别为：自重Mg，浮力F浮,水体阻力Fz。重锤在三力作用下作加速、或匀速运动，夯锤运动方程可由式(1)所示：

Mg-ρwgv-Fz=Ma

(1)

其中，V为重锤体积，Fz为运动水体对静止夯锤的绕流阻力，工程中通常可用式(2)表示:

Fz=Cfωρwv2/2

(2)

式中，Cf为绕流系数；v为重锤与水体间的速度；ω为夯锤垂直于运动方向的投影面积；ρw为水的密度。根据位移x、速度v、加速度a的物理意义，上式可进一步整理为:

(3)

相关文献表明，绕流阻力系数与锤形、流速、流体雷诺数等因素有关，为简化问题，假设绕流系数为常数，相关文献[6]研究表明圆台重锤的Cf一般处于1.2～1.6之间，如果取为定值，则上式(3)为二阶常系数微分方程。

(4)

当x=H时的速度vH为重锤夯击速度。因此，在一定落距H下若已知绕流系数、夯锤底面积、重锤质量，即可方便的计算出有效夯击能。

但是绕流阻力系数与重锤形状、水流与重锤间的相对速度、雷诺数等因素密切相关，在重锤下落的过程中并非定值[9]，常规方法只能借助经验对绕流系数取值[13-14]。结合室内实验，本文针对圆台与圆柱形重锤的水下运动对其绕流阻力进行分析。

1.2夯锤水下运动室内试验研究

对重锤水下运动规律的监测仪器采用加速度传感器，其性能满足采样频率大于500 Hz、大水深防水要求，可实时测试不同时刻的垂向加速变化情况。

表1　试验主要参数

通过模型试验分析圆柱型重锤和与圆台型重锤水中下落规律，主要进行了如下工况：水深110 cm，夯锤落距95cm，圆台型夯锤重5.9 kg，底面直径11cm；圆柱形夯锤重5.7 kg，直径12cm，具体参数如表1所示。

1.3试验结果分析

通过夯锤试验，测得了不同夯锤下落距离与瞬间速度的数据，与理论公式(4)推出的落距与速度值进行拟合，得到了圆柱形夯锤和圆台型夯锤实测曲线与拟合曲线的对比图；进而得出Cf平均值，可以得到5.7 kg圆柱形夯锤的平均绕流阻力系数为1.55；5.9 kg圆台型夯锤的水中平均绕流阻力系数为1.0。

通过试验，发现相对于圆柱形夯锤，圆台型夯锤在水中的绕流阻力系数较小，受到的阻力较小，得到在同等条件下，优先选用圆台型夯锤夯击抛石基床。

2　不同锤型夯锤对抛石基床夯击试验研究

为了分析同一有效夯击能条件下不同锤型对抛石基床的夯击效果，选用5.7 kg圆柱型夯锤及4.9 kg圆柱型夯锤在有效夯击能为879.83kJ/m2对同一厚度抛石基床进行夯击试验。

为了使室内试验与现场工艺、试验相对应，按照现场工艺或者现场试验所有尺寸进行等比例缩小进行室内试验是一种较为可行的方法。本次室内试验综合考虑了夯锤尺寸、试验容器大小、抛石粒径、抛石厚度、夯锤落距的选取等因素，根据现场工艺与现场试验按照1:10进行室内缩比尺夯击试验。

2.1试验仪器

根据抛石基床在夯锤夯击下具有夯击应力大、持续时间短的特点，本次对夯击应力监测选用MPM426W型智能液位变送器。

抛石基床作为工程常用的基础形式，规范要求抛石质量范围为10 kg～100 kg，通过计算相应的粒径范围为0.1m ～0.3m。按照1:10进行缩比尺试验，相应的抛石粒径范围为0.01m～0.03m。为了观察抛石基床夯击试验过程，抛石基床夯击试验均在透明的玻璃容器中进行。本次试验制作了钢骨架的容器，将夯击应力监测仪器放入钢制容器正中位置处，用铁链及扎带对监测仪器进行固定。夯击应力监测仪器电缆用塑料管进行保护，塑料管需用扎带规定在钢制容器上。往钢制容器中倒入一定厚度松散的0.01m～0.03m抛石体，使用吊机将钢制容器吊入玻璃容器中。

在夯锤夯击作用时，监测仪器监测数据需经专业仪器作进一步转化处理。

2.2试验工况及结果分析

在夯击对抛石基床进行松散处理，采用4.9kg圆柱形夯锤，水中落距0.30m对0.2m抛石基床采用压半夯夯击，得到各夯击点位夯锤夯击时夯击应力监测仪器所监测到夯击应力大小如表2所示。从表中可以看出四次夯时夯击应力最大值为21.50kPa，八次夯时夯击应力最大值为27.84kPa。记录夯锤每个点位夯击时夯击应力监测仪器监测到的夯击应力值如表2所示；表中字母与坐标对应为：a-(0.35,0.35)b-(0.35,0.4)c-(0.35,0.45)d-(0.4,0.35)e-(0.4,0.4)f-(0.4,0.45)g-(0.45,0.35)h-(0.45,0.4)i-(0.45,0.45)，单位：m。

表2　圆柱形、圆台型夯锤不同夯击点位时监测仪器监测到的夯击应力值(kPa)

表3　圆柱形、圆台型夯锤夯击不同夯沉量监测点各夯次夯沉量(m)

在同一夯击能作用下，通过对圆台型夯锤与圆柱形夯锤对抛石基床的夯击效果做对比，从表3中可以看出圆柱形夯锤0.3m落距四夯次时抛石基床平均沉降量为0.0235m，八次夯为0.010 3m，累加夯沉量为0.0338 m；圆台型夯锤0.3m落距四夯次时抛石基床平均沉降量为0.0245m，八次夯为0.0125m，累加夯沉量为0.037 m，两者对抛石基床夯实效果差别不大。从表3及图2中可以看出圆柱形夯锤四次夯中间点的夯击应力为21.5kPa，八次夯为27.84kPa；圆台型夯锤四次夯中间点夯击应力为22.3kPa，八次夯为26.95kPa。可以看出，夯击应力的值也差别不大。

3　水下夯锤不同落距对抛石基床夯击效果影响

针对水中不同夯锤落距条件下抛石基床的室内夯击试验，其中夯锤水中落距选为0.2、0.24、0.3、0.4m四种工况，抛石基床厚度选为0.2m(夯击应力监测仪器顶面至抛石基床顶面距离)。夯锤选用圆柱形，上下底面半径为0.05m，高为0.08 m，体积为6.28×10-4m3，密度为7850 kg/m3，相应的质量为4.9 kg。采用压半夯对抛石基床进行两夯遍夯击，夯击应力监测点布置在抛石基床底面的正中位置处，沉降量监测点选取4个，布置在抛石基床顶面位置处。相应的夯锤夯击位置、沉降量监测点以及夯击应力监测点布置的俯视图如图3所示。

4.9 kg圆柱形夯锤在水中落距0.2、0.24、0.3、0.4m分别对抛石基床进行四次夯、八次夯，夯锤水下每一次落距对抛石基床进行夯击试验后，需对抛石基床进行松散处理。记录夯锤每个点位夯击时夯击应力监测仪器监测到的夯击应力值如表4所示；表中字母与坐标对应为：a-(0.35,0.35) b-(0.35,0.4) c-(0.35,0.45) d-(0.4,0.35) e-(0.4,0.4) f-(0.4,0.45) g-(0.45,0.35) h-(0.45,0.4) i-(0.45,0.45)，单位：m。

从表4中0.2m落距可以看出，夯锤四夯次时所监测到的夯击应力最大值为13.3kPa，夯锤八夯次时所监测到的夯击应力最大值为15.1kPa，夯锤八夯次较四夯次时所监测到的夯击应力值提高13.53%，夯击应力有较大的增加幅度，出现这种现象一是由于四次夯时抛石基床存在夯沉量间接的增大了夯锤落距，另一个原因是由于经过夯击抛石基床更加密实，夯击应力的传递效果更好。

从表4中同时可以得到，0.24、0.3、0.4m落距条件下四夯次时夯击应力最大值分别为16.49、21.50、29.92kPa；八夯次时夯击应力分别为25.39、27.84、32.15kPa。

对抛石基床夯沉量4个监测点进行监测得到各监测点四夯次、八夯次时夯沉量的大小值如表5所示。

表4夯锤不同夯击点位时监测仪器监测到的夯击应力值(kPa)

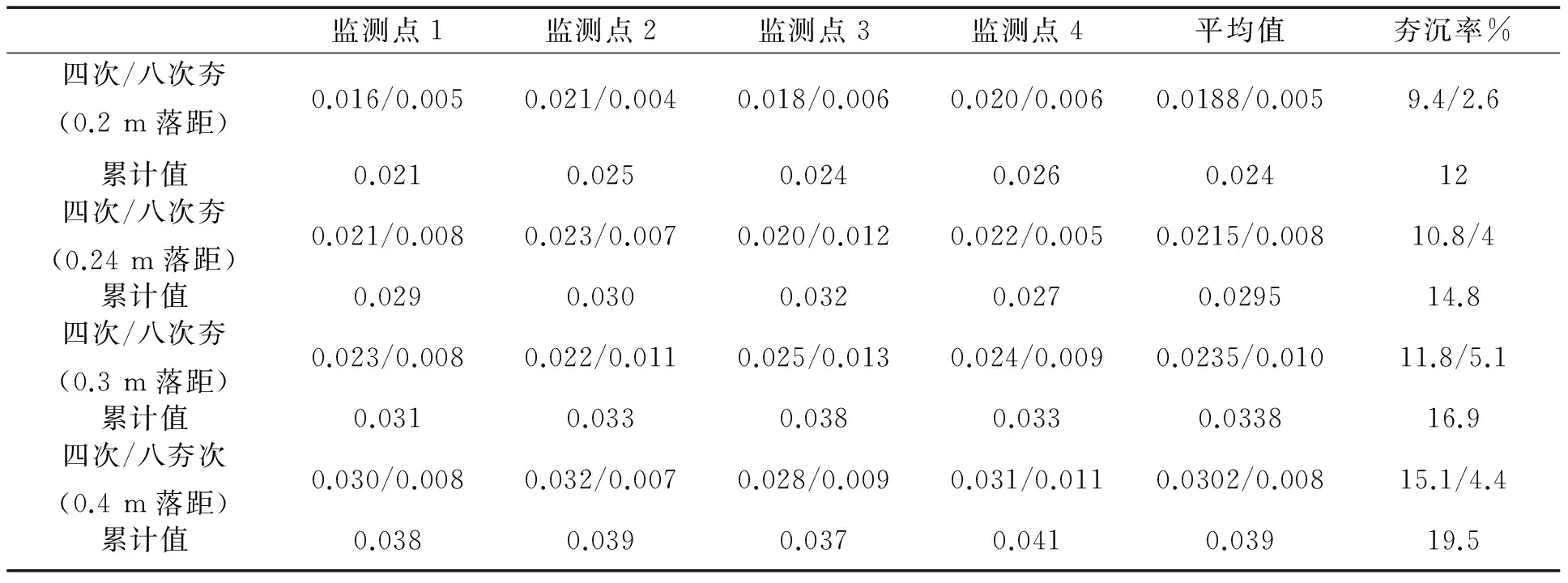
表5不同夯沉量监测点夯沉量(m)

从表5中可以得到，夯锤落距0.2、0.24、0.3、0.4m时，可以得到抛石基床四次夯沉降量分别为0.018 8、0.0215、0.0235、0.030 2m；相应的夯锤率分别为9.4%、10.8%、11.8%、15.1%；相应的八次夯夯沉量分别为0.0053、0.008、0.010 3、0.008 8m；夯沉量分别为2.6%、4%、5.1%、4.4%；累计夯沉量平均值分别为0.024、0.029 5、0.0338、0.039m，累计夯沉率分别为12%，14.8%，16.9%，19.5%。

对夯锤不同水中落距条件下对抛石基床夯击应力进行对比，得到夯锤四次夯、八次夯时夯击应力最大值随夯锤落距的变化曲线如图4(a)所示。从图中可以看出，四次夯时夯击应力随着夯锤水中落距的增加呈线性增加；八次夯时夯击应力也随着夯锤水下落距的增加而增加，但随着夯锤水下落距的增加夯击应力的增加幅度呈减小趋势。

0.20 m厚抛石基床在4.9 kg夯锤不同落距条件下夯击，相应的夯沉率随夯锤落距的变化曲线如图4(b)所示。从图中可以看出随着夯锤落距的增加，四次夯时抛石基床夯沉率随着夯锤落距的增加而相应增加，抛石基床的夯沉率从夯锤落距为0.20 m时的9.4%，逐渐增加到夯锤落距为0.40 m时的15.1%。对于八夯次时抛石基床的夯沉率随夯锤落距的增加夯沉率有增大的趋势，但增加不明显，甚至出现减小的现象，出现这种现象进一步说明抛石基床夯沉率存在极限值。

4　结论

1)针对重锤水下绕流阻力试验，得到圆柱形夯锤的水下绕流阻力平均值为1.5，圆台型夯锤的水下绕流阻力系数平均值为1.0。结果表明，在同等条件下，圆台型夯锤具有较小的绕流阻力系数，工程中应优先选用圆台型夯锤夯击抛石基床，并设置一定的泄流孔。

2)在对不同锤型相同夯击能夯击试验中，得到圆柱形夯锤累计夯沉量为0.0338 m，八次夯中间点应力为27.84kPa；相应的圆台型夯锤累计夯沉量为0.037 m，八次夯中间点应力为26.95kPa。结果表明，圆台型夯锤对抛石基床的夯击效果较好一些，但差别不大，因此采用夯击能近似评价夯实效果可行。

3)通过夯锤不同落距的四次夯，八次夯试验，随着夯锤落距的增加，四次夯时抛石基床夯沉率随着夯锤落距的增加而相应增加，抛石基床的夯沉率从夯锤落距为0.20 m时的9.4%，逐渐增加到夯锤落距为0.40 m时的15.1%。对于八夯次时抛石基床的夯沉率随夯锤落距的增加夯沉率有增大的趋势，但增加不明显，甚至出现减小的现象，出现这种现象进一步说明抛石基床夯沉率存在极限值。

[1]李良英.大质量夯锤在嵩屿码头水下基床夯实中的应用[J].港工技术, 2009(05): 46-49.

[2]蔡劼刚.用爆破夯实法处理水下拋石基床[J].港口工程, 1990(05): 26-28.

[3]赵敏成.关于水下抛石基础的夯实问题[J]. 水运工程, 1988(08): 54-58.

[4]李俊如, 高建光, 贺 涛,等.广西钦州港二期码头抛石基床的水下爆夯[J]. 岩土力学, 2004, 24(6):917-921.

[5]冯世晖, 庞善喜.重力式码头基础施工过程控制[J].水运科学研究, 2007: 2(10):29-30.

[6]王德利.不同夯锤的水下夯实效果及夯锤阻力理论在水下夯实中的运用探讨[J].水运工程, 1990, 03:51-53.

[7]谢立全，戚健文等，水下抛石基床重锤夯实及夯锤工作性能数值分析[J]全国水工岩石力学学术会议, 2010.

[8]叶 峰.重锤夯实抛石基床的有效加固深度试验研究[J].岩土力学.2011.32(4):1008-1012.

[9]童新春.重力式码头抛石基床重锤夯实施工效率改进研究[J]. 水运工程, 2013,(03): 199-203.[10]SI-HAI LUO, YANG WANG, XIAO-QING PANG, et al. An empirical study on the estimation of soil properties of loess ground after dynamic compaction[J]. Pavement and Geotechnical Engineering for Transportation,2013,106, 93-101.

[11]PORAN C J, RODRIGUEZ J. A design of dynamic compaction[J]. Canadian Geotechnical Journal, 1992,29(5): 7976-802.

[12]王德利.水下夯锤的冲击能.水运工程[J], 1985(1): 35-37.

[13]李 霞, 陈徐均, 孙芦忠,等. 基于动网格的物体下沉运动的二维数值模拟[J]. 港工技术, 2010, 47(1):4-7.

[14]ZHU L, WANG J, CHENG N S, et al. Settling Distance and Incipient Motion of Sandbags in Open Channel Flows[J].American Society of Civil Engineers, 2014, 130(2):98-103.

(责任编辑李军)

Water hammer tamping energy and the experimental study on compaction effect

LIU Sule1,2, SHI Chong1,2, LIANG Bangyan3

(1.Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing,Jiangsu 210098, China; 2. Research Institute of Geotechnical Engineering, Hohai University, Nanjing,Jiangsu 210098, China;3.CCCC Fourth Harbor Engineering Co.,Ltd3,Guangzhou 510000，China)

Heavy tamping method is a kind of important method of rubble bed tamping in the construction, the heavy hammer tamping energy is an important indicator of impact compaction hammer effect, the hammer tamping energy can be influenced by hammer type, flow resistence, drop distance and other effects. Therefore, on the basis of fluid dynamics. First of all, establish the calculation model of the hammer in water movement, analyse the hammer flow resistance in the process of hammer in water movement, and then through the indoor shrinkage scale test, analyse the water movement law of the cylindrical and cone hammer ,obtain the experiential tamping hammer water flow coefficient value. Finally, analyse of the different geometric rammer, different distance to the effect of compaction effect. The results show that a cone type tamping hammer and cylindrical rammer compared. Because of the chamfer of a cone type hammmer, flow resistence coefficient is smaller in water and the value is about 1.0. under the action of the same tamping energy, different types of hammer has difference in 5% on the rubble mound foundation compaction effect.with a hammer in different falling distance, the greater the falling distance is,the greater the amount of settlement of riprap foundation bed is, the bigger the compaction stress is. but rubble mound foundation settlement has a limit value. The research results can provide reference for the selection of hammer shape under the process of compaction.

rammer; flow resistance coefficient; underwater rubble bed;effective hammering energy

2016-05-12

国家重点基础研究发展计划(973计划)(2015CB057903)；国家自然科学基金青年项目(51309089)；江苏省基础研究计划(自然科学基金)(BK20130846)

刘苏乐(1991-)，男，江苏连云港，硕士，研究方向：岩石力学与工程安全。

1673-9469(2016)03-0057-06

10.3969/j.issn.1673-9469.2016.03.012

TV

A