恒流供电网络可靠性分析与优化*

管仁竹　王心太　樊　诚

(92665部队　慈利　427200)



恒流供电网络可靠性分析与优化*

管仁竹王心太樊诚

(92665部队慈利427200)

展开寿命周期内恒流供电网络劣化规律的研究，是电力行业可靠性研究中的重要内容。引入故障率因子描述恒流分支模块与支线负载数量的关系，建立了远供系统的多态可靠性模型。运用遗传算法求解模型，分析各因素对系统可靠度的影响。仿真结果表明：当给定系统总供电功率时，随着干、支线负载数量的变化，存在使系统可靠度最大的分配方式，可以辅助预防式维修周期的制定；适当增加支线负载数量可以显著提升系统供电效能。

恒流供电网络; 恒流分支; 可靠性; 多态

Class NumberTN915.02

1　引言

供电系统是网络通信及状态检测等功能正常运行的根本保证，而恒直流供电与现有供电方式相比具备抵抗接地故障、故障点定位简单等优势[1～4]，但是一直存在恒流分支的难题。文献[5～6]提出了恒流分支功能较好的实现方式，并详细分析了其热耗散等一系列可靠性指标，最后通过电路仿真实验，验证了该型恒流供电系统组网后，对短路接地故障的自适应恢复特性，使得恒流供电的工程应用具备可行性，但由于财力原因，提出这些方案的ARENA项目并没有实际开展建设[7]，因此，恒流分支部件对恒流供电系统可靠性影响方面的工作开展还比较少，有必要分析恒流供电网络在寿命周期内的系统可靠性变化情况，为恒流供电网络的设计以及维修决策提供技术支持。

多数文献在分析可靠性问题时，常常假设系统部件为两态，即运行或者失效，而在许多情形下，部件的状态往往多于两种，因此基于多态理论分析系统可靠性更加符合实际。近年来针对复杂系统的可靠度建模成果指出冗余性越高可靠度越高并不适用于多态的情况，增加多态部件可能提升也可能降低该系统的可靠度[8～10]，这取决于系统中主要部件的失效模式和系统本身的结构配置，以及冗余部件的数目。

本文基于多态理论，引入故障率因子来表征支线负载数量与恒流分支部件失效概率之间的关系，建立了供电网络在寿命周期内的可靠度模型。采用遗传算法，分别仿真分析了在系统总供电功率约束下，系统可靠度与支线负载数量的关系；不同系统总供电功率对远供系统结构的影响。

2　恒流供电网络系统结构

恒流分支供电是可行的，但需要将一路输入的恒流转换为两路电压值较低的恒流。为了实现这个目的，需要在网络分支位置(如图1部件A位置处)放置恒流分支设备，将一路输入恒流(如1A)转换为两路电压值较低的恒流(皆为1A)输出，一路沿着主干线继续输送，另一路输出至支线，同时，支线与主干线电流值相等，恒流源放置于两端，为了提高可靠性每个恒流源均具备单独为全网供电的能力，具体的电路设计及分析可以参考文献[5～6]。由于单个恒流分支设备的输出功率有限，实际应用中可采用多个恒流分支设备串联的方式提高其输出功率。

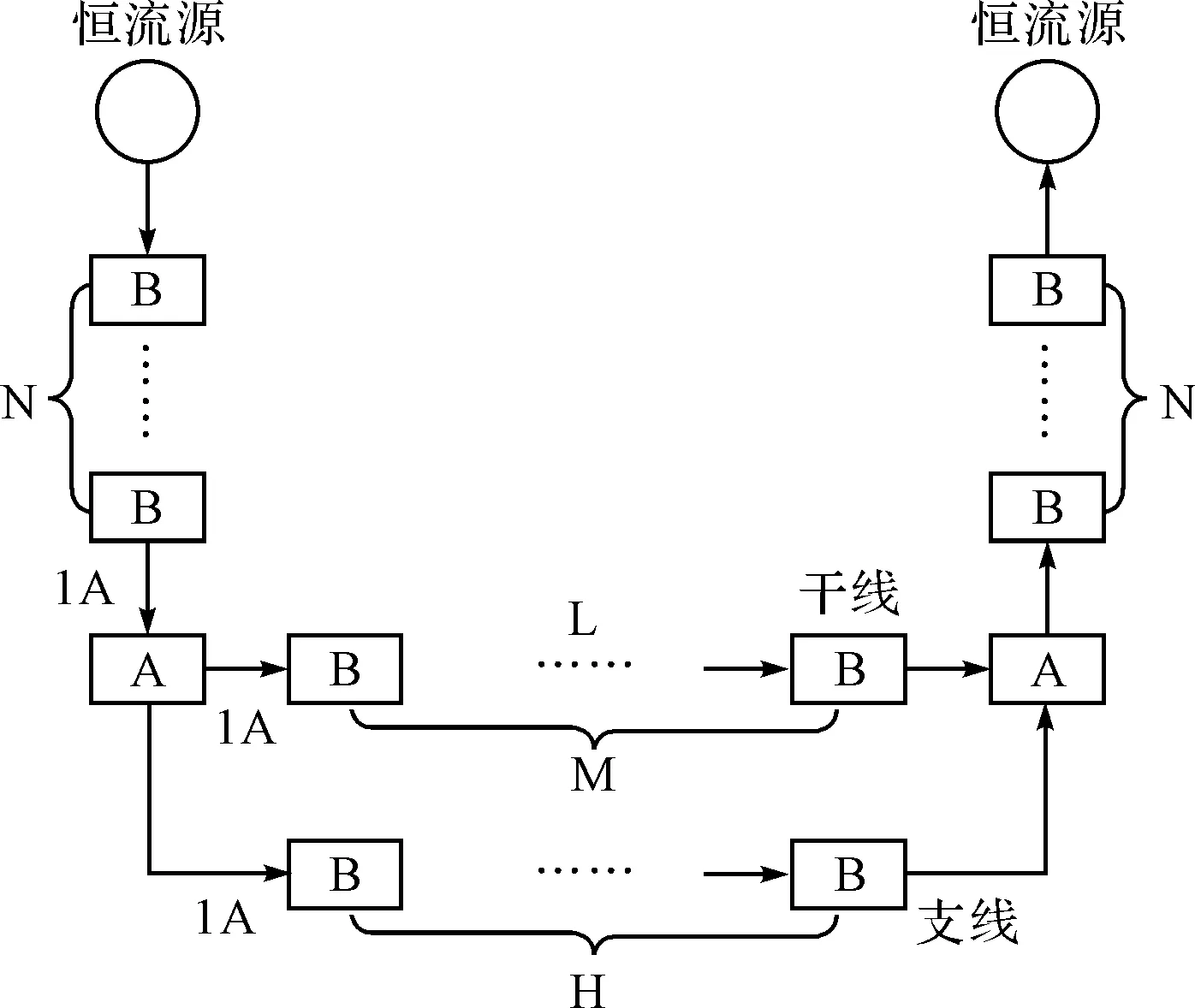
图1　恒流供电网络示意图

3　恒流供电可靠性模型

3.1模型分析

经上节分析，可将供电部件分为两类，一类为恒流分支部件(记为A)，另一类是承担恒流转恒压为设备供电的部件(记为B)，即负载。参考供电电路的主要故障模式，可将这两类供电部件的状态分为三种：正常运行、开路失效和短路失效。

分析文献[5～6]中部件A的电路结构可知，其内部恒流分支设备的数量会随着支线负载数量的增加而增加，因此，部件A的可靠性与部件B的数量之间存在相关关系，这里引入故障率因子来描述，将部件A的失效概率与支线中部件B的数量之间的关系定义为

部件A开路失效概率：

qoA(t)=qo(aHt),t∈(0,T)

(1)

部件A短路失效概率：

qsA(t)=qs(aHt),t∈(0,T)

(2)

其中H为支线中部件B的数量，qo(t)，qs(t)分别为单个恒流分支设备的开路、短路失效概率，a为故障率因子，a>1。

3.2系统可靠度

图1中所示的网格型供电系统中，部件A相当于为支线供电的恒流源，该特点使得部件A与部件B具备故障相关性，例如，当主干线L段的部件B开路失效时，由于部件A此时也失效，从而支线中的部件B全体失效，因此，支线L段部件B并不能发挥传统并联结构的冗余作用。

根据上述分析，将系统可靠性定义为岸站恒流源存在回路的概率。支线中部件B的状态并不影响系统可靠性，系统为非单调关联系统，在计算系统正常供电运行可靠度时，可以将支线忽略不计，简化为只包含主干线的串联三态系统。采用事件空间法，分析图1所示系统的失效情况包括：

事件1： 主干线部件A、B至少一个开路失效。

事件2： 主干线部件A、B均短路失效。

定义以下变量：

qsA(t)、qsB(t)为部件A、B的短路失效概率；

qoA(t)、qoB(t)为部件A、B的开路失效概率；

H为支线中部件B的数量，令M+2N=Q；则系统可靠度表达式为

R(t,Q,H)=(1-qoB(t))Q(1-qoA(t))2

-qsA(t)2·qsB(t)Q

=(1-qoB(t))Q(1-qo(aHt))2

-qs(aHt)2·qsB(t)Q

(3)

与由相同2态部件构成的标准串联系统不同的是，由相同3态部件构成的串联系统在具有最优化部件数目时其可靠度最高，部件多于或少于这个数目都会造成可靠度降低，因此主干线中的部件B的数量存在一个使系统可靠度最大的最优值，此外，主干线部件A的失效概率随着支线部件B数量的增多而减小，因此，存在最优的(Q，H)组合使得在给定寿命周期(T)内，系统可靠度最大，即：

max{R(T,Q,H)}

s.t.Q>0,H>0

(4)

4　算例分析

由于式(3)为非线性方程，解析法难以求解最优组合值。本文采用遗传算法，可以较方便地求得系统可靠度与(Q，H)组合之间的关系。假设部件A、B的失效概率服从指数分布，则失效率为常数，如表1所示，故障率因子a=1.09，部件B的功率为200W。

表1　各功能模块的失效率(单位10-9/h)

1)系统总供电功率受限

系统总供电功率设计为G=6000W，布置30个部件B。经求解，当H=12时，系统可靠度最大。图2为不同的H对应的系统可靠度的变化情况。起初随着H的增加系统可靠度是增加的，这是因为支线部件的可靠度不影响系统可靠度，这时主干线上的负载数量越少，系统可靠度越高，而当支线部件增加到一定数量后，系统可靠度开始下降，因为，支线部件数量越多主干线上部件A的可靠度越低，从而导致系统可靠度的降低。

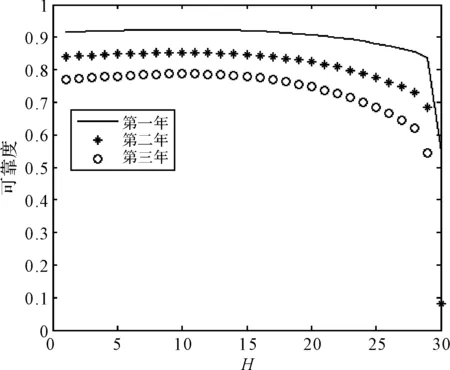
图2　系统可靠度与H的关系

实际系统运行时，多采取事后维修与预防式维修相结合的方式，而以可靠性为中心的预防式维修策略需要根据系统可靠性需求来制定预防式维修间隔。图3为不同支线部件数量对应的系统可靠度变化。若要求系统可靠度在低于0.8时，启动预防式维修，则支线部件数量为10时，维修间隔为3年，而支线部件数量为20时，维修间隔为2年，可见通过优化支线部件数量可以获得合适的维修策略。

2)系统总功率不受限

图4为系统总功率不受限时，预防性维修间隔T=3年时，系统可靠度与系统总功率的关系曲线。当系统总功率大于4000W时，最优支线部件数量始终为12，这是由于支线负载数量增多引起主干线部件A失效概率的增加对系统可靠度的影响远大于主干线上负载数量增多带来的影响，因此存在此最优值。这也说明，恒流供电系统可靠度的提高应当着重提升部件A的可靠度。

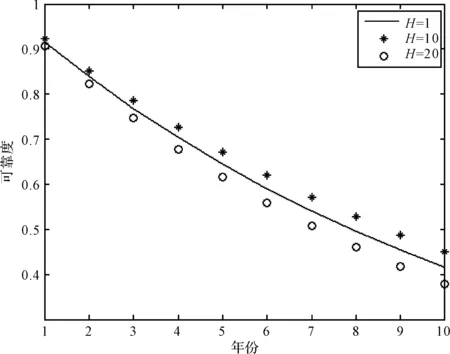
图3　系统可靠度

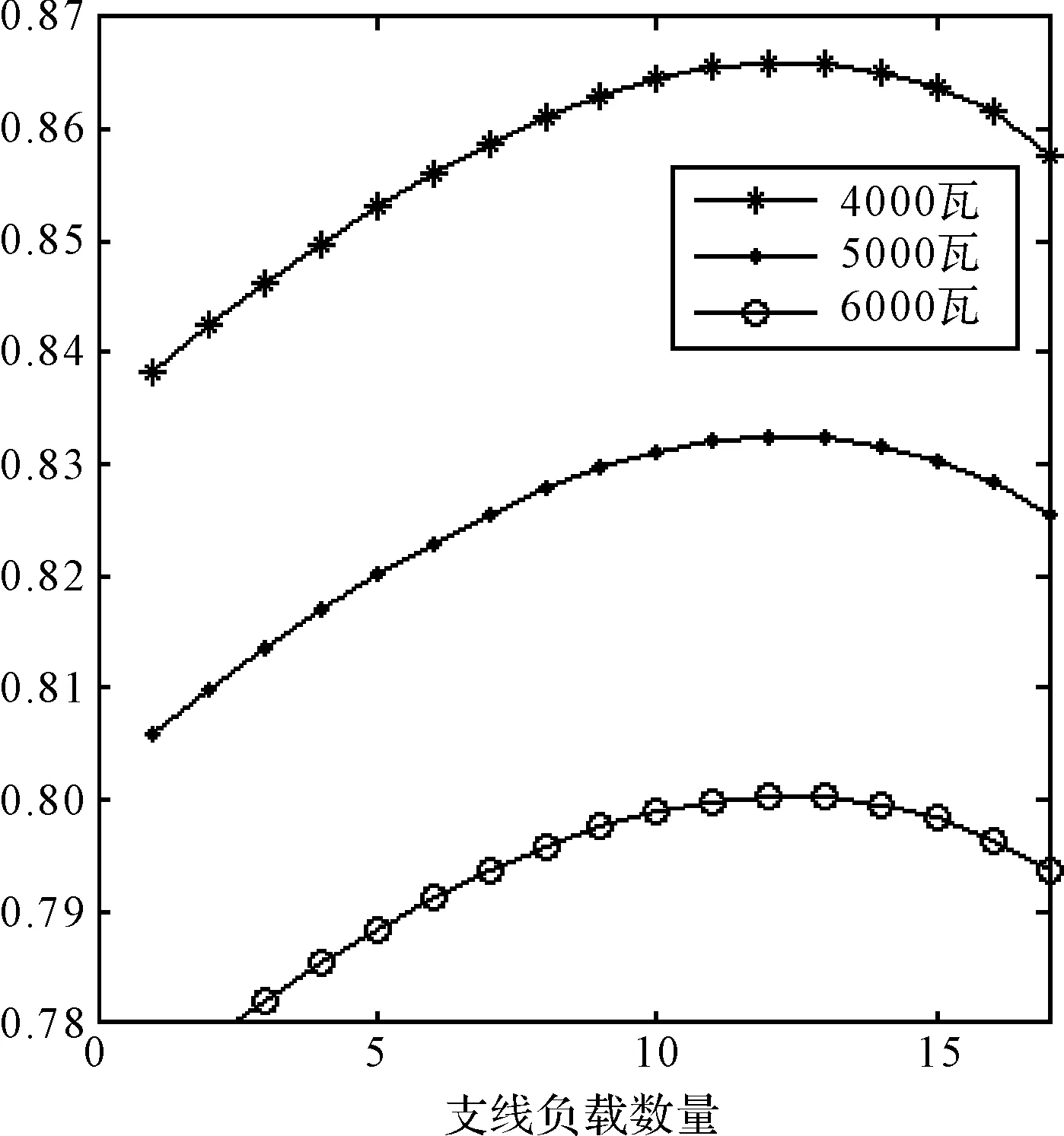
图4　系统可靠度与系统总功率的关系

5　结语

目前，恒流供电网络尚处于实验阶段，本文引入多态理论以及故障率因子建立的系统可靠度模型，考虑了恒流供电系统的实际运行情况和故障相关性，因而较符合该网络的实际运行情况。仿真结果表明，一定寿命周期内，可通过调节支线负载数量使供电系统的可靠度最大，且随着系统总供电功率的增加，支线负载数量存在上限，这是由于支线负载数量越多会造成主干线恒流分支设备可靠性越低的缘故。研究结果对于恒流供电系统的规划设计有一定意义。

[1] Person R, Aoustin Y, Blandin J, et al. From bottom landers to observatory networks[J]. Annals of Geophysics,2006,49(2)：518-593.[2] Bruce M H, Kirkham H. Power system considerations for undersea observatories[J]. IEEE Journal of Oceanic Engineering,2002,27(2)：267-274.

[3] Ting C, Liu C C. Fault location for the NEPTUNE power system[J]. IEEE Trans on Power Systems,2007,22(2)：522-531.

[4] 卢汉良,李德骏,杨灿军,等.深海海底观测网络远程电力监控系统研究[J].传感技术学报,2011,24(4)：564-569.

[5] Asakawa K, Kojima J, Muramatsu J, et al. Current-to-current converter for scientific underwater cable networks[J]. IEEE Journal of Oceanic Engineering,2007,32(3)：584-592.

[6] Asakawa K, Muramatsu J, Kojima J, et al. Feasibility study on power feeding system for scientific cable network ARENA[C]// Proceedings of MTS/IEEE Conference on Oceans,2007(5):307-312.

[7] 海洋地质国家重点实验室(同济大学).海底观测——科学与技术的结合[M]. 上海：同济大学出版社，2011. 67-70.

[8] ELSAYED A. ELSAYED. 可靠性工程[M].北京：电子工业出版社，2013:107-131.

[9] Man Cheol Kim. Reliability block diagram with general gates and its application to system[J]. Annals of Nuclear Energy,2011,38(11)：2456-2461.

[10] Ettore Bompard, Di Wu, Fei Xue. structural vulnerability of power systems : a topological approach[J]. Electric Power Systems Research,2011,81：1334-1340.

Reliability Analysis and Optimization Constant Current Power Feeding Network

GUAN RenzhuWANG XintaiFAN Cheng

(No. 92665 Troops of PLA, Cili427200)

Study on the deterioration of the constant current feeding system throughout the life of the structure is always one of the most important issues in electricity reliability engineering. Relationship between current-to-current convertor subsystem and amount of load in branch line are described by introducing failure rate. Multistate reliability model of power feeding system has been set up. Genetic algorithms to solve the model. Simulation results show that as the load configuration in trunk line and branch line changes, there is the best combination leading to maximum system reliability from the given system power. Besides, appropriate increasing amount of load in branch line can raise the system power efficiency significantly.

constant current power feeding network, current-to-current convert, reliability, multistate

2016年4月3日,

2016年5月26日

管仁竹,男,高级工程师,研究方向：网络可靠性。王心太,男,工程师,研究方向：网络可靠性。樊诚,男,博士,工程师,研究方向：网络可靠性。

TN915.02

10.3969/j.issn.1672-9730.2016.10.030