一种带变异算子的PSO算法*
余仁波 赵修平 孟凡磊
(海军航空工程学院飞行器工程系 烟台 264001)
一种带变异算子的PSO算法*
余仁波赵修平孟凡磊
(海军航空工程学院飞行器工程系烟台264001)
论文在基本PSO算法基础上,引入了遗传算法的变异算子。通过变异算子的控制函数,将PSO算法的训练过程分为前期和后期。在算法训练的前期,变异率取较大的值,以选择较多的粒子进行变异操作,目的是增强种群内部粒子的多样性,使得PSO算法能够在解空间的较大范围内进行搜索,以避免算法过早陷入局部最优解;在训练的后期,变异率取较小的值,以选择较少的粒子进行变异操作,目的是减弱种群内部粒子的多样性,使得PSO算法能够在解空间的较小范围内进行搜索,以提高算法的收敛精度。仿真研究表明,论文的算法具有较高的收敛精度,并且解决局部极小问题也相当成功。
PSO算法; 遗传算法; 变异算子; 控制函数; 局部极小值
Class NumberTP301.6
1 引言
Kennedy J和Eberhart R于1995年提出了粒子群算法(PSO)[1]。作为一种快速仿生进化算法,PSO算法目前已广泛应用在工业领域中的优化问题[2]。本文称文献[1]提出的算法为基本PSO算法。基本PSO算法具有算法简单易用的优点,缺点是容易陷入优化问题的局部最优解。针对这个问题,人们对基本PSO算法进行了诸多改进,提出了不少改进的PSO算法。这些改进算法一般是对基本PSO算法的一些参数进行优化,难以解决基本PSO算法容易陷入局部最优解的矛盾[3~4]。遗传算法是一种全局搜索的优化算法,搜索的精度低。PSO算法的精度高,早期容易陷入局部最优解。PSO算法与遗传算法相结合的混合优化算法,能够利用遗传算法的全局搜索能力解决经典PSO算法容易陷入局部最优解的矛盾,同时也能解决遗传算法搜索精度低的问题。人们在这方面已经做出了不少工作[5~6]。文献[7]通过引进遗传操作的控制函数,在算法训练的早期主要由PSO算法进行搜索,在算法训练的后期遗传算法以接近于1的概率进行操作,避免算法陷入问题的局部解。
如上所述,PSO算法是一种局部优化“群智能”算法,通过种群内部粒子之间的竞争来搜索最优解,容易陷入局部最优解[8]。陷入局部最优解的原因是:在算法训练过程中,种群内部的粒子过早趋于一致,使得算法的搜索空间变得非常小。有效的解决方案是:在算法训练的前期,保持种群内部粒子的多样性,使得算法在解空间的较大范围内进行搜索;在算法训练的后期,缩小搜索范围,利用PSO的局部搜索能力向最优解方向进行搜索。这样能够避免PSO算法过早陷入局部最优解,同时也能够获得较高的收敛精度。
遗传算法是一种全局搜索的优化算法,缺陷是难以获得较高的收敛精度。遗传算法的全局搜索能力源于种群内部个体的多样性。在遗传算法训练过程中,算法主要通过变异操作和交叉操作保持种群内部个体的多样性,使得算法始终在解空间的较大范围内进行搜索。在采用实数编码时,操作变异算子更容易保持种群内部个体的多样性[9]。本文在经典PSO算法的基础上,通过一种变异算子控制函数,引入了遗传算法的变异算子。在算法训练的前期,变异算子采用比较大的变异率,以保持种群内部粒子的多样性,使得PSO算法能够在解空间的较大范围内进行搜索,以减小算法陷入局部最优解的概率;在训练的后期,变异算子采用比较小的变异率,使得PSO算法能够在解空间的较小范围内进行搜索,以提高算法的收敛精度。
2 基本PSO算法
考虑优化问题:f(x)是一个D维连续函数,优化问题为
minf(x)
X=[x1,x2,…,xD]s.t.xi∈[ai,bi]
(1)
其中:f(x)为目标函数,在PSO算法中称为适应度函数,[ai,bi]为xi搜索范围。设种群由N个粒子组成,每个粒子代表目标函数的一个候选解。Xi=(xi1,xi2,…,xiD)为第i个粒子在D维解空间的位置,Vi=(vi1,vi2,…,viD)为第i个粒子的速度,pbest=(pi1,pi2,…,piD)为第i个粒子当前最优位置,gbest=(pg1,pg2,…,pgD)为全体粒子当前最优位置[10]。则粒子根据式(2)和(3)来更新自己的速度和位置:
vid=w*vid+c1r1(pid-xid)+c2r2(pgd-xid)
(2)
xid=xid+vid
(3)
其中:c1和c2为学习因子,r1和r2为[0,1]范围内的均匀随机数,w为惯性系数[11]。根据经验,通常c1=c2=1.4962。i=1,2,…,D。对于惯性系数,本文采用动态递减的策略,将在下文给出具体的方案。
则基本PSO算法的步骤如下:
第一步:初始化,包括群体规模N,学习因子c1和c2,惯性系数w,每个粒子的位置xi和速度Vi,最大迭代次数epochmax;
第二步:对每个粒子,按式(1)计算其适应度值fit[i],并与其个体最优值pbest(i)比较,iffit[i]>pbest(i)thenpbest(i)=f[i];
第三步:寻找全局最优值gbest,即ifpbest(i)>gbest(i)thengbest=pbest(i);
第四步:根据式(2)、(3)更新粒子的速度vi和位置xi;
第五步如果满足结束条件,退出算法,否则返回第二步。
3 带遗传因子的PSO算法
基本PSO算法在算法训练的早期容易陷入局部最优解。为了解决这个问题,在上述PSO算法中引入了遗传算法的操作算子,以保持算法种群内部粒子的多样性,进而避免算法过早收敛到局部最优解。具体做法是引入一个变异算子控制函数,用来控制变异算子的变异率。在算法训练的前期,控制变异率取较大的值,以保持种群内部粒子的多样性,使得PSO算法在解空间的较大范围内进行搜索;在算法训练的后期,控制变异率取较小的值,根据PSO算法原理,此时种群内部的粒子很快趋于一致,使得PSO算法在解空间的较小范围内进行搜索。
变异控制函数如式(4)所示:
y(epoch)=(1-(epoch/epochmax)α)β
(4)
其中epoch表示当前迭代次数,epochmax表示最大迭代次数,α、β表示控制系数。图1是五组不同控制系数时控制函数的曲线,其中epochmax=3000,曲线1~曲线5的控制系数分别为(α,β)=(10,10)、(10,100)、(3,100)、(1.7,10)、(1.7,100)。如图1所示,通过设置适当的控制系数(α,β)可以使得:在算法迭代的前期,控制函数的值接近于1,在算法迭代的后期,控制函数的值非常小。

图1 五组不同控制系数时控制函数的曲线
根据式(4),变异算子的变异率由式(5)决定:
μ=m·y(epoch)
(5)
其中,μ是变异算子的变异率,m是预设变异率,设定后不变。
由式(4)和图1可以看出,当t∈[1,epochmax]时,控制函数y(epoch,α)是α的单调递增函数,y(epoch,β)是β的单调递减函数。这意味着,通过调节α和β的值,可以控制变异率μ相对迭代次数epoch的曲线。α越大,μ取较大值的迭代次数越多,β越大,μ取较小值的迭代次数越多。如前文所述,本文中的PSO算法要求在算法训练的前期,变异率取较大的值,在训练的后期,变异率取较小的值。因此,通过调节α和β的值,变异控制函数y(epoch)可以实现上述功能,并且可以实现变异率连续变化,而不是跳跃变化。
根据变异率,进行变异操作的粒子数由式(6)决定:
M=[N·μ]
(6)
其中M是进行变异操作的粒子数。
随机选择M个粒子进行变异操作,采用实数编码方案。考虑第k个粒子被选中进行变异操作,Xk=(xk1,xk2,…,xkD),其中第j个元素发生了变异,则操作策略为
xkj=xkj+rand·y(epoch)
(7)
其中rand∈(-a,a)是随机数。
由式(4)和式(7)可以看出,在算法训练的前期,变异后的粒子距离变异前的粒子比较远,变异后的粒子距离变异前的粒子比较近。对于算法也就意味着在训练的前期搜索空间相对比较大,减小了过早陷入局部最优解的概率;在训练的后期搜索空间相对比较小,能够集中资源向全局最优解方向搜索,以提高算法的收敛精度。
本文采用动态递减的惯性系数,动态惯性系数按式(8)计算
w=wmin+(wmax-wmin)y(epoch)
(8)
其中wmax表示最大惯性系数,wmin表示最小惯性系数。采用式(8)的目的是在算法训练的前期采用较大的惯性系数,算法能够在较大空间搜索;在算法训练的后期采用较小的惯性系数,算法能够在较小空间进行精细搜索。
算法的步骤如下:
第一步初始化,包括群体规模N,学习因子c1和c2,惯性系数w,每个粒子的位置xi和速度Vi,最大迭代次数epochmax,预设变异率m;
第二步按式(4)计算控制函数y(epoch),按式(8)计算惯性系数w;
第三步根据式(5)计算变异率,随机选择M个粒子按式(7)进行变异操作;
第四步对每个粒子,按式(1)计算其适应度值fit[i],并与其个体最优值pbest(i)比较,iffit[i]>pbest(i)thenpbest(i)=f[i];
第五步寻找全局最优值gbest,即ifpbest(i)>gbest(i)thengbest=pbest(i);
第六步根据式(2),式(3)更新粒子的速度vi和位置xi;
第七步如果满足结束条件,退出,否则返回第二步。
4 仿真研究
本文采用表1所示的函数对算法进行验证,其中f1(x)是单峰值函数,其他是多峰值函数,搜索空间是整个实数空间。
仿真1:以f2(x)为目标函数对算法进行仿真,图2~图3是仿真结果,仿真参数为(epochmax,N,α,β,wmin,wmax,c1,c2)=(3000,30,1.7,10,0.1,0.7298,1.4692,1.4692)。图2是种群中第一个粒子在解空间搜索的曲线,由图2不难看出,在算法迭代过程的前期,第一个粒子的搜索区间相对比较大;在算法迭代过程的后期,第一个粒子的搜索区间相对比较小。并且在算法训练的两个阶段,搜索区间的过渡比较平滑。这与图1中曲线4也基本吻合。
仿真2:以f2(x)为目标函数对算法进行仿真,仿真参数改变如下:α=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,2.0,5.0,10.0,20.0;β=10,20,50,100,200,共110组参数,每一组参数仿真100次,计算出最优性能指标的平均值,得图4所示一组曲线。由图可以看出,当参数α、β的值分别为1.7和10时,算法的收敛精度最高。
仿真3:分别以表1的函数为目标函数,参数N分别为20、30、40、50,其他参数与仿真1相同,每一组参数仿真100次,计算出最优性能指标的平均值,仿真结果如表2所示。通过与文献[2]的仿真结果比较可以看出,本文的算法的寻优性能整体上比较高。
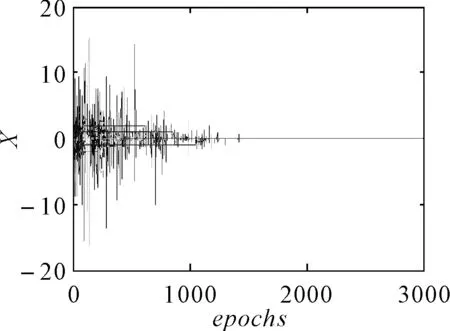
图2 粒子在解空间搜索曲线

图3 仿真1训练结果
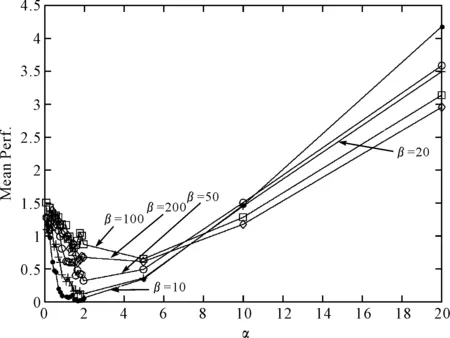
图4 目标函数f2(x)仿真结果

f1(x)f2(x)f3(x)f4(x)N=209.1341117e-240.63677385.6740390e-130.0003438N=301.5199802e-330.08954635.6843419e-140N=401.4920326e-420.03979834.5723425e-140N=504.0368056e-490.01989924.0785153e-140
5 结语
本文在基本PSO算法基础上,引入了遗传算法的变异算子。通过变异算子的控制函数,将PSO算法的训练过程分为前期和后期。在算法训练的前期,变异算子采用比较大的变异率,以保持种群内部粒子的多样性,使得PSO算法能够在解空间的较大范围内进行搜索,以减小算法陷入局部最优解的概率;在训练的后期,变异算子采用比较小的变异率,使得PSO算法能够在解空间的较小范围内进行搜索,以提高算法的收敛精度。仿真研究表明,本文的算法具有较高的收敛精度,并且解决局部极小问题也相当成功。
[1] Kennedy J, Eberhart R C.Particle swarm optimization [C]//Perth: Proceedings of the 4th IEEE International Conference on Neural Networks,1995:1942-1948.
[2] 高浩,冷文浩,须文波.一种全局收敛的PSO算法及其收敛分析[J].控制与决策,2009(2):196-201.
[3] Kalyan Veeramachneni,Lisa O,Ganapathi K.Probabilistically driven particle swarms for optiomization of multi valued discrete problems:Design an analysis[C]//Honolulu: Proc of IEEE Swarm Intelligence Symposium (SIS),2007:141-149.
[4] Paul S Andrew.An investigation into mutation operators for particle swarm optimization[J].IEEE Congress on Evolutionary Computation,Vancouver,2006,16(21):1044-1051.
[5] 范晋伟,梅钦,李海涌,等.PSO-GA组合算法优化PID参数及可视化平台设计[J].机械设计与制造,2013(8):8-11.
[6] M.Senthil A,M.V.C.Rao,Aarthi C.A new improved version of particle swarm optimization algorithm with global-local best parameters[J].Knowledge and Information Systems,2008,16(3):331-357.
[7] Gandelli A,Grimaccia F,Mussetta,et al.Development and validation of different hybridization strategies between GA and PSO[J].IEEE Congress on Evolutionary Computation,2007,25(28):2782-2785.
[8] Dong Hwa Kim, Kaoro Hirota.Vector control for loss minimization of induction motor using GA-PSO[J].Applied Soft Computing 8,2008:1692-1702.
[9] 李勇,吴敏,曹卫华,等.基于线性规划和遗传—粒子群算法的烧结配料多目标综合优化方法[J].控制理论与应用,2011(12):1740-1746.
[10] 周建新.基于GA-PSO的区域人力资本预测模型研究[D].成都:成都理工大学:2009:15-16.
[11] Hui Liu, Hong-qi Tian, Chao Chen, Yan-fei Li.An experimental investigation of two Wavelet-MLP hybrid frameworks[J].Electrical Power and Energy Systems,2013,52:161-173.
A PSO Algorithm with Mutation Operator
YU RenboZHAO XiupingMENG Fanlei
(Department of Airborne Vehicle Engineering, Naval Aeronautical and Astronautical University, Yantai264001)
In this paper, the mutation operator, which is used in Genetic Algorithm, is introduced into the basical PSO algorithm. By mutation operator control function, the training process of the PSO algorithm is divided into early phase and late phase. In the early phase of the algorithm train, the mutation rate is larger, so the more particles are chosen to take the mutation operation, in order to enhance the diversity of the population’s particles, and the PSO algorithm can hunt in a large solution space to avoid being trapped in the local optimal solution too early. In the late phase of the algorithm train, the mutation rate is smaller, so the less particles are chosen to take the mutation operation, in order to attenuate the diversity of the population’s particles, therefore the PSO algorithm can hunt in a smaller solution space to improve the convergence accuracy of the algorithm. Simulation results show that, the convergence precision of this algorithm is higher, and solution of the local minimum problem is quite well.
PSO algorithm, genetic algorithm, mutation operator, control function, local minimum
2016年4月17日,
2016年5月31日
余仁波,男,讲师,研究方向:兵器发射理论与技术、装备综合保障理论与技术。赵修平,男,教授,研究方向:兵器发射理论与技术。孟凡磊,男,讲师,研究方向:兵器发射理论与技术。
TP301.6
10.3969/j.issn.1672-9730.2016.10.008

