基于滑移网格的带桨水面船自航性能预报研究

祝启波，王志东，凌宏杰，庄丽帆

（江苏科技大学 船舶与海洋工程学院，江苏　镇江 212003）

基于滑移网格的带桨水面船自航性能预报研究

祝启波，王志东，凌宏杰，庄丽帆

（江苏科技大学 船舶与海洋工程学院，江苏镇江 212003）

应用 FINE/Marine 软件对 KCS 船、KP505 桨以及考虑自由液面的船桨组合体进行数值计算，并计算其自航性能。利用滑移网格技术和随体网格来实现船桨之间的相互耦合。考虑到原有的自航性能数据处理方法并不代表实际情况，文中借鉴强制自航法的概念提出了一种新的船舶自航点求解方法预报船舶自航性能，并与模型试验结果进行比较，吻合良好，其中推力减额系数、伴流分数以及船舶推进效率的计算误差分别为0.5%、2.18%、6.76%。本文研究为预报船舶自航性能提供了一种新的研究手段。

KCS；数值模拟；滑移网格；船舶自航

0　引　言

随着国际船级社协会（IACS）制定了新的造船标准，高效、节能成为业内关注的方向，深入开展船/桨相互作用下的船舶自航性能研究对于改进船型、优化附体设计和改善推进性能具有重要作用。相比于传统模型试验受到实验设备及其他因素的制约，应用 CFD技术开展船舶自航性能研究具有较明显的优势。

应用 CFD 方法预报船模自航性能，需要开展船模阻力、螺旋桨敞水和船模自航的数值计算；每个步骤的计算误差都会对自航性能的预报产生影响，因此为使预报结果达到工程实用的要求，对每一环节的计算精度都应有一定的要求。目前，有关船模阻力和螺旋桨敞水性能的研究已有很多，并达到较高精度；而船舶自航 CFD 模拟需要对船-桨-舵系统整体求解，问题较为复杂。因此，基于 CFD 模拟的船舶自航性能预报，其难点在于自航模拟中如何处理船桨之间的相互耦合。

目前研究船桨干扰的数值方法基本上可以分为整体建模法和体积力法两类［1-4］。这2种方法各有优劣，桨实体建模计算效率较力场法低，但预报的信息更为全面。自航性能 CFD 研究需实现螺旋桨与船体的整体求解，而在船桨整体建模计算时，船桨处理又可分为MRF 法、混合面法和滑移面法［5］3种，其中滑移网格法能模拟船桨干扰的非稳态效应，得到非稳态解，因而应用更加广泛。在国内，张志荣［6］等较早开展了基于 CFD 方法的船桨干扰研究，采用 MRF和滑移网格法对船桨干扰进行计算；沈海龙［7］等应用 DES 湍流模型及滑移网格法对船桨干扰进行计算；刘祥珺［8］通过滑移网格技术，同时考虑自由液面、真实螺旋桨的旋转运动，实现了船-桨的整体数值计算，模仿物理水池自航试验，计算了伴流系数与自航因子等参数。

强制自航法是指船模在螺旋桨推力和强制力的共同作用下进行的自航试验，其中强制力是指，由于船摸与实船两者的 Re 不相等，两者的摩擦阻力不存在 λ3的关系，为克服这个矛盾需对摩擦阻力修正，其修正值 SFC 即为强制力。本文在总结以往研究的基础上，借鉴强制自航法，通过对模型尺寸下的 KCS 船模加入强制力来满足相似定律，使船模在螺旋桨推力和强制力的共同作用下进行自航，通过改变螺旋桨转速得到不同的船模航速，利用插值方法得到船舶实际自航点，从而实现船舶自航性能的数值预报。

1　数值计算方法及研究对象

1.1控制方程及离散格式

控制方程由连续方程、运动方程和能量方程组成，在实际过程中水和空气都作为不可压缩流体来考虑，只需考虑连续方程和运动方程，即满足下式：

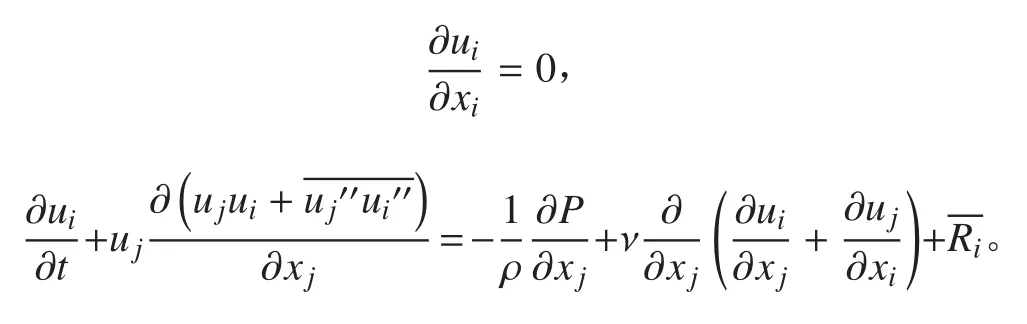
式中 ui，uj，p 为时均值。

本文 CFD 计算采用剪切压力传输（SST）k-ω 模型，其结合之前 k-ω 模型的优点，能够计算流动分离的区域。对于动量方程和湍流方程，本文均采用AVLSMART 格式进行离散，对于自由液面运动方程采用 BRICS 格式，可压缩性 BRICS 离散格式可有效减小自由液面模拟的数值耗散误差。

1.2研究对象

以 KRISO 的 3600TEU 集装箱船模 KCS 为研究对象，其螺旋桨为KP505，作为国际通用的标准船型，设计航速为24 kn，尾部流场特征比较明显，有大量试验和数值计算结果，为对比计算结果提供了方便。船模及其桨的主要参数见表1和表2，KCS 船的模型缩尺比为31.6。图1为KCS船型计算模型，图2为船桨组合计算模型。

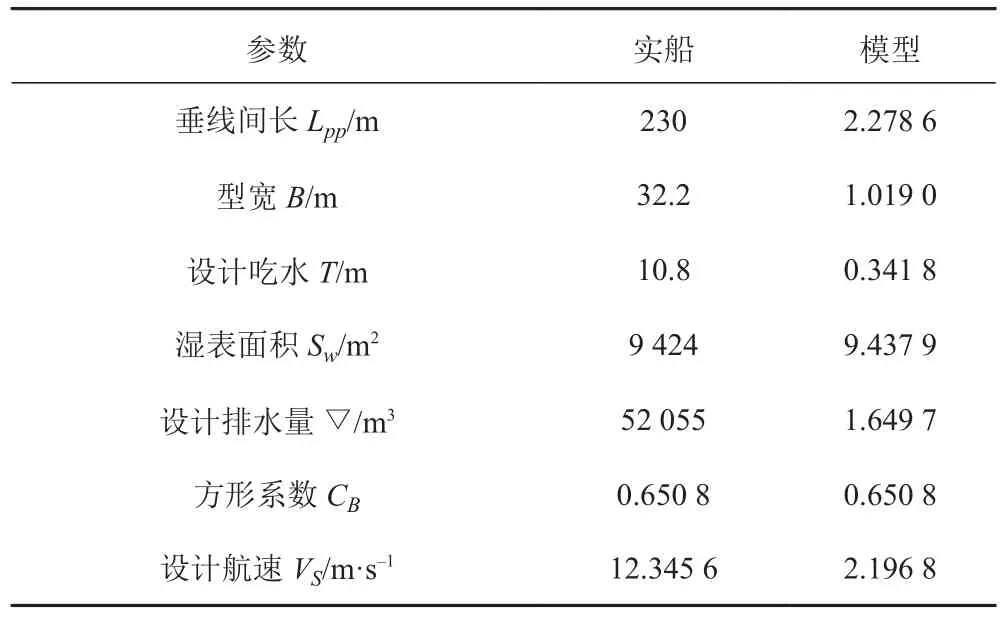
表1　KCS 实船及模型主要参数Tab. 1　Main dimensions of KCS model

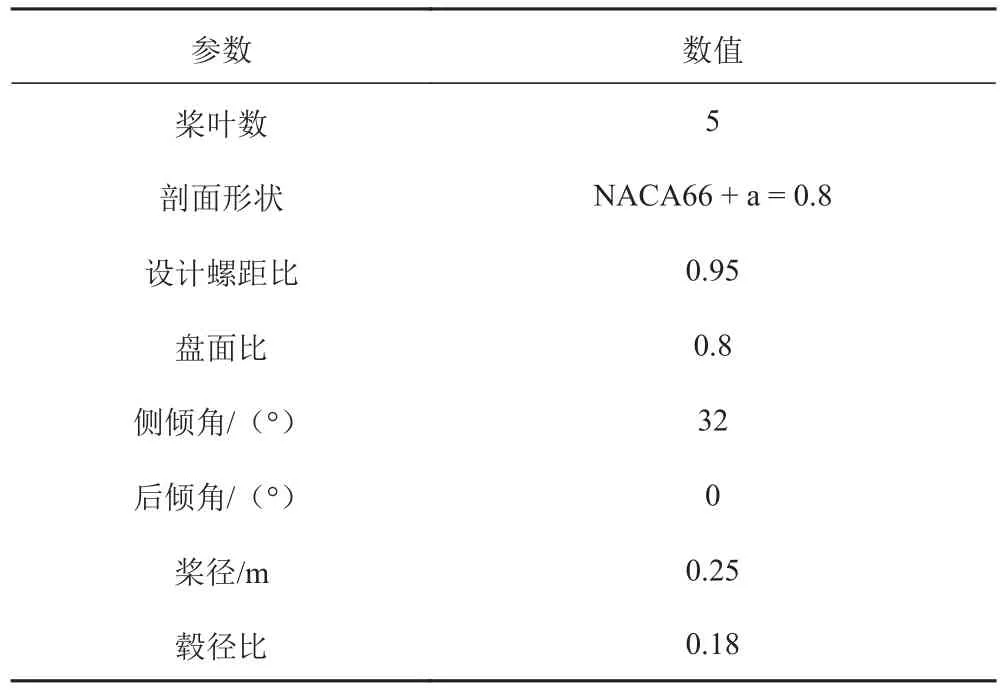
表2　KP505 螺旋桨模型主要参数Tab. 2　Main dimensions of KP505

图1　KCS 船型计算模型Fig. 1　KCS ship computational model

图2　KCS 船桨组合计算模型Fig. 2　KCS ship and propeller computational model

计算原点坐标位于艉垂线与船底中心线的交点处。x 轴为中纵剖面和船底面的交线，正方向指向船首；y 轴正方向指向船体左舷；z 轴正方向向上。

1.3网格划分与边界条件

计算中使用的网格为全六面体非结构网格，通过在物面上适当细化并投影，从而形成贴体网格，实现物体外形的准确描述。

对于船模阻力计算，计算域进口位于模型首部前方约 1.2 Lpp处，出口边界位于模型尾部后方约3 Lpp处，左右边界到船模侧面的距离约为1.8 Lpp处，上边界位于水线以上 0.5 Lpp处，下边界位于水线以下2 Lpp处。船模阻力的网格单元总数约为108 万，船模表面网格划分如图3所示。

图3　船模表面网格划分Fig. 3　Meshing of hull

对于螺旋桨敞水计算，其计算域分为外域及桨域，两者通过滑移网格实现信息交换。外域为一长方体，桨域为一以桨轴中心线为轴的圆柱体，桨域入流面位于桨盘面上游 0.3 R 处，桨域出流面位于桨盘面下游 0.3 R 处，圆柱体外径为1.2 R。计算域网格单元总数约为170 万，其中桨域网格单元数约为50 万，图4为螺旋桨桨域的网格划分。

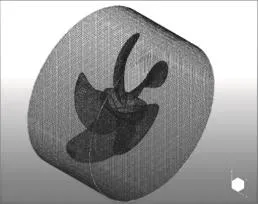
图4　螺旋桨桨域网格划分Fig. 4　Meshing of propeller

船模阻力和螺旋桨敞水边界条件设置：进口处选用入流条件，给定来流速度，出口选用零压力梯度条件，出口处的压力与前方某一点的压力始终一致；左右表面选用速度远场，船体及螺旋桨表面引入标准壁函数，以均匀来流作为计算初始条件。

对于船模自航计算，其计算域的设定与裸船阻力数值计算有一定的相似性，如图5所示。整个流动区域划分为船桨2个子域，桨域设在船舶尾部螺旋桨区域，如图6所示，船域与桨域之间采用滑移网格模型，来实现交界面处流动信息的传递。计算域的网格单元总数约为250 万，其中桨域的网格单元数约为120 万。

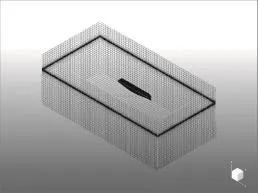
图5　带桨水面船计算区域与网格划分Fig. 5　Meshing of computational domain

图6　船域与桨域之间网格划分Fig. 6　Meshing of propeller domain

船模自航模拟边界条件设置：进口处选用速度远场，出口选用零压力梯度条件，出口处的压力与前方某一点的压力始终一致；左右表面选用速度远场，船体及螺旋桨表面引入标准壁函数，给定螺旋桨一定转速作为计算初始条件。

2　船模自航点求解方法

目前，许多学者采用类似模型试验即等车速变转速的方法来计算船模的自航点，即在某一航速 V 下通过改变螺旋桨转速 n 可得到推力 T 随 n 的变化曲线和（Rt（sp）-SFC）随 n 的变化曲线，两曲线的交点即为该航速下的实船自航点。但这种方法并不是螺旋桨产生推力使得船舶向前航行，未能实现船舶与螺旋桨之间的真正耦合。

本文在研究船模自航性能时，仅给予螺旋桨一定转速，由螺旋桨产生推力带动船体向前航行，真正意义上实现了水面船舶自航的数值模拟。

基于上述情况，本文给出一种新的研究方法来预报实船自航性能。具体研究方法如下：

1）根据船舶航速及自身特点，一定范围内预估几个自航转速（n1，n2，n3，…），应该保证实际自航点在所选的范围之中。

2）根据船型特点，计算出目标航速 Vm下的船舶摩擦阻力修正值，在计算时作为强制力Z施加到船体上，使得螺旋桨产生的推力只需要克服（Rt（sp）-SFC）。

3）进行各转速下船舶自航数值模拟，计算过程中船体在螺旋桨产生的推力和强制力Z作用下向前航行。根据数值模拟结果，可以得到船舶航速 V，桨推力 T、船阻力 RT（SP）、桨扭矩 QPROP和船扭矩QHULL，并绘制相应曲线。

4）绘制船舶航速 V 随桨转速 n 的变化曲线，并由u=Vm插值求得自航点转速 nm，如图7所示。

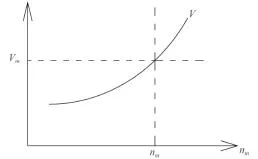
图7　自航转速曲线Fig. 7　Curve of self-propulsion speed

5）根据自航点转速 Nm结合船体阻力试验以及螺旋桨敞水特性曲线，可以得到船模的实效自航性能。

3　计算结果与分析

为预报船模自航性能，本文先对船模阻力、螺旋桨敞水进行数值计算，然后对船桨整体进行自航模拟。

3.1船模阻力数值计算

首先对考虑自由液面的船体阻力进行数值模拟，数值计算得到的船模阻力与阻力系数列见表3，表中同时给出了模型试验结果，其中模型试验的摩擦阻力系数由 1957-ITTC 公式计算求得。从表中可看出，该工况下数值计算的阻力及阻力系数与模型试验结果吻合良好，相对偏差均小于 5%。

图8为裸船体周围波高等高线分布。

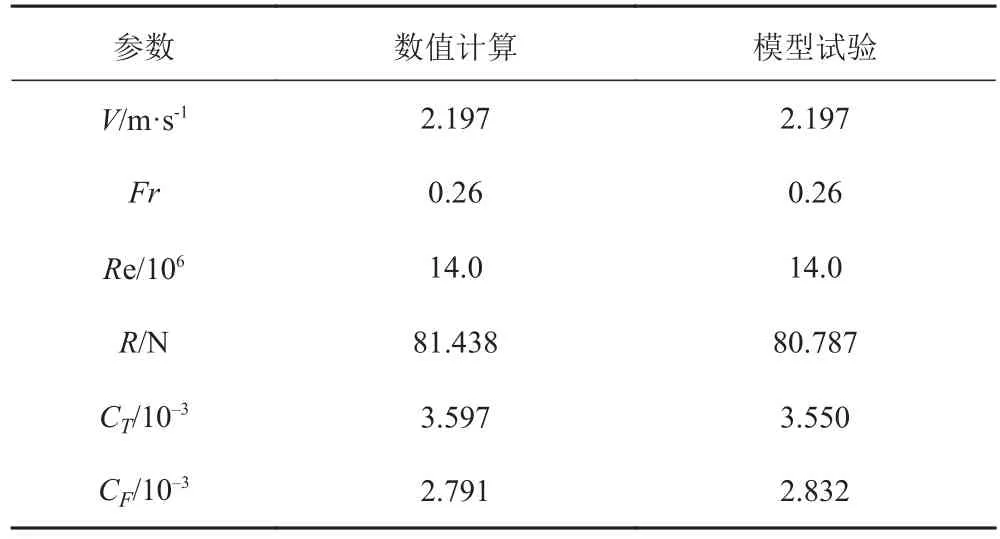
表3　KCS 船模阻力/阻力系数计算结果Tab. 3　Resistance/resistance coefficients of KCS

图8　裸船体周围波高等高线分布图Fig. 8　Comparison of the wave contour near the ship

3.2螺旋桨敞水数值计算

选取进速系数 J 从 0.1 到 0.9 进行计算，共9种工况，图9给出了计算所得到的螺旋桨敞水性能曲线与试验曲线的比较，图中的 KT，KQ及 η 的试验值均由Gothenburg2000 会议所提供。计算结果与试验值吻合良；对于进速系数，高进速工况下计算所得的推力偏小，预报效果略差；对于扭矩系数，误差在 4% 以内，而对于敞水效率，进速系数 J 在 0.3～0.8 内预报精度较高，误差在 3% 以内。计算所得的推力系数、扭矩系数和螺旋桨敞水效率误差在 5% 以内，满足工程精度的要求。

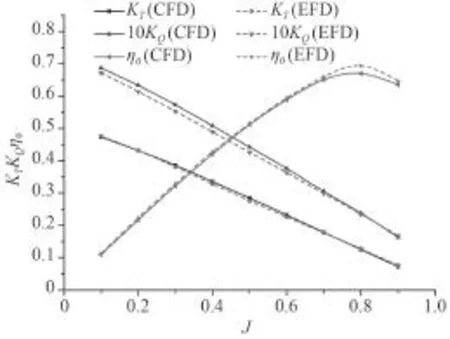
图9　KP505 螺旋桨敞水性能曲线（计算与试验）Fig. 9　Comparison of open water performance of KP505（CFD and EFD）

3.3船模自航数值计算

本文船模的自航速度 U=2.196 8 m/s，参考以前的数值模拟经验，选取3个不同的螺旋桨转速 N1=9.5 r/s，N2=9.6 r/s，N3=9.7 r/s 作为数值计算自航点的参考转速，分别对这3个转速进行自航数值模拟，计算得到各转速下船模的航速 V、桨推力T、船阻力 RT（SP）、桨扭矩 QPROP和船扭矩 QHULL，如图10～图12所示，其值列于表4。由图中看出：本文成功模拟了船模从启动到稳定自航运动的过程；在 t=0.5 s 之前桨推力随着转速的增大不断增大，t=0.5 s 后随着进速的增大不断减小；随着船速的增大，船阻力不断增大；在 t=80 s后船舶速度达到稳定。

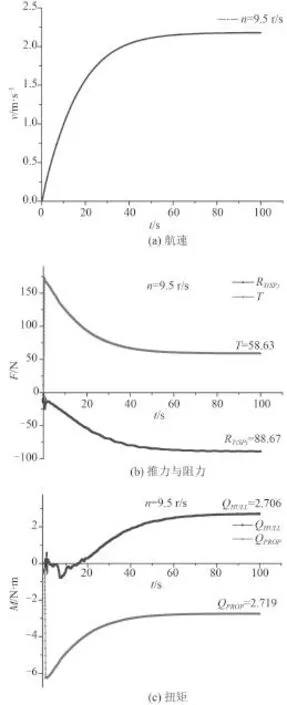
图10　n=9.5 r/s 船模的航速 V、桨推力 T、船阻力 RT（SP）、桨扭矩 QPROP和船扭矩 QHULLFig. 10　n=9.5 r/s Ship speed V， propeller thrust T， ship resistance RT（SP）， propeller torque QPROPand ship torque QHULL

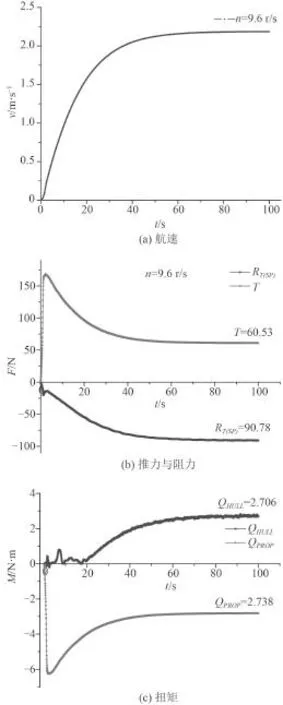
图11　n=9.6 r/s 船模的航速 V、桨推力 T、船阻力 RT（SP）、桨扭矩 QPROP和船扭矩 QHULLFig. 11　n=9.6 r/s Ship speed V， propeller thrust T， ship resistance RT（SP）， propeller torque QPROPand ship torque QHULL

由表4绘制的航速-转速曲线如图13所示，通过插值求得 U=2.196 8 m/s 的转速 n=9.662 5 r/s；再由数值试验自航曲线（见图14）插值求得 T=61.63 N，KT=0.169，Q=2.754 N·m，10KQ=0.302。

根据 KT0=KT，在螺旋桨敞水特性曲线上通过插值求得 J0=0.720，10KQ0=0.303，η0=0.657。则船模的实际伴流分数 ωm=0.209，相对旋转效率 ηR=1.003。船桨自航计算结果列于表5，从表中可以看出，数值模拟结果与试验结果吻合良好，基本满足工程精度的要求。由表5可见船桨自航时螺旋桨敞水效率 η0、相对旋转效率 ηR和船身效率 ηH均小于试验值，因此推进效率 ηD误差较大，达到 6.76%。

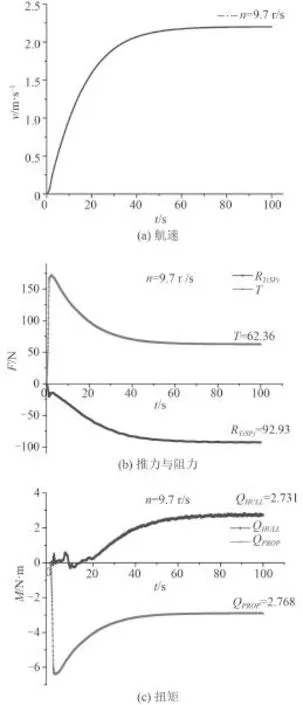
图12　n=9.7 r/s 船模的航速 V、桨推力 T、船阻力 RT（SP）、桨扭矩 QPROP和船扭矩 QHULLFig. 12　n=9.7 r/s Ship speed V， propeller thrust T， ship resistance RT（SP）， propeller torque QPROPand ship torque QHULL

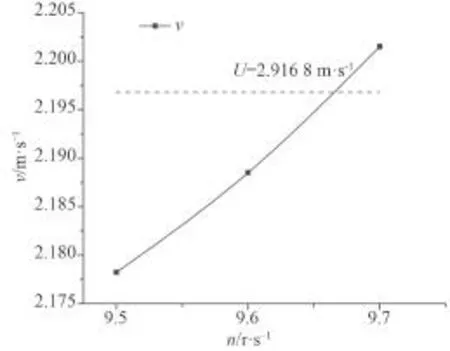
图13　航速-转速曲线Fig. 13　Curve of V-n

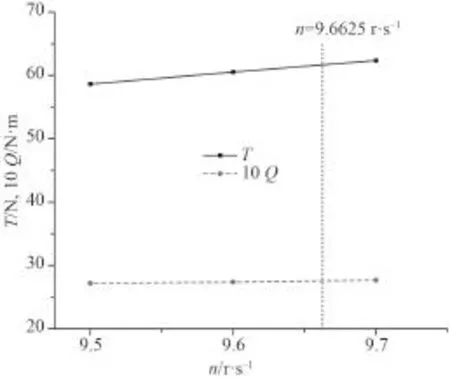
图14　数值试验自航曲线Fig. 14　Computational results of self-propulsion

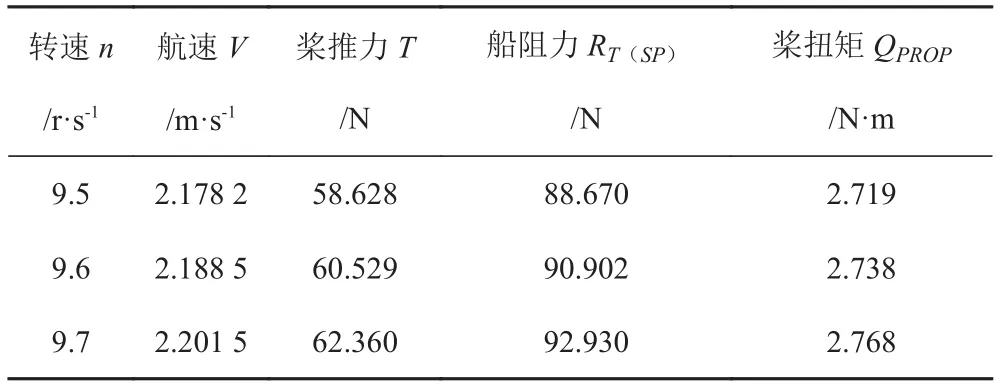
表4　数值自航结果Tab. 4　Computational results of self-propulsion

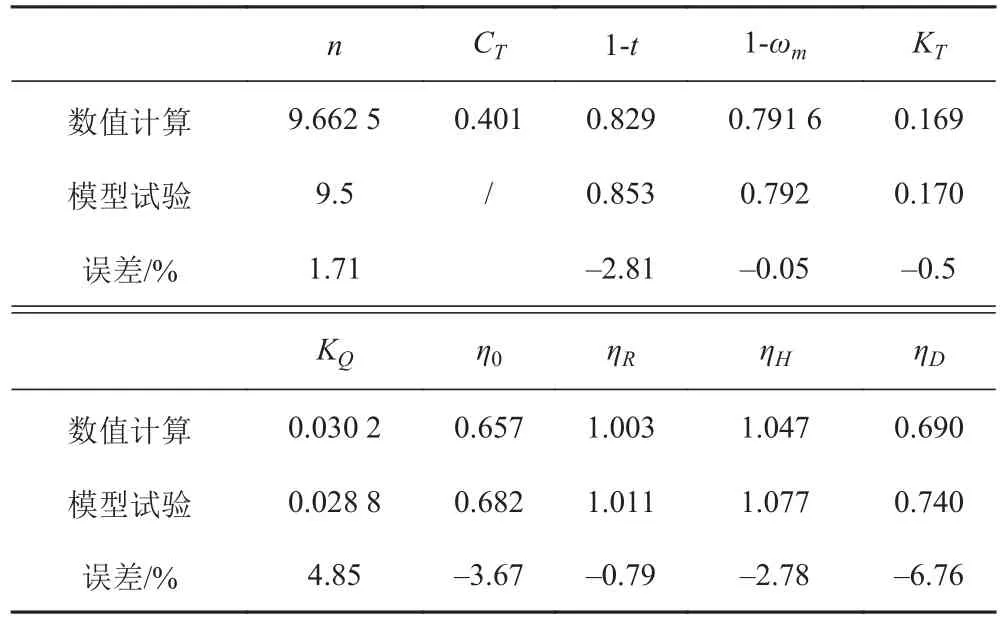
表5　船桨自航计算结果Tab. 5　Computational results of self-propulsion with propeller

图15为带桨及不带桨时船尾压力分布对比图，其中不带桨选取的是船航速为2.196 8 m/s 的工况，而带桨选取的是最靠近自航点转速的计算工况（n=9.7 r/s）。从图中可以明显看出：带桨时船尾部零压力线较不带桨时其位置发生了后移，这是由于螺旋桨在船尾的抽吸作用，使得整个船尾部区域的压力降低，导致船尾部压力分布的变化；不带桨时船桨连接处的压力均为正压，而螺旋桨在船后工作时部分船桨连接处出现了负压；不带桨及带桨时船尾压力分布对比图反映了螺旋桨对于船体的影响。

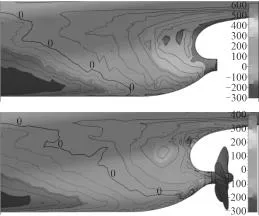
图15　带桨及不带桨船体尾部压力对比（上图为不带桨、下图为带桨）Fig. 15　Comparison of hull stern pressure with and without propeller（up is without propeller， below is with propeller）

4　结　语

本文应用 FINE/Marine 软件对船模阻力、螺旋桨敞水和船模自航进行数值计算，将所得计算结果与试验数据进行比较，吻合良好。对于裸船阻力的数值模拟，总阻力系数比试验值大 1.32%，对于螺旋桨敞水性能，推力系数和扭矩系数相比于试验值误差均在 5%以内，在研究船舶自航性能中，数值计算的船舶推进效率比试验值小 6.76%，计算结果基本满足工程实用的要求。由于船体是通过螺旋桨产生推力向前航行，本文采用的计算方法与实际情况更为接近：同时该方法模拟了船舶从启动到稳定航行的过程。基于上述计算方法，本文提出了一种新的实际自航点确定方法，并获得了目标船舶的自航性能。数值计算结果表明该研究方法能够提高船舶自航性能的预报精度。

8（3）： 182-191.

［1］CHEN H C， CHEN M M. Chimera RANS simulation of a berthing DDG-51 ship in translational and rotational motions［J］. International Journal of Offshore and Polar Engineering， 1998，8（3）： 182-191.

［2］CHOU S K， CHAU S W， CHEN W C， et al. Computations of ship flow around commercial hull forms with free surface or propeller effects［C］//Proceedings of the Workshop on Numerical Ship Hydrodynamics. Gothenburg， Sweden， 2000.

［3］KIMURA K， TAKETANI T， YAMASAKI E， et al. Study on interaction between ship hull and propeller using RANS method with VLM［C］//Proceedings of the 7th International Conference on Hydrodynamics. Ischia， Italy： ICHD， 2006.

［4］吴召华. 基于体积力法的船-桨-舵粘性流场的所数值研究［D］.上海： 上海交通大学， 2013. WU Zhao-hua. Numerical study of viscous flow around ship hull/propeller/rudder with a body-force propeller［D］. Shanghai：Shanghai Jiaotong University， 2013.

［5］姚震球， 高慧， 杨春蕾. 基于滑移网格的带螺旋桨艇体尾流场数值分析方法［J］. 江苏科技大学学报（自然科学版）， 2008，22（2）： 15-20. YAO Zhen-qiu， GAO Hui， YANG Chun-lei. Numerical simulation of interaction between submarine and propeller based on approach of sliding mesh［J］. Journal of Jiangsu University of Science and Technology （Natural Science Edition）， 2008， 22（2）：15-20.

［6］张志荣， 李百齐， 赵峰. 螺旋桨/船体粘性流场的整体数值求解［J］. 船舶力学， 2004， 8（5）： 19-26. ZHANG Zhi-rong， LI Bai-qi， ZHAO Feng. Integral calculation of viscous flow around ship hull with propeller［J］. Journal of Ship Mechanics， 2004， 8（5）： 19-26.

［7］沈海龙， 苏玉民. 基于滑移网格技术的船桨相互干扰研究［J］.哈尔滨工程大学学报， 2010， 31（1）： 1-7. SHEN Hai-long， SU Yu-min. Use of the sliding mesh technique to analyze interaction between ship hulls and propellers［J］. Journal of Harbin Engineering University， 2010， 31（1）： 1-7.

［8］刘祥珺， 孙存楼. 数值水池船模自航试验研究方法［J］. 舰船科学技术， 2011， 33（2）： 28-31. LIU Xiang-jun， SUN Cun-lou. Research on ship self-propulsion model test in numerical tank［J］. Ship Science and Technology，2011， 33（2）： 28-31.

Use of the sliding mesh technique to forecast ship self-propulsion performance with propeller in open water

ZHU Qi-bo， WANG Zhi-dong， LING Hong-jie， ZHUANG Li-fan
（Department of Naval Architecture and Ocean Engineering， Jiangsu University of Science and Technology，Zhenjiang 212003， China）

Numerical simulations are performed for KCS， propeller KP505， KCS/KP505 inter-action considered the free surface by using the software FINE/Marine， and the ship self-propulsion performance are forecasted. The hull/propeller interaction are carried by sliding mesh and mesh with body technique. The original numerical simulation method can't represent actual situation， this paper proposes a new method to forecast ship self-propulsion from the concept of English me-thod of self-propulsion test. The result showed that the numerical simulation matched well with the model test measurement， the error for thrust deduction fraction， wake fraction and ship propul-sion is around 0.5， 2.18 and 6.67%. This study provided a new method to forecast the ship self-pro-pulsion performance.

KCS；numerical simulation；sliding mesh technique；ship self-propulsion

U661.31

A

1672-7619（2016）09-0042-07

10.3404/j.issn.1672-7619.2016.09.008

2016-01-15；

2016-02-29

祝启波（1990-），男，硕士研究生，研究方向为流体力学。