基于多重自由设站在基坑沉降监测中的研究

罗伯成　吴海科

(贵州大学土木工程学院，贵州 贵阳　550025)



基于多重自由设站在基坑沉降监测中的研究

罗伯成吴海科

(贵州大学土木工程学院，贵州 贵阳550025)

介绍了全站仪三角高程测量的原理，并以茅台4号大桥古蔺岸工程为例，对全站仪测量位移和沉降精度进行了分析，通过分析结果，选择了相应的测量仪器，达到了实时、快速和准确反映基坑沉降的目的。

复杂基坑，多重自由设站，沉降监测，监测点

0　引言

在多山地区的基坑监测中，基坑周围工作面较为狭窄、基坑开挖形状不规则，采用常规的监测方法往往无法对基坑沉降进行实时监测。为此，我们可以采用在基坑附近自由设站的方法进行监测[1,2]。但以往测量的科研工作者在布置自由设站点时都只有一个或几个相互独立的自由设站点，由于开挖基坑和施工场地的特殊性，以上自由设站的方法无法覆盖整个监测网。为了对整个基坑进行实时监测，在此提出基于多重自由设站的方法对基坑进行沉降监测，也就是为了建立能够对基坑所有监测点进行监测，采用多个连续自由设站的方法对基坑进行监测。下面就贵州省茅台4号大桥古蔺岸为例来阐述深基坑监测测站点的布置方法的优化。

茅台4号大桥位于贵州省遵义市茅台镇茅台酒厂附近，交通方便，桥位横跨赤水河。由于该桥为人行悬索，为保护当地的自然环境，不允许为了施工和监测的需要而大量破坏基坑周围的自然环境，这就导致监测场地往往较为狭窄。随着智能型全站仪的应用和普及，采用全站仪随架随测的多重自由设站法能有效解决以上监测的困难。

1　全站仪自由设站

1.1全站仪计算坐标的原理

全站仪可以测量测站点与监测点之间的斜距S以及直接测量出监测点相对于测站点的垂直角β，进而全站仪自带的程序将自动计算出待测点的坐标[3]，其高差计算公式为：ΔH=Ssinβ，其计算理论原理如下：

z监测点=z测站点+i+Ssinβ-v

(1)

其中，z监测点，z测站点分别为监测点和测站点的高程坐标；i为仪器高；v为棱镜高。

1.2全站仪多重自由设站观测原理

全站仪自由设站法观测，它是一种以角度与距离同时测量的极坐标法为基础，应用自动化高精度全站仪在基坑附近一方便观测的位置设一观测站，随意设置测站点的坐标及任一个方向的方位角进行定向，将其中一个基准点作为后视点，利用全站仪的自动监测功能采用极坐标的方法对每个监测点进行观测，这样实际上就是建立了一个自由坐标系，每次都利用其中一个基准点作为测站点，另一个基准点作为后视点，对自由设站的测站点进行监测，进而得到其坐标，然后从观测站上观测若干个已知基准点及变形监测点的方向和距离。当联测这几个基准点时，基准点就有了自由坐标系和统一坐标系中的两套坐标数据。全站仪内置的自由设站观测程序就可以利用这些基准点将所有点(包括测站点)的自由坐标转换为统一坐标，通过对各点的周期性观测，便可得到各变形观测点的位移变化[4]。

2　全站仪测量位移和沉降精度估算

2.1监测点的点位误差

将式(1)全微分，再根据误差传播定律[5]，可得监测点的坐标误差：

(2)

其中,mS，mβ，mi,mv分别为全站仪测量斜距的中误差、垂直角的中误差、仪器高中误差、棱镜高中误差。

2.2球气差：由地球曲率和大气折光引起的误差

高程的测量受地球曲率c和大气折光r的影响，其中：

则有：

(3)

将式(3)全微分，再根据误差传播定律，可得球气差引起的误差：

mc-r=

(4)

其中，mK为大气折光系数误差[6]。

根据已有的实验证明，当S<1 000 m时，大气折光系数K在我国约为0.08～0.14，大气折光系数误差mK为±(0.3～0.5)[7]。在桥梁监测中，斜距一般不会很大，所以若斜距S≤300 m时，mc-r≈0，所以球气差的影响可以忽略不计。

2.3仪器对中误差、监测点偏心误差、仪器高中误差和棱镜高中误差

全站仪对中是采用仪器自带的激光对中器或光学对中器，根据大量的现场实际经验，当对中器和照准部水准器进行严格的检验校正后，仪器对中误差在±1 mm内；当监测点采用三脚架和棱镜基座安置棱镜时，其偏心误差和棱镜高中误差在±1 mm内，有m仪器对中=m偏心=mv=±1 mm[8]。

当建立具有稳定的观测墩和具有强制对中装置的棱镜台，那么仪器对中误差和监测点偏心误差以及棱镜高中误差都很小，可以不予考虑，即m仪器对中=m偏心=mv=0 mm[8]；在仪高测量中，采用游标卡尺在基座三个方向量取，使三个方向量取的校差小于0.2 mm，并在测前、测后进行两次量测，使mi=0.2 mm，以此减少仪高测量的误差[9]。

2.4多重自由设站时监测点沉降的点位中误差

在应用全站仪测量坐标时，由于仪器的监测点的点位误差、由地球曲率和大气折光引起的误差、仪器对中误差、监测点偏心误差、仪器高中误差和棱镜高中误差之间相互独立，因此根据误差传播定律，第一个自由设站点(自由设站点1)沉降的点位中误差为：

(5)

其中，S1，i1，β1，v1，m仪器对中1，m偏心1分别为测量第一个自由设站时的斜距、仪高、垂直角、棱镜高、仪器对中误差、偏心误差。

同理，根据误差传播定律，第二个自由设站点(自由设站点2)沉降的点位中误差为：

(6)

其中，S2，i2，β2，v2，m仪器对中2，m偏心2分别为测量第二个自由设站时的斜距、仪高、垂直角、棱镜高、仪器对中误差、偏心误差。

同理，监测点沉降的点位中误差为：

(7)

其中，S3，i3，β3，v3，m仪器对中3，m偏心3分别为测量第三个自由设站时的斜距、仪高、垂直角、棱镜高、仪器对中误差、偏心误差。

同理可以推导多重自由设站沉降的点位中误差公式。

3　复杂基坑自由设站点和监测点的布置实例分析

3.1基坑自由设站点和监测点布置概况

茅台4号大桥古蔺岸为扩大基础，基坑最大深度达到22 m。其现场施工图如图1所示。

从图1可以看出，基坑周围地形起伏很大，且有大量绿化植物。由于在稳定区域无法找到可以通视全部监测点的基准点，所以采用常规的方法无法对基坑的沉降进行监测。但在西侧的房屋处有一处相对空旷场地，为此可以在房屋处布置两个基准点1和基准点2，在基坑旁布置自由设站点1。但即便如此，利用基准点1也无法监测整个基坑，所以在自由设站点1的基础上建立自由设站点2，这样就建立了二重自由设站(两个连续自由设站)，其设站和监测点布置图如图2所示。

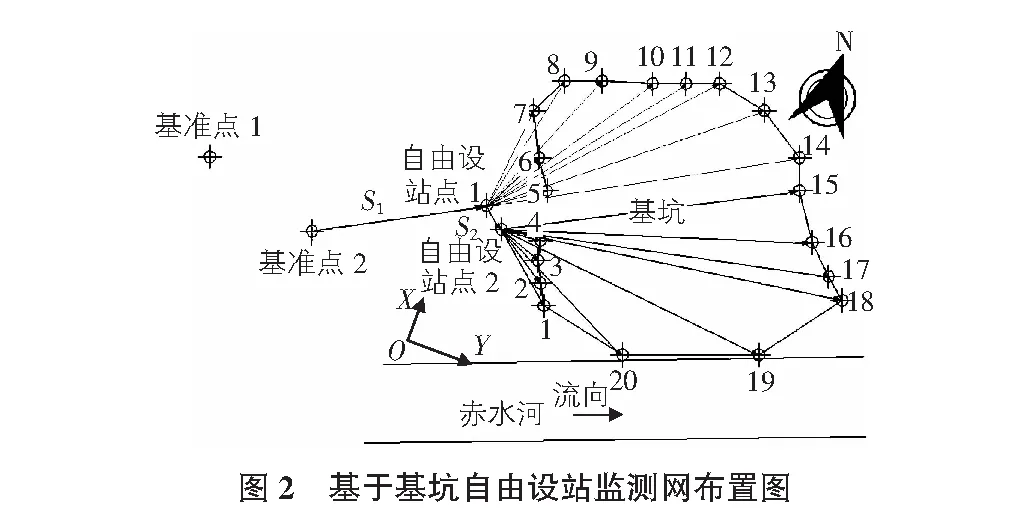
如图2所示，为了能够更加清楚的反映基坑的变形，对监测点的布置进行适当的加密。基准点1，点2布置于稳定区域，由于工程周边地形的复杂与特殊性，本次测量只建立了两个基准点。但在条件允许的情况下，一般应建立3个～4个基准点，这样可以检验基准点是否稳定。自由设站点1、点2布置于基坑开挖影响范围之内的场地。由于自由设站点的坐标会随着基坑的开挖而发生轻微的变化，所以每次在进行测量之前都要对自由设站1和自由设站2进行校核。

3.2测量精度分析

由于篇幅的限制，这里选择单一的徕卡TPS1200全站仪进行精度分析。根据仪器的标称精度可知，其测角精度为±1.0 mm，测距精度为±(1.0 mm+1 ppm×S)，经过多次验证统计，在人工照准目标200 m距离内，其实际角度测量精度mβ1=mβ2=mβ3=mβ=±0.38″，测距精度mS=±0.4 mm[10,11]。根据实际测量情况，两个自由设站点的位置只会发生轻微的变动，为了便于分析，可以认为S1，S2在整个监测周期中保持不变，且有S1≈100 m，S2≈10 m，β1=20°,β2=0°，则mS1=mS2=±0.4 mm；为了提高精度，强制归心装置的观测墩和棱镜台采用强制对中装置，则有m仪器对中1=m仪器对中2=m仪器对中3=m仪器对中=0 mm，mi1=mi2=mi3=mi=±0.2 mm，m偏心1=m偏心2=m偏心3=m偏心=0 mm,mv1=mv2=mv3=mv=0 mm。代入式(5)可求得m1=±0.30 mm；同理代入式(6)可得m2=±0.4 mm。

结合式(7)，分析对不同斜距S和垂直角β以及在有强制归心装置的观测墩和棱镜台采用强制对中装置的情形下进行精度分析，如表1所示。

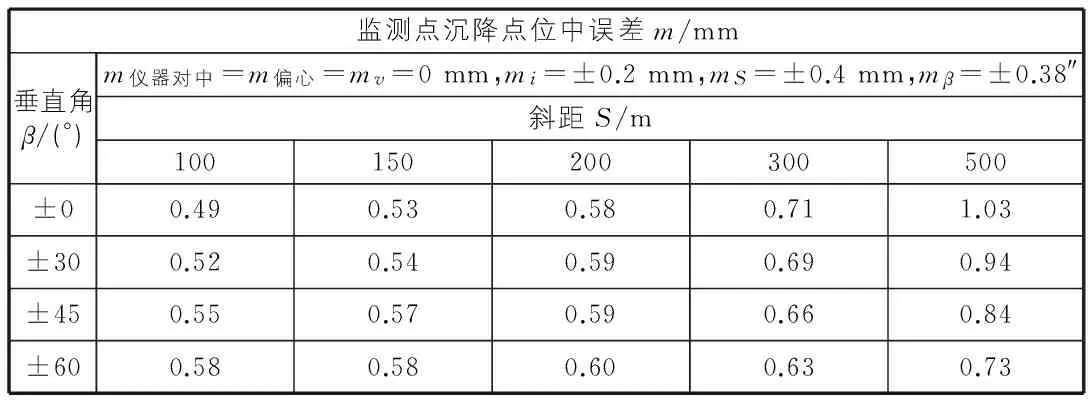
表1　在二重自由设站下监测点沉降精度分析

从表1中可以得出以下结论：

1)在斜距不大于300 m时,采用具有强制归心装置的观测墩和具有强制对中装置的棱镜台时，可以满足基坑沉降三等精度的要求[10]；从表1中数据上看，在斜距不大于500 m时，也基本满足三等精度的要求，但此数据是在200 m内mS=±0.4 mm，mβ=±0.38″的经验数据上求得，所以在斜距为500 m时的精度被提高，不能满足三等精度的要求。

2)在斜距不大于300 m时，沉降的精度随着垂直角的增大而减小，大于300 m时，沉降的精度随着垂直角的增大而增大。

3)以上精度分析数据表面，尽量选用低重自由设站，这样可以提高测量精度。

4　结语

1)在基坑开挖形状和周围环境较为特殊，一个或多个独立自由设站也无法对整个监测网实施监测时，可以考虑采用多重自由设站的方法来建立监测网，以对整个基坑进行实时监测。

2)全站仪基于多重自由设站的基坑沉降监测的方法，能有效解决基坑在特殊的地形和地物条件下，对于稳定基准点与监测点之间不能通视的问题。该方法测站摆放灵活，网形多变，能快捷的对整个监测网进行监测。

3)该工程最大斜距约为150 m，沉降监测按三等精度要求执行。沉降通过对二重自由设站水平位移监测精度的分析，采用徕卡TPS1200全站仪，具有强制归心装置的观测墩和具有强制对中装置的棱镜台，可以满足沉降监测三等精度的要求。

4)为了能够满足精度的要求，多重自由设站的个数不宜较多，所以一般采用该方法确定1个～2个自由设站点较为合适。

[1]杨雪峰,刘成龙,罗雁文.基于自由测站的基坑水平位移监测方法探讨[J].测绘科学,2011,36(5):153-154.

[2]骆旭佳,高飞,胡小华,等.全站仪自由设站在测绘中的应用[J].勘察科学技术,2010(1):44-45.

[3]王刚.全站仪结构原理与发展分析[J].现代建设,2013,12(10):34-36.

[4]刘沛.自动化全站仪在高层建筑基坑变形监测中的应用[J].测绘与空间地理信息,2011,34(3):239-141.

[5]武汉测绘科技大学测量平差教研室.测量平差基础[M].北京：测绘出版社，1996.

[6]孔祥元,梅是义.控制测量[M].武汉:武汉大学出版社,2002:270-279.

[7]冯显堂.大气折光系数的取值[J].鞍钢技术,1996(2):48-50.

[8]汪孔政.全站仪监测基坑水平位移精度分析[J].建筑技术,2009,40(2):153-154.

[9]晏红波,黄腾,邓标.智能全站仪精密三角高程测量替代二等水准测量[J].水电自动化与大坝监测,2007,31(4):43-46.

[10]GB 50026—2007,工程测量规范[S].

[11]王登杰,田文宝.基于差分技术的基坑位移监测方法研究[J].工程勘察,2015(2):79-84.

Research on the method of multiple free station based settlement monitoring of foundation pit

Luo BochengWu Haike

(CivilEngineeringCollege,GuizhouUniversity,Guiyang550025,China)

Introduced the principle of trigonometric leveling with total station instrument, and taking the Guling’an engineering of Maotai No.4 bridge as an example, analyzed the total station measuration displacement and settlement precision and the corresponding measuring instruments are selected to achieve the purpose of real-time, fast and accurate response of foundation pit.

complex foundation pit, multiple free station, settlement monitoring, monitoring point

1009-6825(2016)23-0066-03

2016-06-07

罗伯成(1989- )，男，在读硕士；吴海科(1990- )，男，在读硕士

TU433

A