海底管道砂沉积模拟研究
张文欣, 周晓红, 陈宏举
(中海油研究总院, 北京 100028)
海底管道砂沉积模拟研究
张文欣, 周晓红, 陈宏举
(中海油研究总院, 北京 100028)
海底混输管道运行一段时间后,管道内部砂沉积等会导致管道通过量减小,明显降低缓蚀剂效率,加速管道底部磨蚀,甚至造成清管器卡堵事故。以位于海上某油田群A平台至B平台的海底混输管道为基础,根据现场实际数据合理建模,采用FLUENT软件进行数值模拟,研究了海底管道水平段以及弯管段在砂含量、砂粒径、砂密度以及流速等参数不同时的砂沉积规律。模拟结果表明,海管沿程沉砂量与含砂量、砂粒径、砂密度正相关,与流速负相关;而沉砂量最大位置规律相反。平均沉砂量对各参数的敏感性从高到低依次为含砂量、流速、砂粒径、砂密度。
砂沉积;FLUENT模拟;弯管段;变量分析;沉积规律
某海上油田群A平台至B平台海底管道的设计年限为15年,但投入使用不到5年就出现许多漏点,严重影响了油田的正常生产。泄漏点如图1所示,新老漏点共出现40余次,内管漏点基本都出现在海管中后部及出口段,在管道底部有砂沉积的位置腐蚀最严重。砂沉积厚度仅为几毫米,对管道流通面积影响很小(不足1%),但砂覆盖管道内表面,阻挡了缓蚀剂覆盖金属表面,使得缓蚀剂在金属表面的实际浓度小于注入浓度,影响了缓蚀剂的效率(仅为20%)[1]。

图1 泄漏点示意图
因此,研究海管中砂沉积规律对于缓蚀剂效率和清管具有指导意义。目前对于管道输送砂沉积的研究主要针对于浆体输送,即砂含量较大(大于10%)的水平管道输送[2-4],而对于砂含量较低(小于1%)的流体输送以及海底管道弯管部分的研究甚少。因此,本文通过FLUENT数值模拟海底管道低砂含量下水平管段和弯管道的砂沉积规律,论证数值模拟的可行性,以此预测砂沉积的时间和位置,指导确定清管周期,降低砂沉积导致的腐蚀风险。
1 海管砂沉积模型建立
1.1模型建立
含砂管流为典型的低相含率液-固两相流,综合考虑模型适应性与计算效率,针对本研究采用多相流混合(Mixture)模型[5-6]和标准k-ε湍流模型[7]进行模拟。
检测报告指出管道底部有砂沉积,且内管穿孔多位于6点钟位置。为提高计算效率,选取管道中心纵向对称剖面的二维模型来建模。砂含量低,沉积的砂只会在管道底部形成极薄的一层砂层,因此对管道底部边界层网格局部加密。管道长径比极大,因此采用等比例过渡法(见图2),生成网格扭曲度极低(小于0.05),网格质量极高;可实现网格无关性的二维网格数不超过10万,大大减少了网格数量,提高了模拟效率。

图2 模型网格
通过全管段建模模型进行模拟,得到水平方向上壁面沿程沉砂量。如图3所示,中间水平管段沉砂量几乎不变,而入口弯管段和出口弯管段显著变化,因此通过分段法(见图4)着重研究。
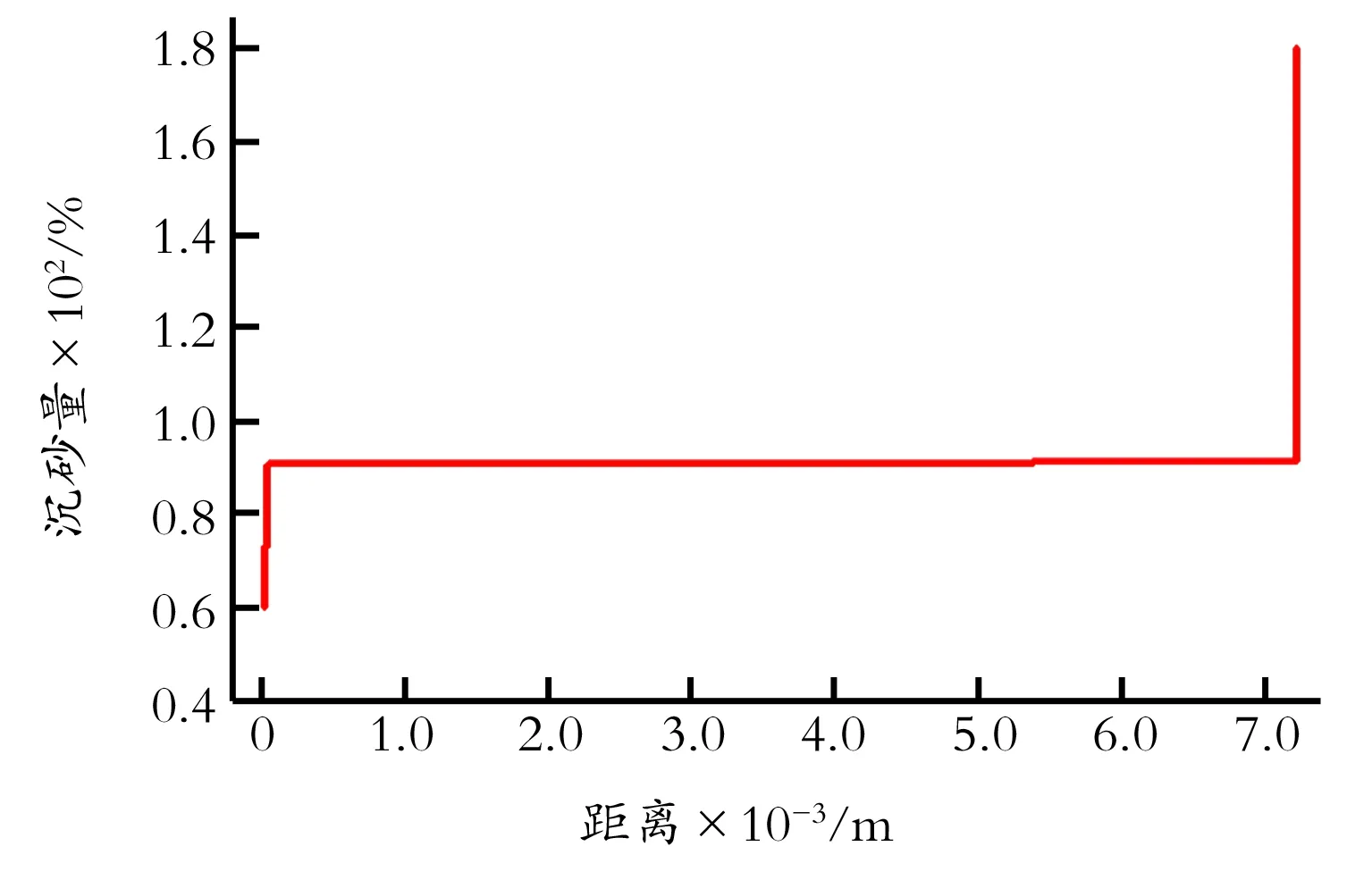
图3 7 200 m全管段沿程沉砂量
入口弯管水平段选取弯管连接10 m立管和100 m水平管,水平段为100 m无起伏管道,出口弯管水平段为弯管连接50 m水平管和10 m立管(立管高度对于本研究的影响可以忽略)。

图4 A平台至B平台海管分段示意图
1.2理论基础
海底混输管道流体中含有少量砂,可将其视为浆体,利用浆体的相关运动理论对砂的沉积规律进行预测[11]。当清水与固体颗粒构成的沉降性浆体在水平管道内流动时,由于受固体颗粒浓度分布的影响,其速度分布断面与清水等的速度分布断面相比,会发生不对称性变化[3],即非均质流在管道中心上方的速度较清水大,而在下方的速度较清水小[8]。这种现象将随着固体颗粒浓度的增加,变得越来越明显[3]。
通过实验观察,砂在管道中的输送方式随着流速增大可以分为三种,即静止砂层、运动推移砂层(流速超过临界流速)和悬移砂层。判断管道底层固体颗粒是否静止不动,需要进行受力分析,如图5所示。

图5 管道底层固体颗粒受力分析
当式(1)成立时[10],管道底层颗粒静止不动。
(1)
式中:水流拖曳力FD[10]、摩擦力[10]、耗散力Fi[10-11]的计算公式分别如表1所示。
1.3计算条件设定
根据海管温度压力流量现场数据,海管输送介质的含水率在60%左右,由于密度原因,水在海管底部流动。因此,针对水进行携砂分析,即可预测海管的砂沉积规律[9]。
海底管道模型入口边界条件设置为Velocity-inlet(速度入口),出口边界条件设置为outflow(自由流出口),通过FLUENT的profile文件保证数据的连续性,采用瞬态模拟以精确描述流体动态过程。Y方向重力加速度设为-9.8 m/s2。根据实际工况,给定各参数数值,通过单一变量法进行研究。
基础计算条件为管径D=0.273 m,含砂量1×10-5,流速v=0.53 m/s,砂粒径d=50 μm,砂密度ρ=2 650 kg/m3。

表1 管道底层固体颗粒受力计算公式
2 海管入口弯管与水平段砂沉积规律分析
2.1含砂量对砂沉积的影响
基础计算条件不变,选取含砂量1×10-7、1×10-6、1×10-5、1×10-4分别进行模拟,结果如图6所示。由图6可以看出,当运行稳定后,沿水平管段方向,沉砂量逐渐增加至稳定沉砂量。随着海管入口含砂量的增加,相同位置处的沉砂量显著增加。当含砂量增加时,FD、Fi和Ff相同,而且颗粒间存在干涉阻力,含砂量越大,单一颗粒受到周围颗粒的阻力越大。含砂量越大,在沉砂概率相同的情况下,沉砂量必然增加。
如图6所示,随着含砂量增大,最大沉砂位置坐标(即弯管连接水平段从砂开始沉积到达到最大稳定沉砂量时的位置)逐渐减小,分别为158、115、100、90 m。同一砂粒受其他砂粒阻力越大,该砂粒在前段沉积越快,即最大沉砂位置坐标与含沙量成负相关。

图6 含砂量不同时的沉砂量
2.2砂粒径对砂沉积的影响
基础计算条件不变,选取砂粒径为10、50、100、200 μm分别进行模拟,结果如图7所示。由图7可以看出,随着砂粒径增大,Ff增大幅度大于FD与Fi之和的增大幅度,且颗粒间阻力更大,因此同一位置沉砂量增加。当砂粒径为100 μm和200 μm时,沿程沉砂量均先增大再减小而后趋于稳定,粒径较大导致受力的影响因素变化较为复杂。当粒径大于等于50 μm时,沉砂量在100 m附近基本稳定,且数值相近;而粒径为10 μm时沉砂量持续增加且远未达到稳定沉砂量,而且明显小于50 μm以上粒径的沉砂量,由此可以看出存在临界粒径使得沉砂量可以明显减小沿程沉砂量。随着砂粒径增大,沉砂量最大位置坐标并非单调递减。因此,砂粒径对沉砂量的影响较为复杂,需要深入研究。

图7 砂粒径不同时的沉砂量
2.3砂密度对砂沉积的影响
基础计算条件不变,选取砂密度为2 500、2 650、2 800、3 000 kg/m3分别进行模拟,结果如图8所示。

图8 砂密度不同时的沉砂量
由图8可以看出,沿水平管段方向,沉砂量逐渐增加至稳定沉砂量。随着砂密度的增加,相同位置处的沉砂量相应增大,且稳定沉砂量虽略有差值(0.549 4%、0.552 7%、0.553 7%、0.554 2%),但基本一致。固体颗粒密度越大,固体颗粒也就越重,摩擦力Ff会显著增大,大于FD增大幅度,而Fi不变[3]。砂密度越大越容易沉降,所以最大沉砂位置坐标相应减小,即成负相关。
2.4流速对砂沉积的影响
基础计算条件不变,选取流速为0.53、1.00、1.50、2.00 m/s分别进行模拟,结果如图9所示。由图9可以看出,随着流速增加,沿程沉砂量逐渐增加至平稳。当流速增加时,对于单一砂粒的水流拖曳力FD显著增大,呈指数增长,而Fi和Ff不变,即同一砂粒越难达到受力稳定而沉积。这说明流速越大,流体携砂能力越强,砂在管道中沉积的可能性越小。因此,随着流速增加,沉砂量逐渐减小。同一位置的砂粒在水平方向受力更大,则沉砂位置后移,即沉砂量最大位置坐标与流速成正相关。

图9 流速不同时的沉砂量
2.5弯管处砂沉积规律分析
为了更好的研究弯管处的砂沉积规律,取弯管段沉砂量,以弯管角度为横坐标得到不同参数下的弯管处沉砂量,结果如图10-12所示。




图10 入口弯管处的沉砂量
图10中(a)、(b)、(c)、(d)的研究条件与2.1至2.4中的研究条件分别对应。当含砂量、砂粒径、砂密度以及流速增大时,弯管处的沉砂量均先增大后减小,但是其沉砂量远小于水平段沉砂量,仅相当于后者的1%。


图11 沿程沉砂量云图
沿程沉砂量云图如图11所示,在距入口弯管100 m的水平段明显有薄沉砂层,而弯管处基本无法观察到沉砂量。因为液体从立管处向下流动遇到弯管产生速度变向,虽造成弯管壁面处流速减小(见图12(a)),但湍流强度急剧增加(见图12(b)),导致砂粒难于沉积;弯管内侧的砂流速极大,且壁面处湍流强度较大,易造成磨蚀,应引起重视。
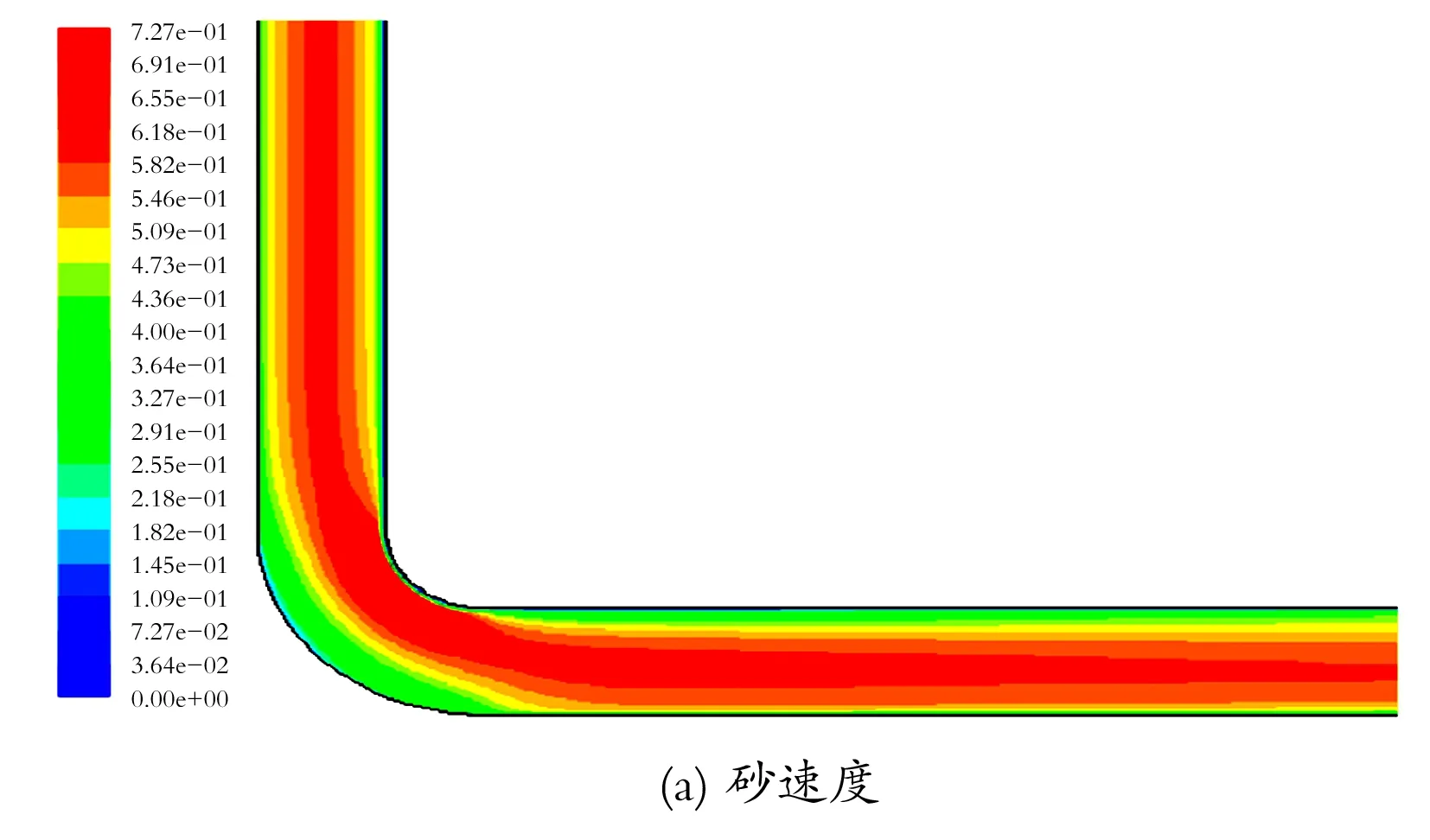
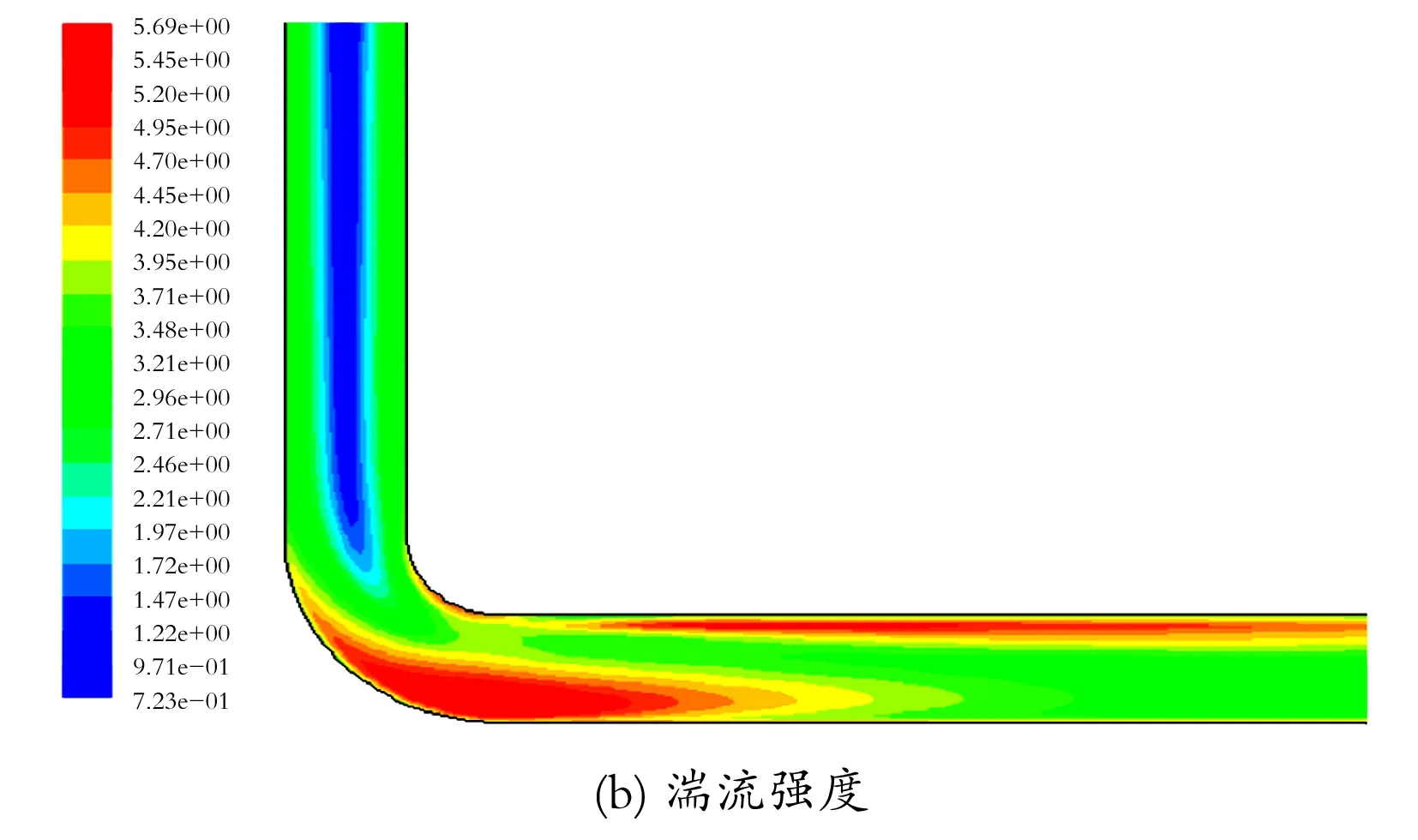
图12 弯管沿程砂速度和湍流强度云图
2.6参数敏感性分析
将各参数不同时的平均沉砂量进行(分段)线性拟合,参考斜率进行参数敏感性分析。平均沉砂量随含砂量、砂粒径、砂密度和流速的线性拟合曲线分别见式(2)至(5):
(2)
(3)
(4)
(5)
式(2)至(5)中y为平均沉砂量,x分别为含沙量、砂粒径、砂密度和流速。
通过各拟合曲线的斜率,可以更直观的看出平均沉砂量对各参数的敏感性,即两者成正相关。对比式(2)至(5),各参数对平均沉砂量的影响由大到小分别为含沙量、流速、砂粒径,而砂密度影响很小。
3 出口弯管段砂沉积规律分析
与入口弯管处沉砂量极小不同,出口弯管前水平段的沉砂量基本稳定(见图13(a)),而弯管处的沉砂量(见图13(b))明显增大。如图14所示,弯管处砂流速明显降低,而湍流强度到达弯管上部直至立管段急剧增大,极易造成磨蚀。

图13 沿程沉砂量云图
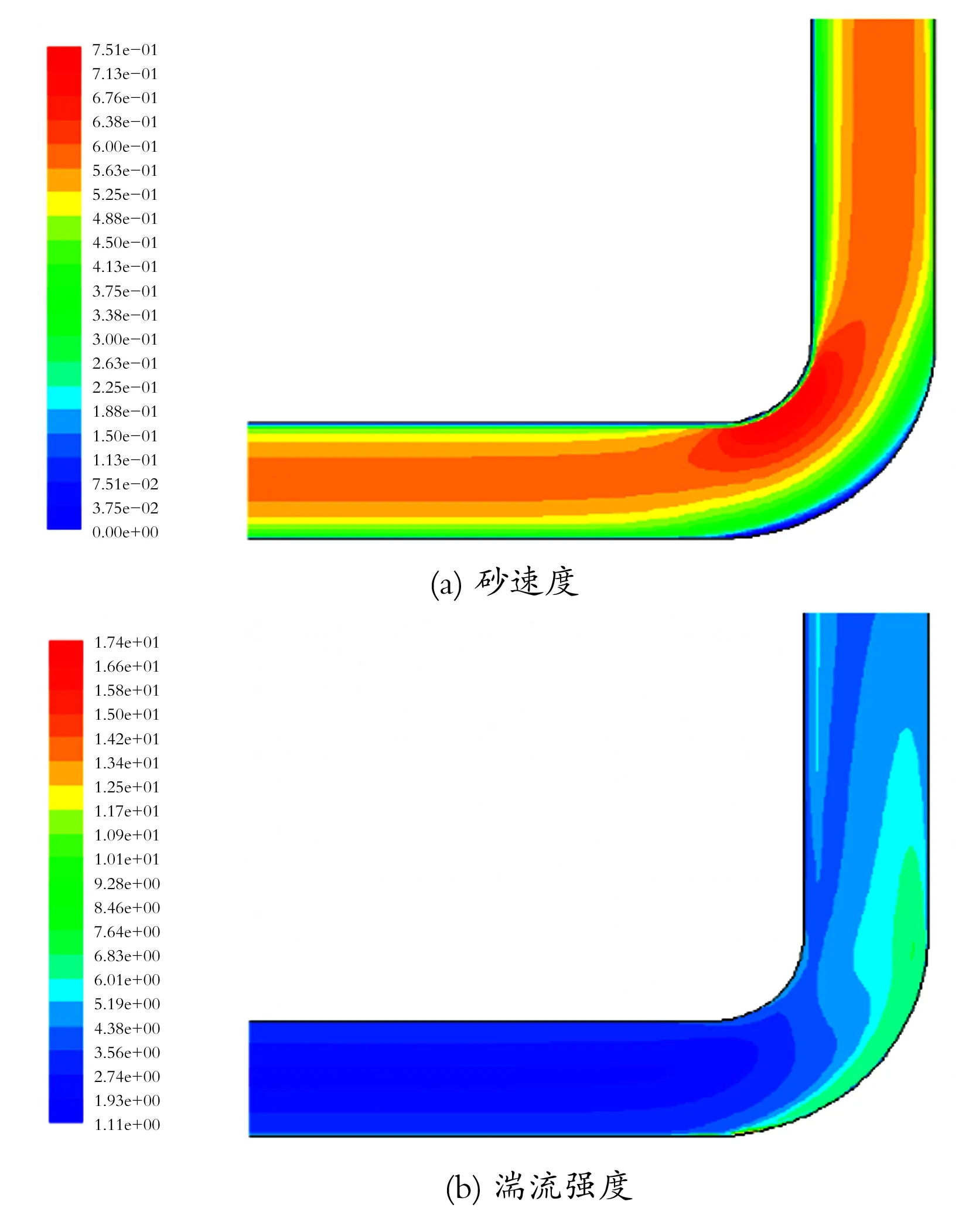
图14 弯管沿程砂速度和湍流强度云图
3.1含砂量不同时的砂沉积规律分析
如图15所示,在弯管前的水平管段,沉砂量基本保持稳定,而到达弯管处时沉砂量急剧增大到最大值(稳定沉砂量的2.0~2.5倍)又逐渐减小。但含砂量为1×10-4时,弯管处最大沉砂量急剧增加到稳定沉砂量的10倍。含砂量越大,在弯管处受到的阻碍越大,在相同沉积概率下,向立管流动时纵向的沉降量越大,因此弯管底部沉砂量越大。而随着弯管向立管的过渡,因湍流强度逐渐增大,弯管壁面砂沉积迅速减少。
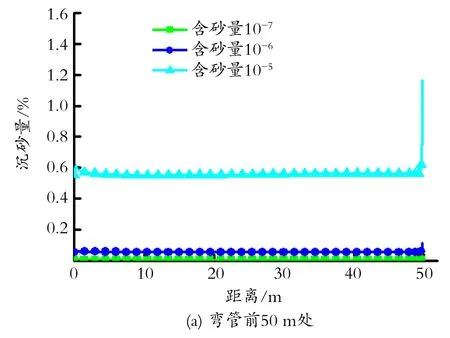



图15 含砂量不同时的沉砂量
3.2砂粒径不同时的砂沉积规律分析
如图16所示,在弯管前的水平管段,沉砂量基本保持稳定,而到达弯管处时沉砂量迅速增大至最大值(稳定值的2.0~2.5倍)又逐渐减小至稳定值。砂粒径越大,相同密度下的单一颗粒重力越大,越容易沉积,则沉积量越大。与2.2中规律相似,当粒径大于等于50 μm时,沉砂量在相近位置达到了相近值,而粒径为10 μm时沉砂量明显小于较大粒径时。因此可以说明存在临界粒径以减小砂沉积的影响。


图16 砂粒径不同时的沉砂量
3.3砂密度不同时的砂沉积规律分析
如图17所示,在弯管前的水平管段,沉砂量基本保持稳定,而到达弯管处时沉砂量迅速增大至最大值(稳定值的2.0~2.5倍)又逐渐减小。砂粒径相同时,密度越大则重力越大,越容易沉积,导致沉积量越大。如2.6所述,砂密度对沉砂量的影响最小,这也体现在了弯管处沉砂量上。
3.4流速不同时的砂沉积规律分析
如图18所示,在弯管前的水平管段,沉砂量基本保持稳定,而到达弯管处时沉砂量迅速增大至最大值(稳定值的2.0~2.5倍)又逐渐减小。随着流速增加,单一颗粒受到的升力大于弯管的阻碍作用,且湍流强度增大,使得砂粒更均匀的分布在液体中而难于沉积于壁面,因此沉砂量减小。


图17 砂密度不同时的沉砂量
4 结论
本文以海上某油田的海底混输管道为基础,根据现场数据合理建模,并设定含砂量、砂粒径、砂密度和流速等参数范围,通过FLUENT软件进行数值模拟,分析海底管道的砂沉积规律,得出以下结论:
(1) 海管水平段的沉砂量逐渐增大并最终达到稳定值,而在出口弯管段达到极大值,数值模拟结果与实际泄漏点位置相对应。
(2) 海管沿程沉砂量与含砂量、砂粒径、砂密度正相关,与流速负相关;而沉砂量最大位置规律相反,这说明数值模拟结果与实际管流情况一致。
(3) 平均沉砂量对各参数的敏感性从高到低依次为含砂量、流速、砂粒径、砂密度。
(4) 利用弯管角度对其沉砂量进行分析具有普遍适用性,入口弯管段沉砂量非常小,而出口弯管段沉砂量在一定时间内急剧增加应引起重视。


图18 流速不同时的沉砂量
[1]贾旭,常玮,黄俊,等. 南海某海底管道腐蚀原因分析[J]. 全面腐蚀控制,2013(8):33-37.
Jia Xu, Chang Wei, Huang Jun, et al. Corrosion reason analysis of one subsea pipeline in south china sea [J]. Total Corrosion Control, 2013(8):33-37.
[2]张兴荣. 管道水力输送[M]. 北京:中国水利水电出版社,1997:42-44.
[3]张士林. 沉降性浆体速度与浓度分布耦合模型及迁移速度研究[D].大连:大连理工大学,2005:53-54,93-98.
[4]费祥俊. 浆体与粒状物料输送水力学[M]. 北京:清华大学出版社,1994:252-254.
[5]于勇. FLUENT入门与进阶教程[M]. 北京:北京理工大学出版社,2008:174.
[6]韩占忠,王敬,兰小平. FLUENT-流体工程仿真计算实例与应用[M]. 北京:北京理工大学出版社,2010:19.
[7]于爽,阿斯汉,孙策,等. T型集输管路油水两相流数值模拟[J]. 石油化工高等学校学报,2015,28(4): 94-98.
Yu Shuang, A Sihan, Sun Ce,et al. Numerical simulation on oil-water two-phase flow in T-tube of gathering pipeline [J]. Journal of Petrochemical Universities, 2015, 28(4):94-98.
[8]许振良. 非均质流速度分布与水力分布的研究[D].沈阳:东北大学,1999:15-20.
[9]蒋文明,曹学文,王国栋,等. 南堡油田海底管道砂沉积预测与模型检验[J]. 油气储运,2012,31(8):591-593.
Jiang Wenming, Cao Xuewen, Wang Guodong, et al. Sand deposit prediction and model checking of submarine pipeline in Nanpu oilfield [J]. Oil and Gas Storage and Transportation, 2012, 31(8): 591-593.
[10]甘正旺. 沉降性浆体水平管道堆积速度的研究[D].阜新:辽宁工程技术大学,2004:49-54.
[11]Misaki Sato Hiroshi, Otsuka Yiyu, Noda Yoshiroku, et al. Irregular particle swarm interference terminal velocity [J]. Nippon Mining Journal, 1988, 104(1206): 505-512.
(编辑王亚新)
Numerical Simulation of Sand Depositional Rule in Subsea Multiphase Pipeline
Zhang Wenxin, Zhou Xiaohong, Chen Hongju
(ResearchInstituteofChinaNationalOffshoreOilCorporation,Beijing100028,China)
Sand deposit will be formedinside of subsea multiphase pipeline after operating for a period of time, which will lead to diminution of passable area, reduction of inhibitor efficiency, acceleration of corrosion, and even cause the PIG block accidents. In this article, the geometrical model and physical model with field dataare set up building upon the subsea multiphase pipeline from platform A to B in a group of offshore oil and gas fields.Numerical simulations by FLUENT are performed in order to study the sand depositional rule of straight section and bend section according to the variation of parameters such as sand content, particle size, density and flow rate. The research shows that sand depositional amount is positive correlative with and content, particle size, density and negative with flow rate, and the rule of sand depositional maximum position is opposite. The sensitivity of parameters to average sand depositional amount is sand content, flow rate, particle size and density from high to low.
Depositional sands; FLUENT numerical simulation; Bbend section; Variables analysis; Depositional law
1006-396X(2016)01-0086-07
投稿网址:http://journal.lnpu.edu.cn
2015-03-19
2015-04-13
张文欣(1987-),女,硕士,工程师,从事海管工艺的设计和研究工作;E-mail:zhangwx20@cnooc.com.cn。
TE345
Adoi:10.3969/j.issn.1006-396X.2016.01.017

