基于改进模拟退火算法的横波速度求取

王璞，吴国忱，李伟

（中国石油大学（华东）地球科学与技术学院，山东 青岛 266580）

基于改进模拟退火算法的横波速度求取

王璞，吴国忱，李伟

（中国石油大学（华东）地球科学与技术学院，山东 青岛 266580）

模拟退火算法能够较好地实现全局最优化求解。基于非均匀变异思想，文中给出了一个新的模拟退火算法扰动模型，该模型具有一定的灵活性，通过选取合适的扰动模型参数，可以达到减少迭代次数、提高收敛速度的目的。在模拟退火算法退温前，增加最优解附近小范围内寻优，以减少对扰动模型的依赖，通过改进，模拟退火算法得到了优化。数值实例分析表明，改进后的模拟退火算法比常规模拟退火算法在迭代次数和扰动次数上有一定的优势。采用该算法，利用DEM模型进行横波速度求取后，与测井横波比较，误差较小，从而验证了新模拟退火算法的实用性和有效性。

模拟退火；最优解；迭代次数；横波

0　引言

模拟退火算法作为一种随机性全局最优求解方法，具有广泛的适用性，很多学者对其进行过研究［1］。模拟退火算法最早是由N.Metropolis等［2］于1953年提出的，常规的模拟退火算法是指Kirkpatrick等［3］提出的Metropolis算法。非线性反演算法往往受到计算效率的制约，为了提高模拟退火的计算效率，Ingber［4］提出的非常快速模拟退火算法（VFSA）中，扰动模型采用了依赖于温度的似Cauchy分布代替了常规模拟退火算法中的高斯分布；Press等［5］采用单纯形法与模拟退火算法相结合的算法；Penna［6］由广义Gibbs分布给出新的接受概率计算表达式；姚姚［7］从模拟退火最低温度的选择入手，根据模拟退火算法与统计力学的Gibbs-Markov模型之间的关系导出临界温度的近似表达式；纪晨等［8］在模拟退火算法中引入均匀设计方法；文浩［9］采用遗传模拟退火算法，对阿尔奇公式中的a，m，n参数进行估计，并通过现场应用对测井数据进行了模拟计算；闫安菊等［10］借鉴模拟退火的冷却思想，设定高斯滤波尺度因子和梯度阀值为时间的函数，构建了各向异性扩散滤波模型。模拟退火算法是建立在随机搜索方法基础之上的，因此，扰动模型需要满足在解分布的最大范围内均匀随机找值，达到对目标函数的精度要求。

本文以横波速度预测为例进行分析，来解决实际工区中横波信息缺失的现象。在求取横波速度时，需要用到储层孔隙度，然而实际资料中泥岩层段孔隙度是不作解释的。这就需要基于非线性全局寻优算法来重构孔隙度，在反演孔隙度时，模拟退火算法是应用较多的一种方法。本文基于DEM模型［11］，在纵波速度约束下，用改进的模拟退火算法对某工区1口砂泥岩井进行应用分析，取得了很好的效果。

1　模拟退火算法基本原理

模拟退火算法的思想源于物理中固体物质的退火过程与一般组合优化问题之间的相似性，它把优化问题的可行解看成是材料的各种状态，将优化目标视为材料的能量或者熵。在优化过程中，它不仅接受让目标函数变好的解，对于让目标函数变差的解也会以某一概率接受，这样可使算法跳出局部最优解，最终获得全局最优解。

模拟退火算法的一般步骤：1）给定初始温度T= T0，在解可能取到的范围内随机产生初始状态X=X0，并求取目标函数值F（X0）。2）基于上一个状态扰动产生一个新解X1，求取目标函数F（X1），进而得到ΔF=F（X0）-F（X1）。3）若ΔF＜0，则接受新解X1；若ΔF＞0，则新解以概率P=exp（-ΔF/T）进行接受。4）在同一温度T0下，重复步骤2）和3），即对解进行一定次数的扰动。5）将温度T缓慢退温。6）重复步骤2）至5），直至满足某个收敛准则为止。

2　模拟退火算法的改进

在Ingber［4］给出的非常快速模拟退火方法中，在模型扰动时，采用依赖于温度的似Cauchy分布来产生新的扰动解，在高温时对应大范围搜索，低温时对应当前解附近小范围搜索，有助于加快收敛速度。扰动模型的表示形式为

式中：X（i）为扰动产生的第i个解；Xmax和Xmin分别为X可取的最大值和最小值；ε为［0，1］范围内均匀分布的随机数。

在生成新扰动解的过程中，可将非均匀变异思想与温度结合创建新的扰动模型。非均匀变异算子要求在算法初始阶段能够均匀地搜索整个解空间，在算法后期则集中于若干小范围内精确搜索。搜索中给出的扰动模型可表示为

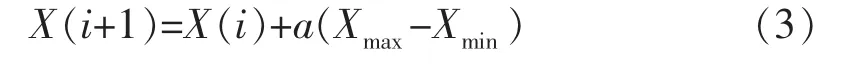
式中：T（i）为第i次退温的温度；Tmax为温度可取最大值；b是控制搜索范围在退温时减小快慢的量。

由式（4）可知，a既保证了最大范围内寻优，又保证了扰动模型在温度高时对应大范围搜索、在温度低时对应小范围搜索的特性。相比似Cauchy分布产生的扰动解，该方法具有较好的灵活性。通过调节控制变量b，可以有效提高模拟退火寻优速度。b值的选择不能太大也不能太小：b值太大，迭代次数会减少，容易陷入局部最小值；b值太小，寻优时间会增长。

以上2种产生扰动新解的方法，有个共同的特点，即在高温时对应大范围搜索，在低温时对应当前解附近小范围搜索。常规模拟退火寻优过程（见图1a，1b）为：在某一温度时，模拟退火寻优过程如图1a所示，寻优半径为R1，X*为准确解位置，通过寻优，最优解由X1变为X2；寻优范围R1依赖于温度T，即温度T不变时，寻优范围固定。退温时，寻优过程如图1b所示，搜索范围由R1变为R2，然后循环执行图1a和图1b所示流程，直至找到全局最优解。其中，由1a到1b为常规模拟退火流程，由1a到1c，再到1d为改进后的流程。

对于图1a所示温度不变的过程，经过改进，分为2步完成。第1步先找到最优解X2；第2步，设定一个较小的搜索范围R3，即a取0.01等较小值（见图1c）。为了不影响寻优速度，在搜索范围R3内只需进行较少次数的搜索。由于该搜索范围很小，因此，如果R3范围内有更好的解X3，是极易找到的，反之，保持解X2不变。退温时，为了防止出现局部最优解，搜索范围仍采取依赖于温度T的R2，最优解X3作为下次循环的初值（见图1d）。通过改进，扰动产生新解的次数减少，同时也减少了对初值和扰动模型的依赖。

和常规模拟退火算法比较，改进后的模拟退火算法扰动模型基于非均匀变异思想，大大加快了收敛速度，同时在退温前增加最优解附近小范围内寻优可以减小对扰动模型的依赖，从而减少了扰动模型的随机赋值。

3　数值模型分析

为了验证该算法改进后的寻优效果，构建了纵波约束下反演孔隙纵横比的岩石物理模型，采用DEM模型。基质矿物为纯砂岩，流体为油水混合，具体参数如表1所示。

表1　模型参数

为了方便说明，将上述分析的模拟退火算法进行了分类表示。方法1的扰动模型为依赖于温度的似Cauchy分布；方法2的扰动模型基于非均匀变异思想；方法3为改进的方法1，即方法1中退温前采取两步法；方法4指改进的方法2，即方法2中退温前采取两步法。

图2比较了初始孔隙纵横比为0.4时方法1和方法2的收敛速度。可以看出，方法2通过调节参数b，可以提高收敛速度。根据式（4），随着b值的增大，在退温过程中，寻优范围减小的速度加快，理论上减小了大范围搜索全局最优解的次数，因此，参数b不宜取值太大，以免出现局部最优解。通过数值分析，可以看出b值取6左右，既可以有效地减少迭代次数，又可以避免迭代次数过少而产生局部最小值。精确b值的确定，还有待进一步研究。由图2还可以看出，方法2虽然减少了迭代次数，但是其预测精度并没有受到干扰，能较好地求出孔隙纵横比。

图2　孔隙纵横比随迭代次数变化

由图3可以看出，初始孔隙纵横比取0.4，b取5时，4种方法都能较准确地找到精确解。在找到全局最优解之前，方法3和方法4比方法1和方法2对解的扰动次数要少，即温度不变时，通过增加最优解附近小范围内寻优，减少了对扰动模型的依赖。但是，由于增加了区域R3的寻优，收敛速度没有得到改善。

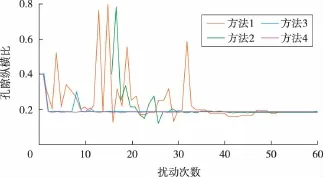
图3　孔隙纵横比随扰动次数变化

4　井资料实例应用

实际工区储层解释时，往往缺失横波信息，因此采用模拟退火方法2和方法4，对某地区1口井进行了横波求取试算。为验证方法的有效性，所取井段为有横波信息的砂泥岩层，采用DEM模型，用Gassmann方程进行流体替换，模型中模拟退火算法用来重构孔隙度，即计算虚拟孔隙度，来解决实际生产中孔隙度解释不准确，或者泥岩段没有孔隙度信息的情况。根据上述数值分析，2种模拟退火方法都能较准确地找到全局最优解。这里运用2种模拟退火方法，在纵波速度的约束下，由DEM模型求取横波速度（见图4）。

图4　横波速度预测结果

由图4a可以看出，通过调节孔隙度，计算纵波速度和实测纵波速度，误差非常小。扰动模型都基于非均匀变异思想，不同的是图4c考虑了退温前小范围内寻优。可以看出，2种方法求取的横波速度与实际测井横波速度都吻合较好，误差较小。图4b证明了基于非均匀变异思想的模拟退火算法在实际应用中的适用性，图4c证明了同时考虑非均匀变异思想带来的模型扰动和增加退温前小范围寻优得到的模拟退火算法也具有很好的适用性，即验证了改进后模拟退火算法的有效性。

5　结束语

本文对常规模拟退火算法依赖于温度的似Cauchy分布扰动模型进行了改进，改进后的扰动模型基于非均匀变异思想，大大提高了收敛速度。另外，模拟退火退温前，增加最优解附近小范围寻优，可以减小对扰动模型的依赖，从而减少了扰动模型的随机赋值。对改进后的模拟退火算法进行了数值实例分析和测井资料实例应用，结果表明，改进后模拟退火算法和常规模拟退火算法相比，在迭代次数和扰动次数上具有优势。通过测井实例应用，验证了该方法的实用性和有效性。

［1］张霖斌，姚振兴.快速模拟退火算法及应用［J］.石油地球物理勘探，1997，32（5）：654-660.

［2］Metropolis N，Rosenbluth A W，Rosenbluth M N，et al.Equation of state calculations by fast computing machines［J］.The journal of chemical physics，1953，21（6）：1087-1092.

［3］Kirkpatrick S.Optimization by simulated annealing：Quantitative studies［J］.Journal of statistical physics，1984，34（5/6）：975-986.

［4］Ingber L.Very fast simulated re-annealing［J］.Mathematical and computer modelling，1989，12（8）：967-973.

［5］Press W H，Teukolsky S A.Simulated annealing optimization over continuous spaces［J］.Computers in Physics，1991，5（4）：426-429.

［6］Penna T J P.Traveling salesman problem and Tsallis statistics［J］. Physical Review E，1995，51（1）：R1-R3.

［7］姚姚.地球物理非线性反演模拟退火法的改进［J］.地球物理学报，1995，38（5）：643-650.

［8］纪晨，姚振兴.用于地震物理反演的均匀设计优化算法［J］.地球物理学报，1996，39（2）：233-242.

［9］文浩.遗传模拟退火算法在阿尔奇公式参数估计中的应用［J］.断块油气田，2008，15（1）：105-107.

［10］闫安菊，蔡涵鹏.改进的各向异性扩散滤波方法压制地震数据噪声［J］.断块油气田，2012，19（5）：592-595.

［11］Berryman J G.Single-scattering approximations for coefficients in Biot′s equations of poroelasticity［J］.The Journal of the Acoustical Society of America，1992，91（2）：551-571.

（编辑石爱萍）

Shear-wave velocity prediction based on revised and simulated annealing algorithm

Wang Pu，Wu Guochen，Li Wei
（College of Geosciences and Technology，China University of Petroleum，Qingdao 266580，China）

Simulated annealing algorithm is a good way to get the optimal solution.Based on the idea of non-uniform mutation，a new simulated annealing perturbation model is given in this paper.The perturbation model has a certain flexibility in its application.By choosing an appropriate parameter，the iterative number is reduced and the convergence speed is improved.In addition，before the temperature is decreased in the simulated annealing algorithm，the dependence on perturbation model can be reduced by adding a small search scope near the optimal solution.The results show that the revised method is better than traditional method from iterative and perturbing number.A rock physics model is constructed with DEM model to estimate shear-wave velocity under constraint of P-wave velocity.Compared with logging data，the computed shear-wave velocities have high accuracy.

simulated annealing；optimal solution；iterative number；shear-wave

国家重点基础研究发展计划（973计划）项目“多元多尺度地球物理信息映射关系及反演”（2013CB228604）；国家科技重大专项专题“复杂储层及流体识别方法与预测技术研究”（2011ZX05009-003-004）

TE319

A

10.6056/dkyqt201503013

2014-11-13；改回日期：2015-03-06。

王璞，男，1991年生，在读硕士研究生，研究方向为地震岩石物理。E-mail：826378939@qq.com。

引用格式：王璞，吴国忱，李伟.基于改进模拟退火算法的横波速度求取［J］.断块油气田，2015，22（3）：330-333. Wang Pu，Wu Guochen，Li Wei.Shear-wave velocity prediction based on revised and simulated annealing algorithm［J］.Fault-Block Oil&Gas Field，2015，22（3）：330-333.