基于改进趋近律的机械臂非奇异终端滑模控制
徐 杰, 柴发武
(1.黑龙江科技大学 电子与信息工程学院, 哈尔滨 150022; 2. 黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
基于改进趋近律的机械臂非奇异终端滑模控制
徐杰1,柴发武2
(1.黑龙江科技大学 电子与信息工程学院, 哈尔滨 150022; 2. 黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
针对终端滑模控制系统存在的收敛速度慢、抖振等问题,提出一种自适应趋近律。该趋近律可以根据状态变量距离平衡点的远近,自适应改变趋近速度,缩短趋近时间,同时减小抖振,可运用于机械臂非奇异终端滑模控制器的设计中。仿真验证结果表明:该算法能够较快地跟踪给定的期望轨迹,且抖振较小,有效提高机械手的性能。
自适应趋近律; 终端滑模控制; 机械臂
0 引 言
1948年,前苏联学者提出了滑模控制(Sliding mode control, SMC)。就控制系统本身而言,它是非线性的,连续性很差。该控制方法在工作中适时发生改变,总是使系统向设计的状态靠近,因此,SMC系统的鲁棒性增强。国内外学者开始进行SMC的大量探索,19世纪80年代末,SMC的研究取得了突破性的进展。美国学者Zak[1]提出了终端滑模控制(TSMC),指出如果将非线性的算法加入其中,系统能够在一定的时间里完成跟踪,但也会出现奇异现象。为了解决该问题,Feng等[2]提出了一种新的方法——非奇异终端滑模控制(NTSMC)。NTSMC及其各种改进算法[3-5],因为具有响应速度快,在一定的时间里能够收敛,跟踪的误差小等优点,受到很多研究者的推崇和应用。但NTSMC距离中心点远的区域时,跟踪速度变小,为此,研究者们设计了各种控制率,但都不可避免存在抖振问题。
针对抖振问题,许多国内外学者提出了不同的解决方案,主要分为两个方向:一是传统方向,梅红等[6]提出双幂次趋近律,姜君等[7]也对趋近律设计做了大量的探索。在文献[8-10]的研究中,学者们利用离散的方法,使系统的抖振得到了有效抑制,系统的鲁棒性提高。二是混合控制方向,国外一些学者提出了神经滑模控制[11-13],用来解决有界不确定项的轨迹跟踪问题。文献[14-15]将模糊控制和变结构相结合,采用模糊系统来逼近变结构框架中的每个细节和参数。
笔者在研究机械臂NTSMC的基础上,将NTSMC切换函数和改进趋近律同时应用到SMC设计中,在NTSMC消除奇异值的前提下,引入改进趋近律,根据系统状态距离平衡点的远近自适应调节趋近速度,缩短趋近时间,当接近滑模面时,又自适应地减小趋近速度及抖振,改善机械臂的跟踪精度,同时加强系统的鲁棒性。
1 机器人数学模型
基于拉格朗日方程描述N关节机械手系统的动力学方程为
(1)
式中:M(q)——非奇异的正定惯性力矩阵;

G(q)——重力项;
τd——不确定项或干扰,‖τd‖ τ——控制力矩; y——系统输出; q——N个关节位置向量,q=[q1,q2,…,qn]T。 机器人的控制目标:使系统输出q快速准确地追踪期望位置 qd。 假设qd二阶连续可导,定义状态变量 (2) (3) 由式(2)、(3)定义如下机器人位置跟踪误差状态方程: (4) 对于系统(4)采用幂次趋近律设计滑模控制器时,其趋近律为 (5) 当系统状态靠近滑模面时,趋近速度较小,能够削弱抖振,但系统状态较滑模面远时,由于趋近速度小,造成到达滑模面的时间较长,从而影响系统性能。另外,由于ε为固定值,不能自适应地改变趋近速度,其收敛特性不能达到最佳性能。文中提出自适应变速趋近律: (6) e=[e1,e2],k>0,ε>0,c>0,n>0,0<φ<1 。 可达性: (k+c‖e‖1)sTs<0。 (7) 式(7)满足可达性条件。 对于系统(4)定义非奇异终端滑模面 (8) (9) 取控制率τ=τ0+τ1+τ2+τ3,其中 (10) (11) (12) (13) 定理1对于式(4)所示的机器人系统,当选用式(8)所示的滑模面,采用反演控制率τ,则系统渐进稳定。 将τ=τ0+τ1+τ2+τ3代入,得 (k+c‖e‖1)s), (14) (k+c‖e‖1)s)≤0, 以二关节机械臂进行仿真实验, τd=0.1-0.2q+0.3-2q。 仿真主要分两步进行:首先,对系统进行NTSMC仿真,其次,对改进趋近律的NTSMC进行仿真,两种方法所取参数一致。 图1~3分别给出了NTSMC和改进趋近律的NTSMC的关节位置跟踪的仿真结果。从图1a、图2a和图1b、图2b可以看出,关节1的位置跟踪分别用了1.3和0.9s,关节2的位置跟踪分别用了1.9和1.6s,改进趋近律的非奇异终端滑模控制比非奇异终端滑模控制分别提前0.4和0.3s完成追踪;从图2a、图3c和图2b。由图2d可见,关节1的控制输出抖振范围分别为[-20,380]和[-15,175],关节2的控制输出抖振范围分别为[-170,250]和[-10,80],改进趋近律的NTSMC抖振范围明显小于NTSMC的抖振范围。因此,改进趋近律的NTSMC比NTSMC制轨迹跟踪速度快,而且改进趋近律的非奇异终端滑模控制器的输出抖振明显减小。 a 关节1 b 关节2 a 关节1 b 关节2 a 关节1跟踪曲线 b 关节2跟踪曲线 c 关节1输入曲线 d 关节2输入曲线 (1)分析了NTSMC中存在的问题,提出将切换函数和趋近律一同在控制器中进行设计,达到实时补偿的效果。 (2)设计自适应趋近律,明显减小了系统的抖振,并提高系统的跟踪速度,缩短了到达滑模面的时间。 (3)利用Lyapunov定理证明了基于改进趋近律的NTSMC的稳定性。 (4)通过仿真对比验证了文中方法的先进性。 [1]ZAK M. Terminal attractors in neural networks[J]. PhysicsLetters, 1989, 2(4): 259-274. [2]FENG Y, YU X H, MAN Z H. Non-singular terminal sliding mode control of rigid manipulators[J]. Automatica, 2002, 38(12): 2159-2167. [3]JIN M L, LEE J, HUN P. Practical nonsingular terminal sliding-mode control of robot manipulators for high-accuracy tracking control[J]. IEEE Trans on Industrial Electronics, 2009, 56(9): 3593-3601. [4]郑剑飞, 冯勇, 陆启良. 永磁同步电机的高阶终端滑模控制方法[J].控制理论与应用, 2009, 26(6): 697-700. [5]FENG Y, ZHENG J F, YU X H, etal. Hybrid terminal sliding mode observer design method for a permanent magnet synchronous motor control system[J]. IEEE Transon Industrial Electronics, 2009, 56(9): 3424-3431. [6]梅红, 王勇. 快速收敛的机器人滑模变结构控制[J].信息与控制, 2009, 38(5) : 552-557. [7]姜君, 陈庆伟, 郭健, 等. 基于新型趋近律的动中通系统滑模稳定跟踪控制[J].控制与决策,2011,26(12): 1904-1908. [8]朱齐丹, 吕开东, 李新飞, 等.一种基于改进趋近律的离散变结构控制方法[J].系统工程与电子技术, 2012, 34(6): 1211-1214. [9]孙彪, 孙秀霞. 一种新的趋近律离散滑模控制方法及仿真[J]. 系统仿真学报, 2010, 22(10): 2422-2425. [10]马克茂, 王子才, 张德成. 离散时间系统变结构控制的新方法[J]. 电机与控制学报, 2001, 5(3): 181-184. [11]KUO T C, HUANG Y J. Neural network global sliding mode PID control for robot manipulators[C]//Proceedings of the World Congress on Engineering. Cincinnati: WCEAM, 2007: 470-474.[12]RAVARI A R N, TAGHIRAD A H D. A novel hybrid fuzzy-PID controller for tracking control of robot manipulators[C]//Proceedings of the 2008IEEE International Conference on Robotics and Biomimertics.Piscataway,NJ,USA:IEEE,2009:1625-1630. [13]LEE M J.An adaptive tracking control for robotic manipulators based on RBFN[J]. International Journal of Fuzzy Logic and Intelligent Systems, 2007, 7(2): 96-101. [14]HA Q P, NGUYEN Q H, RYEETAL D C. A fuzzy sliding mode controllers with applications[J]. IEEE Transactions on Industrial Electronics, 2001, 48(1): 38-46. [15]HSU Y C, CHEN G, LI H X. A fuzzy adaptive avariable structure controller with applications to robot manipulators[J].IEEE Transactions on Systems,Man and Cybemetics: Part B, 2001, 31(3): 331-340. (编辑徐岩) Nonsingular terminal sliding mode control for manipulator based on improved reaching law XUJie1,CHAIFawu2 (1.School of Electronic & Information Engineering, Heilongjiang University of Science &Technology, Harbin 150022, China; 2.School of Electrical & Control Engineering,Heilongjiang University of Science & Technology, Harbin 150022, China) This paper proposes an adaptive treading law used to improve the slower convergence and vibration occurring in terminal sliding mode control system. The law working by the distance of the state variables from the equilibrium position enables an adaptive change in the reaching time speed and shortens reaching time while reducing system chattering and thus may find a use in non-singular terminal sliding mode control of manipulators. Simulation results show that the proposed algorithm capable of a faster track of the desired trajectory, with less chattering, may provide an effective improvement in the performance of an anthropomorphic finger. adaptive treading; terminal sliding mode control; manipulators 2016-02-26 徐杰(1964-),女,黑龙江省哈尔滨人,教授,研究方向:图像处理、控制理论与控制方法,E-mail:xuejie640101@163.com。 10.3969/j.issn.2095-7262.2016.02.017 TP13 2095-7262(2016)02-0192-05 A2 趋近律设计





3 控制律设计


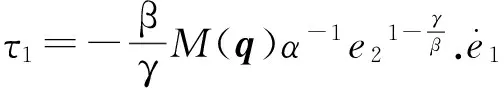


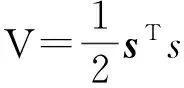





4 仿真设计


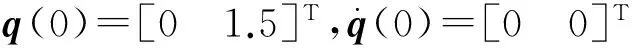





5 结 论

