加温过程中缺陷花岗岩的耦合损伤

高红梅,　兰永伟,　陈　勇,　李长凤

(1.黑龙江科技大学 建筑工程学院, 哈尔滨 150022； 2.黑龙江科技大学 矿业工程学院, 哈尔滨 150022)



加温过程中缺陷花岗岩的耦合损伤

高红梅1,兰永伟2,陈勇1,李长凤1

(1.黑龙江科技大学 建筑工程学院, 哈尔滨 150022； 2.黑龙江科技大学 矿业工程学院, 哈尔滨 150022)

为了能够正确评价温度作用下缺陷花岗岩的损伤机理，应用热力学、Maxwell应力理论，建立关于集中应力的非线性齐次微分方程，求解出花岗岩缺陷内部集中应力的表达式。采用应变等效原理，把缺陷花岗岩的受热状态分解成两种状态，即宏观缺陷的花岗岩受热状态和随机微观缺陷的花岗岩受热状态。全面分析了宏观裂纹花岗岩的受热过程中的损伤。细致研究内部微观随机性缺陷在受热作用下的损伤的耦合。推导了考虑宏、细观缺陷耦合的花岗岩复合损伤模量的计算公式。该理论推导公式可以为地热开发提供参考。

缺陷花岗岩； 宏观损伤； 微观损伤； 集中应力

0　引　言

天然花岗岩本身细观结构是由黑云母与石英、长石等晶粒组成的复杂混合体，花岗岩由于成岩过程和成岩环境的差异，都会随机地赋存一定的宏观和微观缺陷。这些天然缺陷或外界条件影响造成的缺陷，大大降低了花岗岩的力学性能，造成花岗岩力学性能的非连续性和均一性。花岗岩加热后，组成花岗岩的不同矿物颗粒膨胀系数不同，颗粒之间变形相互制约形成热应力。热应力会使得缺陷处出现应力集中现象，会使缺陷处颗粒出现损伤破坏，加速了花岗岩的破坏速度。因此，研究温度作用下缺陷花岗岩内部热应力、缺陷处应力集中变化情况，以及缺陷花岗岩在温度作用下耦合损伤，对于研究温度作用下缺陷花岗岩热破裂起到至关重要的作用。

国内外许多学者对完整的岩石热损伤及其破坏机制等方面进行了大量的研究。王鹏等[1]对不同温度作用后的砂岩试样进行损伤分析；高美奔[2]对岩样在温度上升引起热应力和围压不同情况下的破坏特征进行研究；肖旸[3]通过对煤岩体热处理后，对煤岩体裂纹宽度、煤岩体颜色等进行了实验扫描；冯子军等[4]利用高精度工业试验机进行了不同温度下褐煤、气煤细观结构演化的显微实验；张连英[5]采用泥岩作为实验对象，通过射波分析高温泥岩衍内部颗粒化学反应和损伤原因。赵贵杰[6]通过测得图像对试样孔隙、裂隙以及矿物颗粒的形态特征进行计算,分析温度对损伤的影响机理；张慧梅等[7]建立温度-荷载耦合作用下岩石的损伤模型，分析岩石细观损伤所诱发的宏观力学性能演化途径。于庆磊等[8]运用数值模型研究花岗岩在温度和压缩荷载共同作用下的力学行为和破裂过程。张吉宏[9]建立了基于变形元件的岩体损伤演化模型。吴渤等[10]对泥岩三轴压缩实验进行了一系列数值模拟。赵延林等[11]采用CY微段节理模型的细观剪切力学参数，探讨剪切作用下随机形貌岩石节理剪切-渗流响应。王春萍等[12]通过将高温损伤流变元件代替经典西原模型中 Newton 元件的方法，构建了能够描述不同温度条件下花岗岩蠕变全过程的本构模型。刘波等[13]根据μ和σ参数的大小来判断各参数对模型温度值输出影响情况，并分析岩体水-热模型的时空变化规律。贾善坡等[14]以泥岩损伤为主线，引入损伤变量，建立泥岩的渗流-损伤耦合模型，完成了有限元程序的二次开发。李新平等[15]研究岩体的损伤模式，从微观研究温度作用下岩石强度、损伤的规律。王利等[16]利用微裂纹尺度-频数分布分形作微裂纹粗糙表面分形研究。袁小清等[17]推导了考虑宏细观缺陷耦合的复合损伤变量，并给出同时考虑试件尺寸、裂隙几何与力学特性的宏观损伤变量的计算公式。张力民等[18]讨论了载荷应变率及节理条数对岩体动态力学特性的影响规律。

上述研究成果，由于研究设施的局限性，所以有关高温环境下缺陷岩石破坏损伤机理的研究文献较少。特别是缺陷花岗岩在温度作用下内部热应力、应力集中，缺陷损伤演化规律等问题，也正是近年来面临的新的问题。因此，研究缺陷花岗岩应力集中、缺陷损伤对花岗岩热破裂问题是重要的理论基础。

1　花岗岩缺陷处热应力的产生

花岗岩内含各种矿物结晶成分和微裂隙、微孔洞等初始缺陷的天然材料。在花岗岩受热过程中，晶体颗粒之间会产生相互的作用，颗粒之间的这种相互作用就是热应力[19]。

在缺陷花岗岩中取缺陷处进行研究，花岗岩裂纹缺陷见图1，受力分析如图2。

图1　花岗岩裂纹缺陷

花岗岩热应力关系为

σe=Eε-αβΔT，

(1)

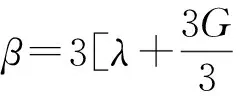
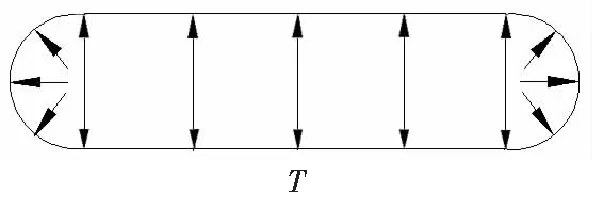
图2　温度作用下花岗岩缺陷处受力分析

Fig. 2Stressanalysisofgranitedefectsunder

actionoftemperature

花岗岩内部缺陷处集中应力表示为σloc，花岗岩因为缺陷引起的附加应力为Δσ。局部集中应力σloc可以表示为

σloc=σe+Δσ,

根据Maxwell应力模型，花岗岩缺陷处集中应力为

(2)

为了方便求解，将式(2)改写为

(3)

式(3)非线性齐次方程的通解

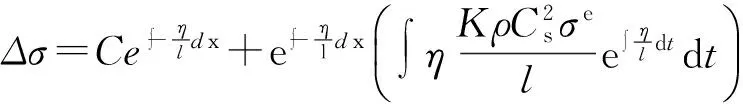
积分可得

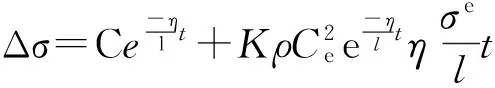
其中，dΔσ|t=0=0，得C=0。

则，缺陷处附加应力

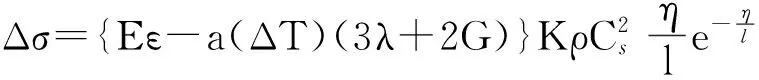
(4)

花岗岩缺陷处集中应力

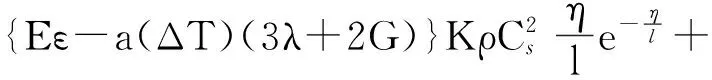
{Eε-aΔT(3λ+2G)}。

(5)

2　缺陷花岗岩损伤演化方程

花岗岩内部随机分布着各种细观缺陷，可将其内部种种缺陷视为随机损伤，从统计损伤力学的思想出发进行研究。它是将岩石内部损伤程度以微元强度加以量化，并根据岩石内部损伤服从随机分布的特点，假定岩石内部缺陷服从某种分布，进而建立相应的岩石统计损伤本构模型。

损伤耦合的条件是在一定应力作用下，两种损伤分别引起的损伤应变之和等于耦合损伤引起的应变[15]，即为Maxwell应力理论，如图3所示，假设图 3a～d分别为同时含有宏观和细观缺陷的岩体、仅含宏观缺陷的岩体、仅含细观缺陷的岩石和虚拟的完全不含损伤的岩石，其弹性模量分别为E′、E1、E2、E0，其在总温度应力σ作用下产生的应变分别为ε′、ε1、ε2、ε0，那么根据损伤耦合的条件，则有ε′=ε1+ε2-ε0,若假设宏、细观损伤在应力方向上造成的损伤分别为D′、D1、D2、D0，耦合损伤为

(6)

将式(6)代入式(5)，整理可得

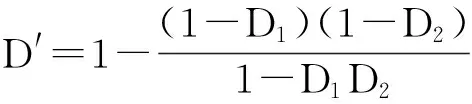
(7)

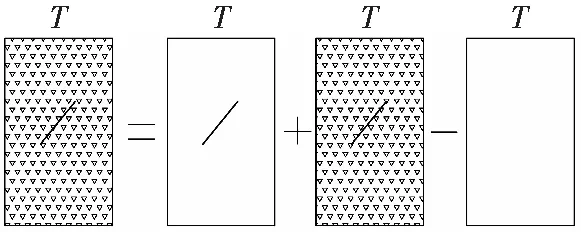
a　　　　b　　　　c　　　　d

图3b中在花岗岩弹性介质加温过程中存在缺陷处的应力为式(4)，整理可得

温度对缺陷花岗岩的损伤，热损伤变量D1

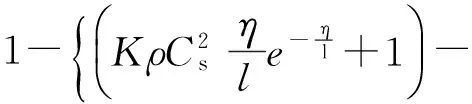
(8)

图3c中假定岩石微元强度服从双参数的Weibull分布，其概率密度函数为

(9)

式(9)中，花岗岩微观缺陷随机分布时的强度为p(ε)；花岗岩微观缺陷随机分布时的应变为ε；m,ε0为分布参数。

加热时花岗岩内部随机分布的缺陷扩展，演化成宏观的花岗岩热损伤，其损伤实际上随机分布微观缺陷损伤累计的效果，记作D2，表达式为

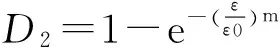
(10)

将式(8)和(10)代入式(7)，整理可得温度作用下缺陷花岗岩的损伤为

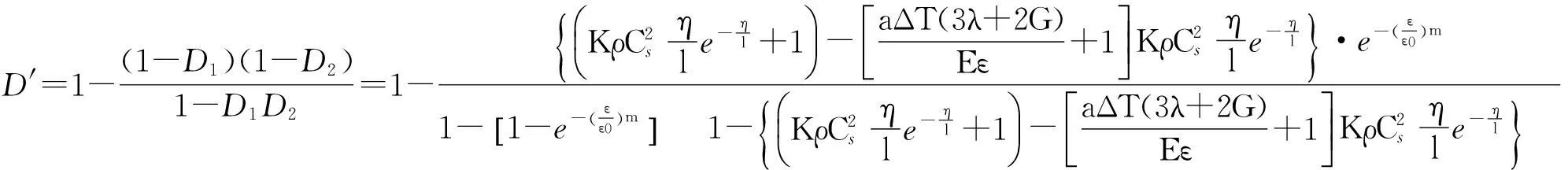
(11)

式(11)依据应变等效原理，考虑缺陷处集中应力存在，综合计算出宏观缺陷和细观内部随机性缺陷的花岗岩在受热作用下的损伤模量，进行两种状态下损伤模量的耦合，对于研究高温缺陷花岗岩的热破裂可以提供理论参考。

3　结　论

(1)在温度作用下，单裂隙缺陷花岗岩中会产生热应力，在花岗岩缺陷处会出现应力集中，随着温度升高，花岗岩的损伤程度会加剧。应用热力学理论、Maxwell应力理论，推导出花岗岩缺陷内部出现的拉应力的计算公式。缺陷内部的出现与集中应力和温度变化量、缺陷的长度、缺陷集中应力的扩大系数等有关。

(2)应用应变等效原理，把缺陷花岗岩的受热状态分解成两种状态，即宏观缺陷的花岗岩热状态和随机微观缺陷的花岗岩热状态。求解出存在宏观缺陷花岗岩的受热过程中的损伤模量，计算出细观内部随机性缺陷在受热作用下的损伤模量，进行两种状态下损伤模量的耦合，推导了花岗岩复合损伤模量的计算公式。

[1]王鹏, 许金余, 刘石, 等. 砂岩的高温损伤与模量分析[J]. 岩土力学, 2014, 35(增2): 2133-2139.

[2]高美奔. 热-力作用下硬岩本构模型及其初步运用研究[D]. 成都: 成都理工大学, 2014.

[3]肖旸. 煤田火区煤岩体裂隙渗流的热-流-固多场耦合力学特性研究[D]. 西安: 西安科技大学, 2013.

[4]冯子军, 赵阳升. 煤的热解破裂过程-孔裂隙演化的显微CT细观特征[J]. 煤炭学报, 2015, 40(1): 103-109.

[5]张连英. 高温作用下泥岩的损伤演化及破裂机理研究[D]. 北京: 中国矿业大学, 2012.

[6]赵贵杰. 油页岩热损伤演化特性及损伤模型研究[D]. 长春: 吉林大学, 2015.

[7]张慧梅, 杨更社. 冻融与荷载耦合作用下岩石损伤模型的研究[J]. 岩石力学与工程学报, 2010, 29(3): 472-478.

[8]于庆磊, 郑超, 杨天鸿, 等. 基于细观结构表征的岩石破裂热-力耦合模型及应用[J]. 岩石力学与工程学报, 2012, 31(1): 41-51.

[9]张吉宏. 综合考虑宏细观缺陷的岩体损伤本构模型及破坏机理研究[D]. 长春: 吉林大学, 2015.

[10]吴渤, 贾善坡, 高敏, 等. 岩石热-弹塑性-损伤耦合力学模型及其数值实施[J]. 合肥工业大学学报, 2015, 38(8): 1098-1105.

[11]赵延林, 万文, 王卫军, 等. 随机形貌岩石节理剪切-渗流数值模拟和剪胀-渗流模型[J]. 2013, 38(12): 2133-2139.[12]王春萍, 陈亮, 梁家玮, 等. 考虑温度影响的花岗岩蠕变全过程本构模型研究[J]. 岩土力学, 2014, 35(9): 2494-2502.

[13]刘波, 金爱兵, 高永涛, 等. 基于Morris法的单裂隙岩体温度场参数灵敏度分析[J]. 采矿与安全工程学报, 2016, 33(1): 153-159.

[14]贾善坡, 高敏, 于洪丹, 等. 高孔低渗泥岩渗流-损伤耦合模型与数值模拟[J]. 中南大学学报, 2016, 47(2): 559-569.

[15]李新平, 路亚妮, 王仰君. 冻融荷载耦合作用下单裂隙岩体损伤模型研究[J]. 岩石力学与工程学报, 2013, 32(11): 2308-2317.

[16]王利, 毛原春, 叶金生, 等. 基于微缺陷成核序列的岩石微裂纹生长和损伤演化模型[J]. 工程力学, 2013, 30(8): 278-287.[17]袁小清, 刘红岩, 刘京平. 基于宏细观损伤耦合的非贯通裂隙岩体本构模型[J]. 岩土力学, 2015, 36(10): 2805-2815.

[18]张力民, 吕淑然, 刘红岩. 综合考虑宏细观缺陷的岩体动态损伤本构模型[J]. 爆炸与冲击, 2015, 35(3): 428-436.

[19]唐世斌, 唐春安, 朱万成, 等. 热应力作用下的岩石破裂过程分析[J]. 岩石力学与工程学报, 2006, 10 (25): 2071-2079.

(编辑徐岩)

Study on coupled damage of defect of granite during continuous heating

GAOHongmei1,LANYongwei2,CHENYong1,LIChangfeng1

(1.School of Civil Engineering, Heilongjiang University of Science & Technology， Harbin 150022, China;2.School of Mining Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)

This paper is an effort to enable a correct evaluation of the damage mechanism behind defective granites. This paper is focused on the application of the theory of thermodynamics and Maxwell’s stress to establish Non-linear homogeneous differential equation about the concentrated stress and solution to the expression of concentrated stress near the defect of granite. The study building on using the strain equivalence principle involves decomposing thermal state of the defects of granite into two states, namely, the thermal state of granite with the macroscopic defects and the thermal state of granite with random micro-defects; completely analyzing the coupled damage of macroscopic defects of granite and random defects under the action of heat; and developing the calculation formula of the composite damage with considered the macro and micro coupled defects of granite. The theoretical derivation formula could provide a theoretical reference to the study of geothermal exploration.

defect of granite; macro-damage; micro-damage; concentrated stress

2016-06-01

黑龙江省青年科学基金项目(QC2014C062)；国家自然科学基金青年科学基金项目(11402080)

高红梅(1978-)，女，山西省吕梁人，副教授，硕士，研究方向：高温岩石渗流，E-mail:85289703@qq.com。

10.3969/j.issn.2095-7262.2016.04.016

TU452

2095-7262(2016)04-0429-04

A