Marangoni效应对降膜流动影响的模拟研究

全晓宇，耿 洋，孙 博黄哲庆刘春江

（1. 天津大学化工学院，天津 300072；2. 化学工程联合国家重点实验室（天津大学），天津 300072；3. 天津化学化工协同创新中心，天津 300072）

Marangoni效应对降膜流动影响的模拟研究

全晓宇1，2，3，耿 洋1，2，3，孙 博2，黄哲庆2，刘春江1，2，3

（1. 天津大学化工学院，天津 300072；2. 化学工程联合国家重点实验室（天津大学），天津 300072；3. 天津化学化工协同创新中心，天津 300072）

采用计算流体力学的方法，提出了1个三维模型来研究竖直板上受热和受冷降膜的Marangoni效应对降膜流动的影响，得到了液膜表面温度、速度、涡量以及润湿面积比等参数随时间变化关系.模拟结果表明，液膜受冷其润湿面积增大，受热收缩.Marangoni效应在液膜的水平方向表现得更加明显，受热液膜径向修正 Marangoni数为轴向修正Marangoni数的8倍.受热液膜表面波动加强，边缘处涡量增大，而液膜主体流向速度由于受到液膜收缩的影响也增大.

Marangoni效应；降膜流动；计算流体力学

降膜流动传热设备具有高效的传热传质系数、小温差、高热流密度、低能耗的特点，被广泛应用于精馏、降膜蒸发以及海水淡化等工业生产过程中［1］. 研究发现，非等温降膜过程中，流体的流型发生显著变化，从而对传热传质产生影响［2］.在降膜的传热传质过程中，液膜表面温度的不均匀分布会产生表面张力梯度，在液膜表面切线方向产生剪应力，即 Marangoni剪应力，进而在液膜表面引发热毛细对流，也就是Marangoni效应.受热降膜产生的Marangoni剪应力引起液膜收缩，受冷降膜产生的Marangoni剪应力促使液膜更容易铺展.然而，在实际传热传质过程中，由于 Marangoni剪应力比流体惯性力小得多，且只存在于流体界面，因而常常被忽略［3］. 但后期随着对于降膜流动传热微观机理的不断研究，发现降膜传热传质系数的变化与Marangoni效应具有重要关系［4］.因此，通过实验和数值模拟来研究降膜流动过程中Marangoni效应的产生和作用机理，对于提高降膜设备传热传质效率有重大的实际意义.

Kapitza等［5］最早开始研究热 Marangoni效应所引起的界面现象.在此之后，有众多学者通过实验和数值模拟研究了液膜热毛细不稳定现象.张锋等［6］以蒸馏水为介质，采用红外热像仪和智能化薄膜厚度测试仪，研究竖直板上受热降膜的流动特性.研究发现，受热降膜在流动过程中横向存在很大的温度梯度，从而引发很强的热 Marangoni效应，使得液膜整体向中央主流区收缩，导致液膜润湿面积减小；并且加热温差越大，由此而导致的液膜表面温度梯度和表面张力梯度较大，液膜收缩更为明显.Zhang等［7］在后期的研究中引入液膜收缩角，以此考察壁面温度、流量、固液接触角对液膜分布的影响以及受热降膜的温度分布，建立了竖直板上受热降膜收缩特性的模型.随后赵贤广等［8］又通过进一步实验研究，提出采用修正的 Marangoni数和 Marangoni效应影响因子描述Marangoni效应对液膜流动的影响程度，更好地表征了Marangoni效应对于降膜流动的影响.Séamus等［9］采用稳态数值模拟的方法研究了无重力条件下平板加热引起的气泡Marangoni热效应，模拟结果表明在气泡周围发生明显的对流，并且在气泡底部边缘热通量提高1倍.

笔者采用 CFD的方法，将表面张力随温度的变化添加进计算模型，以 VOF计算方法为基础，采用三维计算模型，对有限宽度的受热以及受冷降膜流动过程进行了模拟研究，分析液膜在不同受热或受冷温差条件下的温度、速度和涡量分布，以及在不同时刻下的润湿面积变化，研究了Marangoni热效应对降膜流动的影响，为降膜设备的设计提供了理论依据.

1　数值模拟

1.1物理模型

文中模拟对象为三维平板上的降膜流动过程，如图1所示.该降膜流动结构为长50，mm（x方向）、宽10，mm（y方向）、高 120，mm（z方向）的长方体，其中点O为坐标原点.液相进口宽1，mm，长30，mm，位于长方体顶端靠近壁面，靠近液相进口一侧为不锈钢壁面，上部20，mm为恒温壁面，下部100，mm为加热（冷却）壁面.对于模型中的进口均采用速度进口，出口采用压力出口.液体在壁面上形成液膜，在流经下方壁面后由于受到加热（冷却）板的加热（冷却），在液膜表面产生Marangoni剪应力，并在该剪应力的影响下液膜会发生收缩（扩展），最后液膜从长方体底部液相出口流出.

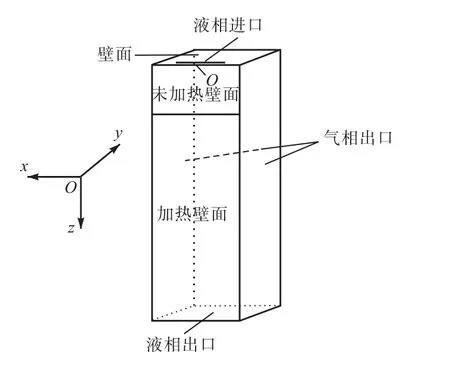
图1　三维降膜流动物理模型Fig.1　Physical configuration of the 3D falling liquid film flow model

由于液膜在壁面流动时间很短，温度较低，为了简化计算，液体蒸发在计算中忽略不计.模拟中选用空气-水作为物料，其性质见表1.

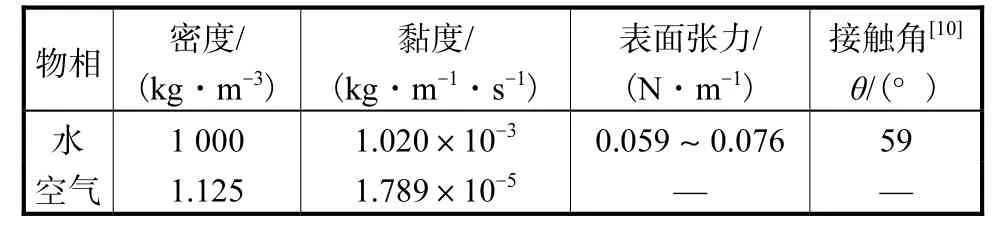
表1　空气-水的物性参数Tab.1 Properties of air-water system

1.2数学模型

平板上的降膜流动过程属于非稳态气-液两相分层流动过程.为确定波动液膜的自由表面位置，选用VOF（volume of fluid）界面追踪技术进行模拟.当计算单元被液相充满时，液相体积分数为 1，被气相充满时，液相体积分数为 0.当液相体积分数在 0到 1之间时，可认为该位置为气液相界面.

1.2.1控制方程连续性方程为

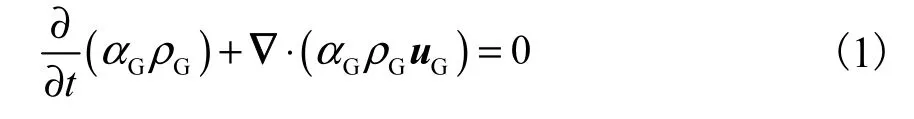
式中：αG为气相体积分数；ρG为气相密度.则液相体积分数计算式为

在 VOF模型当中，气液两相共用一套动量方程，即

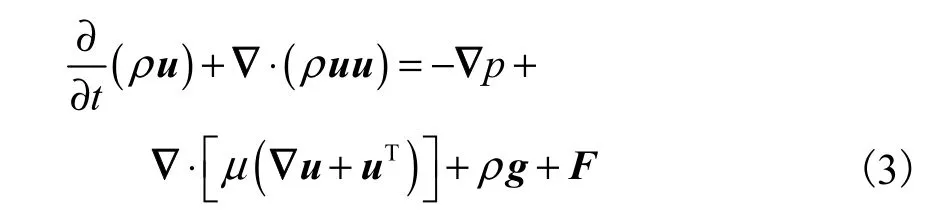
能量方程为

式中：cp为流体的比定压热容；a为流体的分子热扩散系数；t为流体温度；Q为热量输运方程的源项，由于流体无热源，故在此Q为0.

控制方程中流体的物理参数由每个控制体内各相共同决定，对于气-液两相流，每个控制体内的密度ρ和黏度μ可由以下两式给出：

1.2.2动量源项的确定

式（3）中的 F表示动量源项，包括表面张力动量源项FVOL和Marangoni剪应力动量源项FMa两部分.

表面张力动量源项 FVOL根据 Brackbill等［11］提出的模型可表示为

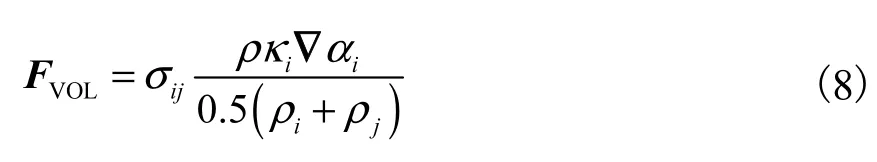
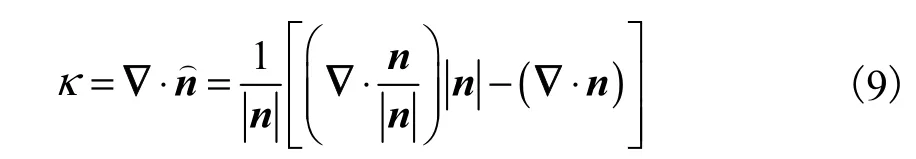
γw为壁面处的固液接触角，则壁面处的单位曲面法向量为

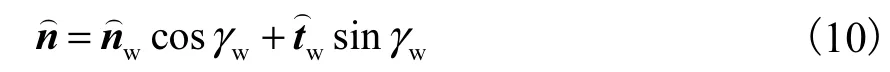
当界面处存在温度或浓度梯度时，会产生表面张力梯度，表面张力梯度对流体界面流动的影响可用Marangoni剪应力来表示.Cazabat等［12］最早描述了温度梯度引起的 Marangoni剪应力对静止流体的影响.Marangoni剪应力动量源项表示为

式中：σ为表面张力；∇ t为温度梯度.根据图2［13］可知，dσ/dt符合线性规律，可以设其为常数-1.72× 10-4.因此式（11）可简化为

图2　水的表面张力随温度的变化Fig.2　Change of surface tension of water with temperature

1.3网格划分

网格的划分方法如图3所示，模拟过程全部采用精度较高的四边形网格.本文分别采用 4种不同网格数量的模型进行模拟，并与文献［8］进行了比较，见图4.其中 ReL为进口处液相雷诺数，tin为液相进料温度，twall为加热壁面温度.从图4中可以看出，随着网格数量的增多，网格不断细化，模拟结果与实验结果趋于接近.当网格数量分别为 99，360和 198，720时，液相出口温度基本不再变化，但计算量却相差 1倍，因此本文选用网格数为99，360的计算模型.计算域长度以及宽度范围内相邻网格之间网格大小采用不同的比例因子不断增大或减小，具体网格划分细节见表2.

图3　计算域内的网格划分Fig.3 Mesh generation in calculation region

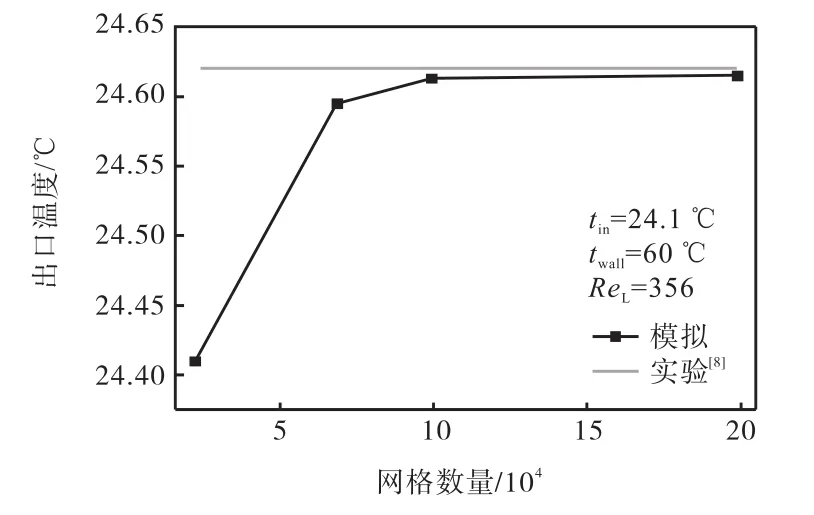
图4　模拟结果随网格数量的变化Fig.4 Change of simulation data with grid number

表2　计算域网格的配制信息Tab.2 Mesh allocations for the calculation region

1.4数值计算方法

计算软件选用 FLUENT 6.3软件包，并采用FLUENT自带前处理软件GAMBIT 2.4对几何物理模型进行网格划分，然后将网格文件导入 FLUENT求解器中进行计算求解.离散时间项采用隐格式，对流项采用一阶迎风格式，压力项采用 Body Force Weighted算法，压力-速度耦合方程采用SIMPLIC算法，时间步长在10-4～10-5，s之间选取，可根据具体计算情况选定.气、液相界面追踪采用 VOF和几何重构（geometric reconstruction）方法.图5中为 x=0,mm时，计算过程中气液界面云图的剖面图，从图中可以看出，气液界面较为平稳清晰，但存在轻微的波动.在计算中，首先计算了未加热时的流动状况，在其稳定后，时间为 1，s，对加热板进行加热，时间为2，s时达到稳定状态，故文中的稳态结果均是计算时间为2，s时的结果.

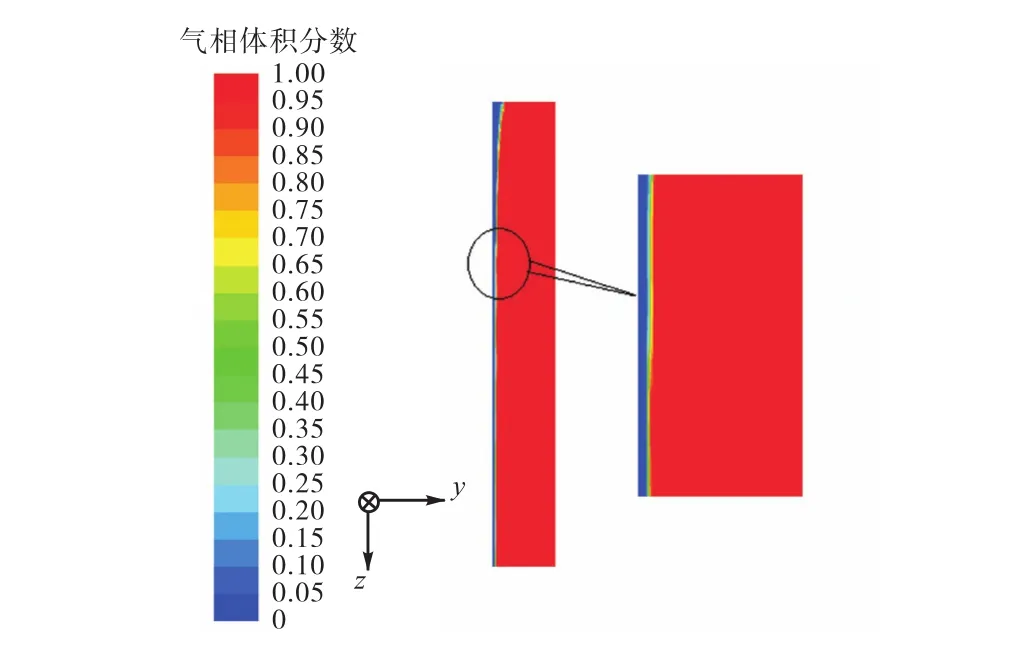
图5　气液界面云图Fig.5 Profile of gas-liquid interface

2　Marangoni效应对降膜流动的影响分析讨论

2.1受热降膜温度分布

由于 VOF模型中，在不同相中是以一组能量方程计算，故以气液接触面作为液相表面温度，再做平均得到表面流向温度.图6为受热降膜表面的流向温度分布，将本文模拟结果与文献［8］中的实验结果进行比较，横坐标 z=20，mm以后为加热区域.从图6中可以看出，在降膜流向中，随着液膜向下流动，液膜表面的温度逐渐升高.模拟结果与实验值基本接近，因此本文提出的 CFD模型能够较为准确地模拟降膜过程中的液膜温度变化.

图6　受热降膜表面流向温度分布Fig.6　Temperature distribution of liquid film in streamwise direction

图7为出口处径向液膜厚度和温度分布.由图7可知，液膜边缘表面温度明显高于中心区域液膜表面温度，存在较大的温度梯度，而中央主流区域液膜温度分布较为均匀，这主要由于液膜边缘较薄，中间厚度较大，边缘处更容易被加热而呈现较大的温度梯度. 由于水的表面张力随着温度的升高而降低，在液膜流向和径向上产生了与液膜流动相反的表面张力梯度，因此也产生了与液膜流动相反的热毛细流动.因此，在液膜径向和流向上都存在 Marangoni效应.Ehrard等［14］认为，水平板上受热液滴的扩展主要由重力、表面张力和 Marangoni效应来决定.在受热竖直板降膜过程中，其主体流动方向向下，重力的影响较为显著，Marangoni效应较弱，径向上由于重力作用降低，液膜径向流动主要受 Marangoni效应控制，使液膜收缩.

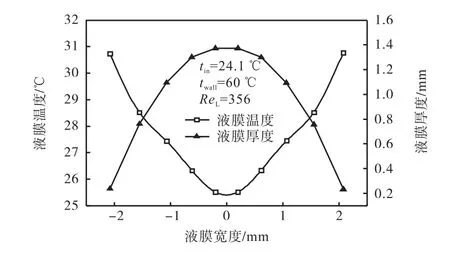
图7　受热降膜表面径向温度分布Fig.7　Temperature distribution of liquid film in transverse direction

2.2降膜流动的Marangoni数

非等温降膜过程中通常利用 Marangoni数来表征温度引起的表面张力梯度对降膜流型的影响［15］，其定义如下：

图8为径向 Marangoni数随液相流量和壁面温差的关系.如图所示，由于为负值，对于受热液膜而言，径向 Marangoni数为负值，对于受冷液膜正好相反.受热液膜受温差的影响比较显著，随着加热温差的增大，减小，说明温差越大，径向Marangoni效应越显著.温差增大导致液膜表面分布不均程度增大，从而导致表面张力梯度增大，进而增大了 Marangoni效应.液相流量对于也有一定的影响，随着ReL的增大，先减小后增大.当ReL＜200时，由于液相流量小，壁温随流量变化不明显，而受热液膜温度随液相流量的增大而降低，导致加热板和液膜间温差增大，相应减小.当 ReL＞200时，由于液相流速的增大导致液相与加热板表面更新加快，加热板表面温度降低，因此加热板和液相温差减小，增大.受冷液膜变化趋势和受热液膜正好相反.

图8　流量和温差对?的影响Fig.8 Influence of liquid phase flow rate and temperature difference on

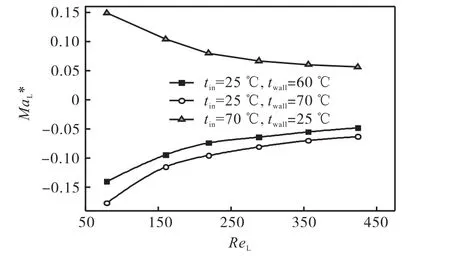
图9　流量和温差对的影响Fig.9　Influence of liquidphase flow rate and temperature difference on

2.3降膜润湿面积比

降膜润湿面积比是指降膜板上液体润湿面积与降膜板面积之比.图10显示的是不同液相流量、不同时刻下的润湿面积比变化曲线.图中时刻1，s之前未对加热板加热，液膜恒温，1，s后对给定加热板一恒定温度，液膜受热.从图中可以看出，不同流量下的液膜在加热后其润湿面积比都变小，并且 Marangoni效应对于小流量下的液膜润湿面积影响比较显著.在 Re=79时，液膜受热后液膜表面波动比较剧烈，润湿面积比变化显著，而在大流量下，因 Marangoni效应对液膜的波动性影响较少，此时润湿面积主要受流量影响，液膜本身的润湿面积比变化并不显著.

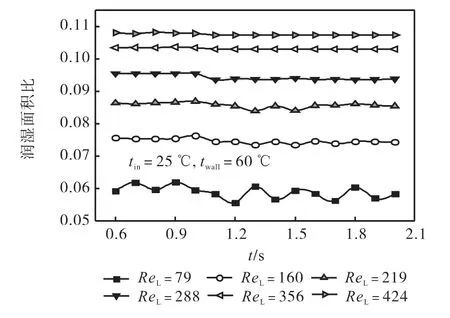
图10　流量对润湿面积比的影响Fig.10 Influence of liquid phase flow rate on wetting ratio

竖直平板上非等温液膜的润湿面积主要由表面张力梯度产生的 Marangoni效应及液体流速控制. Marangoni效应阻碍受热液膜的径向铺展，而液体流速增加有利于受热液膜的铺展.图11是液膜润湿面积比随着液相雷诺数和加热板温度的变化曲线.从图中可以看出，随着加热板温度的升高，液膜收缩加剧，润湿面积比减小，随着液相流量的增大，润湿面积比增大.在小流量下，Marangoni效应作用较强，使得液膜产生较大的收缩，当液相 ReL＞300时，Marangoni效应对于液膜的影响减小，而流量的扩展作用逐渐增强，表现为液膜润湿面积主要受流量的影响，不同温差下液膜润湿面积比基本相同.

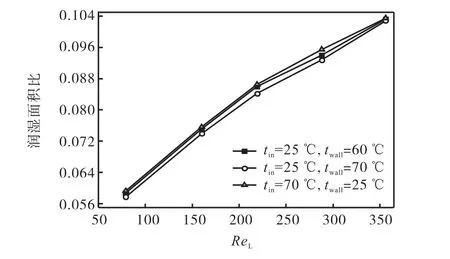
图11　不同加热板温度下液膜润湿面积比随液相雷诺数的变化Fig.11 Change of wetting ratio with ReLat different wall temperatures

2.4受热液膜涡量分析

在得到流场速度的情况下，即可求解流场中各点的涡量.涡量是由流场内一点流体质点的角速度所定义的，其大小代表了流场中各点旋度的大小，涡量大说明流体微团的旋转角速度大，流场扰动剧烈，有利于强化传质.由于液膜径向存在较大的温度梯度，因此，Marangoni效应所引起的液膜扰动主要集中在垂直于液膜流动平面.此平面上的涡量（rot）定义为

图12为由加热引起的Marangoni剪应力对出口液膜涡量的影响.从图中可以看出，不论加热与否，在液膜两侧涡量值较大，中间涡量较小，这主要由于液膜边缘处速度较大，且波动较为剧烈，而液膜中部流动相对稳定.当对液膜流经壁面进行加热时，由于液膜两侧厚度较薄，温度梯度较大，因此液膜两侧Marangoni效应更为显著，两侧的液体向中间收缩，表现为液膜两侧涡量增大，液膜变得不稳定.而液膜内部受到来自表面的 Marangoni剪应力影响较小，与未对壁面进行加热的液膜内部涡量值相差不大.

图12　不同加热条件对液膜出口涡量的影响Fig.12　Influence of heating conditions on vorticity of liquid film at outlet

2.5受热液膜速度分析

图13（a）～（d）是不同流动条件下出口处（x=0,mm，z=120,mm）液相沿 z方向速度分布的模拟结果，其中为液膜厚度.从图13中可以看出，几乎在所有的流动条件下，uz在靠近壁面处较小，远离壁面处较大，并在接近气液界面处速度达到最大.在小液相雷诺数下，不同加热板温度液膜在 z方向的速度分布存在明显不同，随着加热板温度的升高，相同位置处uz逐渐增大.由于模拟过程中水的黏度恒定，因此排除了黏度对液膜流速的影响.壁面温度影响 uz的原因主要有以下两方面：一方面较高的加热板温度增大了液膜表面到加热板之间的温度梯度，Marangoni剪应力增大，液膜收缩加剧，在通量一定的条件下液相流过面积的减小必然导致流速的增大；另一方面，这与水的表面张力在低温时较大、高温时较小有关，较小的表面张力有利于液膜更好地润湿加热平板，提高流动性，并且有助于提高传热效率.

在较高液相雷诺数下，不同加热板温度下的 uz相差并不明显，当 ReL=356时，3种流动条件下的uz基本相同，壁温的影响微乎其微.这主要是由于当液相流速增大时，液膜内部更新速率加快，抑制了液膜更大的温度梯度的形成，同时，由于液膜流速增大，惯性力也随之增大，但影响其流动的 Marangoni剪应力并未得到提高，因此很难再对流场产生较明显的影响.

图14是不同流量和温度下 x方向出口速度分布. 由图可以看出，降膜液相流过加热的降膜板时，液膜边缘沿x方向速度远远大于中心处速度，说明液膜在边缘有中心处收缩的趋势.对比图14（a）与14（b），可发现在不同的壁温下，图14（a）液膜边缘速度较大，液膜宽度较小，说明降膜液相与加热壁面温差越大，收缩程度越大，Marangoni现象越明显；对比图14（a）与 14（c），在大流量下，液膜边缘速度下降，液膜宽度增大，说明流量增大，收缩程度变小，Marangoni效应影响变小.

图13　不同温度下液膜z方向速度分布Fig.13 Velocity profiles in z direction at outlet at different temperatures

图14　不同温度和流量下x方向出口速度分布Fig.14　Velocity profiles in x direction at outlet with different flow rates and at different temperatures

3　结　论

本文通过FLUENT模拟分析了受热以及受冷液膜表面的温度、速度、涡量分布以及润湿面积比等，探究了非等温条件下，由表面张力梯度引发的Marangoni热效应对降膜流动的影响，结论如下.

（1） Marangoni效应在受热液膜的径向表现较为明显，阻碍液膜铺展，使其向中心收缩.Marangoni效应与受热温差和液体流速有关，液相流量小时，加热温差越大，液膜收缩越明显，而且液膜表面波动越剧烈；而当液相流量较大时，Marangoni效应对于液膜收缩影响较小，其润湿面积比变化不明显.

（2） 受热液膜由于 Marangoni效应导致其边缘处涡量增大，湍动增强，并向液膜中部扩展，大流量下受热液膜边缘涡量也有所增大，但对液膜中部的影响较小.

（3） 受热液膜径向和展向边缘处因 Marangoni效应的扰动作用导致其速度增大，而在流向上，由于此时Marangoni剪应力方向与液膜流动方向相反，导致其边缘处速度减小，部分流体向中间集中，又促进了主体处流速的增大.

［1］ 汪磊磊，由世俊，王书中，等. 水平管间溴化锂溶液滴状降膜流动分析［J］. 天津大学学报，2010，43（1）：37-42. Wang Leilei，You Shijun，Wang Shuzhong，et al. Analysis of LiBr solution droplet falling film flow between horizontal tubes ［J］. Journal of Tianjin University，2010，43（1）：37-42（in Chinese）.

［2］ Asim M，Anandamoy M. Nonlinear stability of viscous film flowing down an inclined plane with linear temperature variation ［J］. Journal of Physics D：Applied Physics，2007，40（8）：5683-5690.

［3］ 阎维平，叶学民，李洪涛. 液体薄膜流的流动和传热特性［J］. 华北电力大学学报，2005，32（1）：59-65. Yan Weiping，Ye Xuemin，Li Hongtao. Hydrodynamics and heat transfer of liquid thin films ［J］. Journal of North China Electric Power University，2005，32（1）：59-65（in Chinese）.

［4］ Kabov O A，Chinnov F A. Heat transfer from a local heat source to subcooled liquid film ［J］. High Temperature，2001，3（5）：703-713.

［5］ Kapitza P L，Kapitza S P. Wave flow of thin layers of a viscous fluid ［J］. Zh Eksp Teor Fiz，1949，19（2）：105-120.

［6］ 张 锋，耿 皎，赵贤广，等. 红外热像法研究降膜流动［J］. 化工进展，2006，25（10）：1188-1192. Zhang Feng，Geng Jiao，Zhao Xianguang，et al. Thermal imaging study of falling liquid films ［J］. Chemical Industry and Engineering Progress，2006，25（10）：1188-1192（in Chinese）.

［7］ Zhang F，Zhang Z B，Geng J. Study on shrinkage characteristics of heated falling liquid films ［J］. AIChE Journal，2005，51（11）：2899-2907.

［8］ 赵贤广，张志柄. 受热降膜 Marangoni效应临界状态表征［J］. 化工时刊，2010，24（12）：1-6. Zhao Xianguang，Zhang Zhibing. Characteristic of the threshold of Marangoni effect on heated falling film ［J］. Chemical Industry Times，2010，24（12）：1-6（in Chinese）.

［9］ Séamus M O S，Anthony J R. Numerical investigation of bobble-induced Marangoni convection ［J］. Interdisciplinary Transport Phenomena，2009，1161（1）：304-320.

［10］ Nicolaiewsky E M A，Fair J R. Liquid flow over textured surfaces. 1. Contact angles［J］. Ind Eng Chem Res，1999，38（1）：284-291.

［11］ Brackbill J U，Kothe D B，Zemach C. A continuum method for modeling surface tension ［J］. Journal of Computational Physics，1992，100（2）：335-354.

［12］ Cazabat A M，Heslot F，Troian S M，et al. Fingering instability of thin spreading films driven by temperature gradients ［J］. Nature，1990，346（628）：824-826.

［13］ Surface Tension of Water in Contact with Air［EB/OL］. http：//www.engineeringtoolbox.com/water-surfacetension-d_597. html，2011-10-27.

［14］ Ehrard P，Davis S H. Non-isothermal spreading of liquid drops on horizontal plates ［J］. Journal of Fluid Mechanics，1991，229（8）：365-388.

［15］ Kabov O A，Chinnor E A. Heat transfer from a local heat source to subcooled liquid film［J］. High Temperature，2001，39（5）：703-713.

（责任编辑：田 军）

Simulation of Marangoni Effect on Falling Liquid Film Flow

Quan Xiaoyu1，2，3，Geng Yang1，2，3，Sun Bo2，Huang Zheqing2，Liu Chunjiang1，2，3
（1.School of Chemical Engineering and Technology，，Tianjin 300072，China；2.State Key Laboratory of Chemical Engineering （Tianjin University），Tianjin 300072，China；3.Collaborative Innovation Center of Chemical Science and Engineering（Tianjin），Tianjin 300072，China）

Marangoni effect induced by temperature gradient is introduced into a three-dimensional computational fluid dynamics（CFD）model to investigate the hydrodynamic characteristics of the heated or cooled falling liquid films flowing down along a vertical flat plate.The parameters of temperature，velocity，vorticity and wetting ratio are obtained.It is found that the wetting ratio of the falling film increases when it is cooled and decreases when heated.Marangoni effect on the transverse direction of the falling liquid film is the main influence factor，and the radial modified Marangoni number is 7 times larger than the axial modified Marangoni number.It shows that the surface of the falling film is more unstable and the vorticity at the edge of heated falling film increases.Moreover，the velocity of the main body also increases due to the shrinkage of film.

Marangoni effect；falling liquid film flow；computational fluid dynamics

TQ021.1

A

0493-2137（2016）08-0809-08

10.11784/tdxbz201502014

2015-02-09；

2015-06-03.

国家重点基础研究发展计划（973计划）资助项目（2012CB720500）.

全晓宇（1988— ），男，博士研究生，quanxiaoyu@tju.edu.cn.

刘春江，cjliu@tju.edu.cn.

网络出版时间：2015-07-14. 网络出版地址：http://www.cnki.net/kcms/detail/12.1127.N.20150714.1124.001.html.