基于L-M方法的6R机器人轨迹规划快速逆解算法

邹丽梅，郭 波，钱学毅

（武夷学院 机电工程学院，武夷山 354300）

基于L-M方法的6R机器人轨迹规划快速逆解算法

邹丽梅，郭 波，钱学毅

（武夷学院 机电工程学院，武夷山 354300）

应用Denavit-Hartenberg建模方法，建立6R机器人正运动学模型，组成非线性方程组，提出运用Levenberg-Marquardt方法，求取机器人运动学逆解。利用MATLAB编程环境，实现轨迹规划位置逆解算法。经仿真验证，算法可完成复杂的轨迹轮廓规划逆解求解，有较高的效率和精度，可应用于一般6R机器人，也可适用自由度冗余更高的工业机器人。

Levenberg-Marquardt方法；工业机器人；轨迹规划；逆解；非线性方程组；

0　引言

机器人高效求运动学逆解算法开发一直是机器人运动学领域的热点问题，是实现机器人运动控制和轨迹规划的基础。当前常见6R工业机器人是典型带约束的多输入输出非线性系统，关节运动相互关联耦合，传统逆解求法将已知机器人末端位姿矩阵逐个左乘齐次变换矩阵逆阵，循序解出各关节角度值。求解过程不仅涉及矩阵求逆的复杂运算，且可能的逆解组合上限多达16组实数［1］，先求出的关节角度不适用机器人预期位姿时，求解过程就得重试，因此缺陷较多。近年发展的求逆解算法有两类，第一类是利用仿生智能算法直接在关节角解空间寻优或者搜索位姿矩阵与解空间的映射关系。吴振宇等建立优化算法的目标函数，在粒子群算法中引入遗传操作求解问题属于前者［2］。陈桂等应用优化的BP神经网络进行逆运动学求解属于后者［3］。仿生智能算法实现简单精度较高，但求解速度慢。运动学逆解答案不唯一，仿生智能寻优转变为复杂的多目标带约束优化问题，易陷入局部最优。第二类是分解齐次变换矩阵，构造非线性逆运动学方程，求解方程的根获得逆解。LEE等提出传统求逆问题可构造为一元16次方程求根问题。刘松国等对其求逆解法予以化简改进，提高了算法精度与速度［4］。钱东海等提出利用旋量法建立机器人运动学模型，得到6R工业机器人逆解显式解析式。吕世增、陈庆诚等［5，6］对其模型与子问题算法予以改进，增强适用性。构造非线性方程组求逆解计算效率高，可一次计算获得运动学全解，但方程物理意义不明显，构造困难。

本文提出利用物理意义明确的机器人运动学Denavit-Hartenberg建模方法，简称D-H法，获得一般6R工业机器人正运动学位姿矩阵。根据一般6R工业机器人最后3个关节为旋转关节而且轴线相交于一点［7］，其前3个关节决定末端执行器的位置构建为位置相关非线性方程组，后3个关节决定末端执行器的姿态构建为姿态相关方程组。先后分别以Levenberg-Marquardt方法，简称L-M方法，实现最小二乘迭代求解，实现高效率的逆解运算，获得较高的计算精度。

1　一般6R机器人逆运动学方程

以某焊接生产线用6R工业机器人为例，建立D-H坐标系如图1所示［8］。相应连杆参数如表1所示。

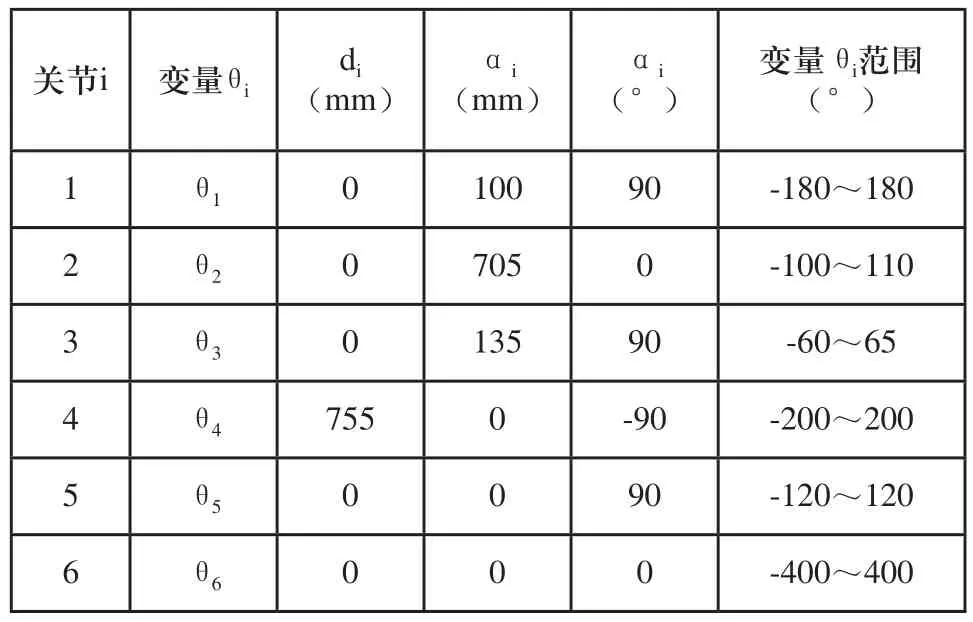
表1　6R工业机器人连杆D-H参数

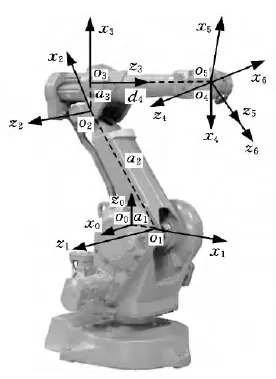
图1　6R工业机器人D-H坐标系定义

表1中任何一个连杆i，两端有关节i和i+1，两个关节轴线沿公垂线的距离αi为连杆长度；αi是在垂直αi的平面内两个轴线的夹角，即连杆扭角；di是沿关节i轴线的两个公垂线的距离；θi是垂直于关节i轴线的平面内两公垂线的夹角。

记Tii-1为从第i-1个坐标系到第个i坐标系的齐次变换矩阵，根据运动学正解的定义，6R机器人末端相对基座坐标系的位姿矩阵可表示为式（1）。

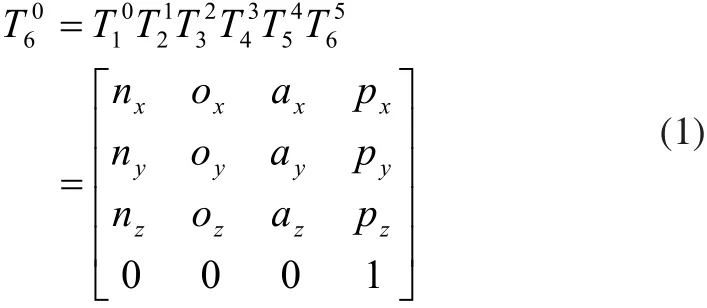
式中，N=（nx，ny，nz）T为末端执行器的法向矢量；O=（ox，oy，oz）T为末端执行器的端面矢量；A=（ax，ay，az）T为末端执行器的逼近矢量；P=（px，py，pz）T为末端执行器的中心位置矢量，均有明确的物理意义。

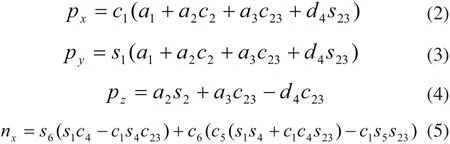
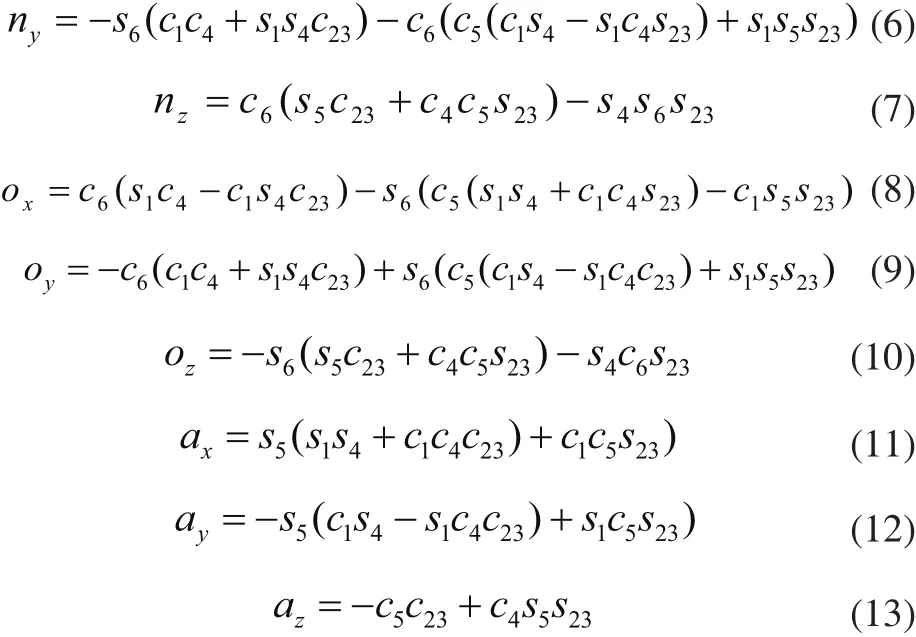
由式（2）～式（4）可知，位置矢量P=（px，py，pz）T仅与前三个关节角有关，可构成变量为θ1、θ2、θ3的三元非线性方程组。前三个关节角确定后，由式（5）～式（13）可构成求解执行器姿态的三元非线性方程组。

2　L-M方法求非线性方程组逆解

2.1Levenberg-Marquardt方法

机器人D-H法建模获得运动学方程为三角函数相关非线性方程，不存在求根公式，难以获得精确数值解，一般通过逼近求取近似解。为实现机器人高速精确的轨迹控制，求解方法必须有足够的精度以及速度。机器人末端执行器沿预定轨迹运动时，所需各关节角度变量是唯一且应平滑过渡，逆解算法需实现该目标。

Levenberg-Marquardt方法是由Levenberg（1944）［9］和Marquardt（1963）［10］提出的最小二乘问题求解方法，是对Gauss-Newton法的一种修正。为了防止非线性最小二乘问题求解中Jacobian阵奇异或接近奇异时试探步过长，通过求解方程组：

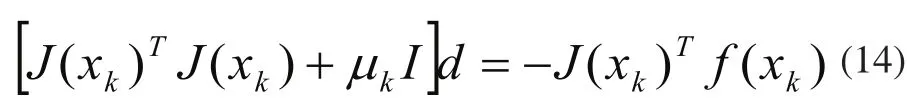
得到，下一个迭代点xk+1=xk+d。比例系数μk是一个正数，当μk=0时，L-M方法等同于Gauss-Newton法；当μk取值很大，L-M方法接近梯度下降法，μk随着迭代成功不断减少。

算法实现步骤：1）初始化给定方程f（x）、给定关节角θ初值、步长μk初值、步长放大系数α、步长缩小系数β、终止参数ε。2）求解式（14）获得d。3）当则令并返回2）步。4）令迭代终止，否则返回2）步。实践证明，L-M方法收敛速度远优于梯度下降法，适用于全局目标收敛，收敛位置较为依赖给定的初值。

2.26R机器人轨迹规划逆解算法设计

工业机器人轨迹规划是指以末端执行器的的初始位姿和用户给定的目标位姿，按预定轨迹运动过程中，确定每个关节角的位置与速度参数。基本分为笛卡尔空间轨迹规划及关节空间轨迹规划两类。笛卡尔坐标系复杂轨迹映射入关节轨迹空间十分困难，而在笛卡尔空间完成轨迹规划，将轨迹轮廓按精度分解为序列坐标点，逐一求解各点逆解，或实现关键点以外关节角插值是一种较简单的方法。

L-M方法求解精度高，速度快，但算法结果依赖给定的迭代初值，并且L-M方法是全局收敛算法，无法直接将迭代结果约束于关节角θi的可行域范围内，轨迹逆解结果易出现不可行的关节角。为解决上述问题，设计轨迹控制位置逆解算法流程图如图2所示。

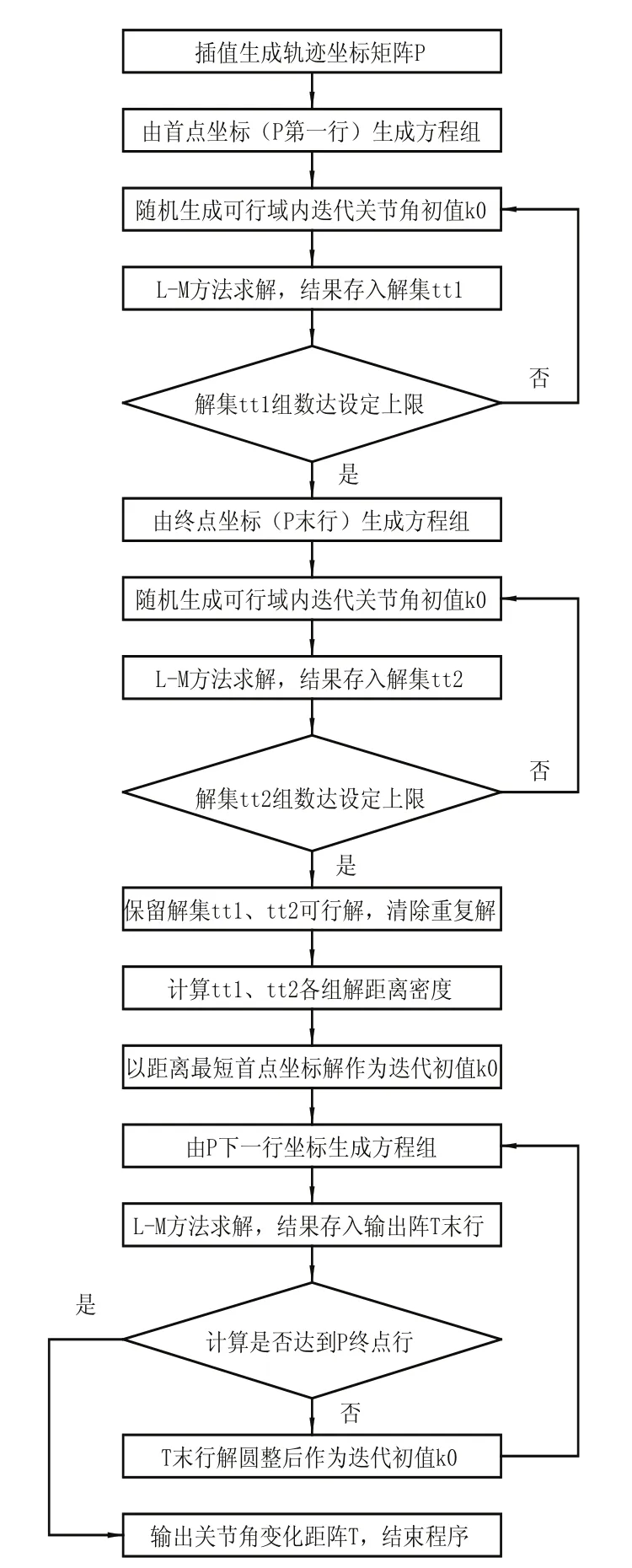
图2　轨迹规划位置逆解算法流程图

算法比较可行的轨迹首点逆解结果集tt1与终点逆解结果集tt2，取距离最短的两组解。轨迹中间序列点的迭代初值均使用前一点逆解结果的圆整值，即可控制逆解结果为系列连续变化的关节角矩阵。

将图2求得的关节角θ1、θ2、θ3代入式（5）～式（13），由机器人指定姿态的N、O、A向量构成姿态三元非线性方程组，采用类似算法可求变量θ4～θ6。

3　算法MATLAB仿真与分析

为验证算法有效性，利用MATLAB R2012b软件，编制轨迹控制逆逆解法程序，使用Intel Core i3 3.2GHz CPU、 4GB内存的计算机硬件环境仿真运行。

为直观比较预定轨迹坐标与算法逆解结果差异，设计轨迹控制目标为水平面正弦曲线如图3所示，星号点为逆解结果轨迹仿真结果，图中可见，设计轨迹与逆解结果轨迹各轴坐标误差低于10-7。逆解输出矩阵绘制关节角θ1～θ3变化曲线如图4所示。

图3　设计轨迹与逆解结果轨迹仿真对比

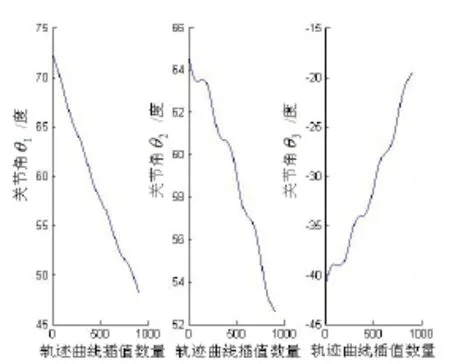
图4　逆解关节角θ1～θ3变化曲线

设定首点与终点逆解集上限为10次，求解图3轨迹900个坐标点，重复执行算法5次，设计轨迹与逆解结果轨迹三轴坐标最大误差为［3.009e-08，3.41e-13，7.751e-08］，中间插值点逆解经3次迭代终止，解算时间如表2

【】【】所示。与表2仿生智能算法相比，解算精度误差数量级同小于10-7务件下，L-M方法的迭代次数与耗时远优于微分进化逆解算法。

Fast inverse solution algorithm for trajectory planning of 6R robot based on L-M method

ZOU Li-mei， GUO Bo， QIAN Xue-yi

TP24

A

1009-0134（2016）10-0092-03

2016-06-27

福建省教育厅科技项目（JA14317）；福建省教育厅科技项目（JAT160513）

邹丽梅（1982 -），女，福建南平人，讲师，硕士，研究方向为机械电子工程。