Thermal behavior of hydrazinium 3,5-dinitramino-1,2,4-triazolate

LI Ji-zhen，ZHANG Guo-fang，FAN Xue-zhong，WANG Bo-zhou，ZHOU Cheng，FU Xiao-long，HUO Huan，HU Rong-zu

(1. Xi'an Modern Chemistry Research Institute, Xi'an　710065, China；2. Key Laboratory of Applied Surface and Colloid Chemistry, MOE/School of Chemistry & Chemical Engineering,Shaanxi Normal University, Xi'an　710062, China)



Thermal behavior of hydrazinium 3,5-dinitramino-1,2,4-triazolate

LI Ji-zhen1,2，ZHANG Guo-fang2，FAN Xue-zhong1，WANG Bo-zhou1，ZHOU Cheng1，FU Xiao-long1，HUO Huan1，HU Rong-zu1

(1. Xi'an Modern Chemistry Research Institute, Xi'an710065, China；2. Key Laboratory of Applied Surface and Colloid Chemistry, MOE/School of Chemistry & Chemical Engineering,Shaanxi Normal University, Xi'an710062, China)

hydrazinium 3,5-dinitramino-1,2,4-triazolate；energetic material；interaction；compatibility；thermal decomposition

0　Introduction

Compatibility of an energetic material refers to the change within a permissible range when the energetic material contacts with other materials by mixing or other processes[1-6]. In the practical applications of energetic materials, mixing of the energetic materials with explosives or components of propellants could give rise to some chemical interactions and thus lead to a potential danger to the propellants safety if the interactions are strong enough[1-3]. Therefore, compatibility is one of the important safety aspects related to the production and storage of energetic materials and studies on compatibility of energetic materials can decrease vulnerability of ammunition and weapons[1-3]. There are a few methods for evaluation of the compatibility of energetic materials[1-6], including Vacuum Stability Test (VST), Thermogravimetry (TG), Blush Pressure Method (BPM), and Differential Scanning Calorimetry (DSC), etc. To test different combinations of materials, DSC method with clear criteria is advisable[1-2]. In an investigation[3], it is shown that the results obtained with high-pressure DSC and TG/DTA measurements and obtained using vacuum stability tests were very similar for a same combination of materials.

Triazole-derived compounds[7-12]are energetic materials with low sensitivity and high energy. Hydrazinium 3,5-dinitramino-1,2,4-triazolate (HDNAT) is a new energetic triazole-derived ionic compound, which can be used as a main component in solid propellants and high explosives for its high energy. We experimentally find that nitrogen content of HDNAT is 50.8%, density 1.89 g/cm3, enthalpy of formation 216.37 kJ/kg, detonation velocity 9 400 m/s and detonation pressure 36.0 GPa. It is also found that the addition of HDNAT can obviously enhance burning rates of solid propellants by our experiments, the burning rate of the composite modified double-based propellant is increased by about 15% with addition of 5% HDNAT.

As a new energetic compound, thermal stability, interactions and compatibility of HDNAT with energetic materials in solid propellants or explosives are very important for HDNAT in its potential applications. Seldom, however, are investigations on these reported. Therefore in this work, thermal stability of HDNAT, interactions and compatibility of HDNAT with some energetic materials under the non-isothermal condition investigated by means of DSC technique, are reported.

1　Experiment

1.1Materials

HDNAT is prepared by Xi'an Modern Chemistry Research Institute according to the synthetic procedure described by Metelkina E L, et al[13], with purity of 99.83%. Cyclotetramethylenetetranitroamine (HMX), cyclotrimethylenetrinitramine (RDX), nitrocellulose (NC, 12.0%N), nitroglycerine (NG), 125/100-NC/NG mixture (NC+NG) N-nitrodihydroxyethylamine-dinitrate (DINA) 3,4-bisnitrofurazanfuroxan (DNTF) and aluminum powder (Al) are all industrially produced. Mixtures of HDNAT and energetic components are each prepared with 50% HDNAT.

The synthesis route of HDNAT is as follows.

1.2Experimental equipments and conditions

TG-DTG curves are obtained by using a TA 2950 thermogravimetric analyzer from TA Instruments (USA). The conditions for TG-DTG tests are as follows: sample mass, about 1.00 mg; heating rate (β), 5, 10, 15, 20 ℃/min; atmosphere, flowing rate of N2gas, 60 ml/min.

DSC measurements are made with a model Netzsch DSC 204 HP differential scanning calorimeter from Netzsch (Germany). The conditions for DSC measurements are as follows: sample mass, about 2.00 mg; heating rate, 10 ℃/min; atmosphere, nitrogen 0.1 MPa, flow rate 50 ml/min. The conditions for PDSC measurements are as follows: sample mass, about 2.00 mg; heating rate, 10 ℃/min; static nitrogen, 1.0 MPa.

The HDNAT, an employed energetic material of 2.00 mg or mixture of 50/50-HDNAT/each of the energetic materials of 1.00 mg/1.00 mg is sealed in an aluminum cell.

2　Results and Discussion

2.1Thermal decomposition behavior of HDNAT

The DSC curves at different pressures and TG-DTG curves at different heating rates of HDNAT are shown in Fig.1 and Fig.2, respectively.

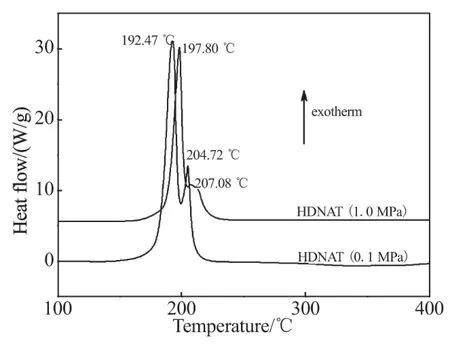
Fig.1　DSC curves of HDNAT at different pressures

The DSC curves of HDNAT show the decomposition processes in the temperature range of 160～230 ℃ with a main exothermic peak and a shoulder peak, where HDNAT decompose rapidly and form gas products. There are significant differences between the DSC curves of HDNAT at the pressures of 0.1 MPa and 1.0 MPa, at the latter pressure, the decomposition process of HDNAT is delayed because of the inhibition of gas products' escape by the pressure. With the change in pressure from 0.1 MPa to 1.0 MPa, the onset temperature changes from 180.72 ℃ to 186.64 ℃, the main exothermic peak temperature from 192.47 ℃ to 197.80 ℃, the shoulder peak temper-ature from 204.72 ℃ to 207.08 ℃, and the end temperature from 212.20 ℃ to 223.88 ℃.

Fig.2　TG-DTG curves of HDNAT at different heating rates

The TG-DTG curves of HDNAT (Fig.2) display a main peak with a shoulder in the DTG curves, corresponding to the two mass loss stages of HDNAT during its thermal decomposition. For the TG curve whenβ=10 ℃/min, the decomposition process begins at 177.24 ℃ and ends at 245.90 ℃, with the summit peak at 188.04 ℃ and the shoulder peak at 194.78 ℃, accompanied by 66.0% mass loss.

2.2Calculation of nonisothermal reaction kinetics

In order to obtain the kinetic parameters (the apparent activation energyEaand pre-exponential constantA) and the most probable kinetic model function, and explore the thermal decomposition mechanism of the major exothermic decomposition reaction of HDNAT, the DTG curves at heating rates of 5, 10, 15 and 20 ℃/min are dealt with mathematic means, and five integral methods [Eqs.(1)～(4) and (6)] and a differential method [Eq. (5)] listed in Table 1 are employed[14-16].

Table 1　Kinetic analysis methods

Where,αis the conversion degree of HDNAT decomposition;Tis the temperature (K) at time oft;T0is the temperature of the initial point at which the DTG curve deviates from the baseline;Tpis the peak temperature of DTG curve;Ris the gas constant;f(α) andG(α) are the differential model function and the integral model function, respectively; and the means ofEa,Aandβhave been mentioned earlier. Subscript s, data obtained byatava-esták's method; subscript k, data obtained by Kissiger's method; subscript o, data obtained by Ozawa's method. The data needed for the equations of the integral and differential methods,i,αi,β,Ti,Te(onset temperature),Tp,i=1, 2, 3, 4, are obtained from the DTG curves and summarized in Table 2.

Table 2　Data for decomposition processes of HDNAT at different heating rates from TG-DTG curves

The values ofEawere obtained by Ozawa's method [Eq.(6)] withαchanging from 0 to 1 as shown in Table 2. TheEa-αrelation is shown in Fig.3. It indicates that the activation energy of the decomposition processes changes greatly by diverse level with an increase in the conversion degree, except that for the range ofα=0.02～0.82, activation energy changes faintly, and it means that the decomposition mechanism of the process does not transfer in essence or the transference can be ignored. Therefore, it is feasible to research into the reaction mechanism and kinetics in the section ofα=0.02～0.82, according to the first mass loss stage, the main decomposition process of HDNAT in its TG curves.

Forty-one types of kinetic model functions in Ref.[11] and the original data (data points 2～50) tabulated in Table 2 are put into Eq. (1)～(8), respectively, for calculations. The values ofEa, lgA, linear correlation coefficient (r), and standard mean square deviation (Q) can be calculated with the linear least-squares method at various heating rates of 5, 10, 15 and 20 ℃/min, and

they are listed in Table 3. The most probable mechanism function is selected by the better values ofr, andQtaken from Ref.[11]. The results of satisfying the conditions mentioned above are also listed in Table 3.

Fig.3　Ea-α curve of HDNAT obtained by Ozawa's method

Methodβ/(℃/min)Ea/(kJ/mol)lg(A/s-1)rQOrdinary-integral5183.419.20.92990.299910191.820.10.93480.280615181.119.00.89370.448220185.619.50.94640.2308MacCallum-Tanner5183.819.30.93400.056510192.420.10.93840.052815181.619.00.89970.084520186.319.50.94960.0435Šatava-Šesták5180.218.90.93410.056510188.419.80.93850.052815178.318.70.89970.084520182.619.30.94970.0435Agrawal5183.419.20.92990.299910191.820.10.93480.280615181.119.00.89370.448220185.619.50.94640.2308Mean184.819.4——Kissiger185.719.30.99070.0182Ozawa183.9-0.99150.0034

The values ofEa, 184.8 kJ/mol, andA, 1019.4s-1, obtained from a single nonisothermal DTG curve are in approximately good agreement with the values calculated by Kissinger's method and Ozawa's method. Therefore, a conclusion can be drawn that the reaction mechanism of the main exothermal decomposition process of HDNAT is classified as nucleation and growth withn=2/5, and the mechanism function is No.12, the Avrami-Erufeev equation.

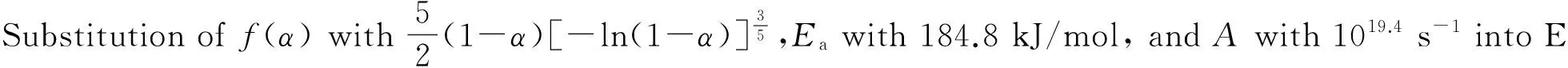
(7)

We can obtain the kinetic equation of the exothermal decomposition reaction as follows:

(8)

2.3Interactions of HDNAT with some energetic materials

Interactions of HDNAT with some energetic materials, such as HMX, RDX, NC, NG, etc., are studied in details by using DSC, and the typical DSC curves of the binary systems 1～8 are shown in Fig.4.

(c) HDNAT/NC　　　　　　　　　　　　　　　(d) HDNAT/NG

(e) HDNAT/NC+NG　　　　　　　　　　　　　　　(f) HDNAT/Al

(g) HDNAT/DINA　　　　　　　　　　　　　　　(h) HDNAT/DNTF

From Fig. 4 the following observations can be made.The DSC curve of HMX consists of two endothermic peaks and one exothermic peak. The first peak at 200.32 ℃ is due to the crystal transformation fromαtoδ, and the second endothermic peak at 280.30 ℃ is assigned to the phase change from solid to liquid. The exothermic peak at 281.89 ℃ is caused by the rapid decomposition reaction of HMX.

The endothermic peak in the DSC curve of RDX is caused by the phase change of RDX from solid to liquid. Similarly, the endothermic peaks in the DSC curves of DINA, HDNAT-DINA, DNTF and HDNAT-DNTF are caused by the phase changes of DINA and DNTF from solid to liquid.

The DSC curve of the HDNAT/HMX mixture shows two exothermic peaks at 198.22 ℃ (with a shoulder at 208.74 ℃) and 282.44 ℃, which are almost similar to the corresponding peaks of pure HDNAT (at 197.80 ℃ with a shoulder at 207.08 ℃) and HMX (281.89 ℃) under thermal decomposition. And the endothermic peak at 280.01 ℃ in the DSC curve of the HDNAT/HMX mixture has almost no difference with the corresponding peak of the phase change of pure HMX (280.30 ℃). Only the weak endothermic peak of the crystal transformation of HMX disappears because of the superposition with the sharp exothermic peaks of HDNAT in the DSC curve of the binary system. These observations manifest that there is nearly no interaction between HDNAT and HMX. And a similar result can be obtained for the binary system HDNAT/Al.

HDNAT, when mixed with RDX, decomposes rapidly in the temperature range of 186～197 ℃ centered at 193.88 ℃. The intermediate product of HDNAT decomposes with RDX, and a dull exothermic peak forms with peak temperature of 240.60 ℃. From the DSC curve of the HDNAT/RDX binary system, it can be observed that the endothermic peak of the phase change of RDX disappears because of the superposition with the shoulder peak of HDNAT, and the effect of RDX on HDNAT is more obvious than that of HDNAT on RDX.

There is little effect of NC, NG or (NC+NG) on HDNAT. The main exothermic peak and the shoulder peak of HDNAT have no significant change in their positions and shapes in the DSC curves of the binary systems of HDNAT-NC, HDNAT-NG and HDNAT-(NC+NG). However, the decomposition process of HDNAT influences those of NC, NG and (NC+NG) considerably, NC, NG and (NC+NG) decompose rapidly when blended with HDNAT in the temperature range of 170～240 ℃.

A striking interaction of DINA and HDNAT can be seen from the DSC curves of DINA, HDNAT and HDNAT/DINA. The decomposition of DINA is considerably accelerated by the addition of HDNAT with its exothermic peak moving from 197.80 ℃ to 183.78 ℃. Similarly, HDNAT shows its exothermic peak and shoulder peak at 183.78 ℃ (197.80 ℃ in pure HDNAT) and 204.73 ℃ (207.08 ℃ in pure HDNAT), respectively, in the DSC curve of HDNAT/DINA.

The DSC curve of HDNAT/DNTF shows an evident interaction between HDNAT and DNTF, too. A main exothermic peak and a small shoulder peak at 187.02 ℃ and 222.60 ℃, respectively, are shown in the DSC curve of the HDNAT/DNTF binary system.

2.4Compatibility of HDNAT with some energetic materials

The compatibility of HDNAT with the energetic materials mentioned above is evaluated with the data of DSC curves above. The maximum exothermic peak temperatures of the energetic materials and the 50/50-HDNAT/energetic material binary systems are shown in Table 4.Where mixture system, 50/50-HDNAT/energetic component binary system; Single system, the component with its exothermic peak temperature smaller than another one in a two-component system;TP1, the maximum exothermic peak temperature of single system;TP2, the maximum exothermic peak temperature of mixture system; ΔTP=TP1-TP2.The evaluation standard of compatibility for explosives and contacted materials[1-2]are listed in Table 5.

From both Table 4 and Table 5, the following observations can be made.

Decomposition process of HDNAT is delayed by the addition of HMX and Al, the maximum exothermic peak temperature differences (ΔTp) between HDNAT and HDNAT-HMX or HDNAT-Al are -0.42 and -0.54 ℃, respectively. From the evaluation standard of compatibility in Table 5, it is concluded that the binary systems HDNAT-HMX or HDNAT-Al have good compatibility.

The DSC curve of the binary system HDNAT-NC shows that there is only a little effect on the decomposition processes of HDNAT or NC by mixing HDNAT and NC, and the binary systems of HDNAT-NG and HDNAT-(NC+NG) are in the same way. The values of ΔTpare 0.48 ℃ between HDNAT and HDNAT-NC, 1.50 ℃ between HDNAT and HDNAT-NG, and 1.78 ℃ between HDNAT and HDNAT-(NC+NG), which indicate good compatibility between HDNAT and NC, NG or (NC+NG), too.

Table 4　Data of the energetic materials and the 50/50-HDNAT/energetic material mixtures obtained by DSC

Table 5　Evaluation standard of compatibility for explosives and contacted materials

The value of ΔTpbetween HDNAT and HDNAT-RDX is 3.92 ℃, which displays that the decomposition reaction of the mixture is easy to take place and the mixture has fair compatibility.

The values of ΔTpbetween DINA and HDNAT-DINA, DNTF and HDNAT-DNTF are 14.02 and 10.78 ℃, respectively, showing an increase in the rates of the decomposition reactions and a poor compatibility of the mixtures.

The compatibility of the binary systems of HDNAT/energetic materials decreases in the order 6>1>3>4>5>2>8>7, and the relative thermal stability of the binary systems of HDNAT/energetic materials decreases in the same way.

3　Conclusions

There is obvious interactions between HDNAT and DINA or DNTF, a slight interaction between HDNAT and RDX, while little interactions between HDNAT and HMX, NC, NG, (NC+NG) or Al.

The HDNAT-HMX, HDNAT-NC, HDNAT-NG, HDNAT-(NC+NG) and HDNAT-Al binary mixtures have good compatibility, and the HDNAT-RDX binary mixture has fair compatibility, and the HDNAT-DINA and HDNAT-DNTF binary systems have poor compatibility, however.

[1]Beach N E, Canfield V K. Compatibility of explosives with polymers (III) [J]. Plastic. Rep., 1971, 40:73-76.

[2]Beach, N E, Canfield V K. Compatibility of explosives with polymers (II) [R]. AD 721004, Springfield: NTIS, 1971.

[3]W P C de Klerk, M A Schrader, A C van der Steen. Compatibility testing of energetic materials, which technique [J]. J. Therm. Anal. Cal., 1999, 56(3):1123-1131.

[4]Yan Q L, Li X J, Zhang L Y, et al. Compatibility study of trans-1,4,5,8-tetranitro-1,4,5,8- tetraazadecalin (TNAD) with some energetic components and inert materials [J]. J. Hazard Mater., 2007, 160(2-3):529-534.

[5]Liao L Q, Wei H Jian, Li J Z, et al. Compatibility of PNIMMO with some energetic materials [J]. J. Therm. Anal. Cal., 2012, 109(3):1571-1576.

[6]Li J Z, Fan X Z, Fan X P, et al. Compatibility study of 1,3,3-tinitroaztidine with some energetic components and inert materials [J]. J. Therm. Anal. Cal., 2006, 85(3):779-784.

[7]Wang Bozhou, Li Jizhen, Huo Huan, et al. Synthesis, characterization and thermal behaviors of 4-Amino-5-nitro-1,2,3-triazole (ANTZ) and its derivatives [J]. Chin. J. Chem., 2010, 28(5): 781-784.

[8]Lsimpsom, R P, Pagoria A R, Mitchaland C L. Synthesis, properties and performance of the high explosive ANTA[J]. Prop. Exp. Pyro., 1994, 19(4):174-179.

[9]Kien L, Ott Y, Donald G.Production of the ammonium salt of 3,5-dinitro-l,2,4-tiazole by solvent extraction [P], USP 4236014, 1980.

[10]Xiong C L, Jia S Y, Wang X J, et al. Synthesis and extraction of anunonium salt of 3,5-dinitro-1,2,4-triazole [J]. Fine Chemical Intermediates, 2008, 38(2): 64-66 (in Chinese).

[11]Jia S Y, Wang X J, Wang B Z, et al. Synthesis and crystal structure of 3,3'-dinitro-5,5'-azo-1H-1,2,4-triazole (DNAT) [J]. Chin. J. Exp. Prop., 2009, 32(1): 25-28 (in Chinese).

[12]Darren L N, Michael A H, Herbert H H. Synthesis and explosive properties of 3,3'-dinitro-5,5'-azo-1H-1,2,4-triazole [J]. Ener. Mater., 2003, 21(1): 57-62.

[13]Metelkina E L. 2-Nitroguanidine derivatives: V. synthesis and structure of 3,5-Bis(nitroamino)-1,2,4-triazole salts. acid-base properties of 3,5-bis(nitroamino)-1,2,4-triazole [J]. Russian J. Org. Chem., 2004, 40(4): 543-550.

[14]Hu R Z, Shi Q Z. Thermal analysis kinetics [M]. Beijing: Science Press, 2001 (in Chinese).

[15]Wu X M, Liu J H, Li W, et al. Thermal decomposition kinetics of complexes of rare earths (RE=Nd, Sm) with amino acid RE(Val)Cl3·6H2O [J]. Acta Phys. Chim. Sin., 2006, 22(8): 942-946.

[16]Hu R Z, Chen S P, Gao S L, et al. Thermal decomposition kinetics of the Pb0.25Ba0.75(TNR)center dot H2O complex [J]. J. Hazard. Mater., 2005, 117(2-3): 103-110.

(编辑：薛永利)

3,5-(硝氨基)-1,2,4-三唑肼盐的热行为研究

李吉祯1,2，张国防2，樊学忠1，王伯周1，周诚1，付小龙1，霍欢1，胡荣祖1

(1. 西安近代化学研究所，西安710065；2. 应用表面和胶体化学教育部重点实验室，陕西师范大学化学化工学院，西安710062)

3,5-(硝氨基)-1,2,4-三唑肼盐；含能材料；相互作用；相容性;热分解

V512Document Code：AArticle ID：1006-2793(2016)04-0529-09

10.7673/j.issn.1006-2793.2016.04.015

Receivied date：2016-03-01；Revised date：2016-04-21。

Fundation project：Supported by the National Sciense Fundation of China(21401124);China Postdoctional Science Fundation(2014M560745)。

Biography：LI Ji-zhen(1980—)，mail，associate professor,speciality:Solid rocket propellent.E-mail:JizhenLi@126.com