机动目标多传感器组网空间配准方法

方　峰，蔡远利

(西安交通大学 电子与信息工程学院，西安　710049)



机动目标多传感器组网空间配准方法

方峰，蔡远利

(西安交通大学 电子与信息工程学院，西安710049)

针对存在传感器偏差的多传感器组网系统跟踪机动目标的问题，把目标状态与传感器偏差进行解耦估计，提出了一种基于交互多模型的两阶段扩展Kalman滤波(IMM-TSEKF)算法。由于传感器观测方程的非线性，文中采用了两阶段扩展Kalman滤波器(TSEKF)，针对机动目标，把IMM算法与TSEKF算法相结合用于目标跟踪与空间配准。此外还对算法的时间复杂度进行了分析，并以螺旋机动战术弹道导弹为目标进行组网空间配准与目标跟踪。仿真结果表明，相比于常规的基于交互多模型的增广Kalman滤波(IMM-ASEKF)算法，该文算法在估计性能相当的情况下，减小了计算的复杂度，提高了计算效率，更易于工程实现。

两阶段Kalman滤波；交互多模型；目标跟踪；空间配准

0　引言

在目标跟踪系统中，多传感器组网系统利用数据融合技术可增强跟踪系统的性能。但在实际应用中，组网系统的传感器均可能存在系统偏差和随机干扰，在进行数据融合之前必须对传感器进行空间配准[1-2]。

空间配准又称为传感器配准，就是借助于多传感器关于共同目标的测量对传感器的偏差进行估计和补偿。针对空间配准，常用的方法有离线配准法和在线配准法。离线配准法主要包括最小二乘法[3]、精确极大似然法[4]等，但是这类方法的实时性不高。而在线配准法能够实时进行空间配准，它主要有：增广Kalman滤波算法，如增广扩展Kalman滤波(ASEKF)算法[5]、增广UKF算法[6]等；基于高斯均值移动的配准算法[7]，基于EM准则的配准算法[8-9]，基于熵函数法的配准算法[10]等。由于增广Kalman滤波算法的可实现性强、估计精度高，它在实际应用中最为广泛。然而由于增广Kalman滤波算法把传感器偏差增广到了系统状态中，当传感器偏差个数较多时，会引起维数灾难，且在某些病态情况下会出现数值计算问题。基于此，由Berand Friedland提出的两阶段卡尔曼滤波器[11-14](TSKF)能够很好地解决状态增广带来的计算问题。TSKF将状态和偏差进行解耦估计，减小了计算的复杂度，且稳定性更好，更易于工程实现。此外，在进行空间配准时，上述文献大多都只考虑了目标做弱机动的情况。然而，当目标做强机动飞行时，就需要进一步考虑滤波算法跟踪机动目标的能力。

由于交互多模型(IMM)算法[15]对机动目标有很好的跟踪能力，故本文将IMM算法与两阶段扩展Kalman滤波(TSEKF)算法相结合，提出了IMM-TSEKF算法用于机动目标跟踪和传感器偏差估计。IMM-TSEKF将系统状态和传感器偏差进行解耦估计，避免了由状态增广引起的维数灾难。针对战术弹道导弹(TBM)在再入段进行螺旋机动的情况进行目标跟踪与空间配准，仿真结果表明，本文算法能够很好地跟踪螺旋机动TBM，且相比于常规的交互多模型增广扩展Kalman滤波(IMM-ASEKF)算法，本文算法在估计精度相当的同时，降低了计算的时间复杂度，算法的稳定性更好，更易于工程实现。

1　两阶段扩展Kalman滤波器

1.1问题描述

考虑多传感器组网系统，假设有L个传感器，且认为各传感器之间同步工作。系统采用集中式融合估计对目标进行跟踪，目标的状态方程和传感器的观测方程可表示如下：

(1)

(2)

式中Xk为目标状态向量；Fk为状态转移阵；h(·)为非线性函数；Zk+1为观测向量，Zk+1=[z1，k+1，z2，k+1，…，zL，k+1]T，其中zi，k+1表示第i个传感器的观测向量；b为传感器的固定偏差，b=[b1，b2，…，bL]T，其中bi表示第i个传感器的偏差向量；ωk为过程噪声；vk为观测噪声。

过程噪声ωk和观测噪声vk相互独立，且都是零均值的高斯白噪声，协方差矩阵分别为Qk和Rk。ωk、vk与状态初值X0相互独立。

1.2TSEKF算法

由于TSKF只适用于线性系统，为了将其推广到非线性系统，本文引入扩展Kalman滤波的思想，从而得到两阶段扩展Kalman滤波器(TSEKF)。TSEKF的基本思想是先将系统线性化，即将非线性系统在状态预测值和偏差预测值处进行泰勒级数展开，保留线性主导项；然后对线性化后得到的系统运用TSKF算法进行滤波。

1.2.1系统线性化

(3)

其中

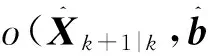
将式(3)取一阶线性项并进行整理，可得

(4)

其中

通过上述变化，式(4)就是线性化后的观测方程。

1.2.2TSKF

将线性化后得到的式(1)和式(4)所表征的线性系统，运用TSKF算法进行滤波，具体步骤如下：

(1)“无偏差滤波器”

(5)

(6)

(7)

(8)

(9)

(2)偏差滤波器

(10)

Sk=HkUk+Ck

(11)

(12)

(13)

(14)

(15)

(16)

(17)

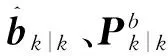
(3)系统状态真实估计值

(18)

(19)

(20)

(21)

2　IMM-TSEKF

本节将TSEKF算法与IMM算法相结合，推导得到了IMM-TSEKF算法。IMM-TSEKF算法包括输入初值交互、TSEKF滤波器、模型概率估计器和估计混合器。

图1　IMM-TSEKF算法流程图

IMM-TSEKF算法从k-1时刻到k时刻的递推步骤如下：

(1)输入初值交互

IMM-TSEKF的输入初值交互包括“无偏差滤波器”的输入初值交互和偏差滤波器的输入初值交互这两部分。

首先，进行“无偏差滤波器”的输入初值交互。由IMM算法的输入交互计算式，可得

(22)

(23)

又由TSEKF中的式(20)、式(21)可知模型j的状态估计值和协方差矩阵分别为

(24)

(25)

如式(24)和式(25)所示，TSEKF将无偏差状态估计与偏差估计进行耦合得到真正的系统状态估计，故IMM-TSEKF在进行状态的输入初值交互时，也按照这种耦合形式进行计算。由此，模型j的状态输入初值交互定义为

(26)

(27)

将式(24)、式(25)代入式(22)、式(23)中，并与式(26)、式(27)对比，可得模型j的“无偏差滤波器”的输入交互初值和相应的协方差阵：

(28)

(29)

然后，进行偏差滤波器的输入初值交互。模型j的偏差滤波器的输入交互初值和相应的协方差矩阵为

(30)

(31)

(2)TSEKF滤波

(3)模型概率更新

(32)

将式(11)和式(18)代入可得

(33)

将式(33)与式(15)对比发现，模型j的新息就是偏差滤波器的新息。

(34)

由此，可得似然函数为

(35)

模型概率更新为

(36)

其中

(4)组合滤波输出

(37)

其中

(38)

其中

(39)

(40)

3　算法的时间复杂度分析

算法复杂度是一种衡量算法有效性的概念，可以分为算法的空间复杂度和算法的时间复杂度。在实际中，最广泛使用的算法复杂度概念一般是指算法的时间复杂度。本文把执行算法过程中所需要的基本运算次数表示为时间复杂度[13]，并且假定所需的基本运算次数为加法和乘法的运算次数之和。

下面对IMM-TSEKF算法与常规的IMM-ASEKF算法进行时间复杂度分析。常规的IMM-ASEKF算法是将传感器偏差增广到系统状态中去，然后再应用IMM-EKF进行估计。由于这2种方法在计算模型交互概率，似然函数以及模型概率时所需的基本运算次数相同，故在接下来的时间复杂度分析中不再予以考虑。借鉴文献[13]，且近似地认为2个n维方阵相乘所需的运算次数为2n3，对算法时间复杂度进行定量计算。

首先，计算交互多模型标准Kalman滤波算法的时间复杂度，主要分3个阶段。

(41)

(42)

(43)

OPT(n，m，p，N)=(2n2p+4nmp+np+mp)N

(44)

式(41)～式(44)中的n、m、p、N分别表示状态的维数、观测数据的维数、传感器偏差个数及模型个数。

由以上分析可得IMM-ASEKF的时间复杂度：

(45)

本文算法IMM-TSEKF的时间复杂度为

(46)

比较式(45)和式(46)可看出，IMM-TSEKF与IMM-ASEKF相比，节省的运算次数为

(47)

4　仿真实验

以多无源传感器组网跟踪系统为例进行仿真。无源传感器只能得到目标的方位角和俯仰角的观测值，且存在固定的传感器系统偏差。无源传感器的观测方程为

(48)

式中φi、θi分别表示第i个传感器的方位角和俯仰角的量测值；Δφi、Δθi为相应的传感器固定偏差；Si=(xsi，ysi，zsi)为第i个传感器所在的位置；ν1i、ν2i为观测噪声。

设三维空间内有3个无源传感器，分别静止地位于S1=(0 km，0 km，50 km)，S2=(50 km，0 km，0 km)，S3=(0 km，0 km，-50 km)这3处。3个传感器的偏差分别为Δφ1=Δθ1=2°， Δφ2=Δθ2=2°，Δφ3=Δθ3=3°。传感器的观测噪声是零均值的高斯白噪声，方差为(0.1°)2。3个无源传感器同步工作，采样周期为T=0.4 s。

假设跟踪目标为战术弹道导弹，TBM在再入过程中做螺旋机动。本文按照TBM的动力学方程、运动学方程以及姿态运动方程等产生机动螺旋弹道，详细的TBM再入机动螺旋弹道建模见参考文献[16]。TBM螺旋弹道数据是在地面坐标系下生成的。TBM螺旋弹道初始参数设置如下：

(xT0=0 km，yT0=32 km，zT0=36 km)，VT0=1 km/s，弹体初始自旋角γT=0°，弹体初始自旋角速度ω1xT=0(°)/s，速度偏航角φT0=0°，速度倾角θT0=175°，弹道系数B=5 000 kg/m2，滚动阻尼系数b=0.008 m2/kg，滚动干扰力矩系数c=2.3×10-6m/kg。

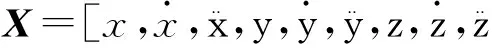
图2　TBM真实弹道与估计弹道的对比

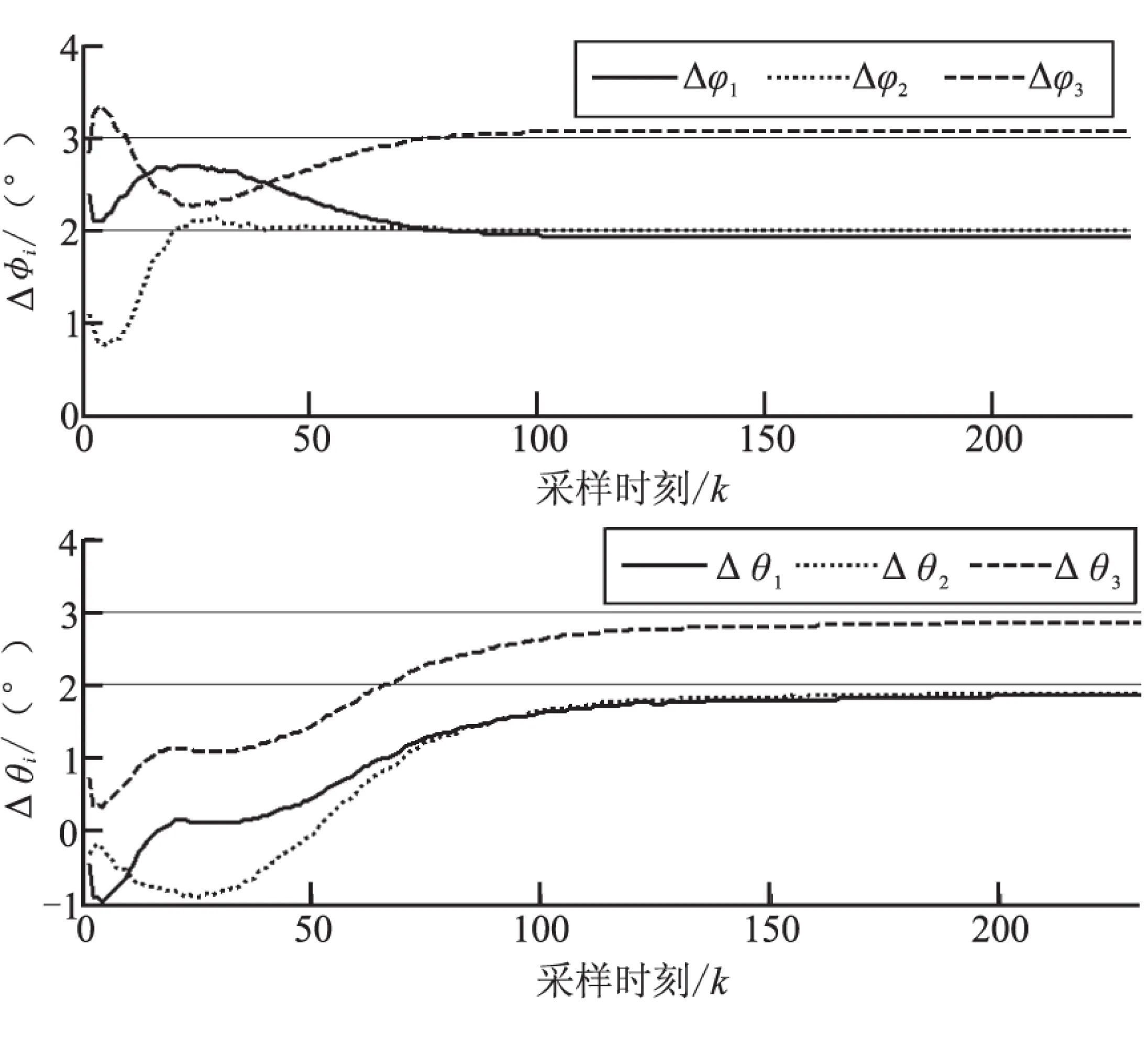
图3　各传感器的偏差估计

图4　TBM位置估计的均方根误差

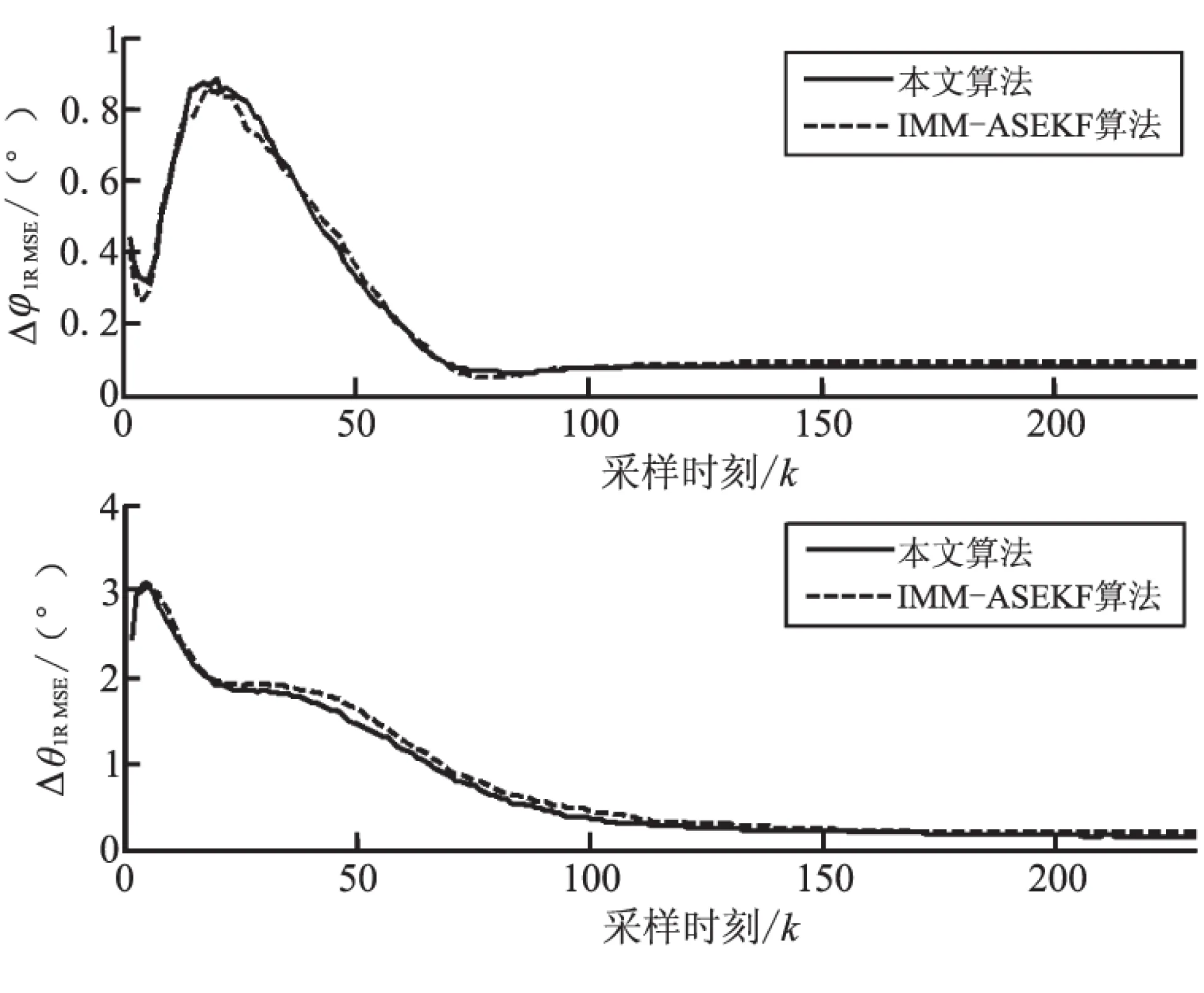
(a)传感器1

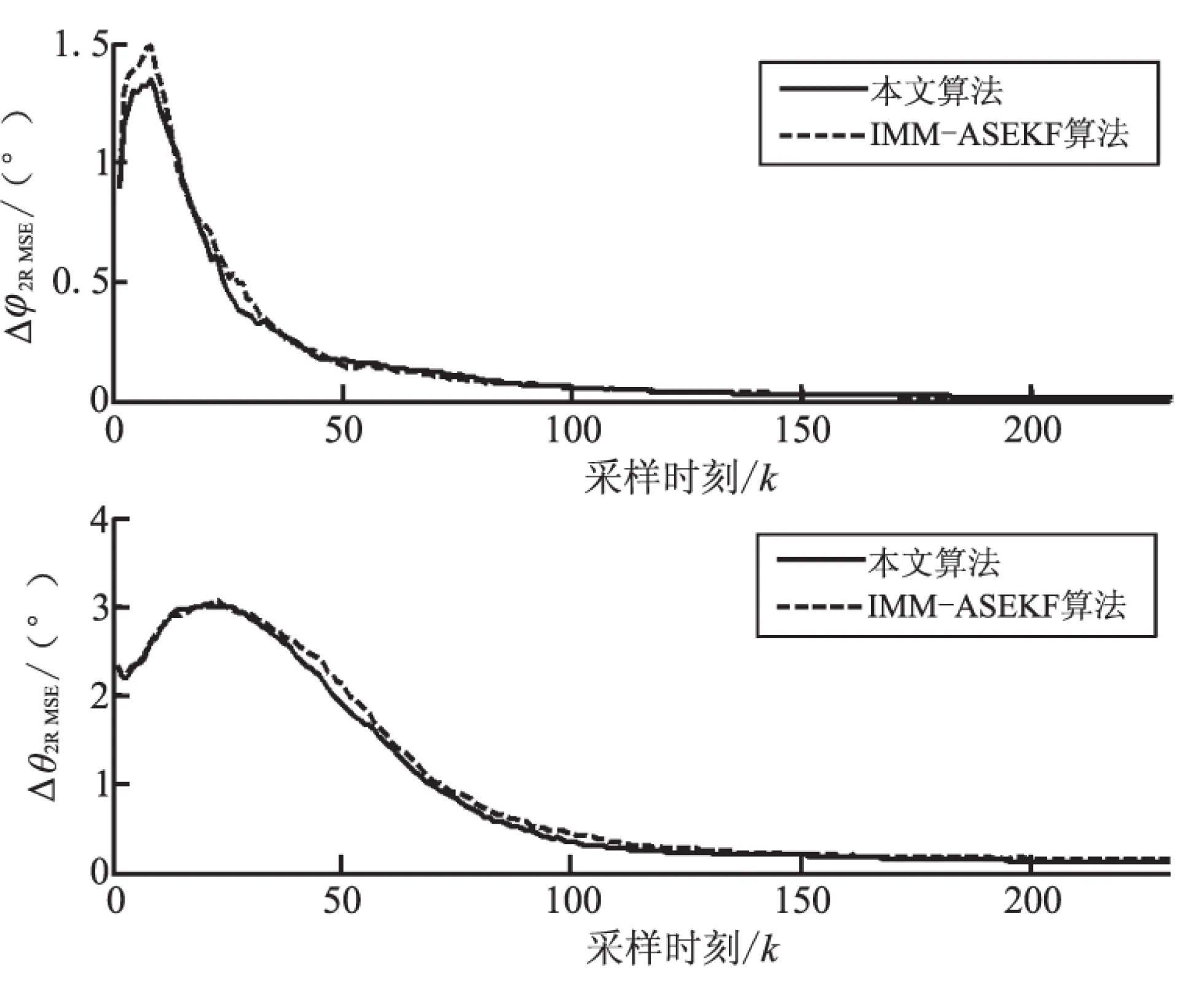
(b)传感器2

(c)传感器3

利用IMM-TSEKF进行50次蒙特卡洛仿真，并将其与IMM-ASEKF进行比较，得到仿真结果如图2～图5所示。从图2可见，利用本文算法进行空间配准以后，系统能够很好地跟踪做螺旋机动的TBM。由图3可见，本文算法可很好地对传感器偏差进行估计。图4、图5为本文算法与常规的IMM-ASEKF算法的动态性能比较图，可见本文算法与IMM-ASEKF算法估计效果相当。

表1给出了采样时刻k=240时的2种算法的性能指标。对比可看出，2种算法的状态估计和偏差估计的均方根误差基本相等。另外，由表1的运算次数对比可看出，当进行一步递推滤波时，本文算法可以节约32 633次运算操作。同时，利用第四节的算法时间复杂度进行分析，当n=9，m=6，p=6，N=2时，由式(47)计算可得，进行一步递推滤波时，本文算法可以节省34 404次运算操作，与实验结果相近(只有5%的相对误差)。

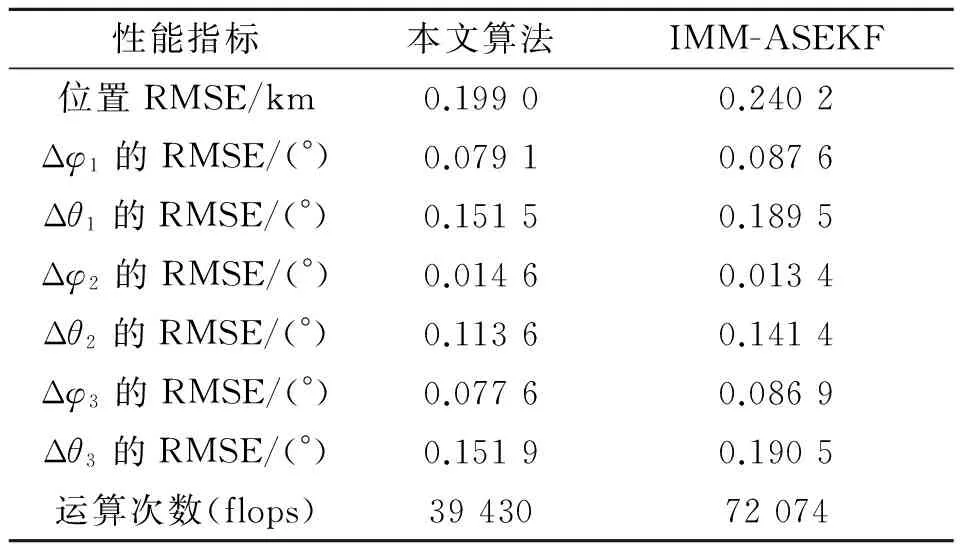
表1　2种算法的性能比较

5　结论

(1)针对机动目标多传感器组网跟踪与空间配准的问题，提出了IMM-TSEKF算法，该算法将目标状态与传感器偏差进行解耦估计，避免了状态增广带来的计算复杂及数值计算精度低的问题。另外还对IMM-TSEKF算法与IMM-ASEKF算法进行了时间复杂度的定量分析。

(2)以螺旋机动战术弹道导弹为机动目标进行仿真，结果表明本文算法能很好地完成空间配准与机动目标跟踪，且相较于IMM-ASEKF算法，本文算法在估计精度相当的情况下，减小了计算的时间复杂度，提高了计算效率，更适用于工程应用。

[1]韩崇昭,朱洪艳,段战胜.多源信息融合[M].北京: 清华大学出版社,2006.

[2]王成飞,王航宇,石章松.基于两级扩展Kalman滤波的海上多平台误差配准算法[J].系统工程与电子技术,2011,33(4):851-855.

[3]Leung H,Blanchette.M.A least squares fusion of multiple radar data[C]//Proceedings of RADAR,Paris,1994: 364-369.

[4]Zhou Y F,Leung H.An exact maximum likelihood registration algorithm for data fusion[J].IEEE Trans on Signal Processing.1997,45(6): 1560-1572.

[5]NABAA N,BISHOP R H.Solution to a multisensor tracking problem with sensor registration errors [J].IEEE Trans on Aerospace and Electronic Systems,1999,35(1):354-363.

[6]胡洪涛,敬忠良,胡士强.一种基于Unscented卡尔曼滤波的多平台多传感器配准算法[J].上海交通大学学报,2005,39(9):1518-1521.

[7]Qi Yong-qing,Jing Zhong-liang,Hu Shi-qiang ,et al.A new method for dynamic bias estimation: Gaussian mean shift registration [J].Optical Engineering,2008,47(2):401-408.

[8]Zia A,Kirubarajan T,et al.An EM algorithm for nonlinear state estimation with model uncertainties [J].IEEE Trans on Signal Processing,2008,56(3):921-936.

[9]Li Zhen-hua,Chen Si-yue,Leung H.Joint data association,registration,and fusion using EM-EKF[J].IEEE Trans on Aerospace and Electronic Systems,2010,46(2): 496-507.

[10]郭军军,元向辉,韩崇昭.采用熵函数法的多传感器空间配准算法的研究[J].西安交通大学学报,2014,48,(11):128-134.

[11]Friedland B.Treatment of bias in recursive filtering[J].IEEE Trans on Automatic Control,1969,14(4): 359-367.

[12]Hsieh C S,Chen F C.Optimal solution of the two-stage Kalman estimator [J].IEEE Trans on Automatic Control,1999,44(1): 194-199.

[13]Karsaz A,Khaloozadeh H,Darbandi M.Performance comparison of the two-stage Kalman filtering techniques for target tracking[C]//Proceeding of International Symposium on Systems and Control in Aeronautics and Astronautics.2010:942-947.

[14]Kim K H,Lee J G,Park C G.Adaptive two-stage extended Kalman filter for a fault-tolerant INS-GPS loosely coupled system[J].IEEE Trans on Aerospace and Electronic Systems,2009,45(1):125-137.

[15]Foo P H,Ng G W.Combining the interacting multiple model method with particle filters for manoeuvring target tracking[J].IET Radar Sonar Navig.,2011,5(3):234-255.

[16]熊柯,郭振云.反导导弹末制导与控制[D].国防科技大学,2006.

[17]王伟平,徐毓,王杰.基于改进“当前”统计模型的的非线性机动目标跟踪算法[J].控制理论与应用,2011,28(12):1723-1728

(编辑：吕耀辉)

Multi-sensor space registration for maneuvering target tracking

FANG Feng，CAI Yuan-li

(School of the Electronic and Information Engineering，Xi’an Jiaotong University，Xi’an710049，China)

For the maneuvering target tracking problem with multi-sensor bias,a two-stage extended Kalman filter based on interacting multiple model(IMM-TSEKF)algorithm was proposed in this paper.The algorithm decoupled the augmented filter into two parallel reduced-order filter-one for state estimation and another for bias estimation.Firstly,the two-stage extended Kalman filter for the case of nonlinear system was employed.Secondly,the IMM-TSEKF algorithm for the purpose of maneuvering target tracking and space registration was adopted.Besides,the time complexity of the algorithm was analyzed.Lastly,the tactical ballistic missile using spiral maneuver was utilized as maneuvering target for space registration and target tracking.Simulation results show that the presented algorithm has higher computation efficiency and similar performance compared with traditional augmented state Kalman filter.

two-stage Kalman filter；interacting multiple model；maneuvering target tracking；space registration

2015-05-06；

2015-08-20。

国家自然科学基金(61202128)；宇航动力学国家重点实验室开放基金(2011ADL-JD0202)。

方峰(1991—)，男，博士生，研究方向为信息融合、飞行器制导与控制。E-mail：arrowfang @stu.xjtu.edu.cn

蔡远利(1963—)，男，博士生导师，研究方向包括复杂系统建模与仿真、飞行器制导与控制、飞行动力学等。

V443；TN953

A

1006-2793(2016)04-0574-06

10.7673/j.issn.1006-2793.2016.04.023