考虑温度效应的多层粘弹性矩形板的动力响应

张震东，马大为，任　杰，何　强，高　原，王　旭

(1.南京理工大学 机械工程学院，南京　210094；2.第二炮兵装备研究院，北京　100094)



考虑温度效应的多层粘弹性矩形板的动力响应

张震东1，马大为1，任杰1，何强1，高原2，王旭2

(1.南京理工大学 机械工程学院，南京210094；2.第二炮兵装备研究院，北京100094)

根据热粘弹性本构模型及时-温等效原理，结合Kirchhoff薄板理论，推导了考虑温度效应的多层粘弹性板的板的运动微分方程。采用级数分解和Laplace积分变换相结合的方法，给出了圆形均布动载荷及温度载荷联合作用下多层板的挠度解析表达式。采用具有较高精度的BURBIN F方法求解Laplace积分逆变换，在MATLAB软件中编写计算程序，以2层薄板为例分析了初始温度、表面变温速率对板动力响应的影响。结果表明，初始温度越高，板的挠度越大，随着时间的增长，横向位移有所增加；变温速率越大，挠度变化幅度越大；相同幅度的变温速率下，升温对挠度的影响大于降温。

热粘弹性本构；温度效应；薄板理论；动力响应；Laplace积分逆变换

0　引言

新型复合材料板由于具有密度低、力学性能好等优点，近年来被广泛用于航空航天领域，而这些材料一般都表现出一定的蠕变和应力松弛特性，其力学行为与粘弹性材料相近。因此，国内外学者采用粘弹性理论，对这类板的动态特性进行了较多研究。

国内方面，祝彦知等[1]分析了粘弹性地基上粘弹性板的自由振动问题，得到了3种粘弹性模型矩形薄板的固有频率解析解。彭凡等[2]基于Boltzman积分型本构关系，研究了线粘弹性薄板在考虑几何线性与非线性时的动力稳定特性问题。傅衣铭等[3-4]采用Von Karman板理论和复合材料单层板的损伤模型，分析了考虑温度效应时板的动力响应，但假设板为均匀变温，未涉及热传导问题。王燕楠等[5-7]则建立了含热传导效应的粘弹性板耦合非线性动力分析模型，并发展了相应的数值分析方法。国外学者也对粘弹性板问题进行了相关研究，Igor Bock[8]采用Von Karman板理论对粘弹性板的大变形问题进行了深入研究。Kim Tae Woo等[9]探讨了粘弹性层合板的非线性振动问题。Assie A E等[10]基于Mindlin-Reissner薄板理论，对瞬态载荷下各向异性粘弹性复合材料板的动力响应进行了分析，并通过有限元方法得到了数值解。Saeed Masoumi等[11]采用广义微分求积法，多角度分析了粘弹性复合材料板的弯曲问题。Zhou Yin-feng等[12]则应用广义微分求积法，求解了变厚度粘弹性板在各种边界条件下的自由振动频率。Raffaele Barretta等[13]基于Kirchhoff薄板理论，给出了各向同性粘弹性功能梯度板的精确解。Dai Hong-liang等[14]在经典的薄板理论以及Von Karman非线性应变-位移关系的基础上，分析了复合材料窄长板的热粘弹性动力响应。

国外学者虽然采用多种不同方法研究了粘弹性板的动力响应问题，但很少考虑温度的作用，值得注意的是国内一些研究中包含了热效应，多数学者只关注了热应力对单层板运动状态的影响，并未分析由温度引起的材料性能的变化对板动力响应改变。

本文基于热粘弹性本构模型，结合时-温等效原理，并考虑温度与材料力学性能的相关性，采用Kirchhoff薄板理论，以2层粘弹性板为例，分析了板的动力响应问题，得到了一些有意义的结论。

1　热粘弹性本构有温度效应

1.1热粘弹性本构模型

二维状态下，变温粘弹性本构为[4,14]

(1)

式中E(t)为松弛模量；μ为泊松比；α为线膨胀系数；T(t)为平面温度场；⊗为Stieltjes卷积运算符号。

对式(1)进行Laplace变换，并利用Stieltjes卷积的性质，可得到：

(2)

1.2变温条件下的应力松弛模量

由M个Maxwell体并联组成的广义粘弹性模型，可解释复杂的应力松弛现象，参考温度下的松弛模量可表示为

(3)

式中TR为参考温度；EK(TR)为第K个Maxwell单元的弹性模量；τK=ηK/EK为松弛时间；ηK(T)为第K个Maxwell单元的粘性常数。

根据时-温等效原理，某一温度条件下的应力松弛过程，可用不同温度条件下的模量-时间曲线拟合而得。时温等效可表示为

(4)

式中λT为位移因子。

可用式(5)确定位移因子λT：

(5)

式中δH为材料活化能；R为摩尔气体常数。

由时-温等效原理得到：

(6)

1.3温度场模型

本文温度场沿x、y方向均匀分布，于是可假设变温速率为

式中ΔT0为多层板上表面变温速率；H为板总厚。

若板的初始温度为Tini，则板内任一点的温度为

(7)

将式(7)代入式(5)，则位移因子可写成：

(8)

2　多层板的内力平衡方程

圆形均布载荷作用下多层矩形板模型如图1所示，由于板的厚宽比很小，故认为多层板在动载荷作用下的变形满足Kirchhoff薄板假设。

根据薄板理论假定，可得应变分量为

(9)

从多层板中取底边为dx、dy、高为H的微小六面体为研究对象，分别对x轴、y轴取矩，由力矩平衡方程，以及z方向的力平衡方程得到：

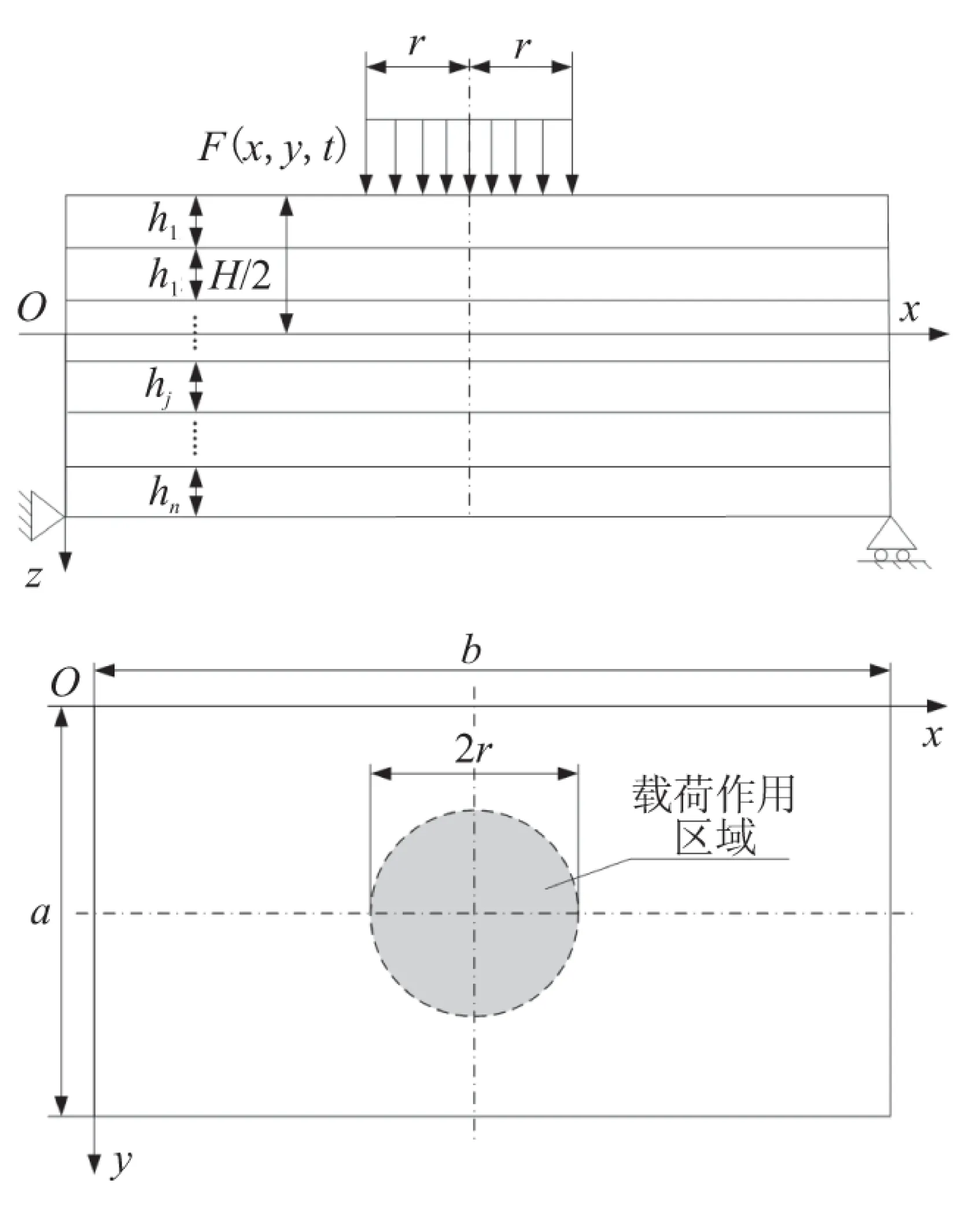
图1　多层矩形板模型

其中，F(x,y,t)为外载荷；Qx(x,y,t)、Qy(x,y,t)为剪力，且有

式中ρn为第n层板的密度；hn为第n层板板厚；N为板层数。

分别对式(10)中的第1式、第2式求x、y偏导，并代入第3式，可得到z方向的力平衡方程为

(11)

将式(9)进行拉氏变换，并代入式(2)，然后代入Laplace变换后的式(11)，同时根据温度x，y方向均匀分布的假定，对ΔT(t)求偏导后，相应的偏导数为0，于是可得到：

其中

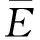
3　平衡方程求解

3.1边界条件及载荷模型

假设多层板四边简支，则边界条件可表示为

(13)

圆形均布动载荷表达式如下：

(14)

式中f(t)为载荷平均集度，本文取承载板上载荷平均集度变化规律为f(t)=0.1×sin4πt，单位为MPa；r为载荷圆形分布区域半径；(x0，y0)为圆心坐标；H(x,y)为Heaviside阶跃函数。

3.2方程求解

为满足边界条件，用三角级数形式表示板的挠度[15]，如下：

(15)

把载荷函数展开成三角级数：

(16)

根据三角函数的正交性，求得：

把式(14)代入上式，经过整理得到：

(17)

其中

(18)

式中A为载荷作用面围成的封闭区域。

将式(15)、式(16)拉氏变换后代入式(12)，经过整理后，得到：

(19)

即

(20)

对式(20)进行Laplace逆变换并代入式(15)，即可得到板的横向位移，如式(21)：

(21)

4　算例及参数影响分析

4.1Laplace积分变换及其逆变换的处理

文中需进行Laplace变换的参数较多，且表达式繁琐，故采用高斯-拉盖尔积分公式[16]进行数值求解。

由于式(21)较复杂，很难得到Laplace逆变换的解析解。因此，需用数值的方法进行求解。本文采用具有高精度的BURBIN F方法[17-18]，则tj时刻的横向位移W(x,y,tj)，可表示为

(22)

其中

由文献[17]可知，对于L×U=50～5 000时，cT∑=5～10时的计算结果较好。

4.2算例及结果分析

在MATLAB软件中，首先编写温度场模型，然后求解位移因子及温度相关的松弛模量，并采用高斯-拉盖尔积分公式进行Laplace变换，最后将拉氏变换后的相关参数代入式(21)，采用BURBINF方法进行逆变换，可得到时域下的板的横向位移。

以2层矩形板为例分析变温速率，初始温度对挠度的影响，除上述2个参数外，其余参数取值见表1。

变温速率为0 ℃/s时，不同初始温度下板的挠度变化，如图2所示。

对比不同初始温度下板挠度的变化幅值，可知：(1)由式(3)可知，松弛模量大小不仅受温度影响，而且与时间相关。从式(3)可看出，随着时间的增加，松弛模量不断减小，同时由热粘弹性本构方程(1)知，刚度矩阵各元素亦减小，从而引起多层板的承载能力降低，造成振幅的增加。因此，应力松弛模量越大，则板的振动幅度越小；松弛模量愈小，多层板的刚度愈小，承载能力愈低。(2)考虑到载荷变化规律为正弦曲线，多层板应首先达到向下的振动峰值后，经过约半个周期，才能产生此振动周期内向上的振动峰值。由于时间的推移，此时板的刚度已经小于上个峰值时的刚度，故随着时间的增加，板上下振动的幅度不相等。(3)由于温度越高材料的粘性特性越明显，刚度越低，因此初始温度较高时，板振动幅度较大，且不同温度下振动峰值到达时间不相同，温度较高时，稍微滞后。

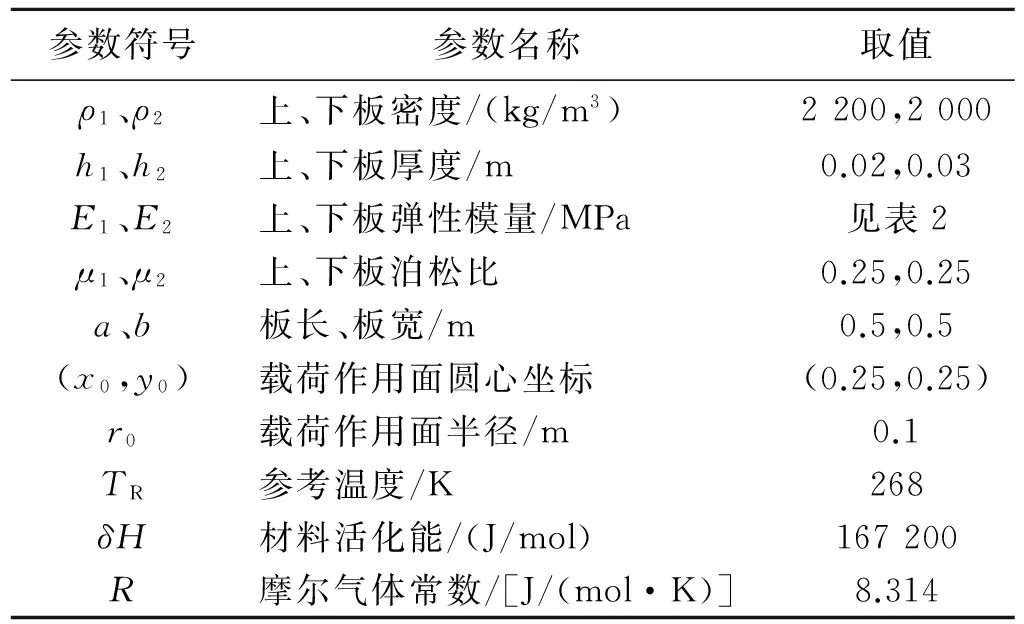
表1　参数取值

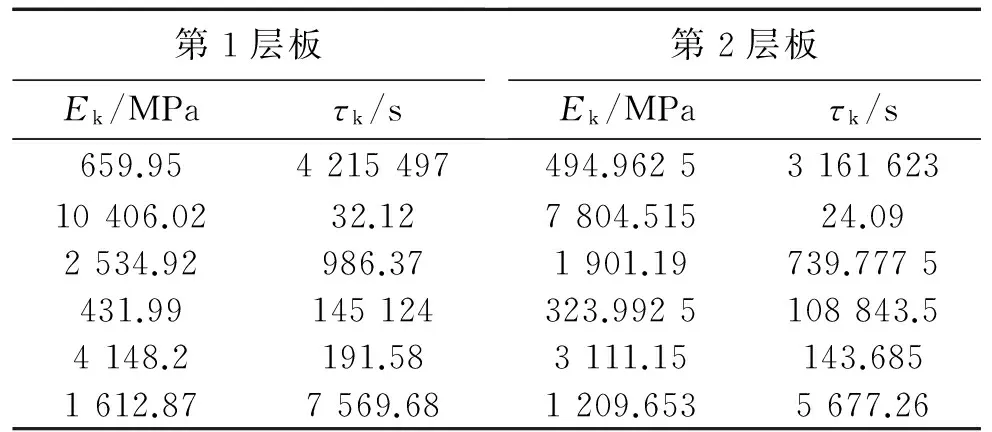
表2　Maxwell模型的参数取值

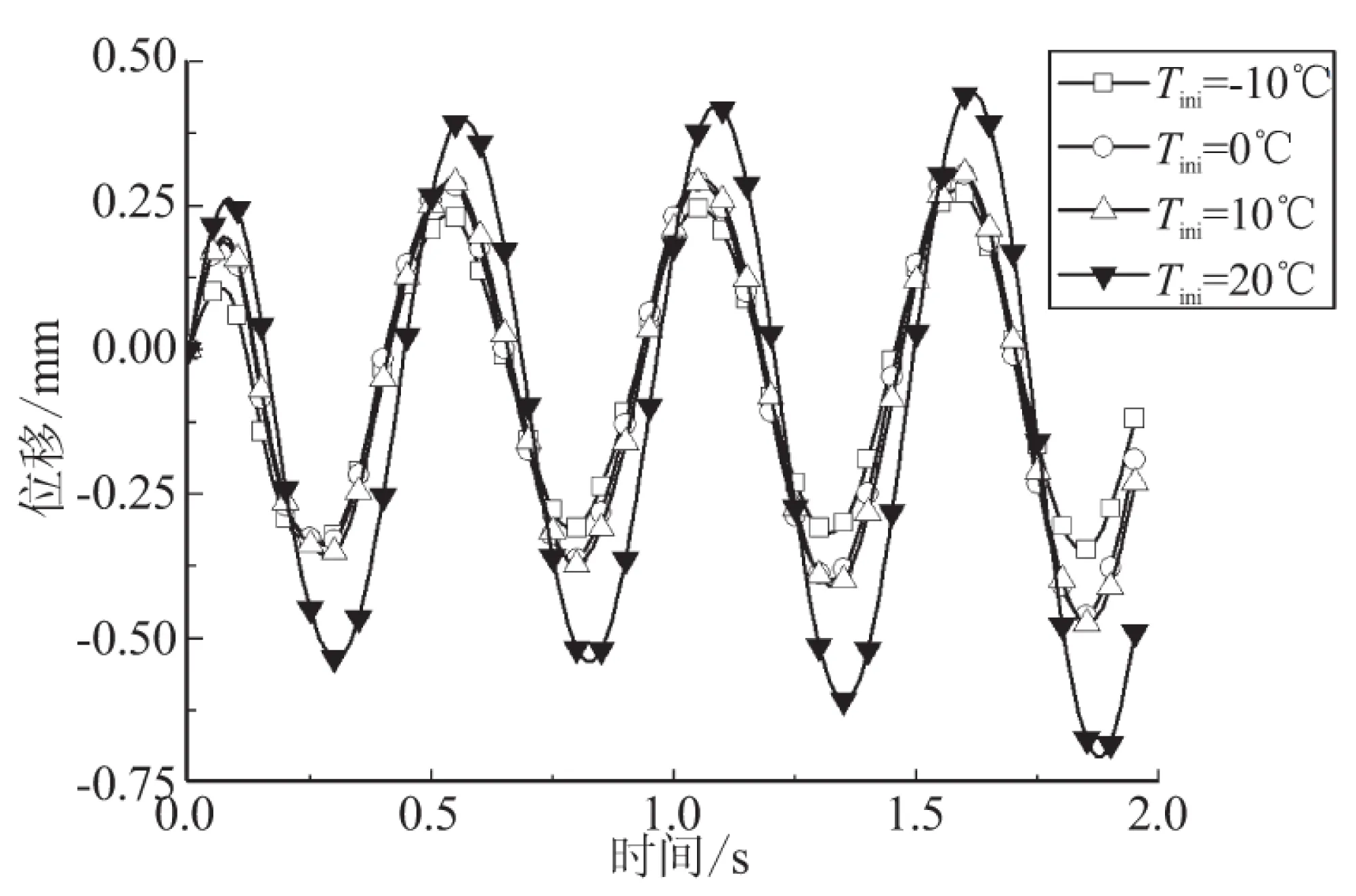
图2　不同初始温度下板的挠度

初始温度为10 ℃时，不同变温速率下板的挠度变化如图3所示。

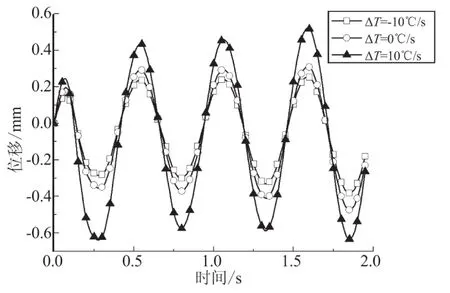
图3　不同变温速率下板的挠度

分析不同变温速率下板挠度的变化曲线，可看出：(1)变温速率越大，板的挠度变化幅值越大；(2)由式(5)及式(6)可知相同幅度的变温速率下，温度升高造成的松弛模量的减小量大于降温引起的松弛模量的增加量，就同幅度的变温速率导致的板刚度变化量而言，升温要大于降温。因此，相同的变温幅度下，温度升高对挠度的影响大于降温过程。

5　结论

采用热粘弹性本构模型及时-温等效原理，结合经典薄板理论，分析了温度载荷及圆形均布动载荷联合作用下多层粘弹性板的动力响应。研究得知，初始温度及变温速率对板的横向位移影响较大，对于粘弹性板的动力响应问题，温度是一个不可忽略的因素。

(1)初始温度越高，板的刚度愈低，导致多层板的挠度变化幅度越大。

(2)载荷作用时间越长，松弛模量越小，板的横向位移越大。

(3)变温速率越大，挠度变化幅度越大；由于板刚度的变化量在同幅度的变温速率下，升温要大于降温，故温度升高对挠度的影响大于降温过程。

[1]祝彦知, 薛保亮, 王广国. 粘弹性地基上粘弹性地基板的自由振动解析[J]. 岩石力学与工程学报, 2002, 21(1): 112-118.

[2]彭凡, 傅衣铭. 粘弹性板的非线性动力稳定特性分析[J]. 固体力学学报, 2004, 25(1): 115-118.

[3]傅衣铭，王永. 考虑损伤效应的粘弹性层合板的非线性动力响应分析[J]. 复合材料学报, 2005, 22(1): 114-119.

[4]傅衣铭, 汤可可, 王永. 变温场中具损伤粘弹性矩形板的非线性动力响应分析[J]. 固体力学学报, 2006, 27(3): 243-248.

[5]王燕楠, 李映辉, 邓一三. 含热传导效应粘弹性板耦合非线性动力分析模型[J]. 西华师范大学学报(自然科学版), 2008, 29(2): 117-121.

[6]李映辉, 王燕楠, 邓一三. 粘弹性板热机耦合非线性振动 (I)——动力学模型[J]. 四川大学学报(工程科学版), 2008, 40(5): 7-12.

[7]王燕楠, 李映辉, 邓一三. 粘弹性板热机耦合非线性振动 (II)——数值方法及结果[J]. 四川大学学报(工程科学版), 2008, 40(6): 69-74.

[8]Igor Bock. On large deflections of viscoelastic plates[J]. Mathematics and Computers in Simulation, 1999, 50: 135-143.

[9]Kim Tae-woo, Kim Ji-hwan. Nonlinear vibration of viscoelastic laminated composite plates[J]. International Journal of Solids and Structures, 2002, 39: 2857-2870.

[10]Assie A E, Eltaher M A, Mahmoud F F. Behavior of a viscoelastic composite plates under transient load[J]. Journal of Mechanical Science and Technology, 2011, 25(5): 1129-1140.

[11]Saeed Masoumi, Manouchehr Salehi, Mehdi Akhlaghi. Multiscale analysis of viscoelastic laminated composite plates using generalized differential quadrature[J]. Acta Mechanica Sinica, 2012, 223: 2459-2476.

[12]Zhou Yin-feng, Wang Zhong-min. Application of the differential quadrature method to free vibration of viscoelastic thin plate with linear thickness variation[J]. Meccanica, 2014, 49: 2817-2828.

[13]Raffaele Barretta, Raimondo Luciano. Exact solutions of isotropic viscoelastic functionally graded Kirchhoff plates[J]. Composite Structures, 2014, 118: 448-454.

[14]Dai Hong-liang, Li Li-qi, Liu Hai-bo. Thermoviscoelastic dynamic response for a composite material thin narrow strip[J]. Journal of Mechanical Science and Technology, 2015, 29(2): 625-636.

[15]颜可珍. 弹性地基上薄板的动力响应研究[D]. 杭州：浙江大学, 2005.

[16]李维真. 拉普拉斯变换的一种数值计算法[J]. 南京邮电学院学报, 1987, 7(4): 140-144.

[17]Urbln F. Numerical inversion of laplace transforms．an efficient improvement to dubner and abate's method[J]．The Computer Journal, 1973,17(4): 371-376.

[18]任瑞波, 谭忆秋, 张肖宁. FWD动荷载作用下沥青路面层状粘弹体路表弯沉的求解[J]. 中国公路学报, 2001, 14(2): 9-17.

(编辑：刘红利)

Dynamic response of viscoelastic multi-layer rectangle plates considering temperature effect

ZHANG Zhen-dong1, MA Da-wei1, REN Jie1, HE Qiang1, GAO Yuan2, WANG Xu2

(1.Nanjing University of Science and Technology，Nanjing210094，China；2.The Second Artillery Equipment Academy，Beijing100094，China)

On the basis of the thermoviscoelastic constitutive equation, time-temperature superposition principle and classical Kirchhoff thin plate theory, the motion differential equation of viscoelastic multi-layer rectangle plate with temperature was deduced. Then the expression of multi-layer rectangle plate deflection under circle distributed dynamic load and temperature was deduced by combing Laplace integral transformation and triangular series methods. The high-precision method of DURBIN F's numerical inversion of Laplace transforms was successfully used to evaluate the influence of initial temperature, the rate of temperature change on dynamic response of plate. Results indicate that the deflection of plate increases gradually as the value of initial temperature increases. With the increase of time, the deflection is increased too; the greater rate of temperature change, the more obvious magnitude of deflection variation; the effect of heating on deflection is greater than that of cooling under same magnitude of temperature change rate.

thermoviscoelastic constitutive equation；temperature effect；thin plate theory；dynamic response；inversion of Laplace transforms

2015-06-03；

2015-08-11。

装备预先研究项目(51328020106)。

张震东(1988—)，男，博士生，研究方向为兵器发射理论与技术。E-mail:zzd1157@163.com

任杰(1982—)，男，副教授，研究方向为兵器发射动力学。E-mail:renjie@njust.edu.cn

V414.3

A

1006-2793(2016)04-0542-05

10.7673/j.issn.1006-2793.2016.04.017