有限元分段反演优化方法测试固体推进剂的泊松比

张　晓，郑　坚，彭　威，顾志旭

(军械工程学院，石家庄　050003)



有限元分段反演优化方法测试固体推进剂的泊松比

张晓，郑坚，彭威，顾志旭

(军械工程学院，石家庄050003)

提出了一种通过准确测量载荷响应，利用ABAQUS有限元软件，对推进剂相应状态下的泊松比进行分段反演的测试方法。基于反演优化原理，建立了迭代模型和误差分析模型；测试了某型固体推进剂应力松弛下的泊松比，给出了测试过程和结果，分析了测量误差；利用时温等效原理，获得了泊松比变化主曲线；反演结果与光学非接触测量结果进行了对比，得到了反演误差，进一步验证了测试方法的有效性。

固体推进剂；有限元；分段反演优化；泊松比测试；应力松弛；主曲线

0　引言

泊松比研究的关键问题是泊松比的准确测定[1]。固体推进剂为近似不可压材料，一般取为接近于0.5的定值，但由于药柱结构性能对泊松比的取值非常敏感[2-3]，因此采用确定性的分析方法，得出的结果可信性较差[4]。固体推进剂泊松比是温度和载荷作用时间的函数，且很早就有人指出，泊松比的测量方法应能准确模拟推进剂的状态[5]。

传统引伸计法操作简单方便，但由于引伸计造成试件的附加变形，测试结果很难使人信服；有人建议，采用双激光杠杆引伸计[6]，测定试件变形，产生附加蠕变效应较小；非接触式的激光全息照相法和云纹干涉法[7]提高测试精度，但不适用于非线性材料和初始泊松比测量[8]；赵伯华[9]推导了泊松比与其他参数之间的表达式，间接求解了泊松比，但存在多个参数不能通过一次试验同时得到的问题。参数反演优化方法作为获取未知参量的有效方法，目前广泛用于众多工程领域，如地质工程[10-11]、土木建筑[12]、复合材料[13-14]以及光谱分析[15-16]等。然而，国内外至今尚无有关参数反演优化用于固体推进剂泊松比测试的报道。

本文针对上述问题进行研究，结合参数反演优化原理，提出一种通过准确测量载荷响应(位移、应力等)，利用ABAQUS有限元软件，对推进剂相应状态下的泊松比进行分段反演的测试方法；运用该方法测试某型固体推进剂应力松弛下的泊松比，揭示其变化规律，分析测量误差；与试验测量数据进行对比，结果基本一致。本方法实现了由载荷响应反演得到推进剂的材料参数，操作简单，测量准确，能进一步推广到蠕变或单向定速拉伸等条件下的泊松比测试，尤其适用于不易直接测量的场合，对进一步研究推进剂力学性能和药柱结构完整性具有重要意义。

1　测量原理

分段反演优化的基本思想是建立载荷响应与材料参数之间的理论模型，对载荷响应进行准确测量，利用有限元软件，将材料参数随时间变化的整个过程划分成多个时间段，分段运用参数反演优化方法进行迭代寻优，直到所取参数使得载荷响应的有限元计算结果与试验测量结果误差最小，所取参数值即为真值的最优近似。根据以上分段反演优化思想，本文将载荷作用过程进行划分，假设所划分段内泊松比不变，从而实现对泊松比取值的离散化，运用FORTRAN有限元语言编制用户子程序，分别进行满足边界和载荷条件的循环迭代运算，寻找能够使得有限元计算结果与试验测量结果误差最小的泊松比。此时，所取值即为泊松比真值的最优近似，视为此段实际泊松比，当段宽度趋近于零时，最优近似值将趋近于瞬时值，整个分段反演优化流程如图1所示。

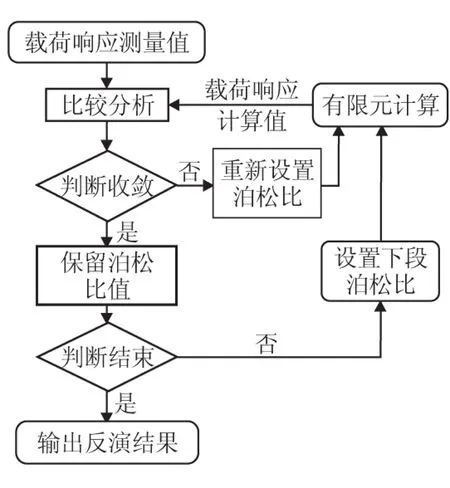
图1　分段反演优化流程图

2　数学模型

2.1迭代模型

加载条件不变的情况下，载荷响应是材料参数的函数，即

(1)

松弛模量E(t)为试验可得，因此有限元软件计算的结果仅依赖于泊松比的取值，即

(2)

分析整个加载过程，将测量时间点对应的泊松比 写成向量形式为

(3)

其中，N为时间段数，Xi为一个时间段内的泊松比向量。

将式(3)代入式(2)，得

(4)

对于任意段，令第j个测点的载荷响应试验测量值为Hje，有限元计算值为Hjs，m为测点数，建立段目标函数为

(5)

令νk+1=νk+Δν进行循环迭代，Δ2取得最小值时的ν即为泊松比反演的最优值。

2.2误差分析模型

分段反演方法的误差来源主要有测量误差、有限元模型误差、反演误差等，采用基于灵敏度计算的误差分析方法[17]，可获得反演参数的误差，具体分析如下。

对于整个加载过程，式(5)改写为

(6)

令Hjδ=Hje-Hjs为第j个测点总误差(包括测量误差、有限元模型误差、反演误差等)，将总误差Hδ写成向量形式为

(7)

假设νr为泊松比真值，νo为反演最优值，令νjδ=νjr-νjo为第j个测点上的泊松比反演误差，将Hj(νjr)在νjo附近作一阶泰勒展开为

(8)

令Hj(νjr)-Hj(νjo)=Hjδ，由式(8)可得

(9)

∂H(ν)/∂v即为灵敏度矩阵，由式(9)可得

(10)

为了求得泊松比的反演误差，关键工作是灵敏度矩阵的计算，下面推导有限元灵敏度矩阵计算过程。

有限元方程矩阵形式如下：

KU=F

(11)

由于F与v无关，方程两边对v求导可得

(12)

整理式(12)得

(13)

假设载荷响应函数H=SU，S为响应函数与位移的转换矩阵，则由式(13)得

(14)

为了求得∂H/∂v，关键是要求出∂K/∂v，由有限元基本原理可知

K=∭VBTDBdV

(15)

(16)

K可由有限元程序形成，文中S为应力矩阵，S=DB，因此，由式(14)～式(16)即可求得灵敏度矩阵，从而求出反演误差。

3　测试实例

3.1试验部分

试验的主要内容：(1)在70、50、20、0、-20、-40 ℃下，以500mm/min的拉伸速率，分别将6组试件(每组5个)单向等速拉伸至恒定应变5%；(2)记录应力松弛时间2、4、8、20、40、80、200、600、1 000s时的松弛力值。

采用标准哑铃型试件，标距70mm，截面10mm×10mm，用微机控制五头电子式万能试验机进行单向应力松弛试验。

3.2输入参数计算

对于松弛特性较弱的材料，松弛模量可按式(17)计算：

(17)

式中E(t)为t时刻的应力松弛模量，MPa；F(t)为t时刻的松弛力，N；ε0为初始恒定应变；A0为试件初始横截面积，mm2。

将松弛模量以Prony级数形式表示为[18]

(18)

其中，待定系数E∞、Ei和τi可通过最小二乘法拟合确定，取τi=τ110i-1。

对式(18)进行归一化处理，可得

(19)

参数E0、gi、τi为粘弹本构模型在ABAQUS中的输入参数。

3.3有限元模型及仿真

利用ABAQUS建立推进剂试件的有限元模型如图2所示。

图2　有限元模型

输入材料参数E0、gi、τi、ν进行仿真计算，其中泊松比ν即为待反演参数。

反演变量设置见表1。

表1　反演变量设置

3.4测试结果与分析

试验测得的不同温度下的松弛力见表2。

表2　不同温度下的松弛力

试验按照GJB 770B—2005严格执行，采用的试验机精度等级为0.5级，参数控制准确，系统误差小；操作过程基本由程序控制，且将多组测量结果取平均值，随机误差可忽略不计。因此，认为载荷响应测量准确。将不同温度下的应力松弛模量拟合成Prony级数形式，并分别进行归一化处理，可得有限元计算的输入参数，如表3所示。

表3　有限元输入参数

将参数输入ABAQUS中，建立有限元模型，使得边界以及载荷条件与试验条件相同，利用分段反演优化方法对推进剂的泊松比进行测试，结果如图3所示。

图3　泊松比反演结果

以上结果表明，随着温度的升高和载荷作用时间的增加，泊松比的值增大，且逐渐趋向于0.5。这是由于一方面随着温度的升高，推进剂中存在的主价力、次价力、界面之间的化学键力和物理吸附作用力等降低，推进剂的应变能力提高[19]；另一方面，随着加载时间的增长，推进剂的应变表现出延迟性。运用误差分析模型可得：泊松比反演误差<5×10-4，主要的误差来源：一是材料输入参数的拟合误差；二是有限元的模型误差。

利用时温等效原理，得到参考温度为20 ℃时泊松比随时间的变化关系，拟合成Prony级数形式为

103ν(t)=498.193 9-1.289 5e-0.0008019ξ-

2.142 3e-0.008019ξ-0.364 1e-0.08019ξ-0.188 2e-0.8019ξ

(20)

其中，ξ=t/aT为由温度T变到T0时的折减时间，T0为参考温度，aT为时温转换因子。

推进剂的时温转换因子可用WLF方程表示为[20]

(21)

式中T0为参考温度，K；C1、C2为材料参数。

文中T0=20 ℃，C1=3，C2=99，转换因子随温度的变化曲线，如图4所示。

同时，采用了光学非接触方法，根据粘弹性泊松比的定义，在相同松弛条件下，对推进剂泊松比进行了直接测量。

图4　转换因子变化曲线

粘弹性泊松比ν(t)表征在拉伸静载作用下，横向应变εy(t)对纵向应变εx(t)的响应[21]，可按式(22)计算：

(22)

纵向应变εx(t)可由上述试验机准确测得；横向应变εy(t)则由光学位移跟踪器测定，测试精度可达1 μm，主要误差来源：一是目标标定误差；二是因外界光强变化和震动产生的误差，以上均可通过多组测量取平均值的方法进行消除。

由于测试精度较高，可将多组直接测量结果的期望值作为泊松比真值，进行反演误差分析，可得：

依据时温等效原理，将试验测得的泊松比，绘制成参考温度为20 ℃的主曲线，与分段反演泊松比主曲线进行对比，如图5所示。

由图5可知，有限元分段反演测得的泊松比与试验测量结果具有较好的一致性，进一步验证了测试方法的有效性。

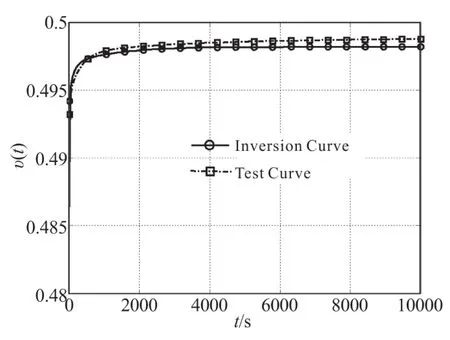
图5　主曲线对比图

4　结论

(1)有限元分段反演优化方法能准确简便地模拟固体推进剂的不同受力状态，以载荷响应测试试验为基础，能测量固体推进剂不同状态下的泊松比，结果具有实用性。

(2)测量了某型固体推进剂应力松弛下的泊松比，结果表明，随着温度的升高和载荷作用时间的增加，泊松比的值增大，且逐渐趋向于0.5，变化规律与理论分析相吻合。

(3)反演结果绝对误差均值为6.4×10-4，与误差分析模型所得结果一致，相对误差均值为0.13%，最大相对误差为0.2%，说明该方法是测量固体推进剂泊松比的有效途径。

[1]单桂芳,杨伟,冯建民,等. 材料泊松比测试方法的研究进展[J]. 材料导报,2006,20(3):15-20.

[2]雷勇军,袁端才,蔺文峰. 固体发动机药柱正交各向异性材料参数灵敏度分析[J]. 国防科技大学学报,2010,32(6):107-110.

[3]蒙上阳,唐国金,雷勇军. 材料性能对固体发动机结构完整性的影响[J]. 国防科技大学学报,2002,24(5):10-15.

[4]王君祺,职世君,张建伟. 非均布瞬态内压作用下固体推进剂药柱泊松比随机结构分析[J]. 固体火箭技术, 2012,35(6):747-750.

[5]Freudenthal M A. Solid propellant rocket research[M]. London: Academic Press Inc. ,1964.

[6]权铁汉,郝松林. 双激光杠杆/电测两用横向变形引伸计[J]. 仪表技术与传感器,1999(4):36-38.

[7]O'brien D J,Sottos N R,White S R. Cure-dependent viscoelastic poisson's ratio of epoxy[J]. Experimental Mechanics,2007,47(2):237-249.

[8]郝松林. 高填充复合推进剂的初始粘弹性泊松比[J]. 固体火箭技术,1996,19(4):46-50.

[9]赵伯华. 固体推进剂粘弹泊松比的研究[J]. 北京理工大学学报,1994,14(1):87-90.

[10]Nishimura S I,Nishiyama T,Murakami A. Inverse analysis of soft grounds considering nonlinearity and anisotropy[J]. Journal of the Japanese Geotechnical Society, 2005, 45(2):87-95.

[11]Hashash Y M A,Levasseur S,Osouli A,et al. Comparison of two inverse analysis techniques for learning deep excavation response[J]. Computers and Geotechnics, 2010, 37(3):323-333.

[12]黄东梅,朱乐东,丁泉顺,等. 超高层建筑等效静力风荷载的反演法[J]. 工程力学,2012,29(1):99-105.

[13]Anghileri M,Chirwa E C,Lanzi L,et al. An inverse approach to identify the constitutive model parameters for crashworthiness modelling of composite structure[J]. Composite Structures,2005,68(1):65-74.

[14]Kang Y L,Lin X H,Qin Q H. Inverse/genetic method and its application in identification of mechanical parameters of interface in composite[J]. Composite Structures,2004, 66(1):449-458.

[15]Van Beek J D,Meier B H,SchaFer H. Inverse methods in two-dimensional NMR spectral analysis[J]. Journal of Magnetic Resonance,2003,162(1):141-157.

[16]Yurko V. Inverse spectral problems for differential pencils on the half-line with turning points[J]. Journal of Mathematical Analysis and Applications,2006,320(1):439-463.

[17]尹铫,刘碧龙,白国锋,等. 激光测振有限元反演优化方法测量黏弹材料动态力学参数[J]. 声学学报,2013, 38(2):172-180.

[18]常武军,鞠玉涛,王蓬勃. HTPB推进剂脱湿与力学性能的相关性研究[J]. 兵工学报,2012,33(3):261-266.

[19]侯林法. 复合固体推进剂[M]. 北京: 宇航出版社, 1994.

[20]周光泉,刘孝敏. 粘弹性理论[M]. 合肥: 中国科学技术大学出版社,1996.

[21]赵伯华. 粘弹性泊松比与动态复数泊松比的研究[J]. 推进技术,1995,16(3):1-7.

(编辑：薛永利)

Measurement of solid propellant Poisson's ratio with the method of finite element piecewise inversion optimization

ZHANG Xiao, ZHENG Jian, PENG Wei, GU Zhi-xu

(Ordnance Engineering College, Shijiazhuang050003, China)

A novel method named finite element piecewise inversion optimization was developed for solid propellant Poisson's ratio measurement, which depended on the accurate load response test and the application of the finite element software ABAQUS. Based on the inversion optimization theory, iterative model and error analysis model were built. By means of piecewise inversion, the Poisson's ratio of a certain type of solid propellant was measured in the condition of stress relaxation, the process and results were provided with error analysis as well. Using the time temperature equivalence principle, the Poisson's ratio master curve was obtained. At the last, the inversion results were compared with optical non-contact measurement results while the errors were got, which further verified the effectiveness of this method.

solid propellant；finite element；piecewise inversion optimization；Poisson's ratio measurement；stress relaxation；master curve

2015-01-20；

2015-05-23。

张晓(1990—)，男，硕士，研究方向为固体推进剂力学性能。E-mail:erebuss@outlook.com

V512

A

1006-2793(2016)04-0519-05

10.7673/j.issn.1006-2793.2016.04.013