推进剂粘弹性泊松比测试的数字图像相关方法

申志彬，邓　斌，潘　兵

(1.国防科技大学 航天科学与工程学院，长沙　410073；2.北京航空航天大学 固体力学研究所，北京　100191)



推进剂粘弹性泊松比测试的数字图像相关方法

申志彬1，邓斌1，潘兵2

(1.国防科技大学 航天科学与工程学院，长沙410073；2.北京航空航天大学 固体力学研究所，北京100191)

固体推进剂是典型的粘弹性材料，其泊松比是时间的函数，相关标准中基于接触式测量方法的结果将推进剂泊松比视为常数，影响了药柱结构完整性分析的精度。针对此问题，推导了粘弹性泊松比的松弛型定义，提出了一种基于数字图像相关方法的固体推进剂泊松比高精度测量方法，研制了相应的测试系统，并测量了某HTPB推进剂的粘弹性时变泊松比。评估试验显示该测试系统的应变测量精度可达20 με，有效解决了推进剂泊松比千分位测不准的难题。结果表明，推进剂泊松比随松弛时间的增加而增加，具有明显的粘弹特性。所提方法可为粘弹性材料泊松比的高精度测量提供参考。

固体推进剂；粘弹性；泊松比；数字图像相关方法

0　引言

固体推进剂是典型的近似不可压粘弹性材料，其泊松比对发动机药柱的结构响应影响显著。特别是在内压载荷下，药柱近似不可压且处于三向受压状态，此时推进剂的泊松比每相对变化1%，可导致药柱的应力应变响应相对变化10%以上[1-3]。因此，若想实现固体发动机药柱结构完整性的精细分析，至少应将推进剂泊松比的测量精度精确到千分位，即有3位有效数字。

长期以来，因受限于测量技术水平，同时也为了简化问题，往往将固体推进剂等粘弹性材料的泊松比视为常数，并采用引伸计法等传统的接触测量方式测量推进剂的泊松比[4]。这样处理不可避免地会带来较大的测量误差。一方面，未考虑时间和温度对泊松比的影响；另一方面，固体推进剂模量较小，易变形，接触测量法会增加推进剂的附加刚度。采用该方法，最多只能将推进剂泊松比的测量精度精确到百分位，即只有2位有效数字。

许多学者针对推进剂泊松比的精确测量方法开展了研究。赵伯华[5]基于非接触测试方法，利用拉伸松弛模量试验和体积形变试验，通过模量和泊松比之间的积分关系式间接得到了推进剂的泊松比。何铁山等[6]直接模拟圆管发动机药柱在固化降温条件下的受力状态，间接测出了固体推进剂在该状态下的泊松比。郑健等[7]通过蠕变试验采用接触测量方式获得了推进剂的横向应变，并结合其松弛模量间接得到了推进剂的粘弹性时变泊松比。这些方法虽然不再将粘弹性泊松比视为常数，但多采用间接法或接触式测量方法，对推进剂泊松比的测量精度提高有限。

近年来，随着非接触式光测力学技术的不断发展，尤其是数字图像相关(Digital Image Correlation，DIC)技术的快速兴起，为准确测量粘弹性材料的变形提供了一种重要的测量手段。DIC方法具有简便、全场、准确等优点，在实验力学中备受青睐。理论上该技术可用于各种材料的变形和应变测量[8]，但在粘弹性材料中应用不多，目前还鲜有人将其应用于粘弹性材料泊松比的测试。

本文将DIC技术应用于推进剂泊松比的高精度测量，研制了推进剂泊松比高精度测试系统。并基于松弛型粘弹性泊松比定义，通过松弛试验，同时测得了推进剂的横向应变和纵向应变，获得了推进剂的时变粘弹性泊松比。

1　推进剂泊松比DIC测量方法

1.1粘弹性材料泊松比测量原理

粘弹性材料泊松比的测量方法可分为直接法和间接法两大类。其中，直接法通过测量试样的横向应变和纵向应变，并利用定义式直接计算材料的泊松比；间接法通过测量其他材料参数，如拉压松弛模量和剪切松弛模量等，利用泊松比与这些材料参数之间的关系式，通过数值转换间接得到泊松比。

由于间接法涉及不同的加载方式和试样，过程繁琐、操作复杂，且可能因多次测量误差累积而导致测量精度不高。此外，对于固体推进剂来说，限于当前的工艺和技术水平，材料参数离散程度较大，加载方式和试样的不同均会引入较大的测量误差。因此，间接法不适合固体推进剂的高精度测量，本文拟利用DIC技术采用直接法对推进剂泊松比进行高精度测量。

与线弹性泊松比不同，粘弹性泊松比是时间和温度的函数。关于粘弹性泊松比的定义，学术界有一定的争议，多数经典粘弹性力学教材中未明确给出粘弹性泊松比的定义式。有学者直接参照弹性泊松比的定义，将等温、各向同性粘弹性时域泊松比定义为[9]

(1)

式中εx(t)和εy(t)分别表示横向和纵向应变。

多数学者基于弹性-粘弹性对应原理，通过Laplace逆变换，得到了微分形式和积分形式的粘弹性泊松比的精确表达式[10-12]，这些表达式是间接法测试粘弹性泊松比的理论基础。

粘弹性泊松比ν(t)表征在静态拉伸载荷作用下，横向应变εx(t)对纵向应变εy(t)的响应。由于材料的粘弹特性，试件在外载荷作用下会产生松弛或蠕变[10]。因此，横向应变响应滞后于纵向变形历史，粘弹性泊松比是横向变形的一个记忆函数：

(2)

故粘弹性泊松比ν(t)不能由式(1)通过实测的εy(t)和εx(t)简单的代数运算求得。

令εy(t)=εy0H(t)，即试样处于松弛状态，则式(2)变为

(3)

式(3)即为通过松弛试验定义的粘弹性泊松比，它表示粘弹性泊松比为单位阶跃纵向应变所引起的横向应变响应。当然，通过蠕变试验、定速拉伸试验等也可给出粘弹性泊松比的表达式，但由于式(3)形式简洁、物理意义明确，因此国内外诸多学者均将其作为粘弹性泊松比的定义式[11-14]。Lakes和Wineman[11]通过研究表明，通过松弛试验和蠕变试验得到的粘弹性泊松比差异很小。此外，式(3)定义的粘弹性泊松比与松弛模量、蠕变柔量等粘弹性参数定义方式类似，这使得弹性-粘弹性对应原理自成一封闭体系。

本文基于式(3)，利用松弛试验通过DIC技术直接测量推进剂的粘弹性泊松比。

1.22D-DIC测量原理

DIC是基于计算机视觉技术的一种图像测量方法。通过对变形前后所采集的物体表面的2幅散斑图像进行相关性计算，以灰度为信息载体，通过搜索变形前后图像中对应图像子区并计算相关系数，将相关系数取极值时的子区作为目标子区，进而可计算出变形前后的位移值。获得全场位移后，可采用逐点局部最小二乘拟合法计算得到光滑连续位移场。在此基础上，再根据位移与应变之间的数学关系，可进一步求得全场应变。类似地，可得到各个时刻的全场应变分布。

由于本文研究对象可视为平面问题，采用二维数字图像相关方法(2D-DIC)进行图像测量。

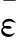
2　推进剂泊松比测试系统

2.1系统基本组成

基于2D-DIC测量原理，建立了一套非接触式的推进剂泊松比测试系统，该测试系统由微机控制电子万能试验机、推进剂试件和夹具及数据采集分析子系统等组成，如图1所示。数据采集处理子系统为系统核心，用于采集、控制，并对所获取的图像进行处理，利用2D-DIC技术获取推进剂试件的位移和应变信息，进而得到推进剂的泊松比。

图1　推进剂泊松比测试系统

数据采集分析子系统中的图像采集设备选用的是瑞士Baumer公司的TXG50工业数字CCD相机，其分辨率为2 448 pixels×2 050 pixels(500万像素)，像素灰度深度为8 bit，最大帧频是15帧/s。作为成像系统中最为重要的部分，镜头的选择往往决定测量精度。为满足高精度的测量要求，本系统选择了Schneider双远心镜头。该镜头的工作距离为195 mm，其视场为17 mm×14 mm，且具有±4 mm的远心深度，即被测物体在工作距离前后4 mm范围内变化时其放大倍数保存不变，能够有效克服实验中不可避免出现离面位移的面内变形测量结果的影响[15]。此外，在镜头前方装配了中心波长为450 nm的窄带通滤波片，并采用中心波长为450 nm的环形单色光源照明。这种单色光照明和带通滤波成像的主动成像方式[16]可有效避免环境光剧烈变化对成像系统所采集图像的影响，可获得亮度和对比度稳定的图像。

2.2测试系统精度评估

2.2.1系统精度评估方法

本系统测量推进剂的粘弹性泊松比，其本质是实现试件变形过程横向和纵向应变的准确测量，所以可通过评估该系统的应变测量精度来分析该推进剂泊松比系统的测量精度。针对硬质金属材料，目前的应变片测量精度可达到10 με左右，然而对于固体推进剂等软质材料，其模量仅有铝合金材料的万分之一，易受应变片附加刚度的影响，目前难以直接采用应变仪对其测量。因此，本文采用间接方法评估本系统的测量精度。

2.2.2系统精度评估试验

在小变形条件下，以硬质铝合金试件为研究对象，采用应变仪和所建推进剂泊松比测试系统，同时对试件在变形过程中的应变进行测量。试验用铝合金试件如图2所示，其宽度为10 mm，厚度为1 mm。预先在试件中央待测区域用黑色和白色的哑光漆制作好散斑，然后在大小为10 mm×20 mm散斑区域的正上方和正下方，分别沿拉伸方向粘贴好2个直角应变片。根据现场试验环境将2个测量子系统有序搭建起来，然后将该铝合金试件固定在试验机上。

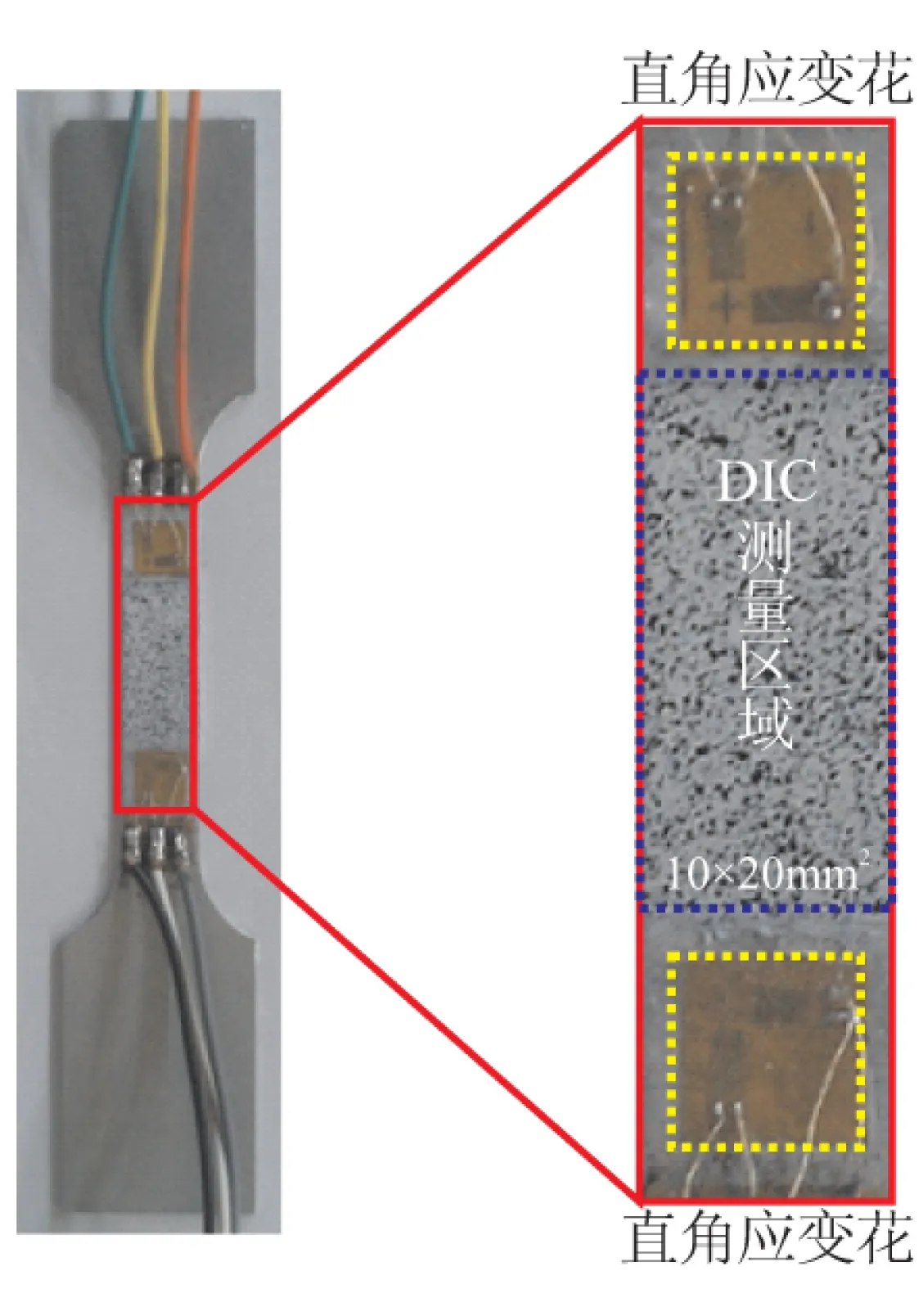
图2　铝试件上的应变片及随机散斑

试验时，试验机先以25 N/s的加载速率对试件进行单轴拉伸，当预载荷加至1 kN时，采集一幅图像作为参考图像，并将应变仪读数清零。随后按逐级加载方式进行试验，每加载0.25 kN(约90 με)时，拍摄并储存试件变形图像，同时记录应变仪的应变读数；当加载到3.75 kN(约1 300 με)时停止试验并卸载。由于应变片粘贴区域和数字图像测量区域均远离试件端部，由圣维南原理可知，这些区域的变形均可视为均匀变形，因而可通过比较分析与应变片所测应变结果的差异，进而实现对该泊松比测试系统测量精度的评估。

相比于应变片只能测得某一点的应变状态，2D-DIC法可根据变形图像获得计算区域内的全场位移和应变。图3给出了载荷为3.75 kN时的x和y方向位移场，可看出，采用2D-DIC方法所得2个方向的位移场均呈均匀分布，与单向拉伸条件下的实际位移分布相符。

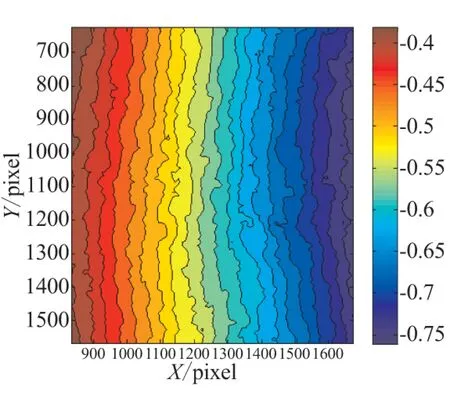
(a) 横向位移场

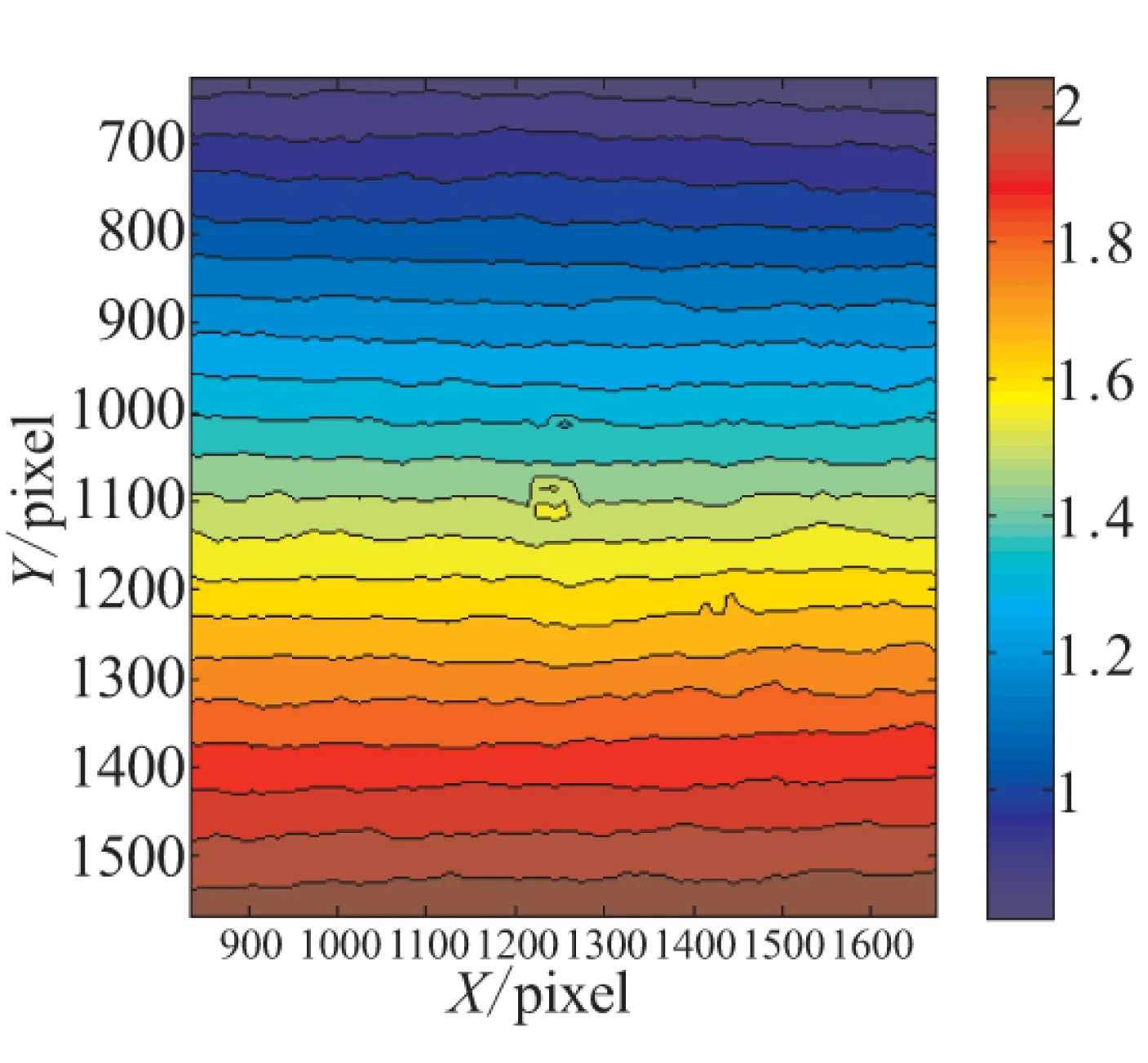
(b) 纵向位移场

2.2.3系统测量精度评估

基于得到的位移场函数和方程，采用逐点最小二乘法进行应变估计，可得整个计算区域的应变场。最后，将每个载荷下，整个计算区域在纵向和横向上的应变分别求平均值，以此作为在该计算区域内的应变值。

图4 (a)给出了2种不同测量方法下x和y方向正应变随载荷变化的对比曲线，可看出，2种不同测量方法所得应变结果非常接近。为了量化评估2D-DIC法的测量精度，图4 (b)给出了2D-DIC法相比应变仪法所测应变的偏差随载荷变化的趋势，由图可知，以应变仪法为基准，2D-DIC法测得x和y方向的应变偏差均在20 με范围内波动，即本系统的应变测量精度可达20 με。

可按照如下误差分析公式估计本系统泊松比测量精度：

(4)

其中，上标为“*”表示测量值；|Δεx|=20 με=20×10-6；对于松弛试验，按照标准，纵向应变εy一般取5%，由式(4)可得eν=0.4×10-3<0.5×10-3，即利用该系统所测得的推进剂粘弹性泊松比可精确到千分位。

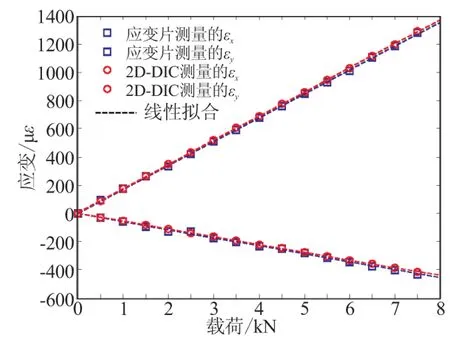
(a) 应变测量结果随载荷变化对比曲线

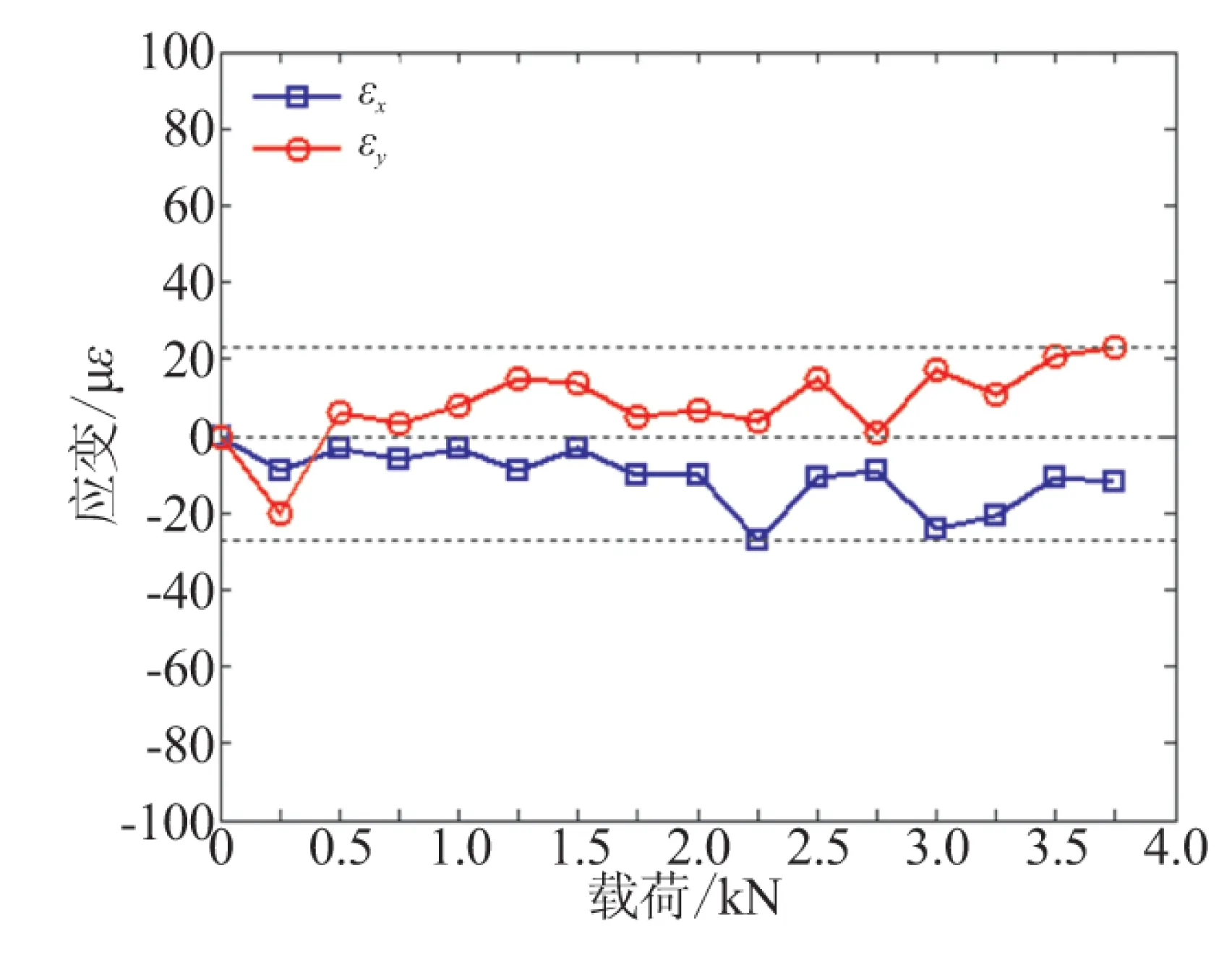
(b) 应变测量偏差随载荷变化曲线

不过该系统应变测试精度是以铝试件为对象并在良好环境条件下得到的。由于2D-DIC系统的测量精度容易受到其他随机因素(如镜头畸变、图像噪声、环境振动等等)的干扰，因此在推进剂泊松比试验中，须严格按照试验规范对图像进行采集与处理。

3　推进剂泊松比试验

3.1试验方法和步骤

根据2D-DIC系统的特点以及试验要求，推进剂泊松比试验的主要步骤如下:

(1)试件及其夹具

本文研究对象是某HTPB复合固体推进剂，试件和夹具的制作按照GJB 770B—2005《火炸药试验方法》[17]，采用标准的哑铃形试样。

散斑所提供的灰度信息是2D-DIC法相关计算的信息载体，因此散斑质量决定变形前后图像子区匹配的精度。良好的散斑图一般应具有随机分布、各向同性、高对比度等特点[18]。由于推进剂材质较软，直接在推进剂表面喷漆制作散斑可能会影响测试精度。考虑到固体推进剂主要成分颜色多呈白色、黑色或灰色，具有天然散斑的效果，因此无须专门制作随机散斑。

(2)系统安装调试

将推进剂哑铃形试件安装在试验机的夹头上，然后施加1 N的预载荷，并观察和调整试件状态，使试件天然散斑效果较好的一侧正对相机镜头，并确保试件在拉伸过程尽可能地满足单向受载状态。根据相机双侧远心镜头的焦距，初步确定相机与试件测量区域之间的工作距离。进一步，调整相机姿态，使其光轴与试件表面垂直。

打开光源，将其调至最大的散光状态，运行图像采集与处理软件，先将相机光圈调至最大，并根据显示器上图像的亮暗程度来调节光圈位置；微调相机工作距离，选择合适的曝光时间，直至形成明暗程度适中的清晰图像为止。

(3)试验机控制与图像采集

根据推进剂松弛试验中试件表面变形先快后慢的特点，设置图像采集频率。根据标准[17]，常温条件下推进剂松弛试验时间一般为1 000 s。因此，设定0～5 s的采集频率为10 fps，5～1 000 s的采集频率为0.05 fps，即每20 s采集一幅图。

采用位移和速度模式控制试验机夹头的移动，为模拟阶跃应变载荷，按照松弛试验标准[17]，以试验机最大拉伸速率500 mm/min进行加载，使得夹头一端产生2.5 mm恒定位移(即试件产生约5%的纵向应变)时，保持试验机夹头位置固定不变。

试验开始前，需要先采集一张未变形的图像，作为位移和相关计算的参考图像。试验开始时，同时启动图像采集程序和试验机。图像采集软件即按照设定的时间记录试验过程中试件测量区域散斑图像，并将其存入指定位置。

在图像采集过程中，由于外部环境的干扰以及图像采集系统的自身缺陷，使得所获得的原始图像往往在亮度、对比度和信噪比等方面存在某些不足，将这些原始图像直接用于图像相关性运算容易导致较大的计算误差。因此通常需要对原始图像做一些数据预处理，本文采用中值滤波方法对原始图像进行预处理。

3.2位移场拟合

对上述试验图像进行预处理后，即可采用数字图像相关软件基于亚像素插值技术实现计算区域全场位移的计算。

根据加载过程中的变形数字图像，以零时刻的图像作为参考图像，可依次计算得到试件测量区域在加载过程各个时刻的位移与应变信息。图5给出了测量区域在某时刻的位移场。从图5可知，在单向拉伸试验过程中，位于试件中央的测量计算区域的位移基本上呈均匀分布，符合单向拉伸条件下的位移分布状态。

(a) 横向位移场

(b) 纵向位移场

3.3推进剂的时变泊松比

由上述应力松弛试验，并利用2D-DIC法处理可得推进剂横向应变和纵向应变随时间的变化数据，按照1.2数据处理方法，计算得到推进剂粘弹性泊松比随时间的变化曲线，如图6所示。

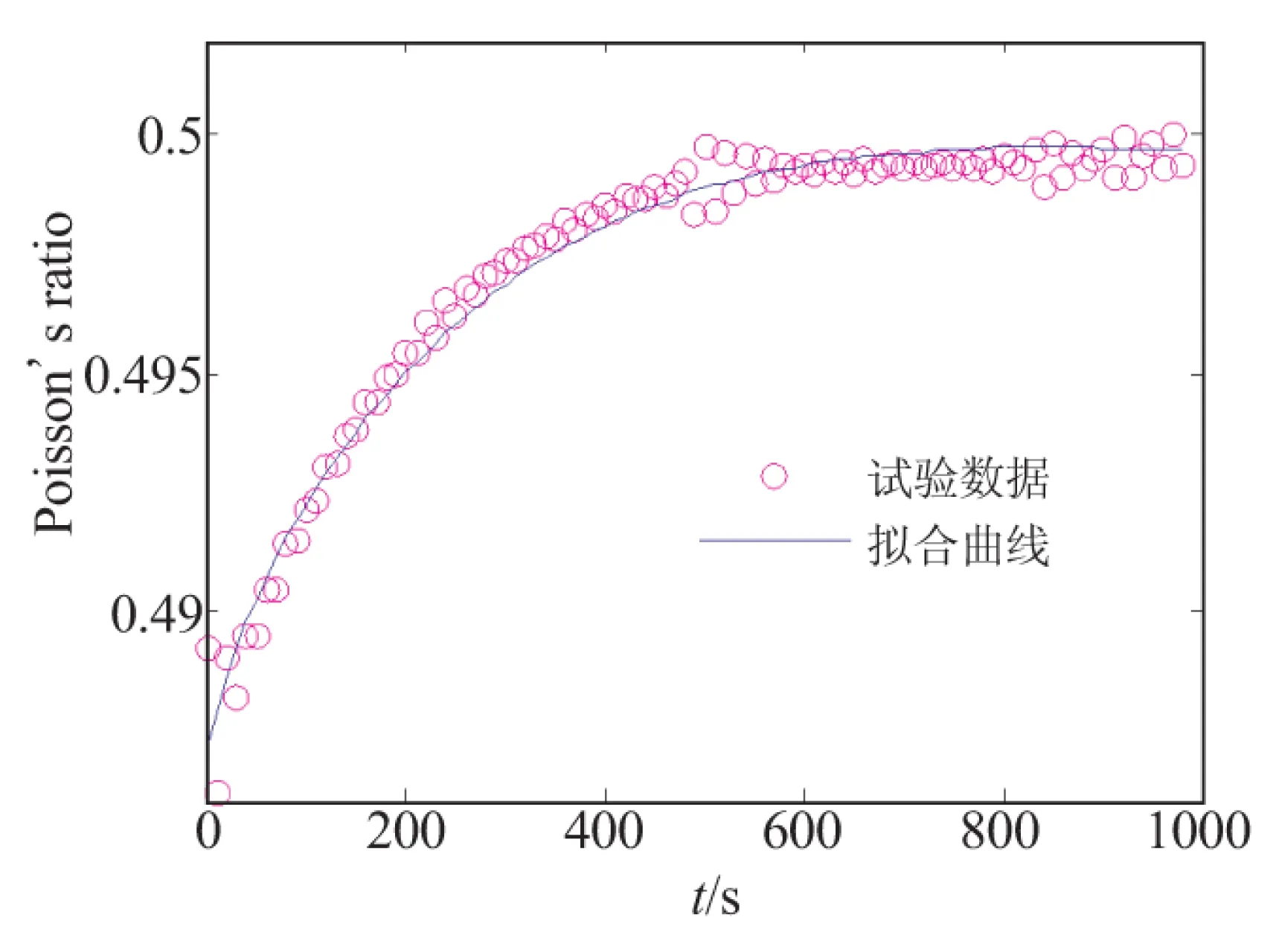
图6　推进剂泊松比随时间的变化曲线

图中拟合曲线是通过对离散数据采用非线性最小二乘法拟合成Prony级数形式得到的。拟合曲线与试验数据吻合较好，能较合理地反映粘弹性泊松比试验数据的变化趋势。可看出，随松弛时间增加，推进剂泊松比逐渐增大，并逐渐趋近于0.5。这说明推进剂是典型的近似不可压粘弹性材料，其泊松比是时间的函数，具有典型的粘弹性特征，将其视为常数与实际情况不符合。

4　结论

(1)松弛型粘弹性泊松比定义形式简洁，使用方便，可直接用于粘弹性泊松比的测量。

(2)所研制的推进剂泊松比测试系统应变测量精度可达20 με，能够将推进剂泊松比的测量精度精确到千分位，解决了推进剂泊松比千分位测不准的难题。

(3)推进剂泊松比随时间增加缓慢增大，趋近于0.5，具有明显的近似不可压粘弹性材料的特征。

[1]Chu H T, Chou J H. Poisson ratio effect on stress behavior of propellant grains under ignition loading [J]. Journal of Propulsion and Power, 2011, 27(3): 662-667.

[2]Chyuan S W. Studies of Poisson's ratio variation for solid propellant grains under ignition pressure loading [J].Journal of Pressure Vessels and Piping, 2003, 80(12): 871-877.

[3]蒙上阳, 唐国金, 雷勇军. 材料性能对固体发动机结构完整性的影响 [J]. 国防科技大学学报, 2002, 24(5): 10-15.

[4]QJ 3228—2005, 复合固体推进剂泊松比试验方法[S]. 中国航天标准化研究所, 2005.

[5]赵伯华. 固体推进剂粘弹泊松比的研究 [J]. 北京理工大学学报, 1994(1): 87-90.

[6]何铁山, 蒲远远, 王志强, 等. 圆管发动机法测定固体推进剂的泊松比 [J]. 推进技术, 2001, 22(2): 171-173.

[7]郑健, 张建彬, 周长省,等. 蠕变试验下固体推进剂泊松比研究 [J]. 南京理工大学学报, 2014, 38(5): 593-596.

[8]Pan B, Qian K, Xie H. Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review [J]. Measurement Scinece and Technology, 2009, 20(6): 062001.

[9]郝松林. 粘弹性泊松比的各种表述方法 [J]. 国防科技大学学报, 1992, 14(4): 7-12.

[10]赵伯华. 粘弹性泊松比与动态复数泊松比的研究 [J]. 推进技术, 1995, 3(3): 1-7.

[11]Lakes R S,Wineman A.On Poisson's ratio in linearly viscoelastic solids [J].Journal of Elasticity,2006,85:45-63.

[12]Tschoegl N W, Knauss W G, Emri I. Poisson's ratio in linear viscoelasticity-A critical review [J]. Mechanics of Time-Dependent Materials, 2002, 6: 3-51.

[13]M Christensen R. Theory of viscoelasticity [M]. Academia Press, 1982.

[14]牛秉彝, 王元有, 黄人骏. 高聚物粘弹及断裂性能 [M]. 北京: 国防工业出版社, 1991.

[15]Pan B, Yu L P, Wu D F. High-accuracy 2D digital image correlation measurements with bilateral telecentric lenses: error analysis and experimental verification[J]. Experimental Mechanics, 2013, 53(9): 1719-1733.

[16]Pan B, Wu D F, Xia Y. An active imaging digital image correlation method for deformation measurement insensitive to ambient light [J]. Optics & Laser Technology, 2012, 44(1): 204-209.

[17] GJB 770B—2005, 火药试验方法[S]. 国防科学技术工业委员会, 2005.

[18]张蕊. 数字图像相关及其在若干工程测试中的应用 [D]. 广州: 华南理工大学, 2011.

(编辑：吕耀辉)

Digital image correlation method for measuring viscoelastic Poisson's ratio of propellant

SHEN Zhi-bin1, DENG Bin1, PAN Bing2

(1.College of Aerospace Science and Engineering, National University of Defense Technology, Changsha410073, China;2.Institute of Solid Mechanics, Beijing University of Aeronautics & Astronautics, Beijing100191, China)

Solid propellant belongs to typical viscoelastic material, whose Poisson's ratio is the function of time. However, the occupation standards regard the propellant Poisson's ratio as a constant with the contact measurement, which have a bad influence on the accuracy of structural integrity analysis for grain. In this study, a relaxation definition of the viscoelastic Poisson's ratio was derived. A high precision measuring method for propellant Poisson's ratio based on Digital Image Correlation (DIC) method was proposed. Using this method, a measuring system for propellant Poisson's ratio was developed, and the time-varying viscoelastic Poisson's ratio of a certain HTPB propellant was measured. Test results show that the strain measuring accuracy of the system attains 20 με, which can solve the problem of milli-measuring inaccuracy for solid propellant Poisson's ratio. The results show that the Poisson's ratio increases with the time increasing, which exhibits obviously viscoelastic property. The present method is available for the noncontact measurement of other viscoelastic materials.

solid propellant；viscoelastic；Poisson's ratio；digital image correlation(DIC) method

2015-09-10；

2015-10-20。

中国博士后科学基金面上项目(2014M552684)；国家自然科学基金优秀青年科学基金项目(11322220)。

申志彬(1983—)，男，博士，研究方向为固体导弹结构完整性。E-mail:zb_shen@yeah.net

V512

A

1006-2793(2016)04-0513-06

10.7673/j.issn.1006-2793.2016.04.012