含铝凝胶燃料脉冲爆轰发动机工作过程瞬态特性

胡洪波，翁春生

(1.西安航天动力研究所 液体火箭发动机技术重点实验室，西安　710100；2.南京理工大学 瞬态物理国家重点实验室，南京　210094)



含铝凝胶燃料脉冲爆轰发动机工作过程瞬态特性

胡洪波1,2，翁春生2

(1.西安航天动力研究所 液体火箭发动机技术重点实验室，西安710100；2.南京理工大学 瞬态物理国家重点实验室，南京210094)

为了解含铝凝胶燃料脉冲爆轰发动机工作过程的瞬态机理，建立了含铝凝胶燃料脉冲爆轰发动机数学物理模型。采用守恒元与求解元数值计算方法，对单循环含铝凝胶燃料脉冲爆轰发动机流场进行了数值仿真，分析了其爆轰反应过程与冲量产生过程的瞬态特征。计算结果表明，爆轰波作用下，凝胶燃料液滴变化以剥离破碎为主，燃料液滴中铝颗粒随液滴剥离弥散于爆轰管内并参与反应，累积在最后阶段反应的铝颗粒较少。凝胶燃料爆轰燃气排放过程可划分为爆轰附着膨胀、燃气“壅塞”膨胀和膨胀减弱等3个典型特征阶段。研究结果对凝胶燃料脉冲爆轰发动机的应用研究具有参考意义。

脉冲爆轰发动机；凝胶燃料；爆轰；瞬态；数值计算

0　引言

为了更好地满足飞行器推进系统的需求，人们对先进推进技术的期待越来越强烈。在广大科研工作者对先进推进技术的探索过程中，由于凝胶燃料同时结合了固体燃料和液体燃料的许多优点，被认为是具有美好前景的未来推进燃料之一[1-3]。国内外学者对其流动、雾化与燃烧等进行了广泛研究[4]。

与缓燃波模式工作的推进系统相比，爆轰波模式工作的推进系统可获得更高的热循环效率[5]。为进一步提升推进系统性能，人们正致力于实现包括脉冲爆轰发动机(Pulse Detonation Engine, PDE)在内的以爆轰波模式工作的推进系统技术突破[6]。

将凝胶燃料与脉冲爆轰发动机相结合，可充分利用两者的优势，在开发新型高性能推进系统方面有着诱人的应用前景。虽然，目前国内外在脉冲爆轰发动机性能预测、数值模拟和实验研究方面开展了大量工作，但多以气相和液相燃料为主[7]，而较少采用凝胶燃料[8]。截至目前，尚未见到对含铝凝胶燃料爆轰进行数值仿真的报道。因此，本文通过建立含铝凝胶燃料与气相氧化剂多相爆轰模型，采用守恒元与求解元(conservation element and solution element,CE/SE)数值计算方法，对含铝凝胶燃料脉冲爆轰发动机爆轰流场进行了数值仿真，并对其爆轰反应过程和冲量产生过程进行了分析。

1　数学物理模型与计算方法

含铝凝胶燃料爆轰是耦合了气、液、固多相流动与燃烧反应的复杂物理化学问题，需进行合理简化，以建立适合求解的数学物理模型。

1.1模型简化与假设

根据凝胶燃料爆轰过程的特点，考虑凝胶燃料的非牛顿流体特性，将幂律模型(Power-Law Model，P-L模型)和液滴气动剥离的临界判据引入气液两相爆轰模型[9-10]，对爆轰管内以二氧化硅为凝胶剂的含铝凝胶燃料与气相氧化剂混合物多相爆轰过程，进行简化与假设如下：

(1)爆轰管内凝胶燃料、气相氧化剂混合物多相爆轰过程简化为轴对称无粘过程，即流场计算时不考虑粘性，而气体粘度及液滴非牛顿流体特性对液滴反应过程的影响，则在液滴剥离蒸发过程中加以考虑；(2)凝胶燃料液滴群单独作为液相，液滴为球形，且温度分布均匀；(3)爆轰管管壁绝热，不考虑热辐射对凝胶燃料液滴与铝颗粒的影响[10]；(4)凝胶燃料液滴表观粘度符合P-L模型；(5)将凝胶燃料液滴发生袋状破碎作为液滴剥离的临界判据；(6)凝胶燃料液滴仅在气流作用下发生剥离，液滴剥离部分所含液态汽油瞬间气化，所含铝颗粒群则分散于爆轰管内，并单独作为固相。同时假定铝以固态参与反应，不考虑反应过程中铝相变的中间过程；(7)凝胶剂在液滴中不发生相变，爆轰波作用下，液滴发生剥离，剥离部分的凝胶剂瞬间蒸发为气相；(8)将铝颗粒的燃烧产物氧化铝处理为气相方程中的一种组分，假定其温度、速度与气体相同，但对压力没有贡献[10]。

1.2数学方程

基于以上简化与假设，爆轰管内含铝凝胶燃料与气相氧化剂混合物多相爆轰的控制方程为

(1)

其中

总能E1计算为

(2)

式中Cvj(j=1,2,3,4,5,6,7)分别为氧气、二氧化碳、水蒸气、汽油蒸气、凝胶剂蒸气、氮气和氧化铝的定容比热容；Yj为对应组分的质量分数。

由于氧化铝对气相压力无贡献，压力p根据气相中除氧化铝之外的各组分分压力计算为[10]：

(3)

式中Wi(i=1,2,3,4,5,6)分别为氧气、二氧化碳、水蒸气、汽油蒸气、凝胶剂蒸气和氮气的相对分子质量。

总能E2、E3分别计算为

(4)

根据模型中对含铝凝胶燃料液滴剥离和蒸发过程的假设，凝胶燃料液滴剥离和蒸发对气相质量的贡献率m21计算为

(5)

燃料液滴剥离对固相质量的贡献率m23为

式(5)和式(6)中，含铝凝胶燃料液滴剥离与蒸发质量计算为

(7)

因剥离引起的液滴半径变化率计算为

(8)

式中μ为气体粘度；We为凝胶燃料液滴韦伯数；η为凝胶燃料液滴表观粘度；Wecr为临界韦伯数[11]。

因蒸发引起的燃料液滴半径变化率为[12]

(9)

式中λ为气体导热系数；Nu为努赛尔(Nusselt)数；T为温度；L为凝胶燃料液滴的蒸发潜热。

[6]和文献[10]，计算气相与液相、气相与固相铝颗粒群间轴向作用力Fx21、Fx31和径向作用力Fy21、Fy31以及对流传热Qconv、Qconv3。

含铝凝胶燃料爆轰过程中，同时存在汽油和铝粉颗粒。计算中，通过各自点火温度，控制其反应进程。汽油主要成分为辛烷，为简化计算，采用辛烷的化学反应方程式代替汽油的燃烧反应过程[12]，辛烷一步总包反应方程式为

aC8H18+12.5aO2+eN2

→8aCO2+9aH2O+eN2

(10)

不考虑铝的氮化，弥散于爆轰管内的固相铝颗粒与富氧空气燃烧反应的化学反应方程式为

4bAl+3bO2+eN2→2bAl2O3+eN2

(11)

铝颗粒燃烧反应中颗粒半径变化率为[13]

(12)

式中系数c0=2.36×106；活化能Eb=73.6 kJ/mol；Xeff为有效氧浓度；Ru为普适气体常数。

由于铝颗粒反应过程中不断产生与消耗，r3取为铝颗粒的体积平均半径，并由此计算铝颗粒数密度N3。

铝颗粒燃烧反应质量消耗率m31为

(13)

化学反应引起的汽油蒸气质量消耗率与气相中其他组分质量变化率由相应的化学当量关系式确定。

1.3数值计算方法

采用CE/SE方法，对控制方程进行离散求解，该方法将空间与时间作为同等变量，无需黎曼分解，在求解爆轰这种具有强间断的物理问题方面获得了成功的应用[9,12]。二维CE/SE方法离散格式与雅克比系数矩阵的详细推导见文献[14]。

由于化学反应的特征时间远小于对流的特征时间，方程(1)中的化学反应源项为刚性源项。因此，采用四阶龙格-库塔方法进行特殊处理[14]。

1.4边界条件与初始条件

含铝凝胶燃料PDE的计算模型为直径φ60 mm、长1.2 m的爆轰管，爆轰管一端封闭，一端开口。为了更准确地计算爆轰燃气排放过程，计算区域包括爆轰管内流场和适当区域的外流场[6]，计算网格宽度取为1 mm。考虑到轴对称性，计算区域为实际物理区域的一半，如图1所示。参考文献[6]，封闭端和壁面取为固壁边界条件，爆轰管出口取为出口边界条件，对称轴取为轴对称边界条件，外流场边界取为远场边界。

初始时刻，爆轰管内充满化学当量比的铝粉(球形当量直径2 μm)质量分数为60%、凝胶剂质量分数为4%的含铝凝胶燃料(燃料液滴粒径为100 μm)和氧气质量分数25%的富氧空气混合物，其初始压力与温度分别为0.1 MPa和288 K。以爆轰管封闭端的局部高温高压区作为初始点火条件。

图1　含铝凝胶燃料PDE计算模型

2　计算结果及其分析

如图2所示，随着爆轰波向爆轰管出口方向传播，爆轰压力增大，爆轰波传播速度增大，并趋于稳定。距爆轰管封闭端1.1 m处具有最高爆轰压力，压力峰值为3.85 MPa，爆轰波速度为1 906 m/s。如表1所示，基于C-J爆轰计算的该条件下压力峰值为4.36 MPa，爆轰波速度为1 957 m/s。可见，数值仿真结果与C-J爆轰计算结果吻合较好。

图2　爆轰管中心轴线上气相压力-时间曲线

表1　计算结果比较

从图2可知，0.1、0.3、0.5、0.7 m处的压力随着时间的变化均先迅速增大，随后快速降低到0.8 MPa附近的平台压力，并在维持平台压力一段时间后，再次降低。因距离爆轰管出口较近，爆轰波扫过之后，燃气膨胀迅速，距爆轰管封闭端0.9、1.0、1.1 m处的压力，随着爆轰波的到来，先迅速增大，到达各自峰值后，快速降低，不会形成压力平台。距爆轰管封闭端1.2 m的爆轰管出口位置的压力，随着爆轰波的到来，先迅速增大，到达3.41 MPa的峰值后，快速降低。由于爆轰管外无燃料，爆轰管出口处，受紧邻位置压力影响较小，膨胀较快，压力峰值降低。1.601 ms时刻，管口处压力降低至0.22 MPa。此后，由于爆轰管内燃气压力较高，管口气体为欠膨胀，管口压力变化很小。2.897 ms时刻，随着气体排出，爆轰管内压力下降，管口气体膨胀充分，管口压力再次降低。

2.1爆轰反应过程分析

图3、图4分别给出了爆轰管中心轴线上0.6 m处液滴半径与液相中铝颗粒质量分数，固相体积分数及其颗粒半径随时间的变化曲线。从图3可看出，液滴由初始粒径至完全消失所用时间为54 μs，0.442 ms时刻，液滴发生蒸发，液滴中铝颗粒质量分数开始增大，但增长速度缓慢。0.467 ms时刻，液滴中铝颗粒质量分数为61%，相对于0.442 ms时刻60%的初始值仅增加了1%。此后，由于液滴粒径减小及气相温度增大，液滴蒸发速率加快，液滴中铝颗粒的质量分数迅速增大。0.473 ms时刻，液滴中铝颗粒质量分数达83%。

图3　液滴半径与液相中铝颗粒质量分数

图4　固相体积分数及其颗粒半径

从图4可看出，随爆轰波的到达，液滴开始剥离和蒸发，弥散的铝颗粒使得固相体积分数增大。0.434 ms时刻，固相体积分数达到1.5×10-6的最大值后开始下降，该最大值对应时刻的铝颗粒半径为1 μm。0.438 ms时刻，固相体积分数降低为1.2×10-7，对应时刻的气相温度为2 170 K，铝颗粒半径为2.1×10-3μm。此后，在液滴剥离与蒸发引起的铝颗粒生成与燃烧引起的铝颗粒消耗的共同作用下，固相体积分数和铝颗粒半径分别维持在1.2×10-7和2.1×10-2μm以下。0.478 ms时刻，液滴消失并同时产生部分铝颗粒，使得固相体积分数与铝颗粒质量平均半径突然增大。

如图5所示，爆轰波到达初期，由于气液两相间速度差大，液滴剥离效应强，液滴半径变化率大。随着气液两相间速度差减小，液滴剥离效应减弱，液滴半径变化率减小。0.467 ms时刻，气液两相间速度差小，液滴剥离效应弱，液滴半径为29 μm(图3)，液滴蒸发效应显著增强，促使液滴半径变化率增大。由于液滴蒸发效应明显强于液滴剥离效应，液滴中铝颗粒体积分数增加(图3)。

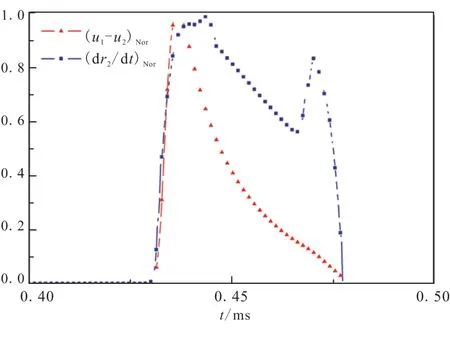
图5　无量纲气液相轴向速度差、液滴半径变化率曲线

2.2爆轰冲量特征分析

图7为爆轰管中心轴线上距封闭端0.5m处气相速度随时间的变化曲线。如图7所示，0.366ms时刻，在紧随爆轰波后的膨胀波作用下，气相速度迅速增大，并在0.380ms时刻，获得1 228m/s的峰值。

图6　二氧化碳生成过程中气相压力与温度的变化曲线

(14)

随后，由于紧邻位置(靠近爆轰管出口一端)处爆轰形成的反向压缩波，气相速度快速下降，0.609 ms时刻，气相在速度降为0后，开始向封闭端(逆向)流动。0.693 ms时刻，气相逆向速度达到最大值-39 m/s，并在封闭端反射的压缩波作用下开始减速。0.983 ms时刻，气相逆向速度降为0，气相正向速度开始缓慢增大，1.312 ms时刻，气相正向速度为6 m/s。此后，在爆轰管管口膨胀波作用下，气相再次膨胀加速，向爆轰管出口方向流动。

图7　爆轰管内距封闭端0.5 m处气相速度曲线

如图8所示，距爆轰管封闭端0.3、0.5、0.7 m处，由爆轰波后紧随的膨胀波引起的气相动量积分值依次为0.27、0.45、0.63 kg·m/s。可见，0.2 m内爆轰波后，膨胀波引起的动量积分值相同，均为0.18 kg·m/s，表明自持爆轰稳定后，爆轰引起的冲量值也是稳定的。

图8　紧随爆轰波后的膨胀波引发的动量积分曲线

图9为爆轰管中心轴线上1.2 m(管口)处气相速度随时间的变化曲线。从图9可看出，爆轰波扫过后，管口气相速度迅速达到1 491 m/s峰值后开始下降。与爆轰管内不同，由于没有受到爆轰波反向压缩效应的影响，管口气相速度没有快速下降到0，而是在降到883 m/s后就开始回升。1.613 ms时刻，气相速度增加到936 m/s。由于爆轰管内压力较高，燃气排放初期为“壅塞”流动，气相速度保持在936～945 m/s间的平台速度。随燃气排出，爆轰管内压力降低，2.725 ms时刻，管口气相速度为945m/s，随后气相速度开始下降。5.974 ms时刻，管口气相速度降为0，排放过程结束。

图9　爆轰管出口处气相速度变化曲线

根据文献[15]推力计算公式(式(15))，整个排放过程的冲量积分曲线如图10所示。

由图10可知，爆轰管排放过程的冲量增长表现为3个典型特征阶段。第1阶段(0.755～1.329 ms)，冲量曲线陡峭，冲量增长速度快，其末端时刻冲量积分值为2.67 N·s。因其膨胀过程由爆轰波后的膨胀波引起，将之称为爆轰附着膨胀阶段。第2阶段(1.329～2.815 ms)，排放处于“壅塞”流动阶段，冲量近似线性增长，该阶段产生的冲量为1.92 N·s。第3阶段(2.815～5.654 ms)，由于爆轰管内残余燃气不足，排放过程中管口压力降低，燃气排放过程表现为膨胀减弱阶段。该阶段燃气排放速度与密度均降低，冲量增长逐渐变缓，产生的冲量为0.98 N·s。

(15)

图10　爆轰管排放过程的冲量积分曲线

由式(16)计算的爆轰附着膨胀阶段、燃气“壅塞”膨胀阶段和膨胀减弱阶段的排气质量分别为1.59、1.50、1.10 g。3个阶段的平均排气温度依次为2 797、 2 275、2 089 K。可见，爆轰附着膨胀阶段和燃气“壅塞”膨胀阶段的排气质量约占排气总质量的74%。随着排气进行，平均排气温度逐渐降低。结合图2中1.2 m(爆轰管出口)处的压力-时间曲线可知，爆轰附着膨胀阶段和燃气“壅塞”膨胀阶段排气均处于欠膨胀状态。因此，仍可通过喷管等进一步降低排气温度。

(16)

3　结论

(1)数值计算结果与C-J爆轰结果符合较好，表明建立的模型能有效地模拟含铝凝胶燃料的爆轰。

(2)建立的模型可充分反映含铝凝胶燃料、富氧空气混合物爆轰过程中液滴、铝颗粒等的变化过程。爆轰波作用下，液滴变化以剥离破碎为主，凝胶燃料液滴中，铝颗粒随液滴剥离参与反应，累积在最后阶段反应的铝颗粒较少。由于液滴蒸发延迟，更多的燃料蒸气反应发生在波后气体膨胀的过程中。

(3)含铝凝胶燃料爆轰燃气排放过程可划分为3个典型特征阶段：爆轰附着膨胀阶段、燃气“壅塞”膨胀阶段和膨胀减弱阶段。

参考文献：

[1]Santos P H S,Carignano M A,Campanella O H.Qualitative study of thixotropy in gelled hydrocarbon fuels[J].Engineering Letters,2011,19(1):13-19.

[2] 强洪夫,刘 虎,韩亚伟,等.基于SPH方法的凝胶推进剂一次雾化仿真研究[J].固体火箭技术,2013,36(1):61-66.

[3] 刘香翠,张炜,朱慧,等.纳米铝粉及纳米铝粉/煤油凝胶体系能量性能研究[J].固体火箭技术,2005,28( 3):198-198.

[4] 李斌,张蒙正,周立新.凝胶推进剂应用研究进展[C]//大连:中国化学会第五届全国化学推进剂学术会议论文集,2011.

[5] Piotr Wolański.Detonative propulsion[J].Proceedings of the Combustion Institute,2013,34(1):125-158.

[6]Wang Ke,Fan Wei,Lu Wei,et al.Study on a liquid-fueled and valveless pulse detonation rocket engine without the purge process[J].Energy,2014,71(7):605-614.

[7]王研艳,翁春生.尾喷管构型对多循环两相脉冲爆轰发动机流场及性能影响[J].航空动力学报,2013，28(10):2256-2266.

[8]Palaszewski B,Jurns J,Breisacher K,et al.Metallized gelled propellants combustion experiments in a pulse detonation engine[R].AIAA 2004-4191.

[9]Wang G,Zhang D,Liu K,et al.An improved CE/SE scheme for numerical simulation of gaseous and two-phase detonations[J].Computers & Fluids,2010,39(1):168-177.

[10]洪滔,秦承森.爆轰波管中铝粉尘爆轰的数值模拟[J].爆炸与冲击,2004,24(3):193-200.

[11]Hsiang L P,Faeth G M.Drop deformation and breakup due to shock wave and steady disturbances[J].International Journal of Multiphase Flow,1995,21(4):545-560.

[12]彭振,翁春生.脉冲爆轰发动机中等离子体点火的数值计算[J].工程力学,2012,29(5):242-250.

[13]Fedorov A V,Khmel T A.Numerical simulation of formation of cellular heterogeneous detonation of aluminum particles in oxygen[J].Combustion,Explosion,and Shock Waves,2005,41( 4):435-448.

[14]翁春生,王浩.计算内弹道学[M].北京:国防工业出版社,2006.

[15]Hu Hong-bo,Weng Chun-sheng,Lv Xiao-jing,et al.Analysis on impulse characteristics of PDRE with exhaust measurements[J].International Journal of Turbo & Jet-Engines.2014,31(2):97-103.

(编辑：崔贤彬)

Transient characteristics for working process of pulse detonation engine with aluminized gelled fuels

HU Hong-bo1,2, WENG Chun-sheng2

(1.Science and Technology on Liquid Rocket Engine Laboratory,Xi'an Aerospace Propulsion Institute,Xi'an710100,China;2.National Key Lab of Transient Physics,Nanjing University of Science and Technology,Nanjing210094,China)

In order to understand the transient mechanism of pulse detonation engine with gelled fuels during the working process,the mathematical and physical model of pulse detonation engine with aluminized gelled fuels was established.The flow field of a single cycle pulse detonation engine with aluminized gelled fuels was simulated numerically by using the conservation element and solution element method,and the transient characteristics during the detonation reaction and impulse generation processes were analyzed.The calculation results show that the strip of the aluminized gelled fuels droplet under the detonation wave is predominant.The aluminum particles scatter into the detonation tube accompanying with the strip of droplets,and participate in reaction,so the aluminum quantity accumulated in the final stage is small.And the process of the gelled fuels' detonation exhaust can be divided into three typical stages,which are expansion stage attached to detonation,gas "choked" expansion stage and weaken expansion stage in sequence.The results have some significant

for application research on pulse detonation engine with gelled fuels.

pulse detonation engine;gelled fuels;detonation;transient;numerical calculation

2015-08-10；

2015-10-20。

国家自然科学基金(11372741)。

胡洪波(1987—)，男，博士生，研究方向为爆轰推进技术。E-mail：huhongbonjusteducn@163.com

V439

A

1006-2793(2016)04-0463-07

10.7673/j.issn.1006-2793.2016.04.003