超视距防空导弹中末制导交接班时的目标捕获概率研究

刘少波，赵良玉

(1.北京理工大学 宇航学院，北京　100081；2.北京电子工程总体研究所，北京　100854；3.飞行器动力学与控制教育部重点实验室，北京　100081)



超视距防空导弹中末制导交接班时的目标捕获概率研究

刘少波1,2，赵良玉1,3

(1.北京理工大学 宇航学院，北京100081；2.北京电子工程总体研究所，北京100854；3.飞行器动力学与控制教育部重点实验室，北京100081)

中末制导交接班时的目标捕获概率是超视距防空导弹作战过程中的一个重要指标。为了快速计算中末制导交接班时的目标捕获概率，通过将导弹和目标的三维空间散布转换为视线坐标系下弹目相对位置向量的均值和方差，建立了一种红外导引头中末制导交接班时的目标捕获概率解析计算模型，并利用蒙特卡洛方法验证了其有效性。以此模型为基础，采用正交试验方法完成了目标捕获概率的灵敏度分析，极差和方差分析结果均表明，导引头视场角对目标捕获概率的影响最显著，弹目相对位置向量在视线坐标系OyL轴和OzL轴上投影的方差次之。

防空导弹；中末制导交接班；目标捕获概率；正交试验；方差分析

0　引言

在新军事变革的牵引和推动下，超视距作战将是当下及未来防空导弹的重要模式和发展趋势，近年来的多次局部战争也很好地证明了超视距防空作战的必要性。复合制导是防空导弹实现超视距作战的重要基础，其基本思想是在导弹成功发射后，依据设定的中制导律接近并捕获目标，继而转入末制导飞行最终成功击毁目标。导引头在中末制导交接班时对目标的可靠捕获是末制导得以顺利实施的关键[1]，如何准确评估中末制导交接班时的目标捕获概率(也称为目标截获概率)是复合制导体制中的一项重要研究内容[2]。

采用蒙特卡洛方法进行大量的制导控制弹道仿真无疑是求取目标捕获概率的途径之一[3]，但这种方法需要建立完整的制导控制系统仿真模型，以及成千上万次的重复仿真才能得到较为可靠的结果。如文献[4]，针对不同的初始条件对导弹攻击目标过程进行蒙特卡洛仿真，根据置信水平选取仿真次数，并通过统计分析得到导引头捕获目标概率。制导控制系统完整模型在导弹总体方案设计阶段的不完备及其巨大的计算量一定程度上限制了该方法的应用范围。为了弥补蒙特卡洛方法计算目标捕获概率的不足，可采用目标指示误差来描述影响目标捕获概率的主要误差源，从而利用各误差的概率分布特点，通过一次弹道计算来获得目标捕获概率[5]。如文献[6]，假设目标指示误差服从瑞利分布，建立了导引头的角度捕获概率模型，并借助误差传递模型解算目标捕获概率。同样也可将影响目标捕获概率的各种误差源等效为导弹位置的散布和偏差，从而推导得到导引头开机捕获概率的计算模型和简化模型[7]。

本文以某型采用红外导引头的超视距防空导弹为研究对象，首先由弹目相对位置关系建立了目标捕获模型；接着给出了目标捕获概率的解析式近似计算模型，并采用蒙特卡洛方法验证了所建立模型的有效性；最后以此模型为基础对目标捕获概率进行了灵敏度分析。结果表明，红外导引头的视场角对目标捕获概率影响最显著，弹目相对位置向量在视线坐标系OyL轴和OzL轴投影的方差次之。

1　目标捕获误差及捕获条件

对于采用红外导引头作为敏感装置的末制导体制而言，目标捕获只需考虑角度捕获和距离捕获即可[8]。超视距防空导弹在中末制导交接班时的目标捕获概率主要受以下不确定因素的影响[7]：

(1)导弹位置、姿态和速度的不确定性：导弹初始值装定误差、惯导仪器测量误差、指令的延迟等均可能造成中末制导交接班时的导弹位置、姿态和速度偏差。

(2)目标位置、姿态和速度的不确定性：地面观测站的测量误差、目标的机动飞行、目标运动预测误差等因素将造成中末制导交接班时的目标位置、姿态和速度偏差。

(3)导引头指向不确定性：导引头的安装误差、陀螺漂移误差及光学系统测量误差、伺服机构误差和导引头内部各部件的不一致等因素将造成中末制导交接班时的导引头指向存在一定偏差。

综合考虑以上偏差，中末制导交接班时的导引头目标捕获模型可示于图1，图中X、μ分别为弹目相对位置的向量及其期望，D0为导引头的指向分布中心向量，D为导引头实际指向向量，εL为弹目视线误差角，εd为导引头实际指向和实际弹目相对位置向量的夹角，φd为导引头指向误差角，φdd0为导引头实际指向与导引头指向向量分布中心向量的夹角。

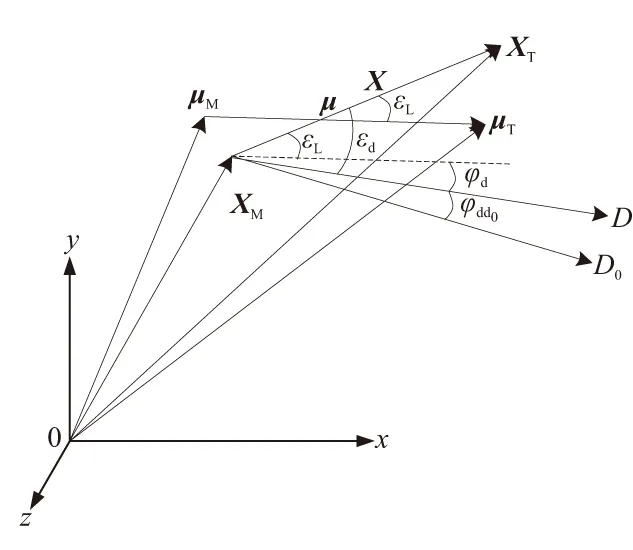
图1　导引头捕获目标示意图

将导弹和目标在地面坐标系下的实际位置向量XM和XT分别为

导弹和目标的位置分布中心μM和μT分别为

将红外导引头在中末制导交接班时成功捕获目标需要满足的距离捕获和角度捕获条件描述如下：

(1)距离捕获：弹目间的距离R小于等于导引头最大捕获距离Rsmax；

(2)角度捕获：εd小于等于导引头视场角αf。

2　目标捕获概率模型

为了便于建立目标捕获概率的解析式模型，基于图1做如下合理假设：

(1)导弹和目标在空间中服从三维正态分布；

(2)假设导引头自身的伺服系统可修正其指向误差，即假设εd=εL。

则由红外导引头中末制导交接班时的捕获条件可得目标捕获概率为

(1)

将导弹和目标所服从三维正态分布的概率密度函数分别写为

式中BM和BT分别为导弹和目标位置的误差协方差矩阵。

由正态分布的性质，弹目相对位置向量X也将服从正态分布，且其均值μ和协方差矩阵B可分别写为

则弹目相对位置向量X的概率密度函数为

(2)

将式(2)代入式(1)，即得红外导引头的目标捕获概率表达式为

从式(3)和积分性质可知，当αf或者Rsmax增大时，积分区域变大，式(3)的积分结果也会变大，即捕获概率P和αf、Rsmax正相关。

需要指出的是，在式(3)的推导过程中，设计者需要知道的信息为中末制导交接班时的导弹散布信息和目标散布信息。其中，导弹的散布信息由研制人员提供，可保证准确性；而目标的散布信息取决于攻击方对其性能的了解程度及对其运动状态的监测和预测精度，难免存在一些偏差，但从统计学的角度来讲，可适当放宽方差的要求，对获得较为可靠的目标捕获概率计算结果影响较小。

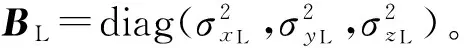
为求取积分(3)，可用面积相等的椭圆域

考虑一般情况下存在σyL≈σzL，可将式(3)最终写为

(4)

其中

式(4)即为本文推导得到的红外导引头在中末制导交接班时的目标捕获概率解析表达式。为书写方便，下文略去下标L。和蒙特卡洛方法计算目标捕获概率相比，完成一次目标捕获概率的解算可能需要进行多达800次的导弹攻击过程蒙特卡洛仿真[4]，而本文提出的解析模型只需要知道μx、σx、σy、σz、αf、Rsmax的值即可通过式(4)求得目标捕获概率，大大减少了计算量。

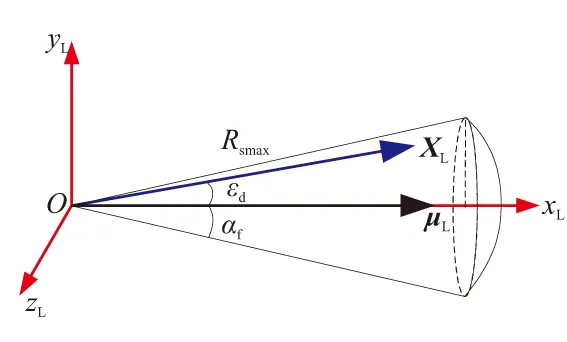
图2　视线坐标系下的积分区域

同时，由式(4)可看出，影响目标捕获概率的因素主要包括μx、σx、σy、σz、αf、Rsmax，但由于式(4)是高度非线性的，很难直观判断各因素对其影响的显著程度，下面在完成该计算模型的验证后将通过数值仿真方法来分析各因素对目标捕获概的影响程度。

3　目标捕获概率模型验证

和基于制导控制弹道计算目标捕获概率的蒙特卡洛方法不同，将用于验证式(4)有效性的蒙特卡洛仿真方法描述如下：依据给定分布的μx、σx、σy、σz，可生成n个服从三维正态分布的向量，若该向量落在指定区域内的次数为m，则导引头的目标捕获概率为

取αf=3°、Rsmax=8 km、σy=σz=120 m、μx=6 km，当σx从1 m取到500 m，分别采用蒙特卡洛方法(结果记为P1)和式(4)计算目标捕获概率(结果记为P2)。其中，蒙特卡洛方法在每一个σx处进行100 000次的数学仿真，2种计算方法的结果如图3所示，图4为本文建立的目标捕获概率近似模型与蒙特卡洛方法的计算结果残差。从图3和图4可见，式(4)的计算结果和由蒙特卡洛方法获得的计算结果趋势相同，2种方法的残差数量级为10-3，解析表达式的计算结果准确性可以接受。

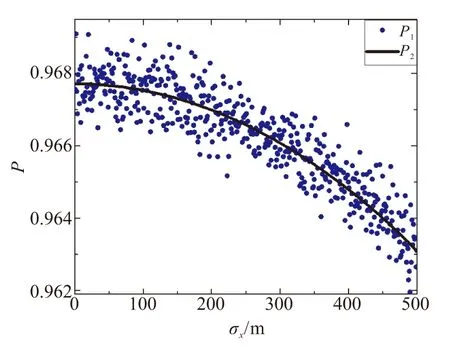
图3　蒙特卡洛方法和解析式计算结果对比

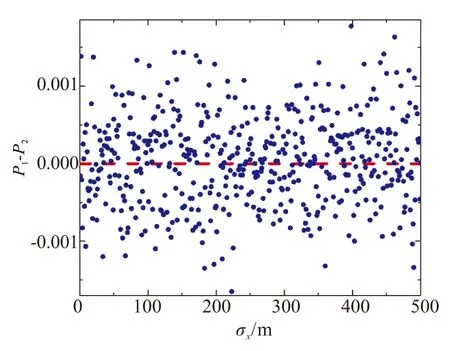
图4　蒙特卡洛方法和解析式计算结果的残差

图5是其他变量不变时目标捕获概率P分别随αf、Rsmax、μx、σy的变化趋势，其中蒙特卡洛方法的计算结果记为P1，式(4)的计算结果记为P2。从图5可见，一方面，2种方法的计算结果相差不大，证明了式(4)的正确性，另一方面可结合图4定性分析各因素对目标捕获概率的影响情况：位置误差σx、σy、σz的增大会导致P减小，且σy、σz的(其中σz的影响等同于σy，图5中不再列出)影响明显大于σx；随着μx增大P先增大，但当μx大于最大捕获距离后，P急剧减小；当最大捕获距离在μx的3σ之内时，P随Rsmax增大而增大，在此范围外基本不受影响；P随αf增大而增大并趋近于1.0。

4　目标捕获概率灵敏度分析

4.1正交试验设计

为进一步定量分析μx、σx、σy、σz、αf、Rsmax对中末制导交接班时目标捕获概率的影响，找出影响最显著的因素，设计正交试验来进行仿真和灵敏度分析[9]。以某型采用红外导引头的超视距防空导弹为例，将上述每个因素取5水平，得到因素水平表如表1所示。

本实验为6因素5水平实验，可选用L25(56)标准正交表[10]。正交表和采用近似目标捕获概率计算模型式(4)计算得到的目标捕获概率如表2所示。

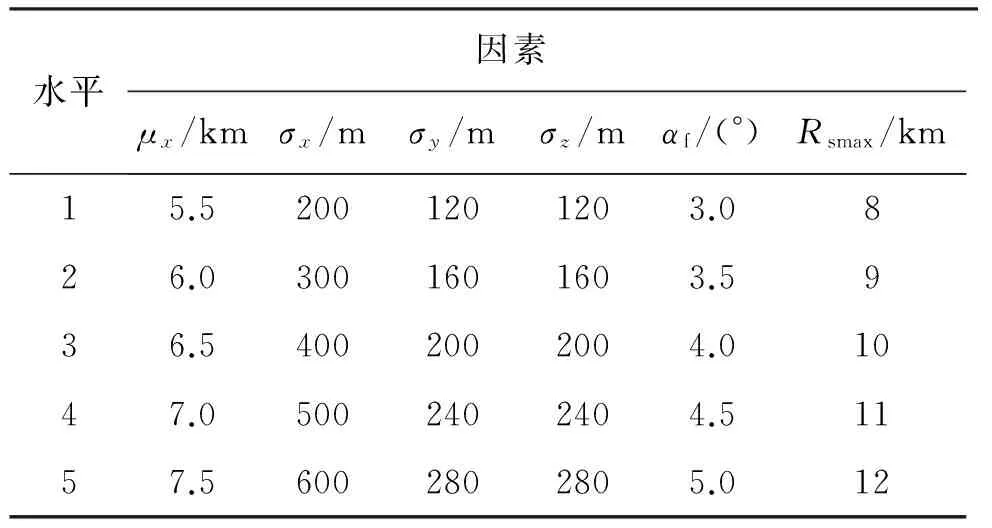
表1　因素水平表

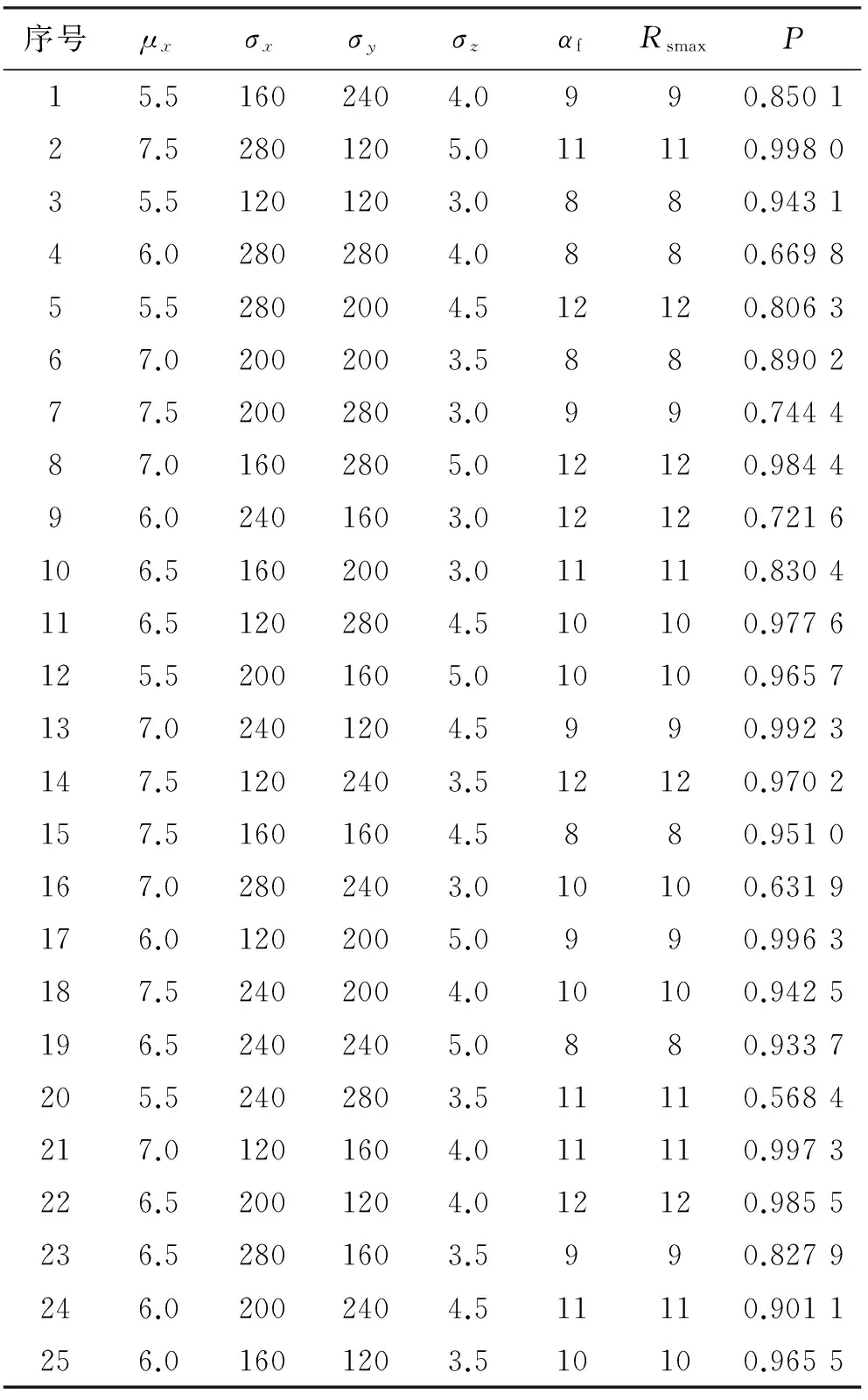
表2　正交试验结果

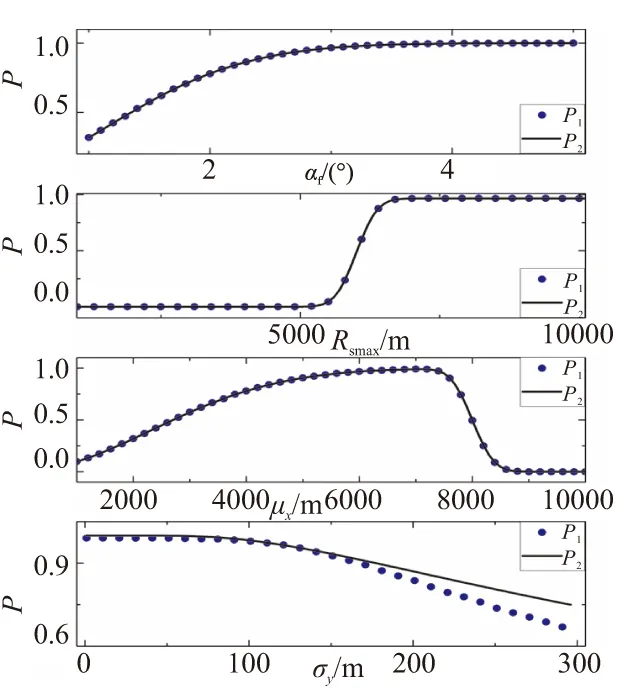
图5　目标捕获概率的变化趋势

4.2极差分析

极差R反映了各因素水平变动时，试验指标的变动幅度，R越大，则这个因素对试验指标的影响也越大。故可依据R的大小，来判断影响因素的主次[11]。

设因素μx所在列为Ti(1)，且ti(1)(i=1,2,3,4,5)的计算公式为

(5)

则极差的计算公式为

(6)

式中μxi代表μx第i个水平的取值；j代表第j个因素。

μx、σx、σy、σz、αf、Rsmax利用式(5)和式(6)可计算得到表3。由表3最后一行的数据可看出，αf对目标捕获概率的影响最大，其次是σy和σz，μx和σx更次之，Rsmax对目标捕获概率的影响最小。各因素与捕获概率的趋势如图6所示，可看出αf越大，捕获概率越大；αy和σz越大，捕获概率越小。各因素的最优水平分别为5、1、1、1、5、3，对应各因素的值分别为μx=7.5 km、σx=200 m、σy=σz=120 m、αf=5°、Rsmax=10 km。

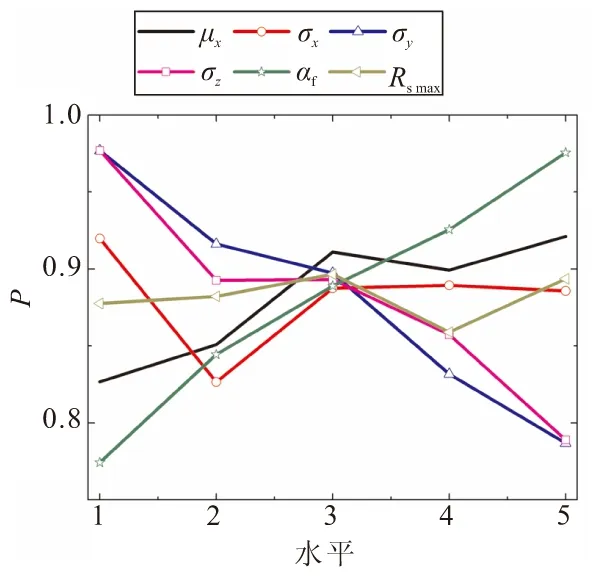
图6　各因素水平与捕获概率的变化图

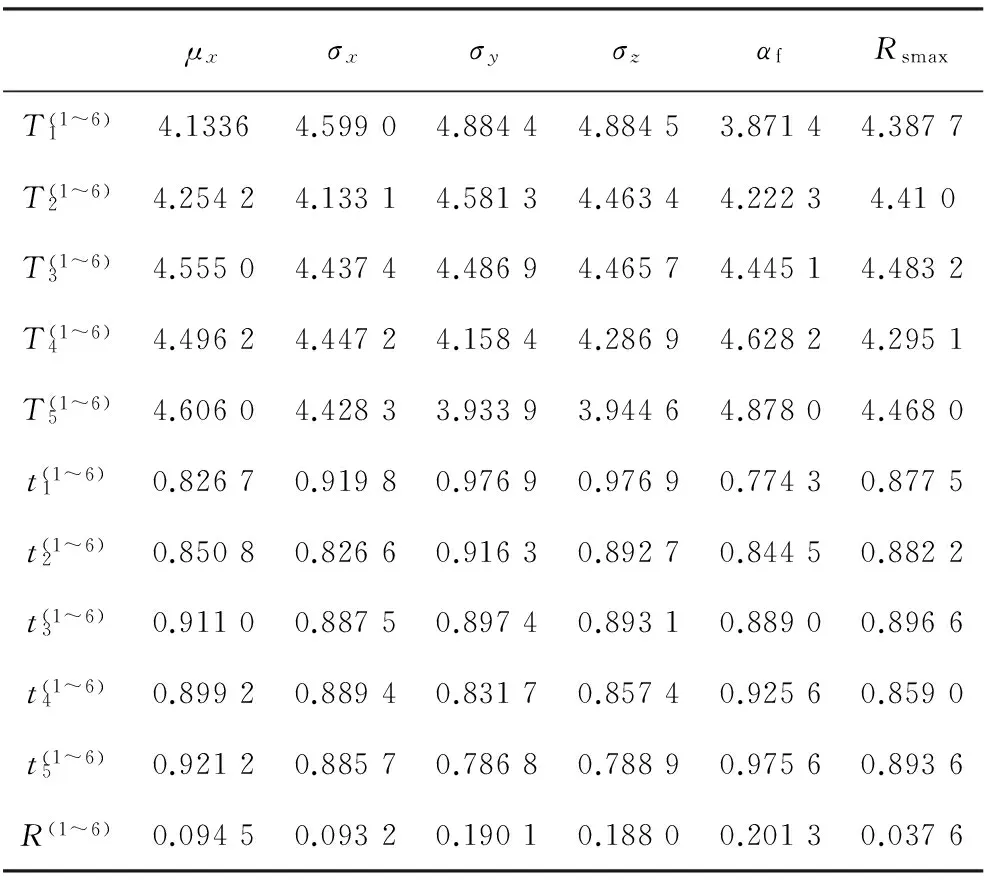
μxσxσyσzαfRsmaxT(1～6)14.13364.59904.88444.88453.87144.3877T(1～6)24.25424.13314.58134.46344.22234.410T(1～6)34.55504.43744.48694.46574.44514.4832T(1～6)44.49624.44724.15844.28694.62824.2951T(1～6)54.60604.42833.93393.94464.87804.4680t(1～6)10.82670.91980.97690.97690.77430.8775t(1～6)20.85080.82660.91630.89270.84450.8822t(1～6)30.91100.88750.89740.89310.88900.8966t(1～6)40.89920.88940.83170.85740.92560.8590t(1～6)50.92120.88570.78680.78890.97560.8936R(1～6)0.09450.09320.19010.18800.20130.0376

4.3方差分析

极差分析简单有效，但它不能估计误差的大小，即不能精确的估计哪些因素对试验指标有显著影响，特别是对于水平数大于等于3且需要考虑交互作用的试验，极差分析法有其局限性[11]。方差分析可用于检验多组样本均值间的差异是否具有统计意义，以弥补极差分析的不足。

方差分析的基本原理是用总偏差平方和SST来表征25组样本间的捕获概率与其总均值偏差的和，总偏差平方和的计算公式和总自由度fT分别为

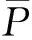
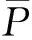
式中r为任一列上各水平出现的次数；m为各因素水平数。

二是误差平方和，为25组样本的目标捕获概率与其相应水平的目标捕获概率均值偏差的和，用于表征组内差异，其计算方法和自由度fe为

式中k为因素个数。

本试验次数n=25，总自由度fT=24，各因素及误差自由度分别为4和0。为估计试验误差，增加一组试验：σy=σz=600 m、σx=600 m、αf=3°、Rsmax=8 km、μx=7.5 km，对应的目标捕获概率为0.482 1。则总试验次数变为26，各因素及误差自由度分别变为4和1，得方差分析结果如表4所示。

表4　方差分析结果

根据各因素的偏差平方和可知，各因素影响重要程度排序为αf>σy>σz>μx>σx>Rsmax。方差分析结果与极差分析结果一致。

从方差分析结果还可看出，视线坐标系下弹目相对位置向量的均值、其在OxL方向的方差及导引头的最大捕获距离这3个因素对应的均方差很小，说明对试验结果的影响很小，这些小的均方差通常可作为误差处理，同时将相应的自由度也并入误差自由度，从而提高误差估计的精度。将μx、σx、Rsmax并入误差，得到误差e′。根据显著性分布表得F0.05(4,13)=3.18，可看出导引头视场角和弹目相对位置向量在OyL方向的方差是显著因子，即它们对目标捕获概率的影响显著。

5　结论

(1)通过将导弹和目标的三维空间散布转换为视线坐标系下弹目相对位置向量的均值和方差，建立了一类超视距防空导弹中末制导交接班时的目标捕获概率解析计算模型，利用蒙特卡洛方法验证了其有效性。该解析模型大幅度降低了目标捕获概率的计算量，可用于工程实践中快速计算中末制导交接班时的目标捕获概率。

(2)以本文建立的目标捕获概率模型为基础，采用正交试验方法完成了目标捕获概率的灵敏度分析，极差和方差分析结果均表明，导引头视场角对目标捕获概率的影响最显著，弹目相对位置向量在视线坐标系OyL轴和OzL轴上投影的方差次之，弹目相对位置向量的均值、其在OxL方向的方差及导引头的最大捕获距离的影响较小。

[1]刘骁, 唐胜景, 朱大林, 等. 制导弹药末段目标截获概率研究[J]. 兵工学报, 2015,36(2): 287-293.

[2]张鑫, 张丕旭. 防空导弹中末制导交班成功概率评估方法[J]. 四川兵工学报, 2013,34(2): 41-44.

[3]秦荣华. 远程攻击末制导目标截获概率数字仿真[J]. 上海航天, 2005(3): 26-28.

[4]赵晓睿, 高晓光, 张建东. 主动雷达型空空导弹截获概率分析[J]. 飞行力学, 2002,20(3): 59-62.

[5]樊会涛. 复合制导空空导弹截获目标概率研究[J]. 航空学报, 2010,31(6):1125-1129.

[6]谢希权, 易华. 多目标攻击空空导弹的目标截获概率分析[J]. 电光与控制, 2001(2): 33-36.

[7]张大元, 雷虎民, 李海宁, 等. 复合制导导引头开机截获概率估算[J]. 固体火箭技术, 2014,37(2): 150-155.

[8]李友年, 王霞, 李记新, 等. 无数据链情况下红外空空导弹射后截获概率研究[J]. 四川兵工学报, 2013,34(10): 4-7;15.

[9]唐明南, 张维刚, 宋海凌, 等. 防空导弹武器中末制导交班灵敏度分析[J]. 现代防御技术, 2012,40(2): 36-40;64.

[10]王岩, 隋思涟. 试验设计与MATLAB数据分析[M]. 北京: 清华大学出版社, 2012.

[11]Weiss M, Bucco D. Handover analysis for tactical guided weapons using the adjoint method [C]//AIAA Guidance, Navigation, and Control Conference and Exhibit,2005: 6157.

(编辑：吕耀辉)

Target acquisition probability at hand-off from midcourse to terminal guidance of a BVR air defense missile

LIU Shao-bo1,2，ZHAO Liang-yu1,3

(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing100081, China; 2.Beijing Institute of Electronic System Engineering, Beijing100854, China;3.Key Laboratory of Dynamics and Control of Flight Vehicle, Ministry of Education, Beijing100081, China)

The target acquisition probability is an important parameter at hand-off from midcourse to terminal guidance of a beyond visual range (BVR) air defense missile. In order to calculate the target acquisition probability with low computational cost, the distributions of the missile and the target in three-dimensional space were transformed to the mean and variance of relative range vector in line-of-sight coordinate firstly, and then an analytical model was established to calculate the target acquisition probability of a kind of missile with an infrared seeker. After the analytical model was verified by the Monte Carlo method, it was employed to investigate the sensitivity of the target acquisition probability by means of orthogonal experiments. The results of range analysis and variance analysis both prove that the influence of seeker field angle on the target acquisition probability is dominated, and influences of variances of projections of relative range vector alongOyLandOzLdirection in line-of-sight coordinate are the second.

air defense missile；hand-off from midcourse to terminal guidance；target acquisition probability；orthogonal experiment；variance analysis

2015-06-19；

2015-07-20。

国家自然科学基金(11202023)。

刘少波(1994—)，男，硕士生，研究方向为飞行器总体设计。E-mail:1120113088@bit.edu.cn

赵良玉(1981—)，男，博士/副教授，研究方向为飞行器总体设计。E-mail:zhaoly@bit.edu.cn

V448

A

1006-2793(2016)05-0723-06

10.7673/j.issn.1006-2793.2016.05.022