基于事件触发机制的推力矢量控制伺服控制系统设计

李国梁，张合新，扈晓翔，孙　鹏，周　鑫

(第二炮兵工程大学 控制工程系，西安　710025)



基于事件触发机制的推力矢量控制伺服控制系统设计

李国梁，张合新，扈晓翔，孙鹏，周鑫

(第二炮兵工程大学 控制工程系，西安710025)

针对航天器控制制导系统的数字化，扁平化设计中通信资源紧缺问题，提出一种事件触发伺服控制系统设计方法。方法依据跟踪输出变化偏差决定数据采样和信息传递，较传统周期采样方法能够明显降低总体采样次数，从而可有效降低通信资源的消耗。将由事件触发引入的输出变化偏差视为干扰，事件触发伺服控制系统可建模为仅考虑输入输出的受扰系统，利用受扰系统理论推导出系统稳定跟踪的线性矩阵不等式(LMI)条件，可方便地实现触发机制的设计。仿真结果表明，较周期采样方法，事件触发方法可节约通信资源77.5%以上。

事件触发控制；伺服控制；系统设计；触发机制设计

0　引言

随着新型航天器柔性发射任务的需求日趋激烈，航天器控制制导系统的数字化、模块化和扁平化设计已成为一种发展趋势[1]。无论是在基于总线构成的航天器，还是更为广义的基于通信网构成的航天器，系统中单元节点是直接挂在总线上或接入通信网[2]，要求各节点对通信资源的消耗尽量减少，同样对航天器用于推力矢量控制的伺服机构控制也提出类似要求。为了减少控制中对通信资源的消耗，事件触发控制[3-4](Event-triggered control，ETC)方法受到学者们的关注。ETC是一种可在通信资源极度匮乏情况下使用的控制策略。在事件触发控制中，信号采样、控制量计算和信息传递等一系列控制任务的执行由精心设计的事件触发机制决定。基本思想是只有系统工作在偏离期望状态达到一定程度时，触发机制才发出事件，然后执行相应的控制任务，而不像传统的周期采样控制方法，控制任务的执行是在固定的时间间隔周期地执行。研究表明[3-10]，事件触发控制能在有效减少采样或控制任务执行数量的同时，保持良好的控制性能。特别是基于状态反馈的事件触发控制，由于其易于分析特点，首先受到研究人员的青睐[5-6]，相对来讲，易于工程实现的输出反馈ETC方法成果相对较少[7-10]。

航天器中用于推力矢量控制的伺服机构控制系统设计，为一实际工程案例，其系统的所有状态并不能够轻易获得，研究基于输出反馈的控制方法更具实际应用价值，目前关于其控制系统设计主要研究热点的是控制系统数字化设计以及鲁棒控制器的设计[11]，还没有成果考虑数字化控制设计中节约通信资源的问题，而这一问题又是在数字化和网络化飞行器控制制导系统设计中必需要重视的问题，特别是系统比较庞大复杂时。

鉴于以上分析，本文以某型航天器推力矢量控制电动伺服机构作为被控对象，研究采用输出反馈的事件触发伺服控制(ETSC)实现通信资源节约问题。首先，将系统建模为受扰系统模型的形式；然后，利用受扰系统稳定理论，分析系统的稳定性以及触发条件参数设计问题。

1　问题描述

1.1周期事件触发伺服控制系统描述

某型航天器推力矢量控制中，俯仰或偏航单方向运动的电动伺服机构2自由度伺服系统支配方程为[11]

(1)

(2)

(3)

(4)

(5)

式中U、L分别是电动机电枢电压和电流；R、L分别是电动机绕组电阻和电感；θm为电动机轴的输出转角；θ1为负载的输出转角，其他参量定义可参考文献[11]。

为了提升研究的针对性，忽略工程中的不确定性和非线性因素，忽略干扰力矩，消去中间变量θm，可得如下方程组

(6)

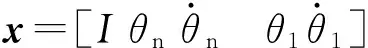
(7)

z=Csxs

(8)

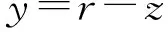
(9)

其中，x为被控对象的状态；u为控制输入；r为参考输入；z为跟踪控制输出；y为跟踪误差。

方程中对应的系数矩阵为

系统采用如下的控制可实现有效跟踪：

(10)

u=Ccxc

(11)

本文研究采用图1所示的事件触发输出反馈控制实现伺服控制问题。

图1　输出反馈事件触发控制系统示意图

假定控制器输出到被控对象的信息传递不受任何限制，即不存在时延、宽带和量化等因素的影响；而被控对象的测量输出到动态控制器输入端的采样和信息传递，要受到事件触发器的控制，即图中虚线部分，其含义是只有事件触发时刻tk时，才执行采样和信息传递，事件触发时刻由如下触发机制决定。

(12)

其中，σ为触发机制参数；ez(t)为被控对象上一采样时刻输出和当前输出偏差：

(13)

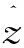
(14)

对应式(10)动态反馈控制器也变为如下形式：

(15)

1.2相关知识

受扰系统理论是一种非线性系统稳定性分析的理论[13-14]，下面给出有关该理论的一些基本知识。

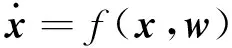
(16)

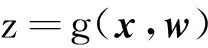
(17)

其中，x∈Rn为系统状态，输入w∈Rm，z∈Rl为系统标量输出，需要指出的是这里的w是一种广义的输入，可泛指任何形式的输入，一般认为w是一种干扰信号，系统式(16)、式(17)也被称为受扰输出系统。对于这类系统，输入非零时，系统全局渐进稳定一般难以满足。所以，采用更为一般的稳定概念，即输入到输出之间的属性来刻画系统特性，如L2增益稳定。信号v的L2范数定义为

定义1系统式(16)、式(17)输入到输出的L2增益γ定义如下：

(18)

其中，x(0)∈Rn为初始状态；β为一确定函数；w(t)能量有界输入,即w(t)∈L2空间。

引理1如果存在连续可微二次函数V:Rn→R对所有的Z∈rl和w(t)∈Rm满足：

(19)

则系统式(16)、式(17)从输入w到输出z以小于等于γ的L2增益稳定。

本文的研究思路是将由式(7)、式(8)和式(11)～式(15)构成的事件触发控制系统描述为式(16)、式(17)的受扰输出系统形式，然后利用引理1，分析系统的L2稳定性以及确保系统稳定的触发机制式(12)中参数σ的选择问题。

2　系统建模

(20)

则事件触发控制问题可转化为以上系统输入e到输出z的L2稳定问题。

图2　输出反馈ETC系统等效示意图

3　结果

定理1系统(20)对事件触发引入的偏差e(t)输入到输出z以小于等于γ的L2增益稳定的条件是，存在对称矩阵P>0满足如下线性矩阵不等式：

(21)

证明：令V(x)=xTPx)，显然V(x)为连续可微二次函数，L2稳定条件式(19)变成如下形式：

结合系统模型(20)，上式变为如下形式：

=(xTAT+eTBT)Px+xTB(Ax+Be)

=xT(ATP+PA)x+eTBTPx+xTPBe

又因

显然式(21)成立就能确保式(19)成立，也就保证了系统(20)e到z的L2稳定，证毕。

定理2对于事件触发伺服控制系统式(7)、式(8)和式(11)～式(15)，当σ=1/γmin时，能够获取最大触发间隔，且实现有效跟踪。其中，γmin为定理1条件成立时的γ最小取值。

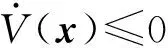
4　数值仿真

以式(7)～式(11)描述的伺服控制系统为对象，使用文献[11]参数，采用式(12)～式(15)描述的事件触发控制方法，进行如下3个方面的仿真验证。

4.1数值仿真

仿真目的是验证定理1和定理2的正确性。仿真分2步：一是利用Matlab LMI工具箱编写代码求解定理1中线性矩阵不等式优化结果，寻找使线性矩阵不等式可行解存在的最小参数γ；二是所得结果设计触发机制，设置非零的参考输入，验证事件触发跟踪控制的跟踪能力和资源节约情况。

仿真结果：保证定理1中不等式成立的LMI优化结果为γmin=96，将σ=γ-1=0.010 4代入触发机制式(12)，并与周期采样(采样周期T=0.001 s)控制方法进行仿真对比。图3给出的是系统采样事件触发方法和周期采样方法跟踪阶跃信号的输出演化曲线，从中可看出两种方法获得的跟踪曲线基本重合，说明ET方法基本能够取得和TT方法一致的跟踪效果。图4给出的是ET方法的采样间隔散点图，可看出ET方法的最大采样间隔接近2.6 s，除初始4 s时间段内，其他时刻(跟踪进入稳态后)采样间隔约在1～1.5 s内，这说明ET方法可获得较大采样间隔。实际计算ET方法平均采样间隔为0.183 5 s，较周期采样方法采样间隔扩大约180倍，但二者获得的跟踪效果接近一致。这说明针对这一算例ET方法可节约99.4%的通信资源，需要注意的是这仅为直观的定性仿真，具体性能还需通过定量角度对比。

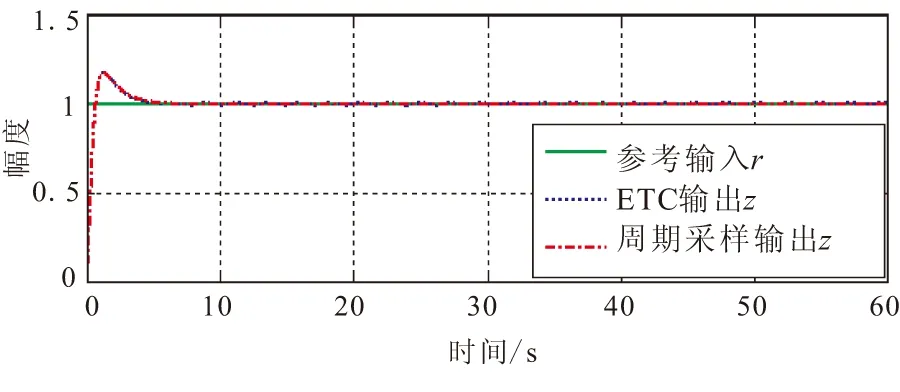
图3　ET与周期采样方法的跟踪曲线

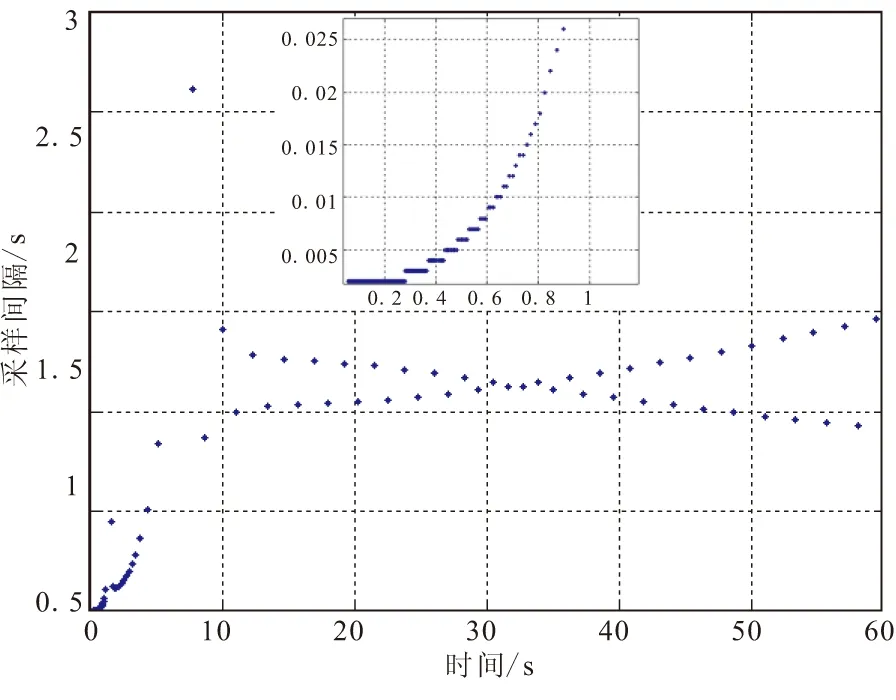
图4　ETC事件触发间隔散点图

4.2跟踪性能验证

仿真目的是研究ET方法对斜坡信号、正弦信号和方波信号的跟踪能力，并从定量的角度对比ET方法与周期采样方法的跟踪性能。

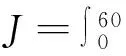
仿真结果：ET方法跟踪斜坡信号，正弦信号和方波信号的输出曲线及触发间隔散点图如图5所示。从图5中可看出，ET方法可有效跟踪各种信号。表1给出的是2种方法对不同信号的跟踪情况定量仿真结果。从表1中可看出，当输入信号为斜坡信号时，ET方法在σ=0.002时取得的跟踪性能等同于T=0.001 s时的周期采样跟踪性能，但平均采样间隔Tmean=0.011 2 s,可实现节约通信资源91%；当输入正弦信号，ET方法在σ=0.010 4时取得的跟踪性能优于T=0.001 s时的周期采样跟踪性能，但平均采样间隔Tmean=0.008 0 s,可实现节约通信资源77.5%；当输入方波信号，ET方法在σ=0.010 4时取得的跟踪性能基本相当于T=0.001 s时的周期采样跟踪性能，但平均采样间隔Tmean=0.013 0 s，可实现节约通信资源92.3%。

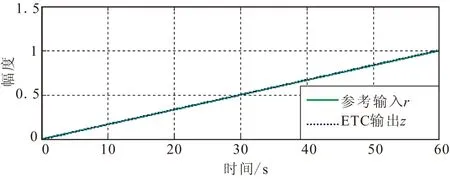
(a)跟踪斜坡输入的输出曲线

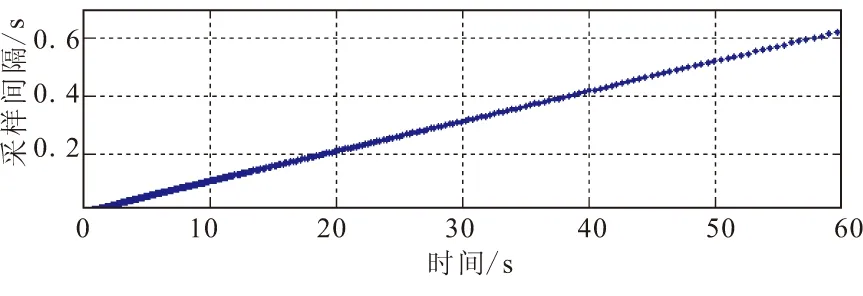
(b)跟踪斜坡输入的事件触发间隔散点图

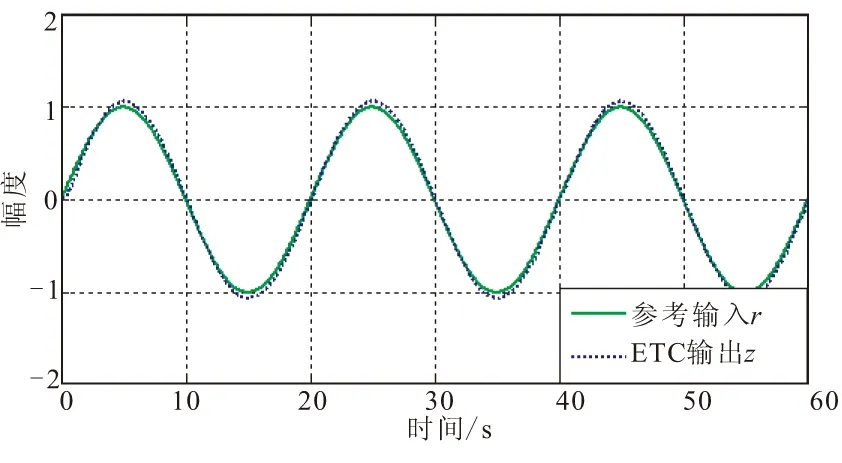
(c)跟踪正弦输入的输出曲线

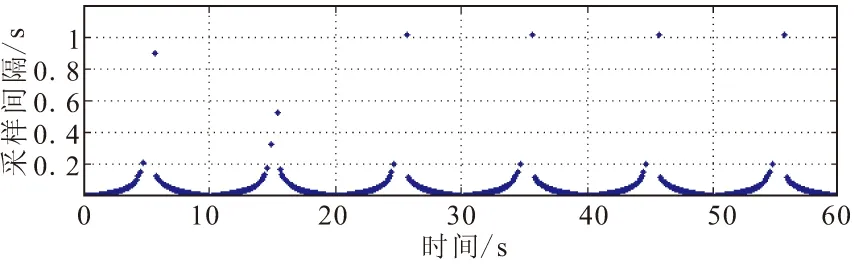
(d)跟踪正弦输入的事件触发间隔散点图

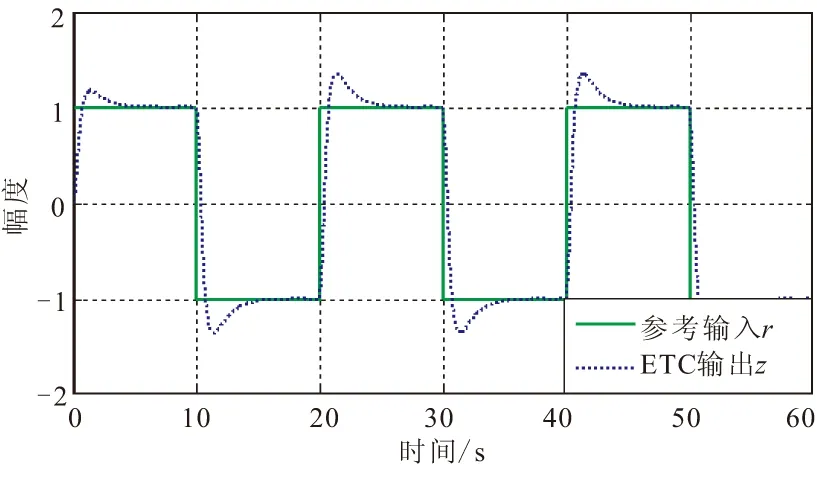
(e)跟踪方波输入的输出曲线

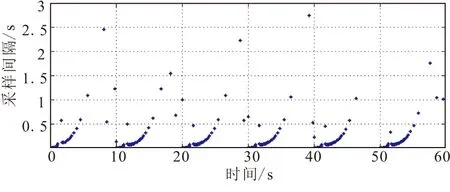
(f)跟踪方波输入的事件触发间隔散点图

采样方法斜坡信号正弦信号JTmean/sJTmean/s周期采样T=0.0015.6×10-50.0010.1460.001ET方法σ=0.01044.74×10-40.07050.1440.0080ET方法σ=0.0051.3×10-40.02610.1430.0043ET方法σ=0.0025.5×10-50.01120.1400.0021采样方法方波信号JJ1Tmean/s周期采样T=0.0016.01757.2×10-40.001ET方法σ=0.01046.01016.15×10-40.0130ET方法σ=0.0056.00976.12×10-40.0075ET方法σ=0.0026.00016.10×10-40.0040

4.3结果的保守性

仿真目的是考查定理2的保守性，仿真中以正弦信号为例，通过设置参数σ变大，观察ET方法是否还具备跟踪能力。仿真结果如表2所示，结果表明，在σ=0.2的情况下，系统还具备跟踪能力。由此可见，依据定理2设计出的触发机制参数存在着一定的保守性，系统实际的稳定门限要更大一些。此外，随着参数σ的变大，跟踪性能下降明显。

表2　参数σ对跟踪性能的影响

5　结论

(1)推力矢量控制中的伺服机构控制实为跟踪控制问题，采用基于跟踪控制输出偏差设计的ETSC系统，可采用受扰系统理论，实现系统的分析和触发机制的设计。

(2)在跟踪阶跃信号时，ETSC能够保持与文献[11]相同的跟踪响应时间情况下，节约99%的通信资源；通过对斜坡信号，正弦信号和方波信号跟踪仿真说明，ETSC方法对于任意参考输入信号的跟踪，相比周期采样方法，可实现77.5%以上的通信资源节约。

(3)实际工程应用时，依据本文方法设计出的触发机制参数偏保守，可根据工程需要适当调大，从而实现更多的通信资源节约，但这会导致跟踪精度的下降。

[1]包为民.航天飞行器控制技术研究现状与发展趋势[J].自动化学报,2013,39(6):697-702.

[2]陈宗基,张汝麟,张平,等.飞行器控制面临的机遇与挑战.自动化学报,2013,39(6):703-710.

[3]Arzen K E.A simple event-based PID controller[C]//Proceedings of IFAC World Congress,Beijing,1999,(18):423- 428.

[4]Lunze J and Lehmann D.A state-feedback approach to event-based control[J].Automatica,2010,46(1):211-215.

[5]WPMH Heemels,Sandee J H,PPJ Van Den Bosch.Analysis of event-driven controllers for linear systems[J].International Journal of Control,2008,81(4):571-590.

[6]Tabuada P.Event-triggered real-time scheduling of stabilizing control tasks[J].IEEE Transactions on Automatic Control,2007,52(9):1680-1685.

[7]Lehmann D,Lunze J.Event-based output-feedback control[C]// IEEE 19th Mediterranean Conference on Control & Automation (MED).Corfu,2011:982-987.

[8]Henningsson T,Johannesson E,Cervin A.Sporadic event-based control of first-order linear stochastic systems[J].Automatica,2008,44(11):2890-2895.

[9]Donkers MCF,WPMH Heemels.Output-based event-triggered control with guaranteedL∞-gain and improved and decentralized event-triggering[J].IEEE Transactions on Automatic Control,2012,57 (6):1362-1376.

[10]Yu H,Antsaklis P J.Event-triggered output feedback control for networked control systems using passivity:AchievingL2stability in the presence of communication delays and signal quantization[J].Automatica,2013,49(1):30-38.

[11]陆豪,李运华,田胜利,等.驱动大惯量低刚度负载的推力矢量控制电动伺服机构的μ综合鲁棒控制[J].机械工程学报,201147(2):180-188

[12]Nesic D,Teel A R.Input-output stability properties of networked control systems[J].IEEE Transactions on Automatic Control,2004,49 (10):1650-1667.

[13]Qiu Jian-bin,Feng Gang,Gao Hui-jun.Fuzzy-model-based piecewiseH∞ static-output-feedback controller design for networked nonlinear systems[J].IEEE Transactions on Fuzzy Systems.2010,18(5):919-934

(编辑：薛永利)

Design of event-triggered servo control systems for thrust vector control

LI Guo-liang1,ZHANG He-xin1,HU Xiao-xiang1,SUN Peng1,ZHOU Xin1

(Department of Automation,Second Artillery Engineering College,Xi'an710025,China)

An event-triggered servo control (ETSC) method, which can solve the communication resources constrained problem in design of a digital & flat control and guidance system for spacecraft,was proposed.Compared with traditional periodical data sampling control method,data sampling and transmission are related to the deviation of tracking output in the ETSC system,so there will be no sampling and transmission when the deviation is in an allowable range.By considering the deviation of tracking output as a disturbance,ETSC system can be modeled as a input-output perturbed systems.Based on stability theory of perturbed systems,stability condition of ETSC system is deduced in the form of linear matrix inequalities (LMIs),which is convenient to the event-triggering scheme design.Simulation results show that,compared with the periodical data sampling control method,ETSC method can save more than 77.5 % of the communication resources.

event-triggered control;servo control;system design;event-triggering scheme design

2015-12-13；

2016-01-14。

国家自然科学青年基金项目(61304001，61304239)。

李国梁(1981—)男，博士生，从事基于事件触发的网络化控制系统分析与设计的研究工作。E-mail：lison_1981@163.com

张合新(1965—)，教授/博导，主要从事飞行器自动化测控方面的研究。

V448

A

1006-2793(2016)02-0269-06

10.7673/j.issn.1006-2793.2016.02.021