二项式定理活用例析
安徽省安庆一中 付贤民
二项式定理活用例析
安徽省安庆一中 付贤民

二项式定理是高中数学中的重点知识,其中蕴含着丰富的数学思想方法与技巧,能在解决诸多问题中得以运用。下面分类举例分析。
一、求指定项的系数
分析根据通项公式,令x的指数为2即可求出系数。要注意项的系数与二项式系数的区别。
二、求指定项
A.-20 B.20 C.-15 D.15
分析本题将分段函数与二项式定理结合起来,必须先求出f[f(x)]的表达式,在求解的过程中注意分类讨论,再利用通项公式找到常数项。

A.1 B.2 C.3 D.4
分析先根据前三项的系数成等差数列求出n的值,写出展开式的通项公式,要使其为有理项,则x的指数必须为整数。
三、求系数和

分析分别令x=1和x=-1,再整体求解。


四、已知系数(或和),求参数值(或范围)
例5 (2015年全国卷)(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a=____。
分析设出(a+x)(1+x)4的展开式,利用赋值法来求解。
解设(a+x)(1+x)4=a0+a1x+a2x2+a3x3+a4x4+a5x5,
令x=1,则(a+1)×16=a0+a1+a2+a3+a4+a5①;
令x=-1,则0=a0-a1+a2-a3+a4-a5②。
①-②得16(a+1)=2(a1+a3+a5)=64,解得a=3,故填3。
分析先利用二项展开式的通项公式求出a、b间的关系式,再利用重要不等式求解。
令12-3r=3,得r=3。
五、求余数或整除问题
例7 5310被8除的余数是( )。
A.1 B.2 C.3 D.7
分析因53=48+5,利用二项式定理将其展开,则只需考虑510被8除的余数即可。
例8 对任意n∈N*,34n+2+a2n+1能被14整除,则最小的自然数a=。
分析因34n+2+a2n+1=92n+1+a2n+1=(14-5)2n+1+a2n+1,而由(14-5)2n+1的展开式知其前2n+1项都能被14整除,最后一项为-52n+1,即对任意n∈N*,-52n+1+a2n+1能被14整除或等于0。
解根据分析可知最小的自然数a=5。
六、求近似值
例9 (1.05)6的计算结果精确到0.01的近似值是( )。
A.1.23 B.1.24 C.1.33 D.1.34
分析将1.05改写成1+0.05,利用二项式定理展开,根据要求去掉后面比较小的项即可求出近似值。

七、创新题
例10 观察下列各式:
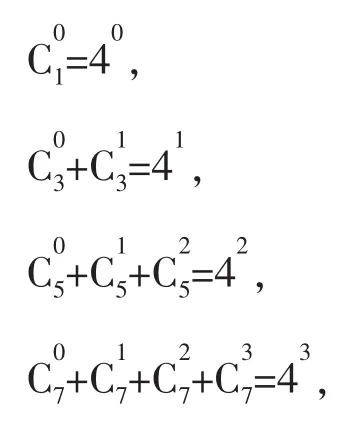
照此规律,当n∈N*时,

分析观察等式左右两边的特点,不难发现答案为4n-1。对于这样的创新题,要求同学们具有较强的观察能力和归纳能力。解题的关键在于抓住题目给出的结构特征,从适当的角度挖掘出其内部规律。


故填4n-1。
例11 当x∈R,|x|<1时,有如下表达式:

请根据以上材料所蕴含的数学思想方法,计算:
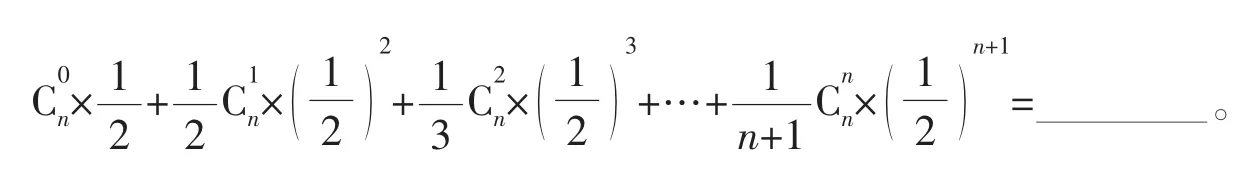
分析本题将导数、定积分、二项式定理巧妙地结合起来,要求同学们具有较好的理解能力、分析问题和解决问题的能力。


