光电设备载车悬架系统匹配设计与动态测试

赵勇志，曹玉岩，王志臣

（中国科学院长春光学精密机械与物理研究所，长春　130033）

光电设备载车悬架系统匹配设计与动态测试

赵勇志，曹玉岩，王志臣

（中国科学院长春光学精密机械与物理研究所，长春130033）

为了提高光电设备载车行驶的平顺性和设备安全性，研究了载车悬架系统匹配设计方法。首先，在忽略油气/空气弹簧非线性特性条件下，推导了载车被动悬架系统的刚体动力学模型，得到了车身位移与路面输入之间的传递函数。其次，基于统计特性给出了随机路面的频域模型，并利用谐波叠加法对路面模型进行重构，进而得到路面时域模型用于仿真分析。然后，基于车体位移传递函数和路面输入模型，推导了车体均方根加速度的表达式，并采用定量分析方法对悬架系统参数进行匹配设计。最后，对悬架系统进行数值仿真，并对整个系统进行动态测试。理论仿真与实测结果基本一致，且均方根加速度值均能满足小于0.2g的指标要求，表明推导的动力学模型能够准确描述载车动力学性能。

光电设备；载车；悬架系统；随机路面；均方根加速度

随着光电测量技术的飞速发展，对设备提出的测量需求与任务越来越多，同时要求不断提高，固定站的光电测量设备已经不能满足实际需求。为了摆脱固定站的条件限制，拓宽设备测量范围，以使其便于对灵活目标如机动导弹等的弹道测量，未来光电测量设备趋于大型化、机动化。在车载光电设备中，载车不仅为设备的运输平台，而且为设备工作平台，与传统仅实现车载运输的落地测量相比，省去了烦琐的就位过程，实现了机动式不落地测量［1，2］。

光电设备属于高精度系统，载车是承载设备重量的主体，在运输过程中过大的振动和冲击将对设备元件尤其是光学元件等产生不利影响，为了保证光电设备安全及功能，要求载车平台运输过程中具有良好的减震性能，同时具有足够的刚度，以保证设备在定位后不会产生过大位置偏差。载车悬架系统是影响整个系统动态性能的主要因素［3，4］。已有研究表明悬架系统建模是非常复杂的问题，尤其是考虑了弹簧及阻尼系统的非线性特性情况［5-12］，而行驶中的载车对光电设备冲击的大小主要取决于油气悬架和空气悬架的刚度及阻尼特性。为此有必要对载车悬架系统进行深入研究，通过合理的匹配设计，使结构的动态性能满足运输光电设备的要求。

本文首先推导了载车被动悬架系统的刚体动力学模型，得到了车体加速度与路面输入之间的传递函数。其次，基于统计特性给出了随机路面的频域和时域模型，并基于车体位移传递函数推导了均方根加速度的表达式，并采用定量分析方法进行悬架系统参数进行匹配设计。最后，对悬架系统进行数值仿真，并对整个系统进行动态测试。

1　悬架系统匹配设计

1.1光电设备载车结构概述

光电设备载车总体结构如图1所示，由牵引车和半挂车组成，其中牵引车主动轮采用双轮空气悬架系统，半挂车从动轮采用双轮油气悬架系统。悬架组件如图2所示，包括轮胎、油气弹簧及摆臂等，其中油气/空气弹簧是载车结构减震的主要元件。

图1　光电设备载车结构

图2　悬架组件

1.21/4悬架系统动力学建模

车身垂直加速度是评价悬架系统减振特性的重要参数，为此需要建立路面激励与车身垂直加速度的传递函数，进而优化系统性能及参数。为了简化系统模型，作如下假设：i）仅考虑载车垂直方向的振动；ii）轮胎始终保持与地面接触；iii）忽略非线性因素的影响。

载车悬架系统动力学模型如图3所示，车轮简化为弹簧，悬架系统等效为两个弹簧及一个阻尼器的组合。在实际中，悬架油气或空气弹簧的刚度和阻尼具有较强的非线性特性。为了简化，在此将弹簧及阻尼器以线性模型表示。如图3中，M为悬架所承担的车体及载荷质量，mj为轮胎j的质量，Ksj及Ktj分别为油气/空气弹簧系统j的刚度及轮胎j的等效刚度，Csj为悬架阻尼，下标表示车轮1和2，x，xwj及xrj分别为车身位移、轮胎j的位移及路面对轮胎j的激励位移。以f1j表示路面对轮胎j的作用力，f2j表示车体及载荷对油气弹簧/空气系统j的作用力，j=1，2。

图3　被动悬架动力学模型

在时域内，载车悬架系统动力学模型可表达为

对式（1）～（4）进行拉氏变换得

式（5）～（8）相互耦合，为了简化，假设悬架及载荷系统对油气/空气弹簧系统1和2的载荷一致，即

轮胎1和2及油气/空气弹簧系统1和2的型号完全一致，即

轮胎1和2间的距离与车体跨度相比非常小，近似地面对两轮胎的激励位移一致，即

将式（14）代入式（2）得

将式（9）代入式（8）得

由式（5）～（8）可得载车悬架系统的位移传递函数Hd（s）为

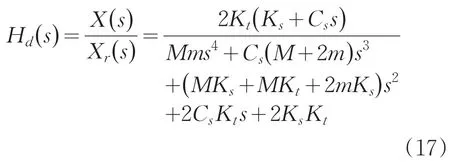
根据位移传递函数Hd（s）即式（18）和拉氏变换的性质，可得悬架系统的加速度传递函数Ha（s）为

1.3随机路面数值建模

路面不平度是影响载车运动平顺性的重要影响因素，是载车振动的主要激励源，为了准确估计光电设备载车运输过程中的振动响应，需对路面不平度进行时域和频域内的准确模拟。假设在一段足够长的直线内，载车行使的路面整体水平，其垂直路面方向上的不平度可认为是一个空间平稳随机过程。路面不平度通常采用功率谱密度函数来表达，即［13］：

式中，n（m-1）为空间频率；n0=0.1m-1为参考空间频率；Gd（n0）表示在空间频率n0下路面的功率谱密度值，各等级路面的Gd（n0）如表1所示；p为频率指数，通常p=2。

表1　各等级路面Gd（n0）数值

空间频率n与时间频率f的关系为

式中，v为车速。

由式（20）和（21）可得时域功率谱Gd（f）为

路面不平度的常用模拟方法主要有随机谐波叠加法［14］、伪白噪声法［15］和随机序列法等，其中随机谐波叠加法简单易实现而且模拟较为准确，其基本原理为将路面的不平度表示为一系列具有随机相位的正弦波的叠加。随机谐波叠加法实现过程如下：

假设载车行驶的道路为窄带随机过程，在时域频带f1＜f＜f2内的道路功率谱密度为Gd（）f，利用平稳随机过程的性质，路面不平度的方差为［14］

将区间（f1，f2）分割为若干子区间，以每个子区间中心频率fmid-i（i=1，2，…）处的Gd（fmid-i）值代替整个子区间内的Gd（f）值，则式可近似为

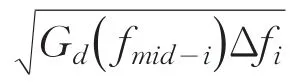
式中，θi在［0，2π］上服从均匀分布。

以C级路面为例，车速为v=30km/h，路面位移输入的时域模型如图4所示。

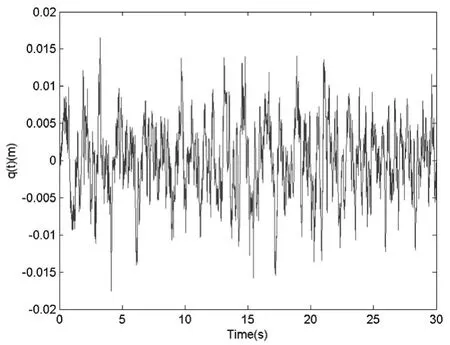
图4　C级路面位移输入时域模型

1.4悬架匹配设计

如图1所示，悬架系统中油气弹簧和空气弹簧的刚度及阻尼特性对载车行驶中的振动特性有重要影响，行驶中载车对光电设备冲击主要取决于系统动态性能，为此需要通过合理的匹配设计，使结构的动态性能满足运输光电设备的要求。

假设载车悬架以上部分及光电设备的重心距离主动轮和从动轮的距离分别为L1和L2，载车及光电设备的总质量为M，根据力平衡和力矩平衡关系可得到空气悬架和油气悬架承担的载荷分别为

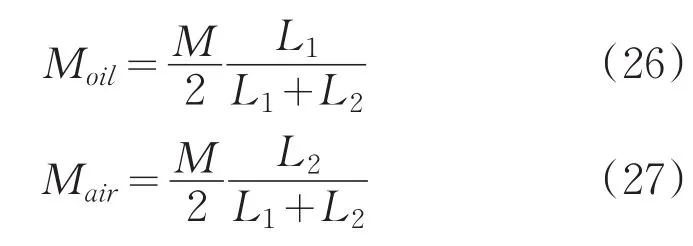
式中，1/2表示悬架以上载荷部分具有对称性。

将式（26）或（27）及（22）代入式（18）中可得加速度输出的功率谱密度为

加速度均方值a¯可表达为

对式（29）求积分得

通过对光电设备的分析，已经得到了在运输过程中，要求载车垂直加速度均方根值小于0.2g，否则将对设备性能造成影响，由于计算过程非常繁琐，在此不再赘述。

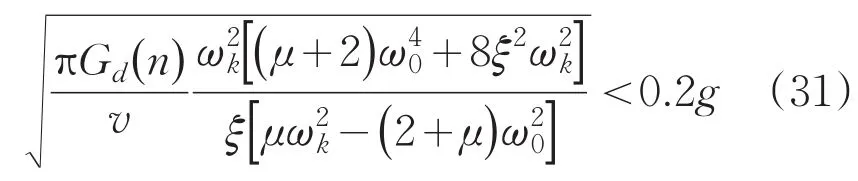
由式（30）可得载车行驶中动态性指标条件为式中，轮胎选定及气压确定后μ，ωk为固定常数，载车及设备质量确定后，悬架载荷为固定常数，ω0及阻尼系数ξ为未知量，需要对其进行匹配设计。

动态性能指标匹配设计条件，即式（31），形式非常复杂，对油气/空气弹簧刚度Ks（或ω0）及阻尼系数ξ进行最优匹配设计需要较复杂的优化算法，在此本文采用了一种定量的分析方法，首先分析载车均方根加速度与阻尼系数及弹簧刚度系数之间的变化关系，进而选择合适的系数作为载车悬架设计参数。载车及光电设备载荷及距离参数如表2所示，轮胎选用12.00-R20中型载重轮胎，每个轮胎当充气压力770kpa时可承载3.52吨，足以满足承载要求，由式（26）和（27）可得到油气和空气弹簧悬架的承载质量分别为10922kg和7078kg。

表2　载车及设备相关参数

以一个悬架为例，分析1/4车体的动态性能，令阻尼系数ξ=0.3，油气及空气弹簧悬架下载车的均方根加速度随刚度系数变化情况如图5和6所示。

图5　油气弹簧刚度与均方根加速度关系

图6　空气弹簧刚度与均方根加速度关系

从图5和6中可发现，载车的均方根加速度值随着弹簧刚度的增大而增大，即弹簧刚度越大，载车对光电设备的冲击越大。此外，弹簧刚度决定了载车的静态挠度及谐振，为了使结构尽可能稳定又不至于影响结构性能，应在满足均方根加速度的前提下尽量提高弹簧刚度。

同样，分析1/4车体的动态性能，令油气弹簧刚度系数为1.22×106N/m及空气弹簧刚度系数为0.775×106N/m，载车的均方根加速度随阻尼系数变化情况如图7和8所示。

图7　油气弹簧刚度与均方根加速度关系

图8　空气弹簧刚度与均方根加速度关系

从图7和8中可发现，均方根加速度值随着阻尼系数的增大而减小。通过对图5～8的分析比较及反复核算，最终确定油气弹簧及空气弹簧的刚度系数分别为Ks=1.22×106N/m和Kt=0.775×106N/m，阻尼系数均为0.32。

2　数值仿真与动态测试

2.1数值仿真

考虑如图1所示的载车结构，首先以随机谐波叠加法产生的随机路面模型作为输入条件（如图4所示），分别对油气及空气弹簧悬架下1/4车体的动态性能进行数值仿真，相关参数如表2所示。油气及空气悬架下，载车振动加速度响应如图9和10所示，加速响应的均方根值分别为0.177g和0.178g，满足了均方根加速度小于0.2g的要求。

图9　油气弹簧悬架加速度响应

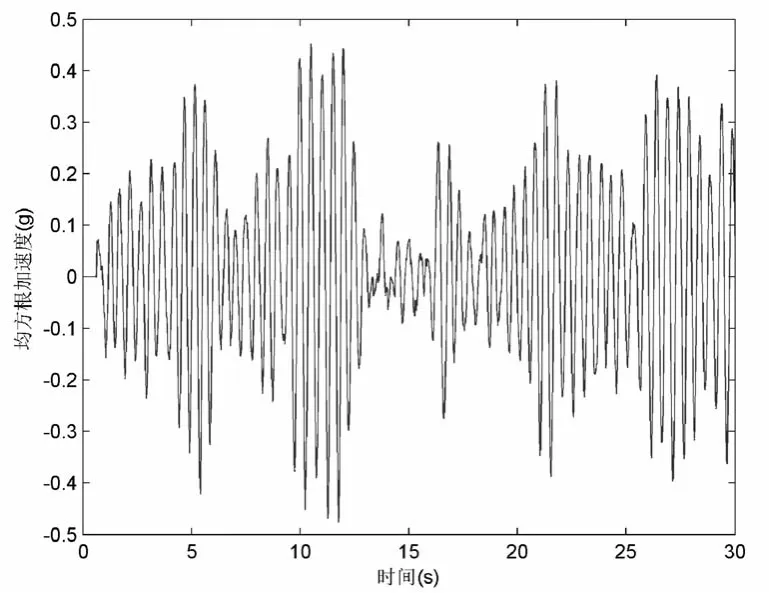
图10　空气弹簧悬架加速度响应

2.2动态测试

对载车及设备整体结构进行跑车测试，载车以30km/h的速度在C级公路上行驶，采用加速度计测试垂直加速的变化情况。在载车两端即空气及油气悬架位置处各放置一个加速度计，如图11和12所示，加速度计测试结果如图13所示。

图11　传感器固定位置

图12　载车及设备动态测试

图13　振动加速度测试曲线

根据加速度计的测试数据，经过计算处理得到加速度均方根及均值如表3所示，两加速度计测量的加速度均值接近于零，均方根值均小于0.2g，满足运输光电设备的要求。

表3　加速度计测试

3　结论

研究了光电设备载车悬架系统匹配设计问题，推导了载车被动悬架系统的刚体动力学模型，基于随机路面的频域和时域模型，推导了车体竖向均方根加速度的表达式，并采用定量分析方法进行悬架系统参数进行匹配设计，对悬架系统进行数值仿真和系统动态测试。

结果表明，理论仿真与实测均方根加速度值基本一致，且均方根加速度值均能满足小于0.2g的指标要求，表明推导的动力学模型能够准确描述载车动力学性能，为光电设备载车悬架系统设计提供理论依据。

［1］Albertine JR.History of Navy HEL technology developmentandsystemstesting［J］.LaserAnd Beam Control Technologies.2002；4632：32-37.

［2］Ruffatto D，Brown D，Pohle R，Reiley M，Haddock D.Stabilized high-accuracy optical tracking system（SHOTS）［J］.Proceedings of SPIE.2001；4365：10-18.

［3］Turkay S，Akcay H.Aspects of achievable performance for quarter-car active suspensions［J］.Journal of Sound and Vibration.2008；311：440-460.

［4］Gordon TJ.nonlinear optimal-control of a semiactive vehicle suspension system［J］.Chaos Solitons &Fractals.1995，5：1603-1617.

［5］尹万建，韩鹰，杨绍普.空气弹簧悬架系统在强迫振动下的动力学分析［J］.中国公路学报，2006，19（03）：117-121.

［6］尹万建，杨绍普，申永军，等.空气弹簧悬架的振动模型和刚度特性研究［J］.北京交通大学学报，2006，30（01）：71-74.

［7］陈燎，周孔亢，李仲兴.空气弹簧动态特性拟合及空气悬架变刚度计算分析［J］.机械工程学报，2010，46（04）：93-98.

［8］袁春元，周孔亢，吴琳琪，等.车用空气弹簧有限元分析方法［J］.机械工程学报，2009，45（06）：262-266.

［9］Eski I，Yidirim S.Vibration control of vehicle active suspension system using a new robust neural networkcontrolsystem［J］.SimulationModelling Practice and Theory，2009，17：778-793.

［10］李杰，秦玉英，赵旗.汽车随机振动的建模与仿真［J］.吉林大学学报：工学版，2010，40（02）：316-319.

［11］周晓兵，姜玉波，周永福，等.基于平顺性的汽车悬架主要参数设计方法［J］.长春理工大学学报：自然科学版，2014，37（02）：46-48.

［12］陈广秋，孙蕙莲.汽车悬架性能测试系统的研究与设计［J］.长春理工大学学报：自然科学版，2009，32（03）：388-392.

［13］段虎明，石峰，谢飞，等.路面不平度研究综述［J］.振动与冲击，2009，28（09）：95-101，216.

［14］常志权，罗虹，褚志刚，等.谐波叠加路面输入模型的建立及数字模拟［J］.重庆大学学报：自然科学版，2004，27（12）：5-8.

［15］张永林，钟毅芳.汽车道路双轮辙多点随机激励建模与仿真研究［J］.系统仿真学报，2004，16（06）：1147-1149，1154.

Matching Design and Dynamic Test for the Suspension System of Vehicle Optical-electric Equipment

ZHAO Yongzhi，CAO Yuyan，WANG Zhichen
（Changchun Institute of Optics，Fine Mechanics and Physics，Chinese academy of sciences，Changchun 130033）

In order to improve the ride comfort and security of vehicle，the matching design method for the suspension system of vehicle is investigated.Firstly，the rigid body dynamic model of the suspension system is derived based on the assumption that the nonlinearity of oil-gas spring or air spring is omitted，and then the transfer function between the body acceleration and the road input is obtained.Secondly，the frequency domain model of stochastic roads is introduced based on the statistics property and is reconstructed using harmony superposition method，and then the time domain model of that road is obtained and used to simulation.Then，based on the transfer function and the model of stochastic road，the expression of mean square root acceleration of body is derived and the matching design of the parameters of suspension system is presented using quantitative methods.Finally，the numerical simulation of the suspension system is given and the dynamical test is processed.The results between the simulation and test have a good consistence，and the mean square root acceleration of body is less than the criteria constrain that＜0.2g，which indicate that the derived model can be used to precisely depict the dynamical property of vehicle.

optical-electric equipment；vehicle；suspension system；stochastic roads；mean square root acceleration

TP13

A

1672-9870（2016）04-0097-06

2016-03-16

国家自然科学基金（11403023）

赵勇志（1979-），男，博士，副研究员，E-mail：13504314756@126.com