纳米精度二维工作台测量镜的面形误差在线检测
刘兆武,李文昊,王敬开,姜 珊,宋 莹,潘明忠,巴音贺希格*
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 101408;3.北京航空航天大学,北京 100191)
纳米精度二维工作台测量镜的面形误差在线检测
刘兆武1,2,李文昊1,王敬开3,姜珊1,宋莹1,潘明忠1,巴音贺希格1*
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 101408;3.北京航空航天大学,北京 100191)
针对二维工作台测量镜本身的面形误差以及装调等因素引起面形变化对二维工作台定位精度的影响,提出了一种用于纳米精度二维工作台测量镜面形误差的在线检测方法。利用两路激光干涉仪检测面形微分数据的基本原理,分析了零点误差和积分累计误差对测量镜面形误差检测的影响并提出了改进方法。利用三路激光干涉仪组成两组不等跨度的检测机构,得到两组工作台测量镜面形的原始数据,通过这两组数据之间的关系修正跨度间的面形细节误差,得到了精确的测量镜面形误差量。对此方法进行了理论推导、仿真计算和实验验证,并将结果与Zygo干涉仪测量得到的离线检测结果进行了对比,结果显示其差异在±10 nm之间,且趋势有较好的一致性。 得到的结果验证了提出的方法可正确测量和真实地还原测量镜的面形误差。
激光干涉仪;纳米二维工作台;测量镜;面形误差;在线检测
1 引 言
二维工作台在精密工程领域的应用越来越广泛[1-3]。目前,纳米精度二维工作台通常采用双频激光干涉仪定位系统[4-6]。在工作台运动过程中,参考镜静止不动,测量镜随工作台运动,由多普勒原理计算出测量镜与参考镜之间的相对位移,从而得到工作台的精确位置。在测量镜装调过程中,测量镜可能产生面形形变,而当工作台沿平行于测量镜镜面的方向运动时,测量镜的面形误差不可避免地会引入到工作台测量中[7],因此必须对工作台测量镜的面形误差进行精密的在线检测。
20世纪60年代,Schulz和Schwider[8]等提出的三面互检法得到广泛应用,在此后的半个世纪里,三面互检法不断进步[9-11],其理论逐渐成熟,目前能够实现RMS值为λ/10 000[12]以上的检测精度,但是检测设备昂贵并且复杂。Schulz[13-14]等提出可追踪多传感器检测法,通过传感器沿被测方向扫描的方式检测大口径高精度平面面形,但是装调可能引起额外的面形变化,无法准确反映工作台工作过程中的镜面面形。Saburo Kamiya[15]提出离线检测与在线检测相结合的方法,以工作状态下的面形获得离散曲线作为在线状态基准,将离线测得的连续面形偏离值附加到在线状态基准上获得测量镜工作状态下的最终面形。这种方法在线检测面形时的采样数据点少,忽略了测量镜安装前后面形的高频变化,不能精确地表示测量镜在工作状态下的面形。何乐[16]等采用多序列法测量工件台的位置和旋转量,通过样条插值与最小二乘原理平滑连接所有测量序列,并计算出精确的测量镜面形。该方法弥补了Kamiya的不足,但是在测量过程中工作台要具有旋转功能,对工作台的结构和控制要求较高。Montoya[17]等提出由采样数据解析出测量镜不平度的方法,然而受到干涉仪检测系统的约束,建立稳定的逆传递函数比较困难,同时来自工件台自身非正交性和基底不平度的影响也难以消除,在长期的运作中稳定性较差。
本文提出了一种纳米精度工作台测量镜面形检测方法,以不等跨度的两组检测机构获取两组测量镜的面形数据,利用两组数据之间的关系修正面形细节误差,从而得到精确的测量镜面形误差。该方法简单,并具有较高的精度和稳定性。
2 测量镜面形检测原理
2.1基本原理
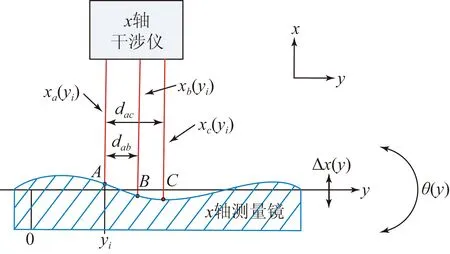
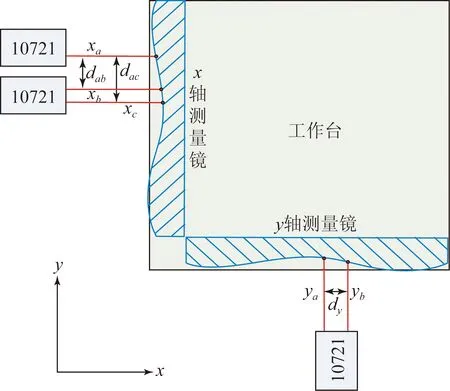
图1为工作台位移测量系统示意图,其中xa,xb为x轴干涉仪两组测量光束的测量结果,ya,yb为y轴干涉仪两组测量光束的测量结果,dx,dy分别为x轴干涉仪和y轴干涉仪两组测量光束的中心间距,则工作台的实际位置(x,y)为:
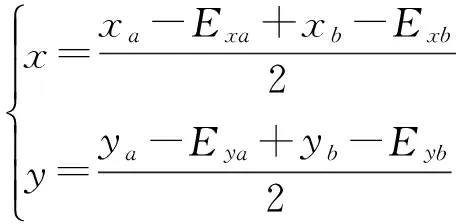
(1)
其中:Exτ为x轴测量镜的面形误差,Eyτ为y轴测量镜的面形误差,τ=a或b。由于工作台为刚体,x轴测量镜上的工作台偏航信息与y轴测量镜上的一致。由于工作台在运动过程中的偏航角度较小,其实际偏航角为:
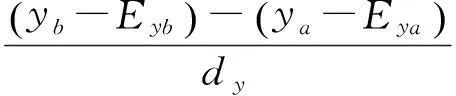
(2)
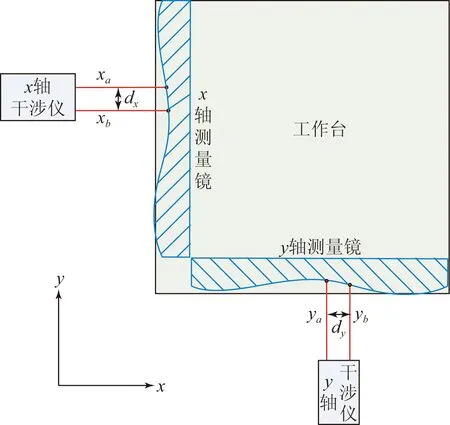
图1 工作台位移测量系统示意图
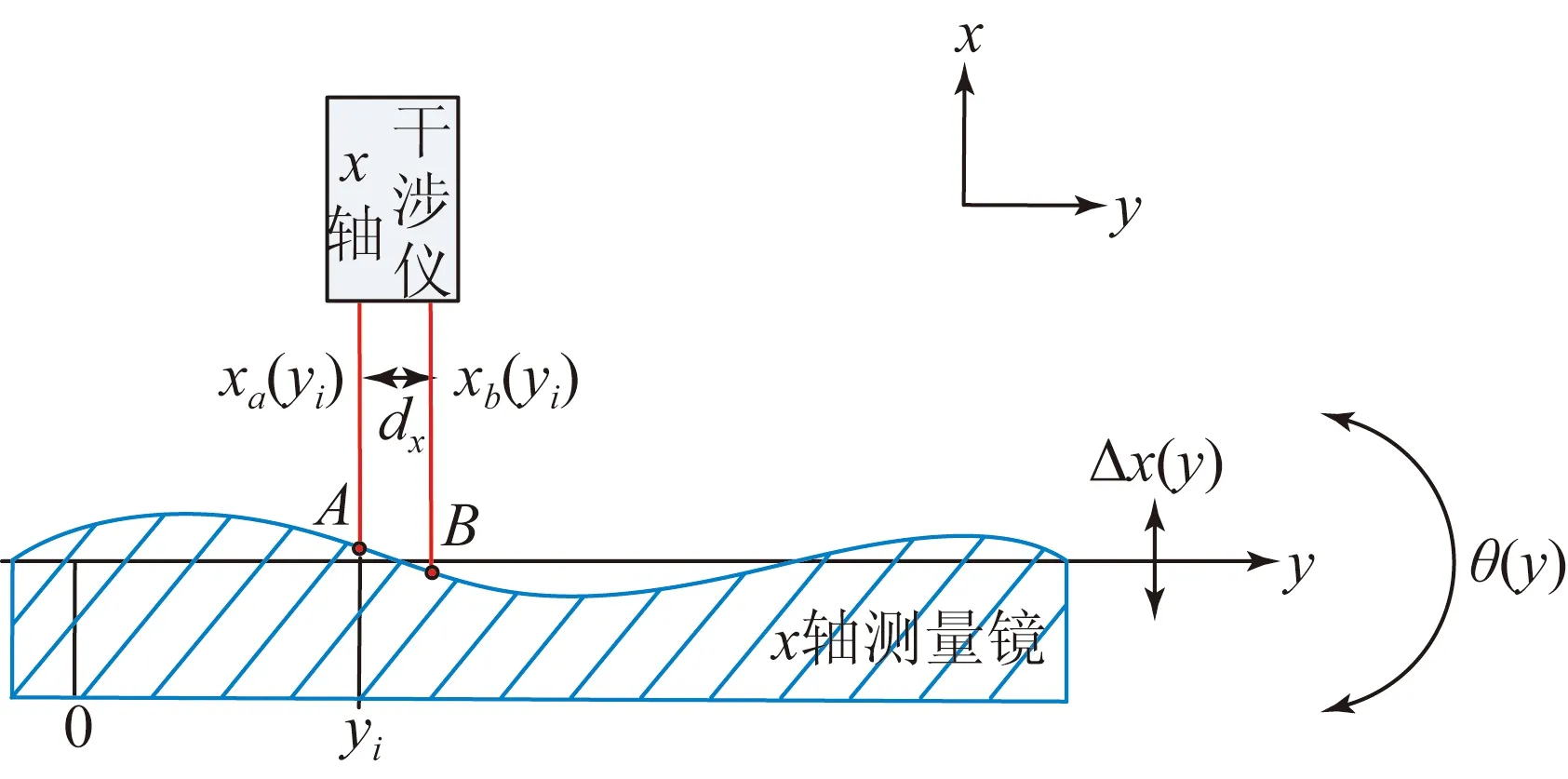
图2 x轴测量镜面形误差检测示意图
如图2所示,以x轴测量镜面形检测为例,测量镜被检测长度为l,工作台沿y轴运动,获取x轴测量镜的面形位移误差Ex(y)。实际工作台在运行过程中存在平移Δ(y)和偏航θ(y),当工作台运行到yi位置时,由式(1)可知,x轴干涉仪两组测量光束检测的测量镜面形误差为:
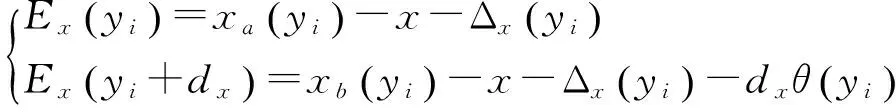
(3)
由于精密加工的测量镜面形曲线变化小、空间频率低,所以面形曲线测量点的导数可以近似为:
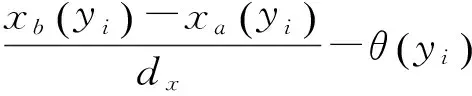
(4)
由式(2)可知:

(5)
在检测x轴测量镜面形时,工作台沿y轴运动,y轴测量镜的测量位置几乎没有变化,并且由于干涉仪测距为相对位移测量,初始测量位置处读数为0,y轴测量镜的面形误差包含在干涉仪读数中,可视为(Eyb(yi)-Eya(yi))/dy=0。则式(4)可写为:
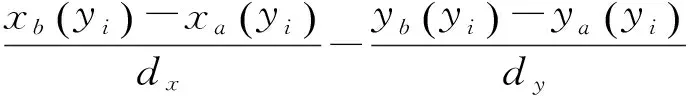
(6)
积分可得x轴测量镜的面形误差为:
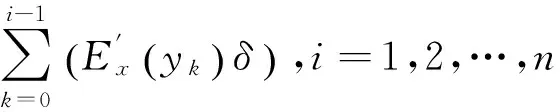
(7)
其中:δ为数据采集周期,n=fix(l/δ)。fix表示向下取整。
2.2误差分析
干涉仪测距为相对位移测量,测量初始位置为干涉仪零点,这意味着干涉仪零点未必是测量面的绝对零点,如图3(a)所示。设x轴两个干涉仪的零点偏差分别为ea,eb,则式(3)改写为:
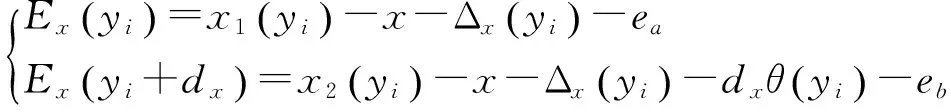
(8)
因此,测量镜的面形误差改写为:
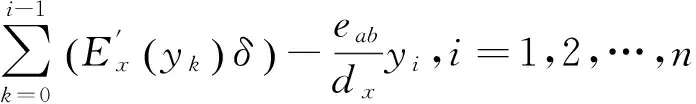
(9)
其中:eab=ea-eb为干涉仪零点差异,可以看出eab将在测量镜面形计算中引入一个线性误差eabyi/dx,这里称之为零点误差,如图3(b)所示。
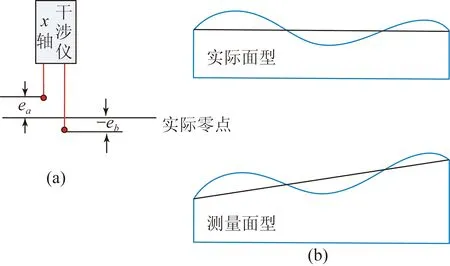
图3 干涉仪的零点偏差及其影响
此外,上述数据处理过程中,采用离散导数进行积分处理,离散采样与实际斜率的差异将引入一个累计误差,称作积分累计误差。积分累计误差是测量光束的中心间距dx与采样周期δ的函数,同时也与被检表面面形误差的空间频率有关。图4所示为在不同采样周期下积分累计误差的变化情况,可以看出,采样周期与测量光束的中心间距越接近,积分累计误差越小。当δ=dx时,积分累计误差为零。
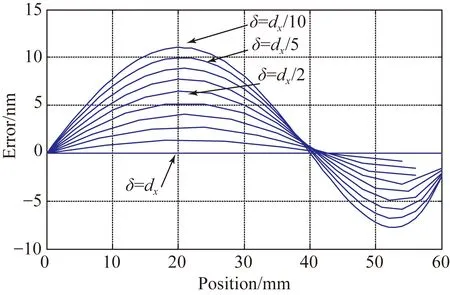
图4 积分累计误差
2.3测量镜面形检测算法改进
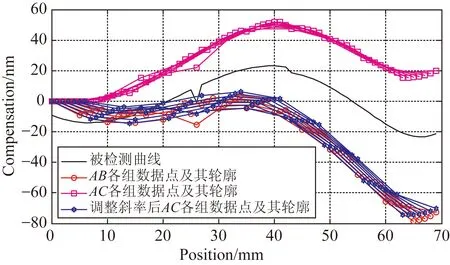
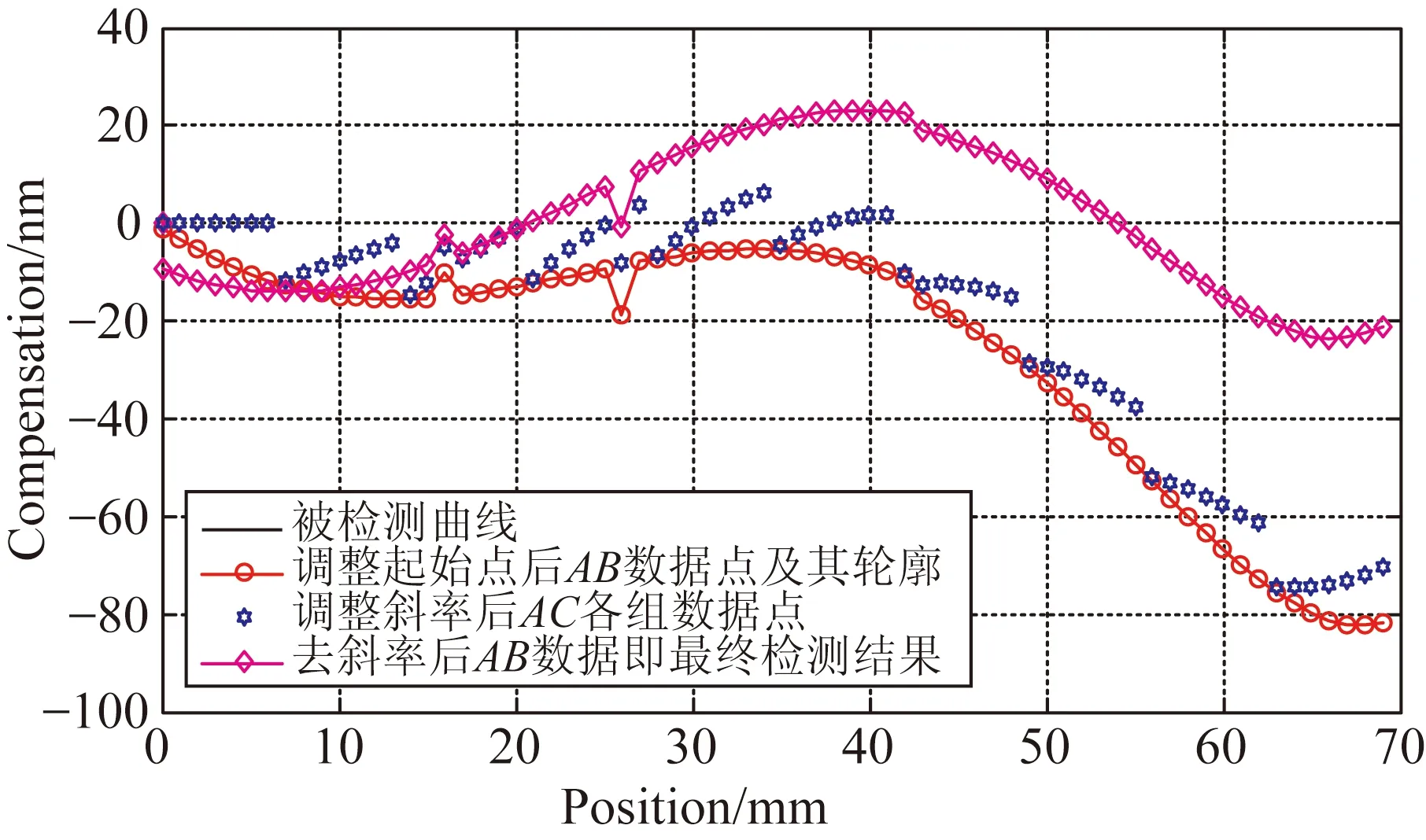
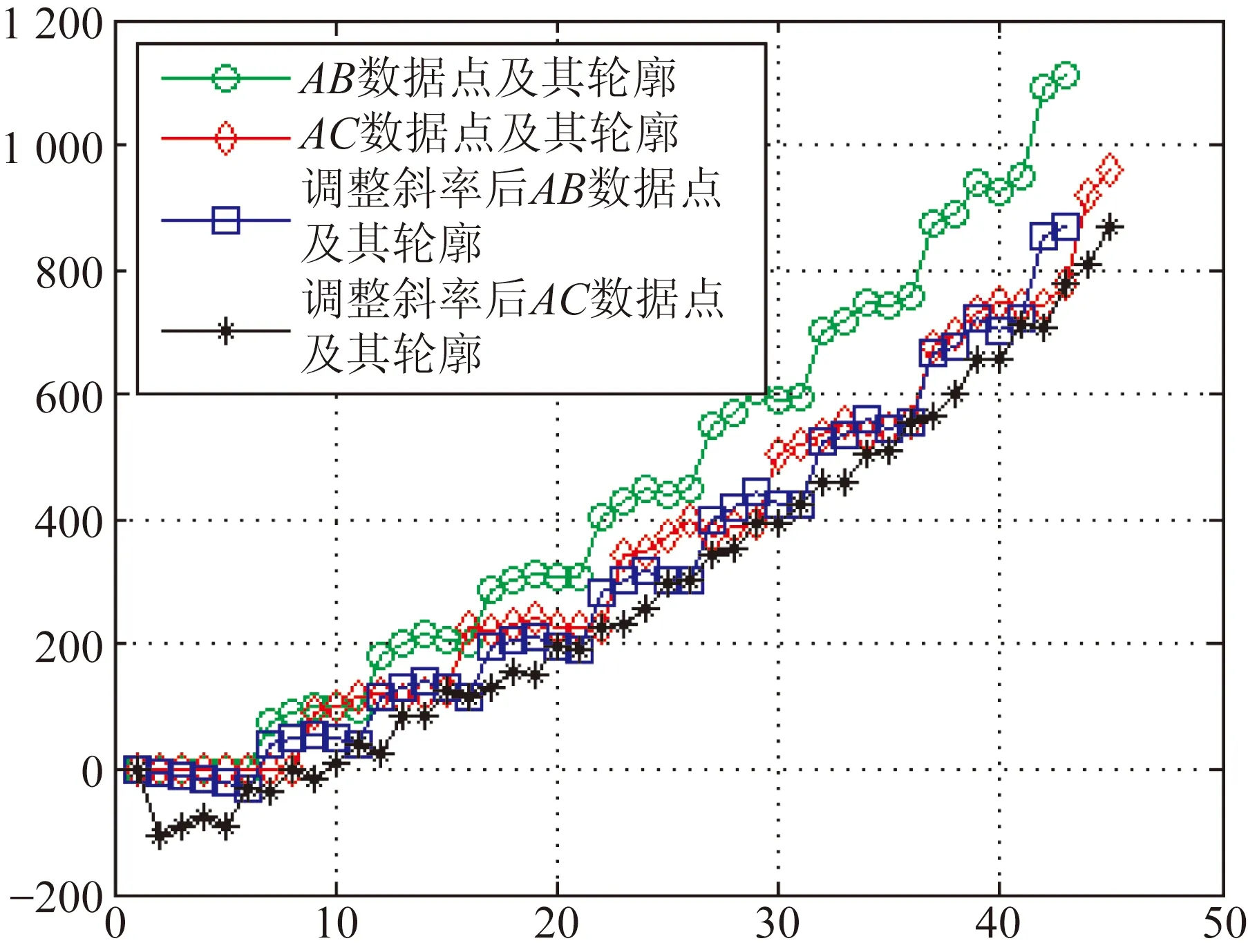
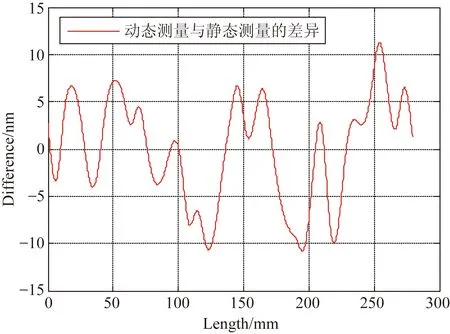
为不引入积分累计误差,又不减少数据测量点,在x轴测量镜C点设置第3个测量计,如图5所示。假设测量镜的被检测长度为l,采样周期为δ,使dab=m1δ,dac=m2δ,m1 (10) 图5 面形检测算法改进示意图 当i=r1m1+t1=r2m2+t2时,测量数据与真实值之间的关系为: (11) 2.3.1改进算法步骤 (1)匹配AB、AC数据斜率 当i=r1m1+t1+m1m2=r2m2+t2+m1m2时,式(11)变化为: (12) 由式(12)和式(13)计算AB、AC数据零点的误差差异: (13) 式(13)的意义在于在AB所得的同一组数据中寻找两点,这两点在AC所得的数据中也处于同一组,对比AB、AC中这两点的数据即可计算AB、AC数据的零点误差差异,可知i≥m1m2的所有点均符合要求,这些数据计算的零点误差差异理论上相等,利用这些数据求平均值可以减少零点误差差异的系统误差。将式(13)带入式(11)第二式中得到: (14) (2)利用AB、AC数据之间的关系调整各组数据的起始点 当i=km2时,t2=0,r2=k,r1=km2-t1,式(11)变化为: (15) 由式(15)计算可知: (16) 其中: (17) 式(17)的意义在于在AB各组数据中找到在AC第一组数据中的测量点,因AC第一组数据中的起始值是明确的,通过AB、AC数据之间的关系确定AB各组数据的起始点位置。将式(16)带入式(11)第一式中得到: (18) 对式(18)等号两边进行去斜率处理,得到测量镜面形为: (19) 2.4模拟仿真 为体现改进算法的普遍性,设置被检测函数为一个非周期、有阶跃、有畸变并且无斜率的函数,设: (20) 设置阶跃和畸变点如下: (21) 去斜率,被检测函数为: (22) 被检测曲线如图6所示,被检测面形长度l=70 mm,面形误差约为-20~20 nm。假设空间采样周期δ=1 mm,dab=m1δ=5 mm,dac=m2δ=7 mm,零点差异eab=-5 nm,eac=3 nm。应用式(13)将AC各组数据与AB各组数据进行斜率匹配,结果如图6所示,图中曲线AB与曲线AC有相同的斜率趋势。然后应用式(18),根据AC第一组数据的位置调整AB数据的起始点,结果如图7所示,得到的连续曲线与被测曲线形状相同,但倾角不同。对调整后的AB数据进行去斜率处理得到检测结果,图中可以看出被检测曲线与去斜率后的AB曲线完全重合,从而在理论上证明了本文所论述的方法能够精确还原测量镜面形。 图6 面形检测模拟仿真步骤一 图7 面形检测模拟仿真步骤二 测量镜面形误差在线检测实验系统光路如图8所示。工作台运行在万级洁净间的气浮隔振平台上,检测光路暂无密封装置,被检测测量镜长为300 mm,有效可检测长度为l=279.4 mm。位移测量采用3部Agilent 10721A双轴差分干涉仪,测量分辨率为0.15 nm,x轴位移测量用其中两部干涉仪的3路测量轴,y轴测量用另外一部干涉仪的2路测量轴,剩余1路测量轴闲置不用。空间采样频率δ=6.35 mm,dab=m1δ=31.75 mm,dac=m2δ=44.45 mm。工作台每运行6.35 mm采集1 000 个数据,取平均值作为该点面形数据以减小噪声的影响,每次测量共采集38组数据,AB有43个数据测量点,AC有45个数据测量点。AB、AC数据点及其轮廓如图9所示,将AB各组数据与AC数据进行斜率匹配,根据匹配后AB第一组数据的位置调整AC数据的起始点,最后对调整后的AC数据进行去斜率处理并拟合为平滑曲线,得到的检测结果如图10所示。测量镜的最大误差跨度约为48 nm。图11给出了同样实验条件下10次实验结果的标准差分布,最大标准差为4.143 1 nm。 图8 测量镜面形误差在线检测实验系统的光路布局 图9 实验数据处理结果 图10 双频激光干涉仪的在线检测结果 为验证此方法的正确性,利用Zygo 32英寸平面激光干涉仪对该表面进行离线检测,检测结果如图12所示,测量镜的最大误差跨度约为38 nm。两种方法的对比结果如图13所示,双频激光干涉仪的在线检测结果与Zygo干涉仪的离线检测结果的趋势基本一致,对应检测点的测量差异在±10 nm 之间,这些差异主要是在测量镜装调过程中引起的面形变化。综上可知,该方法确实可以获取工作台测量镜的面形误差。 图12 Zygo干涉仪的离线检测结果 图13 在线与离线检测结果对比 在试验过程中,由于没有严格控制空气扰动,导致工作台运动过程中气浮平台不稳定,而工作台运行速度的波动会使双频激光干涉仪的检测数据存在一定的偏差。受实验条件的限制,该影响需要进一步的实验验证。 本文提出一种纳米精度二维工作台测量镜面形检测方法,首先利用y轴工作台测量镜修正工作台运动的偏摆误差,利用三路双频激光干涉仪组成两组不等跨度的角检测机构,分别获取两组x轴工作台测量镜面形的微分数据;然后以各自的跨度为间隔积分得到两组工作台测量镜面形的原始数据;最后利用这两组数据之间的关系修正跨度间的面形细节误差,得到精确的x轴测量镜的面形误差量。该方法在不减少面形测量数据点的情况下,避开了零点误差和积分累计误差的影响,能够更真实地还原测量镜的面形误差,并且测量镜的有效利用率高,可以检测到镜面边缘的面形。对该方法进行了理论推导、仿真计算以及在线检测,并与Zygo干涉仪的离线检测结果进行了对比。实验结果表明,该方法的测量重复精度优于4.143 1 nm,与采用Zygo干涉仪对该表面的离线检测结果差异在±10 nm之间,且趋势一致,由此验证了该方法用于检测纳米级工作台测量镜面形的可行性。 该方法通过增加数据测量点、改善工作台运动状态和实验条件、以及对测量光路进行严格密封可以进一步提高精度,这将是下一步的工作重点。 [1]崔继文,刘雪明,谭久彬. 超精密级二维工作台的自标定[J]. 光学 精密工程,2012,20(9):1960-1966. CUI J W, LIU X M, TAN J B. Self-calibration for 2-D ultra-precision stage[J].Opt.PrecisionEng., 2012,20(9): 1960-1966.(in Chinese) [2]张昔峰,黄强先,袁钰,等. 具有角度修正功能的大行程二维纳米工作台[J]. 光学 精密工程,2013,21(7):1811-1817. ZHANG X F, HUANG Q X, YUAN Y,etal.. Large stroke 2-DOF nano-positioning stage with angle error correction [J].Opt.PrecisionEng., 2013, 21(7): 1811-1817.(in Chinese) [3]GAO Z Y, HU J C, ZHU Y,etal.. A new 6-degree-of-freedom measurement method of X-Y stages based on additional information [J].PrecisionEngineering, 2013, 37(3): 606-620. [4]GROOT P J D, BADAMI V G.RevelationsintheArtofFringeCounting:TheStateoftheArtinDistanceMeasuringInterferometry[M]. Springer Berlin Heidelberg, 2014; 785-790. [5]高忠华,陈锡侯,彭东林. 时栅角位移传感器在线自标定系统[J]. 光学 精密工程,2015,23(1):93-101. GAO ZH H, CHEN X H, PENG D L.Online self-calibration system for time grating angular displacement sensor [J].Opt.PrecisionEng., 2015, 23(1): 93-101.(in Chinese) [6]糜小涛,于宏柱,于海利,等. 大型衍射光栅刻划机拉杆结构的分析与改进[J]. 光学 精密工程,2015,23(3):745-752. MI X T, YU H ZH, YU H L,etal.. Analysis and improvement of rod structures for large diffraction grating ruling engines [J].Opt.PrecisionEng., 2015, 23(3): 745-752.(in Chinese) [7]ZHAO Y.Ultra-highPrecisionScanningBeamInterferenceLithographyandItsApplication-spatialFrequencyMultiplication[D]. Cambrige:Massachusetts Institute of Technology,2008. [8]SCHULZ G, SCHWIDER J. Precise measurement of planeness [J].Appl.Optics, 1967, 6(6): 1077-1084. [9]KÜCHEL M F. A new approach to solve the three flat problem [J].Optik-InternationalJournalforLightandElectronOptics, 2001, 112(9): 381-391. [10]GRIESMANN U, WANG Q, SOONS J. Three-flat tests including mounting-induced deformations [J].OpticalEngineering, 2007, 46(9): 093601. [11]SU D-Q, TIAN W, MIAO E-L,etal.. Absolute three-flat test in vertical direction with gravity deformation compensation [J].ActaPhotonicaSinica, 2015, 44(11): 1112003. [12]徐洋,唐锋,王向朝,等. 平面面形绝对检验技术测量误差分析[J]. 中国激光,2011,38(10):204-209. XU Y, TANG F,WANG X CH,etal.. Measurement error analysis of absolute flatness test [J].ChineseJournalofLasers, 2011, 38(10): 204-209.(in Chinese) [13]ELSTER C, WEING R I, SCHULZ M. Coupled distance sensor systems for high-accuracy topography measurement: Accounting for scanning stage and systematic sensor errors [J].PrecisionEngineering, 2006, 30(1): 32-38. [14]SCHULZ M, ELSTER C. Traceable multiple sensor system for measuring curved surface profiles with high accuracy and high lateral resolution [J].OpticalEngineering, 2006, 45(6): 060503. [15]KAMIYA S.Methodandapparatusforcorrectinglinearityerrorsofamovingmirrorandstage:UnitedStates, 5790253 [P]. 1998. [16]何乐, 王向朝, 马明英. 一种测量光刻机工件台方镜不平度的新方法[J]. 中国激光,2007,34(4):519-524. HE L, WANG X CH, MA M Y. Non-flatness measurement of wafer stage mirrors in a step-and-scan lithographic tool [J].ChineseJournalofLasers, 2007, 34(4):519-524.(in Chinese) [17]MONTOYA J.TowardNano-accuracyinScanningBeamInterferenceLithography[D]. Cambrige:Massachusetts Institute of Technology 2006. 巴音贺希格(1962-),男,内蒙古鄂尔多斯人,博士,研究员,博士生导师,2004年于中国科学院长春光学精密机械与物理研究所获得博士学位,主要从事光栅理论、光栅制作技术及光谱技术的研究。E-mail:bayin888@sina.com (版权所有未经许可不得转载) Online detection of profile deviation for nano precision 2-D stage mirror LIU Zhao-wu1,2, LI Wen-hao1, WANG Jing-kai3, JIANG Shan1, SONG Ying1, PAN Ming-zhong1,Bayanheshig1* (1.ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China;2.UniversityofChineseAcademyofSciences,Beijing101408,China;3.BeihangUniversity,Beijing100191,China)*Correspondingauthor,E-mail:bayin888@sina.com For the profile deviation of a stage mirror itself and the profile change caused by the alignment of 2D stage position, an online detection method for the profile deviation of a nano precision 2-D stage mirror was presented. The basic principle of detecting profile differential data with two interferometers was proposed. The influences of zero error and integral error on the measurement were analyzed and a method to improve the measuring precision was put forward. Two sets of original data of the mirror profile were obtained by two sets of detectors with different spans composed by three interferometers. Through the relationship between the two sets of data, the detail profile deviation between the spans was modified. The theoretical calculation, simulation and experiments for the proposed method were performed, and obtained results were compared with that of off-line measurement with a Zygo interferometer. The results show that the most difference in test results is between ±10 nm, and the trend has better consistency, which verify that this measuring method could measure the profile deviation of stage mirrors correctly and could restore its surface errors truly. laser interferometer; nano-2D stage; stage mirror; profile deviation; online detection 2016-01-06; 2016-02-06. 国家重大科学仪器设备开发专项资助项目(No.61227901) 1004-924X(2016)09-2134-08 TN247;TH744.3 A 10.3788/OPE.20162409.2134 刘兆武(1987-),男,黑龙江齐齐哈尔人,博士研究生,2006年于哈尔滨工业大学获得学士学位,主要从事全息曝光系统制作和精密位移测量等方面的研究。E-mail:zhaowuliu@hotmail.com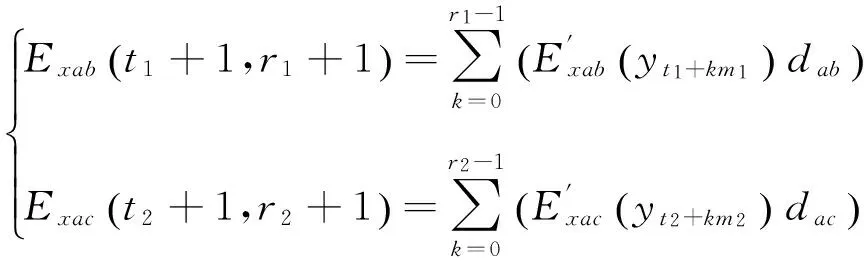
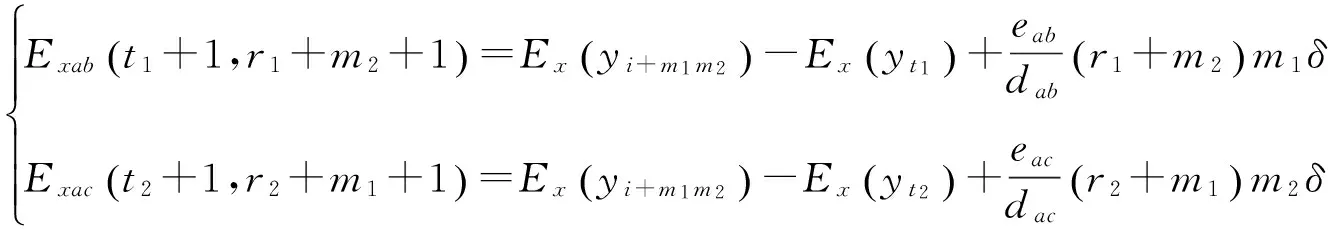
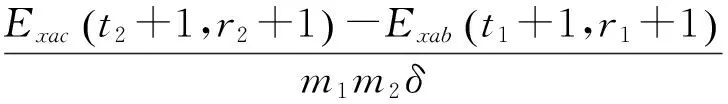
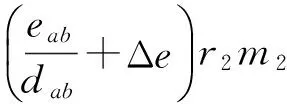
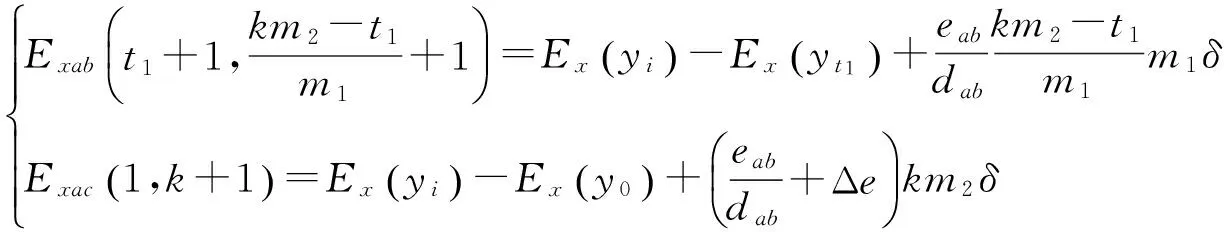
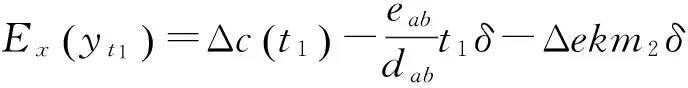
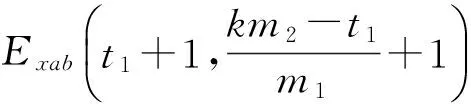

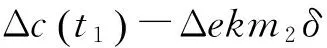
3 实验验证及结果讨论


4 结 论



