非均匀圆环形薄膜的径向格林函数计算

何　敏，王其申

(安庆师范大学 物理与电气工程学院，安徽 安庆 246133)



非均匀圆环形薄膜的径向格林函数计算

何敏，王其申

(安庆师范大学 物理与电气工程学院，安徽 安庆 246133)

格林函数在线性振动的定性研究中有重要应用，在质量轴对称分布的圆膜的格林函数基础上，计算了质量面密度是半径的单值函数时的圆环形薄膜的径向格林函数。

轴对称；圆环形薄膜；径向格林函数

1　膜的横振动方程和边界条件

对于一般的二维弹性薄膜，其质量面密度为ρ(x,y)，张力T视为常数，占有二维域Ω，并以∂Ω为边界，它作横向微振动时的模态方程为[3]T(uxx+uyy)+λρ(x,y)u(x,y)=0，(x,y)∈Ω

(1)式中u(x,y)是点(x,y)的位移振型函数，λ=ω2代表特征值，ω代表固有圆频率，ρ(x,y)是Ω上的正值性函数。一般的边界条件写为

(2)

式中n是区域外法向单位矢量，h代表边界处支承弹簧的刚度。若h→+∞，有u(x,y)=0，则膜的周边是固定的；而h=0对应膜的周边是自由的。

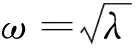
(3)

hu(a,θ)=0,0≤θ≤2π

(4)式中，k,h是位于圆环形薄膜内外边界弹簧的弹性系数，k,h≥0；当k(或h)为0时，圆环形薄膜的内(外)边界自由；当k(或h)→+∞时，圆环形薄膜的内(外)边界固定。采用分离变数法[3]，u(r,θ)=R(r)Φ(θ)，有

(5)

Φ″(θ)+m2Φ(θ)=0

(6)

(6)式与均匀圆膜的同一方程的解完全相同[4]。(5)式已不是一般意义上的贝塞尔方程，但仍属于斯图膜—刘维尔型方程，由(4)式经分离变量后的边界条件为

TR′(b)-kR(b)=0,TR′(a)+hR(a)=0

(7)

2　质量轴对称分布的圆环形薄膜格林函数的推导

经过简单的推导，圆环形薄膜的径向格林函数G(r,s)满足：

该公司是一家采用德国技术的外商独资企业，主要从事真空镀膜PVD设备和相关真空设备的制造和销售，同时提供应用于各种工业领域的硬质涂层服务。星弧涂层制造具有国际领先水平的Jupiter系列、Dimant系列和Seeyu系列PVD涂层设备，并提供完整成熟的镀膜工艺。此外，星弧涂层也可根据客户的具体要求设计制造高品质的真空镀膜设备。

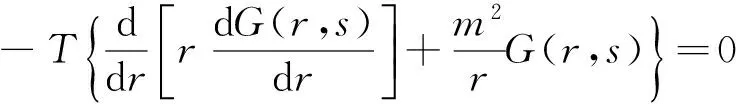
b≤r,s≤a

(8)

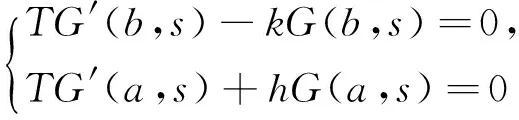
(10)(9)式为边界条件， (10)式为衔接条件，式中s代表位于区间(b,a)内的某个动点。(10)式中的第1式表示在s点作用一个单位集中力。

以下用构造法来得到同时满足(8)～(10)式的格林函数。令

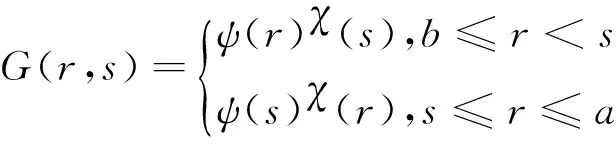
(11)

(10)式的第2个条件显然是满足的，而关于ψ(r), χ(r)的微分方程分别为

(12)

和

(13)

经过简单验证，函数ψ(r), χ(r)满足关系式：

.

显然有

(14)

和(10)式的第1式相比较，取C0=1/T。

说明方程求解需要的欧拉方程的求解结果[5]如下：

(12)、(13)两式中的方程属于欧拉型方程

x2y″+xy′-m2y=0。

令x=et,D=d/dt，将原方程改写为(D2-m2)y=0，它的特征方程为λ2-m2=0。

(1)当m=0时，特征方程有相等实根λ1=λ2=0，则欧拉型方程的根为

y=C1+C2lnx。

(2)当m≠0时，特征方程有相异实根λ1=m,λ2=-m，则欧拉型方程的根为

y=C3xm+C4x-m。

所以，当m=0时，由(12)～(14)式，解得

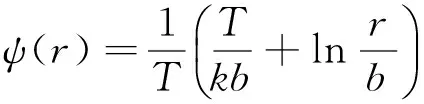
(15)

当m≠0时，由(12)～(14)式，解得

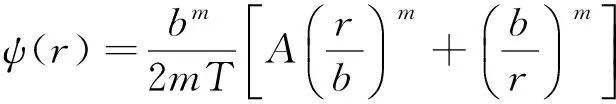
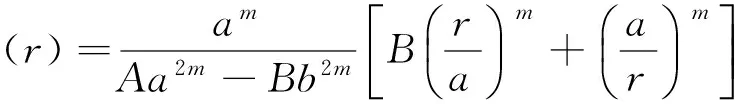
(16)

这里

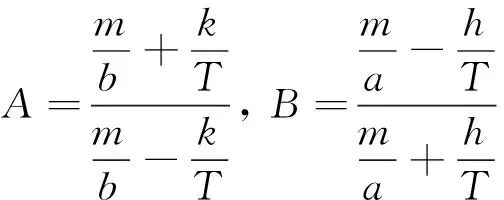
(17)

(18)

讨论若圆环形薄膜的边界固定，即k→+∞,h→+∞时，则将上述两式改写，

(20)

3　结束语

以上计算了m=0和m≠0两种情况下质量轴对称分布的圆环形薄膜的径向格林函数，由于内半径及圆环形薄膜内边界弹簧弹性系数k的引入，得到的圆环形薄膜的径向格林函数显然比圆膜的径向格林要复杂。这种质量轴对称分布的圆环形薄膜的径向格林函数具有一定的理论价值。对于质量任意分布的圆环形薄膜，即ρ=ρ(r,θ)，其格林函数的计算有相当难度，本文没有涉及，有待进一步研究。

[1] Gladwell G M L. Qualitative properties of vibrating systems[J]. Proc R Soc Lond A, 1985(401): 299-315.

[2] ГантмахерФ Р, КрейнМ Г. Осцилляцонные Матрицы и Ядра и Малые Колебания Механических Систем[M]. Москва: Государственное Издательство Технико-Теоретической Литературы, 1950: 82-288.

[3] 王大钧, 王其申, 何北昌. 结构力学中的定性理论[M]. 北京: 北京大学出版社, 2014: 235-237.

[4] Wu Lei, Wang Qishen, Wang Dajun, et al. Qualitative properties of vibration about non homogeneous circular membrane with axisymmetrical mass[J]. Advanced Materials Research, 2011, 216(3): 158-162.

[5] 四川大学数学系高等数学教研室. 高等数学(第三册)[M]. 北京: 高等教育出版社, 1990: 250-252.

Calculation of the Radial Green′s Functions of Inhomogeneous Annular Membrane

HE Min, WANG Qi-shen

(School of Physical & Electrical Engineering, Anqing Normal University, Anqing, Anhui 246133, China)

The Green′s function in the qualitative research of linear vibration has important applications. Based on the radial Green′s function of circular membrane with axial symmetry mass distribution, the radial Green's function of annular membrane is calculated when the mass surface density is the single valued function of radius.

axial symmetry; circular membrane; the radial Green′s function

2015-08-01

国家自然科学基金(10772001)和安徽高校省级自然科学研究重点项目(KJ2016A429)。

何敏，男，安徽巢湖人，硕士，安庆师范大学物理与电气工程学院副教授，研究方向为振动的定性性质和反问题。E-mail: hemm@aqnu.edu.cn

时间：2016-8-17 11:31

http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.016.html

O32

A

1007-4260(2016)03-0055-02

10.13757/j.cnki.cn34-1150/n.2016.03.016