Hilbert空间中一类上下界均衡问题解的存在性

赵 方 浩

(南京财经大学 应用数学学院，江苏 南京 210003)



Hilbert空间中一类上下界均衡问题解的存在性

赵 方 浩

(南京财经大学 应用数学学院，江苏 南京 210003)

在Hilbert空间中讨论了一类上下界均衡问题解的存在性，在研究过程中，把上下界均衡问题转化为带对称界均衡问题，在定义域为紧集和非紧集两种情况下，分别给出了相关存在性定理，推广了文献[1，6]中的相应结果。

上下界；均衡问题；紧性；非紧性

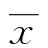
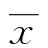
1　预备知识

总假设X为Hilbert空间，X上的内积记为〈·,·〉，由该内积诱导的范数记为‖·‖，由该范数诱导的度量记为d。 X中非空子集构成的集族记为2X，D为X的子集，0为X中的零元，R为实数集。

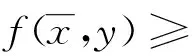
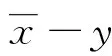
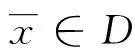
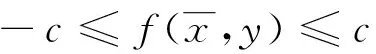
注1带上下界均衡问题总可以通平移变换转化成带对称界均衡问题，因为

c1≤f(x,y)≤c2⟺

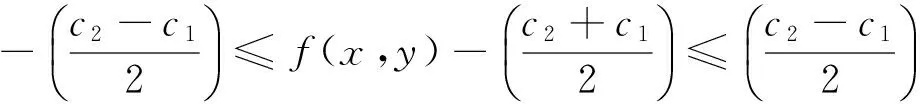
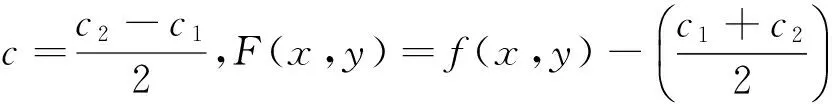
由注1可知带上下界均衡问题总可以通过平移变换转化成带对称界均衡问题，故下面只需研究带对称界均衡问题(SBEP)。

下面给出了Hilbert空间中均衡问题解的存在性，即引理1。

引理1设D为X的闭子集，如果映射f∶D×D→R满足下列条件：

(1)对∀x∈D，f(x,·)下半连续且下有界，

(2)对∀x∈D，f(x,x)=0，

(3)对∀x,y,z∈D，都有f(z,x)≤f(z,y)+f(y,x)，

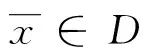
证明不失一般性，只证明ε=1的情况。记

F(x)={y∈D∶f(x,y)+‖y-x‖≤0}

由(1)知，对∀x∈D，F(x)是闭集；由(2)知，

x∈F(x)，故F(x)是非空集合。设y∈F(x)，即f(x,y)+‖y-x‖≤0，令z∈F(x)[即f(y,z)+‖y-z‖≤0]不等式两边相加，由(3)可得，

0≥f(x,y)+‖y-x‖+f(y,z)+‖y-z‖≥

f(x，z)+‖z-x‖，即z∈F(x)，因此y∈F(x)意味着F(y)⊆F(x)。

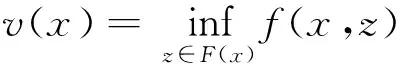
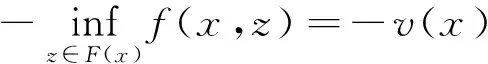
即

‖x-z‖≤-v(x)，∀z∈F(x)。

特别地，如果x1,x2∈F(x)，‖x1-x2‖≤‖x-x1‖+‖x-x2‖≤-v(x)-v(x)=

-2v(x)，则diam[F(x)]≤-2v(x)，∀x∈D。

固定x0∈D，存在x1∈F(x0)使得f(x0,x1)≤v(x0)+2-1。记x2为F(x1)的任意一点有

f(x1,x2)≤v(x1)+2-2。重复上述步骤，可以定义一个序列{xn}∈D，且xn+1∈F(xn)使得

f(xn,xn+1)≤v(xn)+2-(n+1)。

注意到

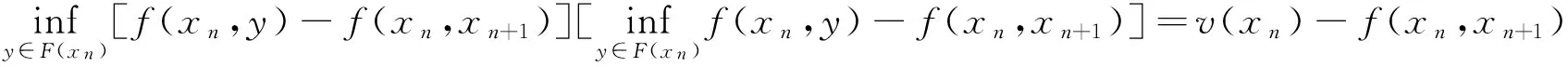
因此v(xn+1)≥v(xn)-f(xn,xn+1)，

且-v(xn)≤-f(xn,xn+1)+2-(n+1)≤

[v(xn+1)-v(xn)]+2-(n+1)，

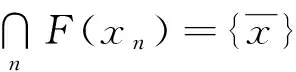
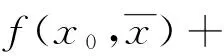
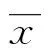
2　紧集上SBEP解的存在性

定理1设D为X的紧子集，如果映射f∶D×D→R满足下列条件：

(1) 对∀x∈D，f(x,·)下半连续，

(2) 对∀x∈D，f(x,x)=0，

(3) 对∀x,y,z∈D，都有f(z,x)≤f(z,y)+f(y,x)，

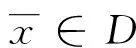
证明对∀n∈N+，令xn∈D是一个ε均衡点 (由引理1可知该点存在)，即

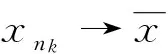
注2定理1推广了文献[1]中推论3.2。

推论1设D为X的紧子集，如果映射f∶

D×D→R满足下列条件：

(1)对∀x∈D，f(x,·)下半连续，

(2)对∀y∈D，f(·,y)上半连续，

(3)对∀x∈D，f(x,x)=c，

(4)对∀x,y,z∈D,都有|f(z,x)|+c≥

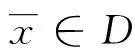
证明令F(x,y)=c-|f(x,y)|，由(1)可得对∀x∈D，F(x,·)下半连续。由(2)得，对∀y∈D，F(·,y)上半连续，由(3)可得，对∀x∈D，F(x,x)=c-c=0；下证对∀x,y,z∈D,都有F(z,x)≤F(z,y)+F(y,x)，由(4)可知

|f(z,x)|+c≥|f(z,y)|+|f(y,x)| ，

-|f(z,x)|-c≤-|f(z,y)|-|f(y,x)| ，

所以

c-|f(z,x)|≤c-|f(z,y)|+c-|f(y,x)| ，

F(z,x)≤F(z,y)+F(y,x)。

注3推论1同时是对文献[6]中定理5.1的改进和推广 。

3　非紧集上SBEP解的存在性

定理2设D为X的子集，‖·‖为X上的内积诱导的范数，若映射f∶D×D→R满足：

(1)对∀x∈D，f(x,·)下半连续且下有界，

(2)对∀x∈D，f(x,x)=0，

(3)对∀x,y,z∈D，都有f(z,x)≤f(z,y)+f(y,x)，

(4)对∀y∈D，f(·,y)上半连续，

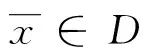
证明不失一般性，不妨设Kr非空，对∀x∈D，考虑下面的非空集合

S(x)={y∈D∶‖y‖≤‖x‖∶f(x,y)≤0}，

对∀x,y∈D，y∈S(x)，有S(y)⊆S(x)。事实上，对z∈S(y)，有‖z‖≤‖y‖≤‖x‖，由(3)得f(x,z)≤f(x,y)+f(y,z)≤0；另一方面，由于Kr是紧的，由(1)可得，对∀x∈D，S(x)⊆Kr是紧集，进一步，由定理1，∃xr∈Kr使得

f(xr,y)≥0,∀y∈Kr，

(1)

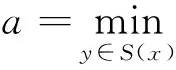
下面分两种情况讨论。

情况1a≤r，令y0∈S(x)，使得‖y0‖=a≤r，则有f(x,y0)≤0。由于f(xr,x)≤0且由条件(3)可得f(xr,y0)≤f(xr,x)+f(x,y0)≤0,此不等式与(1)式矛盾。

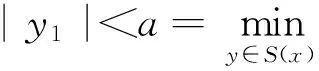
注4定理2是对文献[1]中定理4.1的推广。

推论2设D为X的紧子集，‖·‖为X上的内积诱导的范数，若映射f∶D×D→R满足：

(1) 对∀x∈D，f(x,·)下半连续且下有界，

(2) 对∀x∈D，f(x,x)=c，

(3) 对∀x,y,z∈D，都有|f(z,x)|+c≥

|f(z,y)|+|f(y,x)| ，

(4) 对∀y∈D，f(·,y)上半连续，

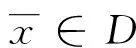
证明令F(x,y)=c-|f(x,y)|，易证F(x,y)满足定理2中的条件(1)～(4)其证法与推论1的相同，此处省略。下面证明F(x,y)满足定理2的条件(5)，因为∃r>0，对∀x∈DKr都∃y∈D，‖y‖≤‖x‖，使得

f(x,y)≥c，f(x,y)≥c，可知|f(x,y)|≥c，所以

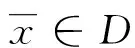
注5定理2是对文献[6]中定理5.2的改进和推广。

[1]BianchiM,KassayG,PiniR.ExistenceofequilibriaviaEkeland’sprinciple[J].MathematicalAnalysisandApplications, 2005, 305: 502-512.

[2]AllecheB,RădulescuVD.TheEkelandvariationalprincipleforequilibriumproblemsrevisitedandapplications[J].NonlinearAnalysis, 2015, 23: 17-25.

[3]CohenG.Auxiliaryproblemprincipleextendedtovariationalinequalities[J].OptimTheoryAppl, 1988, 59:325-333.

[4]FanK.AgeneralizationofTychonoff’sfixedpointtheorem[J].MathAnnalen, 1961, 142: 305-310.

[5]张从军. 一类具有上下界均衡问题[J]. 数学学报, 2005, 48(2): 293-298.

[6]王月虎. 均衡问题及其经济应用[D]. 安徽: 安徽大学, 2015.

[7]YuanGXZ.TheStudyofMinimaxInequalitiesandApplicationtoEconomicsandVariationalInequalities[M].NewYork:AmericanMathematicalSociety, 1998: 1-140.

[8]YuanGXZ.KKMTheoryandApplicationsinNonlinearAnalysis[M].Florida:CRCPress, 1999:1-648.

[9]DingXP.Constrainedmulti-objectivegamesinlocallyconvexH-spaces[J].AppliedMathematicsandMechanics, 2003, 24(5): 441-449.

[10]ChadliO,ChbaniZ,RiahiH.RecessionmethodsforequlilbriumproblemsandapplicationstoVariationalandhemivariationalinequalities[J].DiscreteandContinuallyDynamicalSystems,1999, 5: 185-195.

[11]ChadliO,ChbaniX,RIahiH.Equilibriumproblemsandnoncoercivevariationalinequalities[J].Optimization, 2001, 50(1): 17-27.

[12]IsacG,SehgalVM,SinghSP.AnalternateversionofaVariationalinequality[J].IndianJofMath, 1999, 41(1): 25-31.

Existence of Equilibrium Problems with Lower and Upper Bounds in Hilbert Space

ZHAO Fang-hao

(Department of Applied Mathematics, Nanjing University of Finance and Economics,Nanjing, Jiangsu 210003, China)

In this paper, we discuss the existence of equilibrium problems with the upper and lower bounds. In the process of study, the equilibrium problem of the upper and lower bounds is transformed into symmetric bounded equilibrium one. In both cases of the domain of compact set and non-compact set, some related theorems are given respectively. In addition, the corresponding results in literature [1,6] are generalized.

upper and lower bounds; equilibrium problems; compact; non-compact

2015-12-29

赵方浩，男，河南开封人，南京财经大学应用数学学院硕士研究生，研究方向为非线性分析与经济应用。E-mail: zfhzs2015@163.com

时间：2016-8-17 11:31

http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.002.html

O29

A

1007-4260(2016)03-0005-03

10.13757/j.cnki.cn34-1150/n.2016.03.002