矩阵迹的Young不等式和反向Young不等式的应用

周 其 生

(安庆师范大学 数学与计算科学学院，安徽 安庆 246133)



矩阵迹的Young不等式和反向Young不等式的应用

周 其 生

(安庆师范大学 数学与计算科学学院，安徽 安庆 246133)

运用矩阵迹的Young不等式和Lieb-Thirring不等式给出一个矩阵迹的反向Young不等式，然后利用矩阵迹的Young不等式和反向Young不等式得到若干矩阵迹的不等式，所得结果推广了文献[7]的结果。

矩阵；迹；不等式

通常的Young不等式：

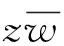
(1)

(2)Ando[1]将(1)式推广为n阶复矩阵对A,B特征值的不等式：

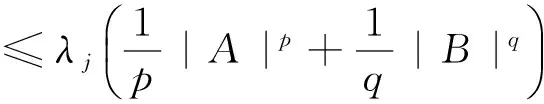
j=1,2,…,n

特别地，有矩阵迹的Young不等式

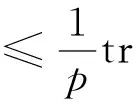
(4)

等号当且仅当|A|p=|B|q时成立，记号trA表示矩阵A的迹。

当A,B为n阶半正定Hermite矩阵时，有

(5)

等号成立当且仅当Ap=Bq。

(5)式可等价地写成

tr(AvB1-v)≤vtr(A)+(1-v)tr(B),v∈(0,1)

(6)

最近，Manjegani和Norouzi[2]给出矩阵形式的反向Young不等式：设A,B为n阶非奇异复矩阵，v∈(1,∞)，则存在酉矩阵U使得

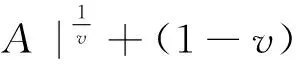
(7)

(7)式中的酉矩阵U一般是必要的，文[2]中为说明当AB≠BA时(7)式无酉矩阵U不成立，举例如下：

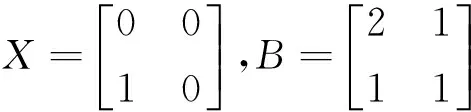
tr(|AvB1-v|)≥tr[vA+(1-v)B]

(8)

本文先证明一个优于(8)式的矩阵迹的反向Young不等式，然后利用此式得到一类矩阵迹的不等式，最后基于同样的方法和Young不等式得到另一类不等式。

对于两个半正定Hermite矩阵A,B，一个重要事实是A,B的乘积AB可对角化[3-4]，从而对任何正数α,利用AB的谱分解知(AB)α有明确意义。Lieb和Thirring[5]给出如下不等式(Lieb-Thirring不等式)：

tr(AB)α≤tr(AαBα),α≥1

(9)

Wang等[6]推广了(9) 式对满足|α|≥1的实数成立，|α|≤1时成立反向不等式，并且给出等号成立的充要条件为α=-1,0,2或AB=BA。利用(5)式和(9)式，可得如下定理。

定理1设A为半正定Hermite矩阵，B为与A同阶的正定Hermite矩阵，对任何实数v≥1，有

tr(AvB1-v)≥vtrA+(1-v)trB

(10)

等号成立当且仅当v=1或A=B。

证明v=1时不等式等号显然成立。下面仅需考察v>1时的情形：由矩阵迹的性质tr(AB)=tr(BA)及Young不等式(5)得

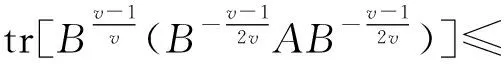
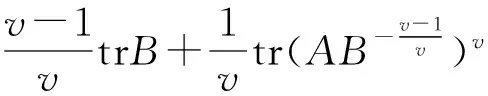
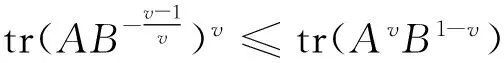
注意到tr(|AvB1-v|)≥tr(AvB1-v)，并且严格不等式是可能实现的，例如：

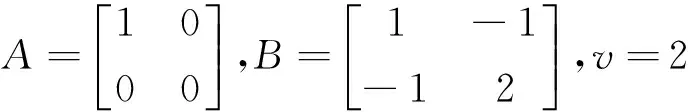
故定理1的结果优于(8)式，相对于(6)式，称(10)式为矩阵迹的反向Young不等式。

下面利用矩阵迹的反向Young不等式(10)证明一些矩阵迹的不等式，并推广了文献[7]的若干结果。

定理2设A1,A2,…,An(n>1)为同阶半正定Hermite矩阵，且任意n-1个之和可逆，v≥1，则

(12)

等号成立当且仅当v=1或A1=A2=…=An。

证明对任意实数α>0，在定理1中以αA1代替A，A2+…+An代替B，得

vαtrA1+(1-v)tr(A2+…+An)，

同理可得其余各式：

vαtrA2+(1-v)tr(A3+…+An+A1)，

…，

vαtrAn+(1-v)tr(A1+…+An-1)。

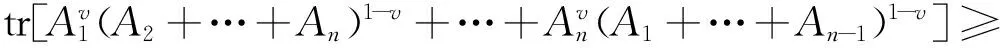
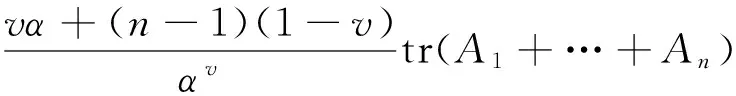
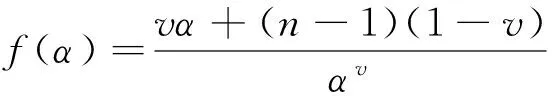
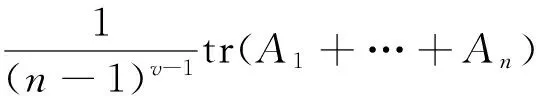
同理可证(12)式及等号成立的条件。

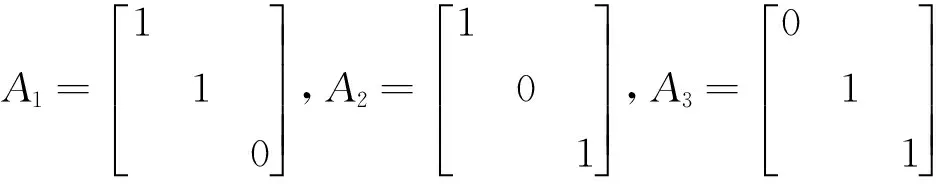
注2当v=2和v=n时，定理2分别是文[7]中定理3和定理4。

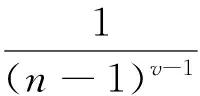
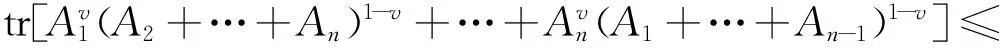
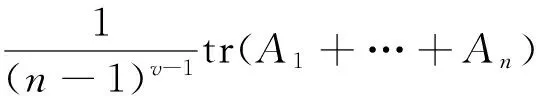
等号成立当且仅当A1=A2=…=An。

下面定理与定理1类似，利用Young不等式得到：

定理4设A为半正定Hermite矩阵，B为与A同阶的正定Hermite矩阵，则对任何实数v≥2和实数μ，有

tr(AvB-μ)≥2tr(Av-1B1-μ)-tr(Av-2B2-μ)

(13)

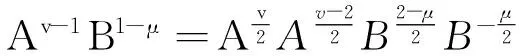
tr(Av-1B1-μ)=

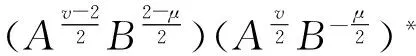
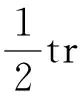
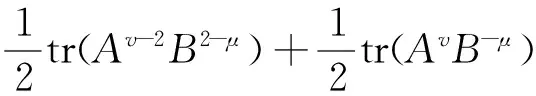
如果定理4中的A也为正定的，则有

定理5设A,B为同阶正定Hermite矩阵，则任何实数v,μ有

tr(AvB-μ)≥2tr(Av-1B1-μ)-tr(Av-2B2-μ)

(14)

利用这两个定理，可以得到以下一些不等式。

(16)

证明在(14)式中以αA代替A，以A2+…+An代替B，并令μ=1得

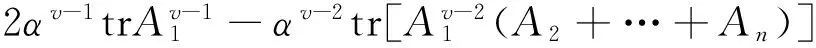
(17)

由Young不等式(5)可得

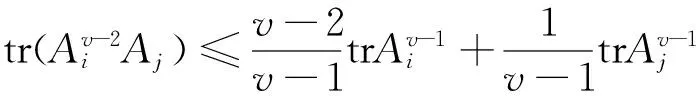
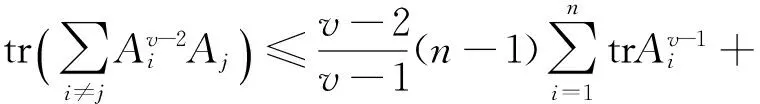
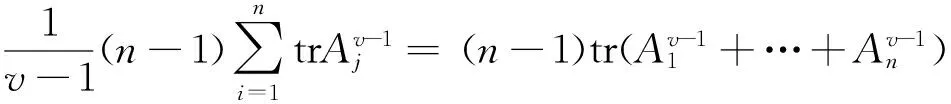
同理可证(16)式。

注3定理6的条件若改为“A1,A2,…,An(n>1)为同阶半正定Hermite矩阵，且任意n-1个之和可逆”，则当v≥2时，利用定理4的(13)式，便知不等式(15)和(16)仍成立。此时v=2,3,k分别为文[7]中定理3,6,7的推广。

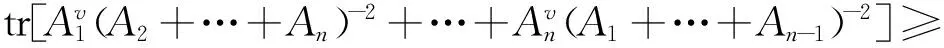
(19)

证明记S=A1+A2+…+An，在定理4中依次以αAi代替A，以S-Ai代替B，并令μ=2，得

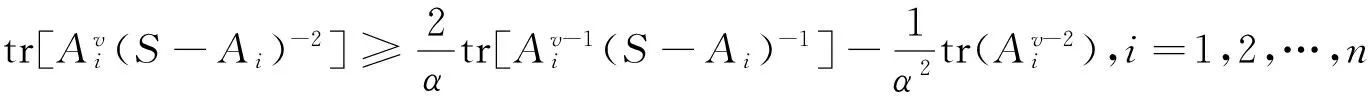
将各式两边分别相加得

由定理6知，

代入前一式得

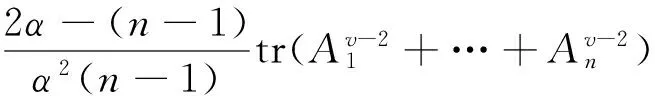
取最佳常数α=n-1，得(18)式。同理可证(19)式成立。

同样，利用定理5可得

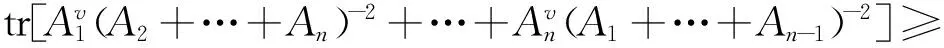
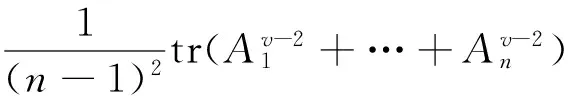
定理7和定理8是文[7]中定理8的一般化。

[1]AndoT.MatrixYounginequlities[J].OperTheoryAdvAppl,1995, 75: 33-38.

[2]ManjeganiSM,NorouziA.MatrixformoftheinverseYounginequalities[J].LinearAlgebraAppl,2015, 486: 484-493.

[3]HongY,HornRA.TheJordancanonicalformofaproductofaHermitianandapositivesemidefinitematrix[J].LinearAlgebraAppl, 1991,147: 373-386.

[4]WuPW.Productsofpositivesemidefinitematrices[J].LinearAlgebraAppl, 1988,111: 53-61.

[5]LiebEH,ThirringW.StudiesinMathematicalPhysics[M].Princeton:PrincetonUniversityPress, 1976.

[6]WangBY,ZhangFZ.TraceandeigenvalueinequalitiesforordinaryandHadamardproductsofpositivesemidefiniteHermitianmatrices[J].SIAMJournalonMatrixTheoryandApplications, 1995, 16: 1173-1183.

[7]周其生，金乐乐. 一类矩阵迹的不等式[J].安庆师范学院学报(自然科学版)，2015, 21(3)：1-4.

Applications of Young Inequality and Inverse Young Inequality for Matrix Trace

ZHOU Qi-sheng

(School of Mathematics and Computation Science, Anqing Normal University, Anqing, Anhui 246133, China)

We provide an inverse Young inequality for Matrix Trace by using Young inequality and Lieb-Thirring inequality in matrix trace, and then use a matrix trace inequality Young and reverse Young to get a number of a matrix trace inequality. The obtained results generalize the results of [7].

matrix; trace; inequality

2016-02-25

周其生，男，安徽金寨人，安庆师范大学数学与计算科学学院教授，主要研究方向为算子理论。E-mail: zhouqish@aqnu.edu.cn

时间：2016-8-17 11:31

http://www.cnki.net/kcms/detail/34.1150.N.20160817.1131.001.html

O178；O151.21

A

1007-4260(2016)03-0001-04

10.13757/j.cnki.cn34-1150/n.2016.03.001