基于小尺度数值模型的海底滑坡运动敏感性分析

修宗祥，刘乐军，解秋红，李西双，胡光海，李家钢，赵强

（1.国家海洋局第一海洋研究所，山东　青岛　266061；2.海岸和近海工程国家重点实验室，辽宁　大连　116024；3.中海油研究总院，北京　100027）

基于小尺度数值模型的海底滑坡运动敏感性分析

修宗祥1，2，刘乐军1，解秋红1，李西双1，胡光海1，李家钢3，赵强1

（1.国家海洋局第一海洋研究所，山东青岛266061；2.海岸和近海工程国家重点实验室，辽宁大连116024；3.中海油研究总院，北京100027）

开展海底滑坡运动特性研究是深水陆坡区滑坡地质灾害认识与防治的基础，建立了基于非牛顿流体欧拉-欧拉两相流理论的小尺度海底滑坡数值模型。在与实验数据和BING程序结果对比验证的基础上，模拟分析海底滑坡的一般运动规律及特性，并同无水条件下的滑坡模拟结果进行了对比。结果表明：环境水的存在可引发“滑水”现象，延长滑坡运动时间，增加运动距离，但端部最大峰值速度相对无水条件时较小；滑坡体物质组成、地形坡度、初始速度、初始厚度等因素，对最终的运动距离有较大的影响；滑坡体在运动过程中因扰动、混水而导致的屈服强度和粘滞系数的不断降低是海底滑坡长距离运动的主要原因。

海底滑坡；欧拉-欧拉两相流模型；Herschel-Bulkley模型；滑水；软化

深水陆坡区海底滑坡产生的高速滑动，可能给海底管道等设施造成破坏性影响 （Locat et al，2002；Nadim et al，2005；Mosher et al，2010）。由于陆坡区水深较大，海底地貌崎岖复杂，海底管道一旦破坏，不但维修难度和费用较大，还会带来严重的环境问题。因此，海底管道设计与路由选择必须考虑海底滑坡地质灾害的影响（Parker et al，2008；Randolph et al，2010；Yuan et al，2015）。而开展海底滑坡运动规律特性研究，分析土的组成、地形坡度、初始速度、初始厚度等因素与运动速度、距离的关系，有利于提高对陆坡区海底滑坡地质灾害认识。

限于观测条件限制，室内物理实验与数值模拟成为研究海底滑坡运动特性的主要手段（Locat et al，2002；Wright et al，2007）。而数值模拟技术作为一种快速有效的方法，近年来已被广泛采用。Imran等（2001a）采用Herschel-Bulkley和双线性流变模型模拟海底滑坡运动，该模型未能考虑“滑水”现象与Mohrig等（1998）的部分实验结果不符。Harbitz等（2003）基于润滑理论提出了稳定“滑水”状态下的一维模型，模型忽略了前部、尾部及顶部的动水压作用，但研究表明动水压作用是十分重要的 （Wright et al，2007；Ilstad et al，2004a）。De Blasio等（2005）在Imran等人的基础上将滑坡滑动过程分为初始流动、产生水楔、“滑水”、“滑水”停止的四阶段模型，该模型与实验符合较好，但临界Froude数、初始水楔形状、滑坡土体与海床间的粗糙度高度参数等均为人为假定。多相流理论近年来被引入到海底滑坡模拟中（Gauer et al，2006；Xiu et al，2015），室内实验对比证明该方法可以有效模拟“滑水”现象，为海底滑坡机理研究提供了新的途径。

目前国内海底滑坡相关研究主要集中在前期的参数识别、触发机制与稳定性研究方面（刘保华等，2005；吴时国等，2008；刘杜娟等，2010；胡光海，2011；彭俊等，2014；刘乐军等，2014），针对滑后的运动特性研究相对较少。考虑实际海底滑坡的复杂性和多样性，本文通过小尺度欧拉-欧拉两相流数值模型探讨海底滑坡运动的一般特性，并分析了多种工况参数对滑坡滑动影响的敏感性。研究结果可为我国深水陆坡海底滑坡地质灾害认识与防治提供参考。

1　欧拉-欧拉两相流模型

两相流模型中环境水采用牛顿流体模拟，滑坡体可以看作粘塑性流体（Imran et al.，2001a），其流变特性可以由Herschel-Bulkley模型表达

其中，τC为屈服应力，γ˙为剪切速率，K为粘度系数，n为流动指数。滑坡体与水的相互作用可采用欧拉-欧拉两相流模型模拟。忽略滑坡运动运动过程中的热传导作用，流体基本控制方程如下

质量守恒方程：

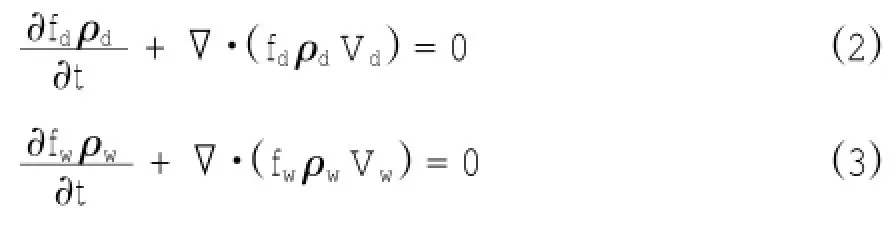
式中，▽为梯度算子，ρd，ρw，fd，fw，Vd，Vw分别为滑坡体与水的密度、体积分数以及速度向量，其中fw=1-fd。滑坡体与水的动量平衡方程如下：

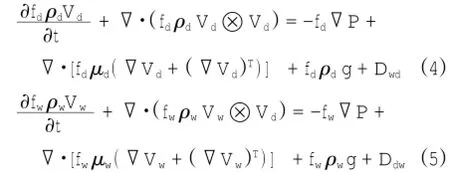
其中，P为压力，g为重力加速度，μd、μw分别为滑坡体和水的有效粘度，Dwd与Ddw为滑坡体与水在交界面处的相互作用力。滑坡体采用层流模型，环境水采用k-ε湍流模型模拟。

2　两相流模型验证

为了验证两相流模型的有效性，分别与文献（Imran et al，2001 b）中的实验数据及BING程序结果（其中笔者对BING模型进行简单修改，以模拟初始形状为矩形的情况）进行了对比。实验中将膨润土合成泥浆从容器倒入3.44°倾角的矩形槽中。泥浆初始长度L=1.8 m，初始厚度为H=0.3 m，泥浆密度ρd=1 073 kg/m3，屈服强度τy=42.5 Pa，参考应变速率γr=193.2 s-1。限于尺寸，仅给出两相流模型局部示意图，见图1。其中，泥浆采用Bingham流体，环境空气采用牛顿流体，流体单元总数164 360个，计算步长0.002 s。模型顶部为压力开放边界，前后两侧采用对称边界，左右两侧采用自由滑动边界。BING程序单元数取21，时间步长取1×10-6。计算结果可以看出（图2），两相流模型模拟结果，与BING模型结果接近，与实验值误差约为6%。考虑到数值模型因在左侧设置墙边界以阻止泥浆向后流动，可能会导致计算结果稍大。认为两相流模型的结果是可靠的。

由于目前公开文献中尚未有提供水环境下数值模拟所需的全部实验初始参数。这里仅对两相流模型与BING模型结果进行比较。BING忽略了环境水的动力作用，仅考虑静水压的影响。通过对比可体现出两相流模型的优越性。根据文献（Ilstad et al，2004 b）数据，设泥浆为Bingham流体，环境水采用牛顿流体，泥浆密度ρd=1 600 kg/m3，屈服强度τy=60 Pa，粘度系数K=0.035 Pas。斜坡角度6°，泥浆初始形状采用矩形条带，长度L=2 m，初始厚度分别为0.3 m和0.5 m两种情况。

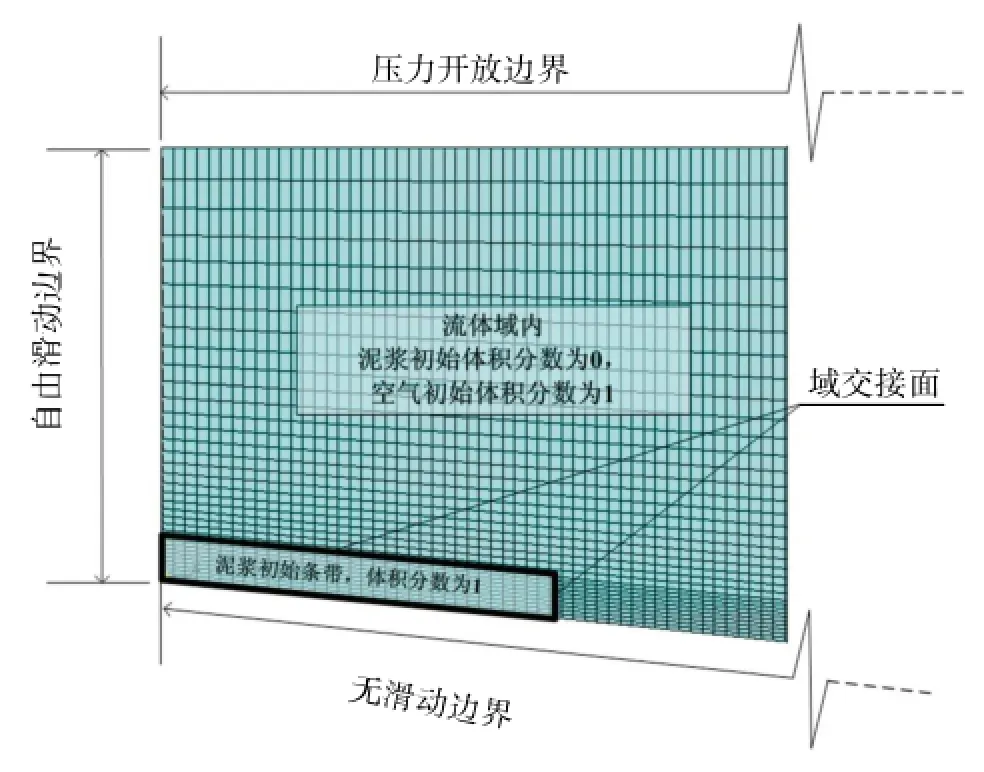
图1　局部两相流模型

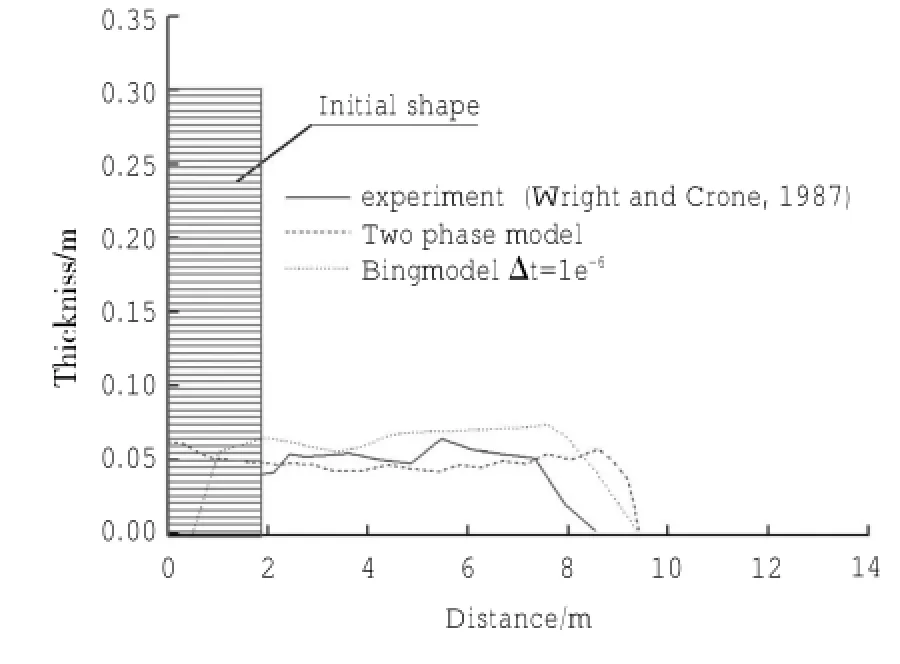
图2　最终形态对比

图3为两种方式下泥浆端部到达不同位置时对应的速度值。可以看出，两相流模型所得到的峰值速度小于BING模型模拟值，这主要是由于BING模型没有考虑水的阻力，而两相流模型考虑了泥浆与水的动态相互作用。同时由图4和图5可以看出，虽然存在水的阻力作用，但两相流模型的最终滑动距离却并未减小，这主要是由于泥浆滑动过程中发生“滑水”效应所致。图3中两相流模型的泥浆端部速度变化趋势也与之相符，即在前半部分保持在一定的速度，之后慢慢衰减。图4中红圈位置拉伸作用明显，也主要是由于泥浆端部因滑水导致其速度相对后部较快产生的。Morrig等根据实验曾给出的滑水启动的临界速度条件

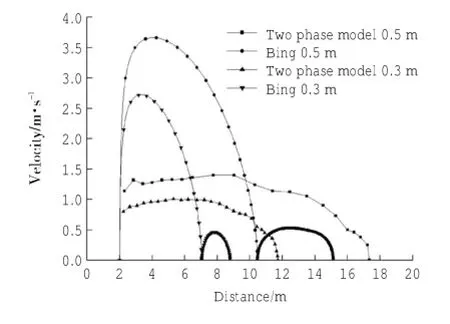
图3　端部速度变化对比

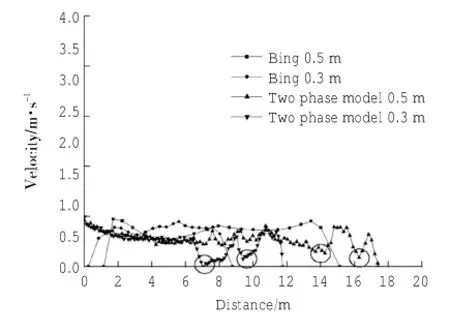
图4　两相流模型与BING最终形态对比

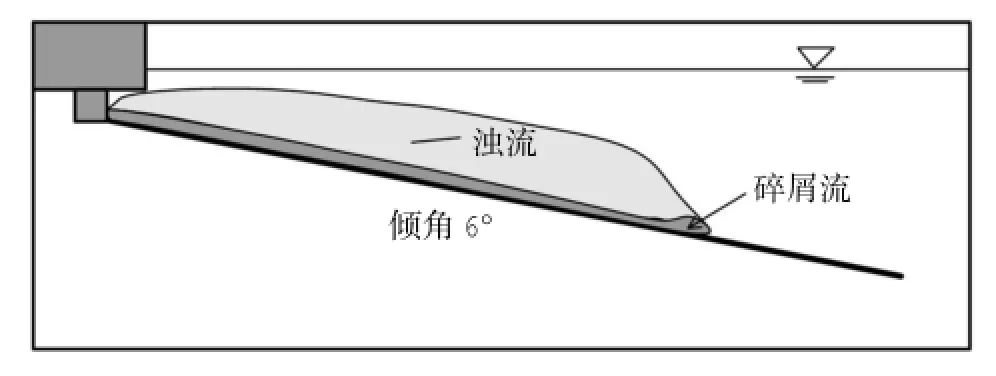
图5　水槽实验设计图

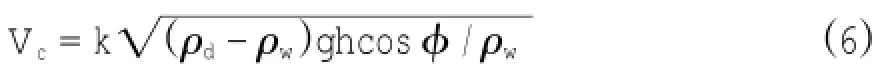
其中，Vc为滑水启动时泥浆前端的临界速度；h为端部的厚度；φ为斜坡角度；k为密度傅汝德数，约为0.3～0.4。若取保守值k=1，则根据公式（6），泥浆端部厚度范围0.15～0.3之间的滑水临界速度区间为0.94～1.32，这也与两相流模型的速度曲线相符合。由上述对比可以看出两相流模型适合计算水与土体的相互作用。

3　滑坡运动特性及参数敏感性分析

3.1模型设计

参考Ilstad等（2004b）实验（图5），设计数值模型如图6。假定初始滑坡体为矩形并具有一定初始速度。由于实际海底滑坡初始形状接近矩形（L'Heureux et al，2013），且地震等因素触发的滑坡会具有一定的初始动能，所以这种假设具有一定的实际意义。两相流数值模型长为16 m，同时设计了1°、3°和6°3种坡度以考虑地形坡度的影响。为了对比水下滑坡与陆地滑坡的不同，同时对无水条件下的运动进行了模拟。为估算网格数量对模拟结果的影响，计算了85 000和170 000两种单元数目下的最终运动距离，两者基本相同，因此本文计算均选择85 000网格数进行计算。

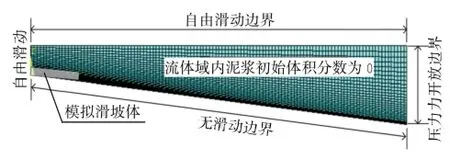
图6　模型图

数值模型中模拟滑坡体的力学参数，根据实验中的4种工况选取。不同粘土含量下的工况定性代表了不同物质组成的滑坡体。其中，模拟滑坡的泥浆由高岭土（ρ=2 650 kg/m3）、石英砂（ρ=2 750 kg/m3）以及水按质量分数比例混合而成，混合后密度ρ= 1 690 kg/m3。其流变特性由流变仪测出，表1为4种不同粘土含量下泥浆的Herschel-Bulkley模型拟和参数，计算过程中将公式（1）转化为表观粘度表达式，即μ=τC/Kγ˙+Kγ˙n-1。同时，针对每种材料工况分别进行了不同初始厚度与初始速度下的模拟对比，以讨论不同因素对海底滑坡滑动过程的影响。初始厚度根据实验观测值分别选取0.1 m、0.2 m、0.3 m、0.4 m、0.5 m。初始速度分别选取了0.5 m/s、1.0 m/s、1.38 m/s、1.5 m/s、2 m/s，中间工况1.38 m/s为根据实验浆体总体积、出口面积以及灌入时间求出的平均值。

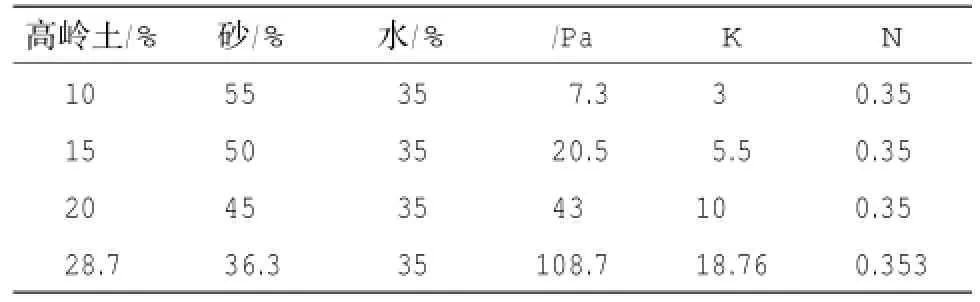
表1　不同粘土含量泥浆参数

3.2参数变化的影响

图7为初始模型高为0.5m，初始速度为1.0 m/s时，针对4种不同粘土含量浆体最大滑动距离。可以看出，粘土含量对滑动距离影响明显，随着粘土含量的增加，最大运移距离显著降低，且接近指数衰减。说明不稳定海床的物质成分组成，决定着海床土的力学性质，是影响海底滑坡滑动距离的关键因素。不考虑水动力条件下的模拟值，明显小于考虑水动力时的模拟值，粘度含量越低、地形坡度越大，两者差异越明显。

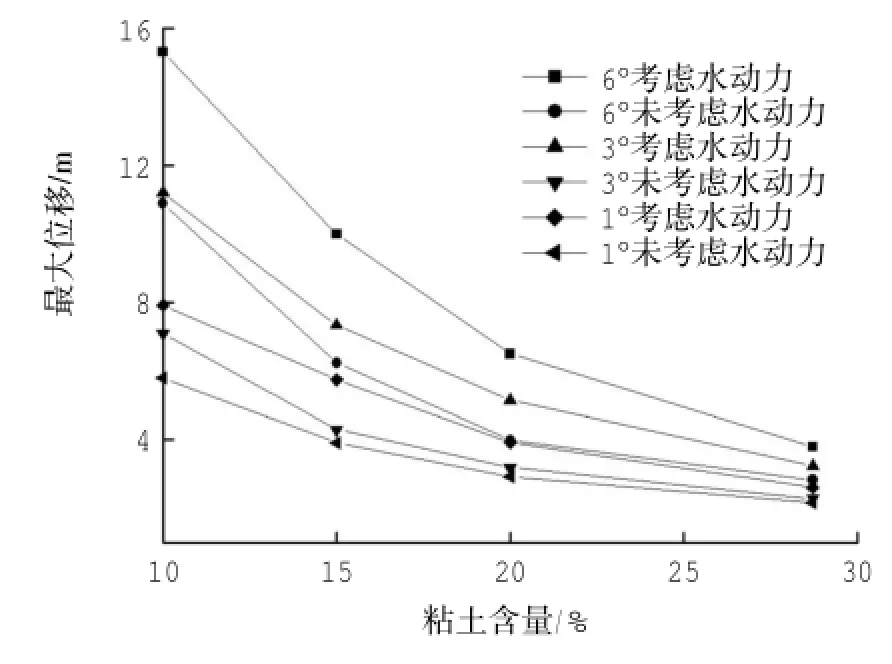
图7　最大运移距离随粘土含量变化曲线

图8为粘土含量为28.7%、初始高度为0.5 m时，不同初始速度下滑坡的最大运移距离。可以看出考虑水动力影响的最大运移距离仍然明显高于不考虑水动力时的运移距离。随着初始速度的增大，最大运移距离也相应较大。表明能够给滑坡体带来一定初始动能的触发机制（如地震等）可能会造成较大的滑动距离。

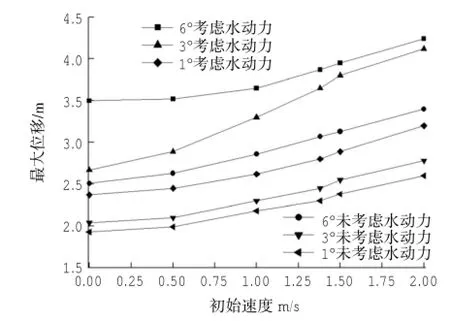
图8　最大距离随初始速度变化曲线（粘土含量28.7%）

图9为初始速度为1.38 m/s时，不同初始厚度下对应的最大运动距离。可以看出，不管是有水还是无水工况下，最大滑动距离都随着初始厚度的增加而增大，接近于幂增长函数。说明相同条件下，滑坡厚度越大，滑动距离往往越大。相比之下，考虑水动力作用时，厚度变化对最大运移距离影响较不考虑水动力作用时更敏感。

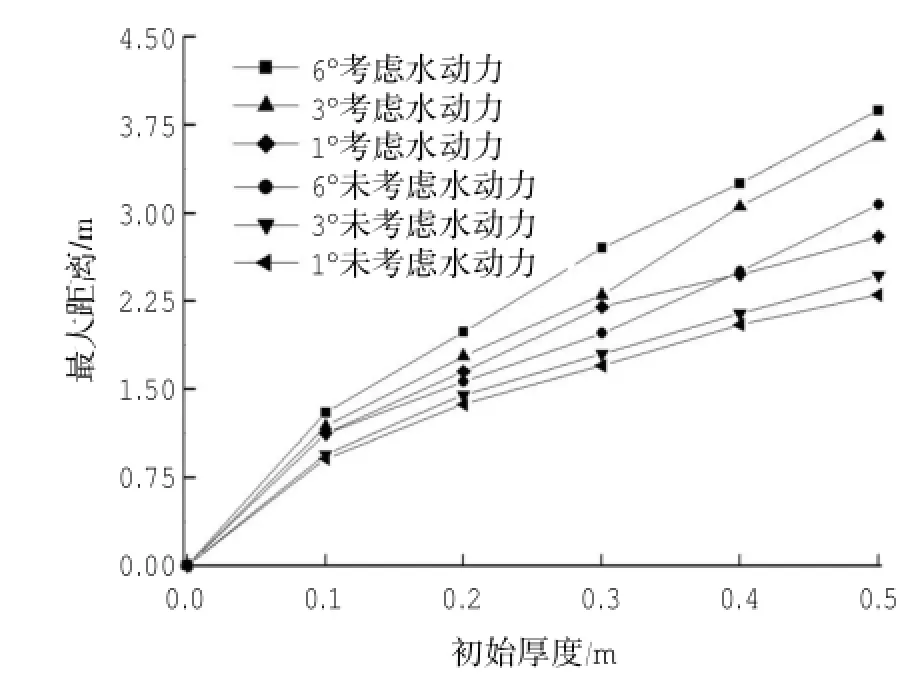
图9　最大距离随初始厚度变化曲线（粘土含量28.7%，初始速度1.38 m/s）

3.3水动力作用

3.3.1水动力作用

由前文计算结果可以看出，水动力作用能对滑坡运动距离产生较大的影响。水对滑坡体主要影响方式有两种：形成水楔而启动“滑水”现象与混入降低强度。“滑水现象”主要是由于滑坡土体快速运动时，在其底部形成类似水楔的水层。图10为28.7%粘土含量，在6°斜坡、初始速度1 m/s工况下，1.5 s时的体积分数云图，此时最大端部速度为1.02 m/s，大于公式（6）计算的滑水临界速度。其他工况计算结果也表明，滑动过程中出现过滑水现象。这也是海底滑坡土体可以在较小地形角度下滑动较大距离的原因之一。

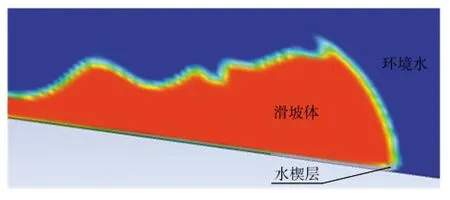
图10　T=1.5 s时体积分数云图（粘土含量28.7%，初始速度1 m/s）

3.3.2混水软化效应

滑坡体在运动过程除了因扰动强度降低之外，环境水的混入也导致了强度降低、流动性加强。混水主要通过两种方式，一种是滑水时滑坡体端部下部水楔的不断混入，另外滑坡体端部受到拉裂等作用也使水不断混入。目前对于上述软化过程（真实状态下海底滑坡从启动到最终的停止，更是一个非常复杂的变化过程），还很难进行准确的力学模型描述。为了分析强度降低对海底滑坡运动的影响，这里进行理想化的假设，只考虑屈服抗剪强度的变化对运动距离的影响。以粘土含量为28.7%的工况为例，其初始屈服抗剪强度约为108.7 Pa，对其逐步降低进行求解。图11为对应不同的最大运移距离。可以看出，强度的降低能够大幅提升运动距离。而真实状态下海底滑坡土体的强度降低，是一个不断累计发生的过程，而强度降低导致的流动性增强，又会进一步满足滑坡体滑水所需的速度条件，这也是海底滑坡大距离运移的主要原因。另外，当弱化后的屈服抗剪强度分别等于粘土含量为15%和20%的屈服抗剪强度时，弱化后的最大运移距离仍然小于他们对应的最大运移距离，粘土含量越低，差值越大。上述表明，采用塑性流体模拟海底滑坡运动时，要同时考虑其屈服强度和粘滞系数降低的影响，特别是滑动后期滑坡体表现为较明显的流体特性阶段。

图11　不同屈服强度下泥浆的最大运移距离

4　结论

本文主要基于小尺度的数值模拟讨论海底滑坡的一般性规律。欧拉-欧拉两相流模型能够通过计算滑坡体与环境水的相互作用实现对“滑水”现象的捕捉，可较好的模拟海底滑坡的运动情况。地形角度、材料组成、初始动能以及滑坡规模都对最终运动距离有较大影响。通过与无水条件下的模拟结果对比，小角度地形下海底滑坡的运动距离相对较大，同时海底滑坡在运动过程中因扰动和环境水混入而导致的强度降低能够显著提高其运动距离。

实际的海底滑坡过程是一个非常复杂的过程，目前欧拉-欧拉两相流模型还很难全面考虑海底滑坡在运动过程中因扰动和混水而导致的强度降低情况，同时也不能反映滑坡体内砂的单独沉积情况。原因除了模型本身的理论限制外，对于上述现象的理论、实验研究也有待于进一步开展。

De Blasio F V,Elverhoi A,Issler D,et al,2005.On the dynamics of subaqueous clay rich gravity mass flows-the giant Storegga slide, Norway.Marine and Petroleum Geology,22(1):179-186.

De Blasio F V,Engvik L,Harbitz C B,et al,2004.Hydroplaning and submarine debris flows.Journal of Geophysical Research,109, C01002.

Gauer P,ElverhØi A,Issler D,et al,2006.On numerical simulations of subaqueous slides:Back-calculations of laboratory experiments. Norwegian Journal of Geology,86:295-300.

Harbitz C B,Parker G,ElverhØi A,et al,2003.Hydroplaning of subaqueous debris flows and glide blocks analytical solutions and discussion.Journal of Geophysical Research,108(B7):107-137.

Ilstad T,D E Blasio F V,ElverhØi A,et al,2004a.On the frontal dynamics and morphology of submarine debris flows.Marine Geology,213(1-4):481-497.

Ilstad T,Elverhbi A,Issler D,et al,2004b.Subaqueous debris flow behaviour and its dependence on the sand/clay ratio:a laboratory study using particle tracking.Marine Geology,213:415-438.

Imran J,Harff P,Parker G,2001a.A numerical model of submarine debris flow with graphical user interface.Computers Geoscience, 227:721-733.

Imran J,Parker G,Locat J,et al,2001b.1D numerical model of muddy subaqueous and subaerial debris flows.Journal of Hydraulic Engineering,127(11):959-968.

L'Heureux J S,Vanneste M,Rise L,et al,2013.Stability mobility and failure mechanism for landslides at the upper continental slope off Vesterålen,Norway,Marine Geology,346:192-207.

Locat J,Lee H J,2002.Submarine landslides:Advances and challenges. Canadian Geotechnical Journal,39(1):193-212.

Mohrig D,Whipple K X,Hondzo M,et al,1998.Hydroplaning of subaqueous debris flows.Geological Society of America Bulletin, 110(3):387-394.

Mosher D C,Moscardelli L,Shipp R C,et al,2010.Submarine mass movements and their consequences.Mosher D C,Moscardelli L, Shipp R C,et al,eds,Submarine mass movements and their consequences,Springer,Berlin,1-8.

Nadim F,Locat J,2005.Risk assessment for submarine slides.Hunger O, Fell R,Couture R,et al,eds,International conference for landslide risk,Aa Balkema:Vancouver,321-334.

Parker E J,Traverso C,Moore R,et al,2008.Evaluation of landslide impact on deepwater submarine pipelines.OTC.Waves of change. Curran Associates,New York,OTC19459.

Randolph M,Seo D,White D J,2010.Parametric Solutions for Slide Impact on Pipelines,Journal of Geotechnical and Geoenvironmental Engineering,136(7):940-949.

Wright S G,Hu Hongrui.2007.Risk assessment for submarine slope stability-hydroplaning.Final project report prepared for the Minerals Management Service under the MMS/OTRC cooperative research agreement 1435-01-04-CA-35515 task order 39323. Austin:The University of Texas.

Xiu Z X,Liu L J,Xie Q H,et al,2015.Runout prediction and dynamic characteristic analysis of potential submarine landslide in Liwan 3-1 gas field.Acta oceanologica sinica,34(7):116-122.

Yuan F,Li L L,Guo Z,et al,2015.Landslide impact on submarine pipelines:analytical and numerical analysis,Journal of Engineering Mechanics,ASCE,141(2):04014109.

胡光海，2011.东海陆坡海底滑坡识别及致滑因素影响研究.青岛：中国海洋大学.

刘保华，李西双，赵月霞，等，2005.冲绳海槽西部陆坡碎屑沉积物的搬运方式：滑塌和重力流.海洋与湖沼，36（1）：1-9.

刘杜娟，潘国富，叶银灿，2010.东海陆架典型海洋灾害地质因素及其声反射特征.海洋通报，29（6）：664-668.

刘乐军，傅命佐，李家钢，等，2014.荔湾3-1气田海底管道深水段地质灾害特征.海洋科学进展，32（2）：162-174.

彭俊，陈沈良，陈一强，等，2014.黄河三角洲侵蚀性岸段水下岸坡地质灾害及其空间分布.海洋通报，33（1）：1-6.

吴时国，陈珊珊，王志君，等，2008.大陆边缘深水区海底滑坡及其不稳定性风险评估.现代地质，22（3）：430-437.

（本文编辑：袁泽轶）

Sensitivity analysis of submarine landslide mass movement based on the small-scale numerical model

XIU Zong-xiang1,2,LIU Le-jun1,XIE Qiu-hong1,LI Xi-shuang1, HU Guang-hai1,LI Jia-gang3,ZHAO Qiang1
（1.First Institute of Oceanography,SOA,Qingdao 266061,China;2.State Key Laboratory of Coastal and OffshoreEngineering,Dalian 116024,China;3.CNOOC Research Institute,Beijing,100027,China）

Study of submarine landslide movement characteristics is the basis for the understanding and prevention of the landslide geological hazard in the continental slope area.The small-scale numerical model of submarine landslide is established based on the Non-Newtonian Eulerian-Eulerian two-phase model.The validity of the established model is verified through the comparison with experiment data and the BING simulated result.The general movement behaviors of submarine landslide are then studied,and the simulated results are also compared with those without water.The result shows that the ambient water can lead the occurrence of hydroplaning phenomenon,which mainly can extend the running time of submarine landslide,and make a larger run-out distance.But the calculated maximum front peak velocity of submarine landslide is smaller than that without water.Soil composition,topographic slope,initial velocity and initial thickness play important roles in the submarine landslide run-out distance.The continuing decrease of yield strength and viscosity resulted by the soil disturbance and the incorporation of water during the movement process are the main reason for the larger run-out distance of submarine landslide.

submarine landslide;Eulerian-Eulerian two-phase model;Herschel-Bulkley model;hydroplaning;soften

P694

A

1001-6932（2016）04-0380-06

10.11840/j.issn.1001-6392.2016.04.003

2015-04-02；

2015-08-27

国家自然科学基金青年基金项目（41206058）；国家科技重大专项子课题（2011ZX05056-001-02）；中央级公益性科研院所基本科研业务费专项资金项目（2013a25）；大连理工大学海岸和近海工程国家重点实验室开放基金项目（LP1514）

修宗祥（1982-），男，博士，副研究员，主要从事海洋工程地质灾害风险评价研究。电子邮箱：xiuzongxiang@163.com

解秋红（1982-），女，博士，助理研究员。电子邮箱：xqh@fio.org.cn。