基于KPLS的滚动轴承装配质量预测

万方华, 王晓琪, 张　洪, 丁诗泳, 陈建国, 王通德, 潘文斌

(1. 江苏南瑞恒驰电气装备有限公司 江苏 无锡 214000；2.中国电力科学研究院 江苏 无锡 214000；3.江南大学 机械工程学院 江苏 无锡 214122)



基于KPLS的滚动轴承装配质量预测

万方华1, 王晓琪2, 张洪3, 丁诗泳3, 陈建国1, 王通德1, 潘文斌1

(1. 江苏南瑞恒驰电气装备有限公司 江苏 无锡 214000；2.中国电力科学研究院 江苏 无锡 214000；3.江南大学 机械工程学院 江苏 无锡 214122)

轴承的装配质量在机械运行过程中起到十分关键的作用。为了预测轴承的装配质量，建立了能够准确表征轴承特性与零件几何要素间关系的数学模型，对轴承产品装配质量进行预测。结果表明采用核偏最小二乘回归法(kernel partial least squares,KPLS)对轴承的装配质量进行预测，克服了实际生产中非线性因素对预测模型的不利影响，具有很好的预测精度，为轴承的精准制造提供了帮助，具有十分重要的意义。

轴承； 装配质量； 预测； 回归

滚动轴承是各类机器中广泛应用的重要机械部件，运转精度较高。主要由滚动体、保持架、内外套圈组成，它们的几何精度和装配质量直接影响了轴承的运转性能。建立轴承装配质量与各几何要素之间的数据驱动模型，通过此模型，就能使轴承在装配中预测和控制其装配质量精度，以降低生产成本，提高生产效率，是目前实现智能制造的一个的研究方向。

轴承的装配质量控制研究中，宋小兵[1]研究开发了基于六西格玛的质量管理信息系统，并在微型轴承企业装配中验证了使用该系统进行质量管理的可行性。叶玉婷[2]使用SVM方法，通过学习，构造出决策函数，来对轴承进行质量控制。钟懿[3]设计了一套适用于质量监控的编码体系。研究出了基于OPC技术的质量监控交互系统。张越迪[4]采用SPC技术，利用休哈特控制图对轴承的质量控制方法进行了研究。许丽等[5]采用主元分析(PCA)方法研究了轴承质量控制方法。苗学文等[6]运用BP网络，建立了特征向量与状态寿命之间的映射。

以上的方法是对轴承制造中的工艺要素控制，而无法在轴承装配前对其装配质量进行预测。本文根据变量之间的非线性关系特点，研究、建立了基于核偏最小二乘回归(KPLS)方法的数学模型，对轴承装配质量进行控制与预测。

1　轴承影响因素分析

滚动轴承在旋转中的振动值，是影响设备运行的重要因素之一，在诸多能引起轴承振动的的因素中，内外圈沟道的圆度、波纹度、沟位差、尺寸偏差，内圈内径，钢球尺寸偏差等参数对轴承影响较大[7-9]。图1为某轴承内、外圈沟道的波纹度，从图中可以看出，轴承内、外圈沟道波纹度之间存在着一定的相关关系。并且这些因素与控制量之间还存在着非线性的关系，核偏最小二乘回归法(KPLS)根据因素与控制量之间的非线性关系，通过测量数据，采用偏最小二乘回归的方法，去除了自变量间的相关性的，建立了基于数据驱动的数学模型，预测轴承装配后的装配质量，实现轴承质量在线控制。

图1　部分数据波纹度散点图

2　KPCA方法

2.1基本原理

2.2核函数的概念

核函数[7]的名称来源于积分算子理论，Mereer定理从理论上解决了核函数的确定及其特性。x经过非线性映射后，在高维映射空间中得到一个列向量Φ。如在原始空间存在一个函数Ki,j=K[x(i),x(j)],满足K[x(i),x(j)]=ΦT(i)Φ(j),ΦT(i)Φ(j)为高维空间中的Φ(i)与Φ(j)的内积(i,j=1,2,…,n),则称K[x(i),x(j)]为核函数。如高维空间的矩阵K=ΦΦT中的每一个元素ΦT(i)Φ(j)均用核函数K[x(i),x(j)]表示，则称矩阵K为核函数矩阵,简称核矩阵。

2.3核偏最小二乘法

对K和Kt在高维空间进行中心化处理：

(2)

(3)

式中，I为n维单位矩阵；ln和lt为元素为1，长度分别为n和nt的向量。

建立回归模型后，计算回归数据的拟合值为

(4)

测试数据的预测值为

(5)

3　KPCA的应用

3.1变量选择及数据预处理

以61800-2Z型滚动轴承为研究对象，选择与轴承振动相关的10个参数，依次分别是x1、x2、x3、x4、x5、x6、x7、x8、x9、x10，其表示的含义如表1所示。建立y-振动值(dB)与以上10个参数之间的回归方程。

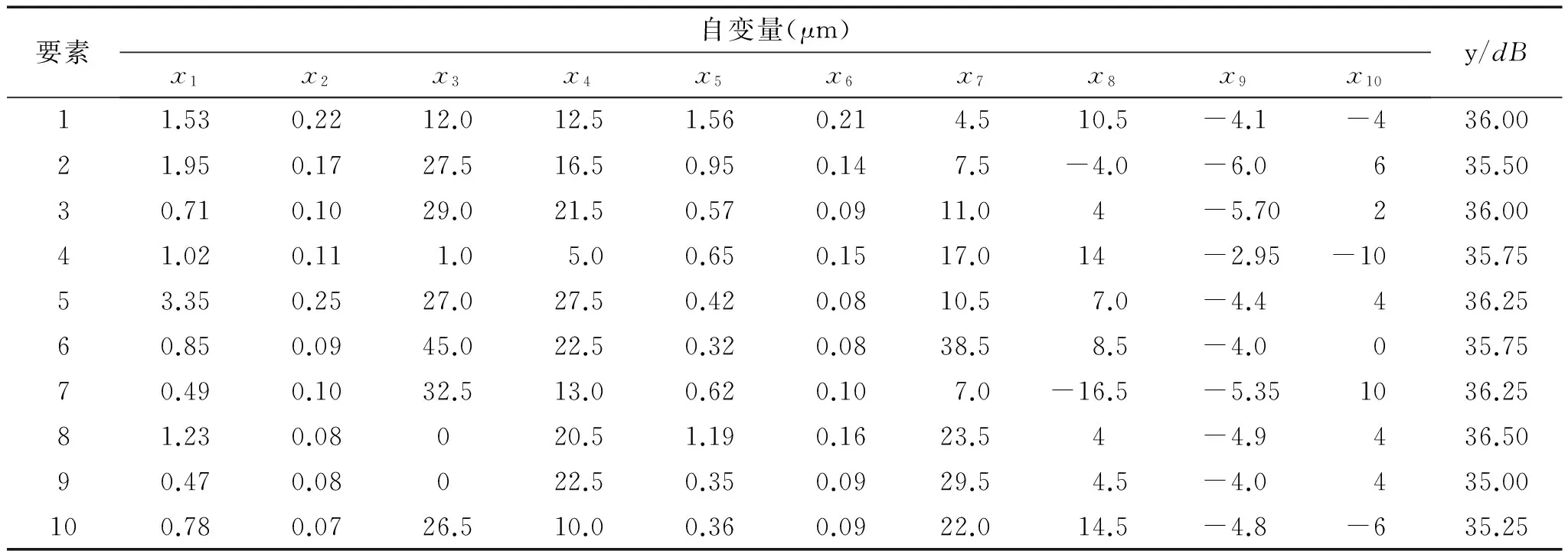
表2　部分原始数据

样本数据的标准化处理按式(6)进行。

(6)

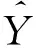
(7)

其中，j=1,2,…,q。

Y=(y1,…,yq)的预测残差平方和为

2组原发性高血压患者治疗后的血压水平均较治疗前降低,其中实验组减低程度优于对照组(P<0.05)。如表2:

(8)

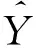
(9)

Y=(y1,…,yq)的预测残差平方和为

(10)

定义交叉有效性为

(11)

在完成样本数据预处理和模型参数选择之后，就可以通过式(4)拟合回归模型，通过式(5)对测试数据进行预测。

通过KPLS得出的结果为标准化以后的值，需通过反标准化还原得到最终的预测值，反标准化按照式(12)进行，即原始数据标准化的反过程。

(12)

3.2研究结果及分析

随机抽取了15组轴承，测量其自变量x1～x15，得出y，并与实际测量值进行对比，来对模型精确度进行验证。具体见表3。

表3　实测值与预测值对比

为清晰对比，作出实测值与预测值之间的散点图，如图2所示。

图2　实测值与预测值的散点图

由表3和图2可以清楚地看出，用KPLS来拟合的轴承的振动值的误差较小，所以，可以采用KPLS来对轴承振动值进行预测。

4　结语

经过生产应用证明，采用KPLS建立的轴承装配质量的预测模型，通过轴承零件的几何精度数据可以更有效地预测轴承的装配质量。此方法的应用，对提高轴承的旋转性能，增加使用寿命，降低生产成本具有重要意义。

[1]宋小兵.面向微型轴承装配过程的六西格玛质量管理信息系统研究[D].杭州：浙江大学,2003.

SONG Xiaobing. Study on six Sigma quality information system for miniature bearing sssembling process[D].Hangzhou: Zhejiang University,2003.

[2]叶玉婷.滚动轴承质量检测数据库管理系统的设计与实现[D]武汉：华中科技大学,2013.

YE Yuting. Design and Implementation of Bearing Quality Detection Database Management System[D]. Wuhan: Huazhong University of Science and Technology,2013.

[3]钟懿.面向轴承制造过程的全面质量监控系统研究与开发[D].杭州：浙江大学,2007.

ZHONG Yi. Research and Development of Total Quality Monitoring System for Manufacturing Process of Bearing[D].Hangzhou: Zhejiang University,2007.

[4]张越迪.面向轴承制造过程中的工序质量控制研究[D].重庆：重庆大学，2012

ZHANG Yuedi. Study on Process Quality Control for Manufacturing Process of Bearing[D]. Chongqing: Chongqing University,2012.

[5]许丽,张进明,张广明,等.基于PCA的滚动轴承故障检测方法[J].计算机仿真，2010,27(6):325-329.

XU Li,ZHANG Jinming,ZHANG Guangming, et al. A Method of Rolling Bearing Fault Detection Based on PCA[J]. Computer Simulation, 2010,27(6):325-329.

[6]苗学问,洪杰,马艳红.基于小波包和BP网络的滚动轴承状态寿命模型[J].北京航空航天大学学报,2009,10: 1161-1165.

MIAO Xuewen,HONG Jie,MA Yanhong .Grade-life model based on wavelet package and BP network for rolling bearing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009,10: 1161-1165.

[7]赵铭,付丽霞. 表面粗糙度对深沟球轴承振动值的影响[J].轴承，2004(5):33-34.

ZHAO Ming,FU Lixia .Effects of surface roughness on vibration of deep groove ball bearings[J].Bearing, 2004(5):33-34.

[8]赵联春,马家驹,马纯青,等.润滑对球轴承振动特性的影响[J].摩擦学学报，2003,23(5)：421-425.

ZHAO Lianchun,MA Jiaju,MA Chunqing, et al. Effect of Lubrication on the Vibration Characteristics of Ball Bearings[J]. Tribology，2003,23(5)：421-425.

[9]王哲,胥利.沟道形状误差对深沟球轴承振动和噪音的影响[J].哈尔滨轴承，2009,30(4)：23-24.

WANG Zhe,XU Li. Influence of groove shape error on vibration and noise of deep groove ball bearing[J]. Journal of Harbin Bearing，2009,30(4)：23-24.

[10]陈南祥,曹连海,李梅,等.偏最小二乘回归神经网络的矿坑涌水量预测[J].吉林大学学报,2005,35(6):766-770.

CHEN Nanxiang,CAO Lianhai,LI Mei, et al. Forecasting Water Yield of Mine with the Partial Least Square Method and Neural Network[J]. Journal of Jilin University,2005,35(6):766-770.

Rolling Bearing Assembly Quality Forecasting Based on Kernel Partial Least Squares

WAN Fanghua1，WANG Xiaoqi2, ZHANG Hong3，DING Shiyong3，CHEN Jianguo1，WANG Tongde1，PAN Wenbin1

(1. Wuxi Hengchi Electric Apparatus Manufacturing Co., Ltd, Wuxi 214000, China; 2. State Grid Electric Power Research Institute, Wuxi 214000, China; 3.School of Mechanical Engineering，Jiangnan University, Wuxi 214122, China)

The assembly quality of bearing plays a vital role in the mechanical operation process. In order to predict the quality of the bearing assembly, a mathematical model of accurately formulating relations between bearing characteristics and geometric components is proposed to predict assembly quality of bearings, which is very important to quality control of bearings. Using the kernel partial least square method to predict bearing assembly quality can overcome the adverse effects of the nonlinear factors. Research shows that the method results in a better accuracy and is helpful to bearing precision manufacturing.

bearing; assembly quality; predict; regression

2015- 02- 02

国家自然科学基金资助项目(51107053)

万方华(1968-)男，湖北省人，高级工程师，硕士,主要研究方向为高压电器产品的设计与制造.

10.3969/j.issn.1007- 7375.2016.04.020

TH 161+.7

A

1007-7375(2016)04- 0136- 04