“机器换人”财政补贴方式和补贴策略优化

孙玉卫， 张智聪

(1. 华南理工大学 工商管理学院， 广东 广州 510641； 2.东莞理工学院 工业工程系， 广东 东莞 523808)



“机器换人”财政补贴方式和补贴策略优化

孙玉卫1,2， 张智聪2

(1. 华南理工大学 工商管理学院， 广东 广州 510641； 2.东莞理工学院 工业工程系， 广东 东莞 523808)

基于博弈论方法，研究了“机器换人”的两种财政补贴方式下政府补贴资金的最优分配及其效率。首先，分别在定比和定额两种补贴方式下建立了“政府-设备供应商-设备应用企业”三方序贯博弈模型，从而得出了在两种补贴方式下政府补贴资金在供应链成员即设备供应商和应用企业之间的最佳分配方案；然后在最优分配方案下对两种补贴的影响和补贴资金使用效率进行了分析和比较；最后，针对两种补贴方式的特点提出了“机器换人”财政补贴建议。研究表明，定比补贴下政府补贴资金在设备供应商和应用企业之间的最佳分配方案是将补贴全部分配给应用企业，而在定额补贴下政府可以将补贴以任意比例在设备供应商和应用企业之间分配；并且定额补贴的资金使用效率高于定比补贴。

供应链； 机器换人； 补贴方式及分配决策； 政企博弈； 资金使用效率

随着劳动力价格的上涨，中国制造业的人口红利正在不断消失。以自动化、智能化装备提升传统产业竞争力，推动技术红利替代人口红利，成为解决企业“用工贵”和“用工荒”难题以及促进中国制造业转型升级的必然选择。在这种背景下，近年长三角和珠三角的传统制造企业兴起了“机器换人”，引进自动化的智能装备进行技术改造升级。为促进制造业企业“机器换人”，这些地区政府部门纷纷出台“机器换人”行动计划及相关扶持政策。本文研究的内容是政府针对企业购买自动化设备所进行的财政补贴。财政补贴的一种实现方式是按照设备价格水平的一定比例进行补贴，本文将其称为“定比补贴”。与“定比补贴”相对应的一种补贴方式就是对单台(套)设备进行固定额度的资金补贴，本文称之为“定额补贴”。无论是定比补贴还是定额补贴，政府相关部门都将会面临对“谁”补贴能最大程度促进“机器换人”实施的问题，或是对 “机器换人”应用企业补贴，或是对自动化设备供应商补贴，亦或是按照一定的比例将补贴分配给应用企业和供应商。因此，这里面临的两个问题是政府补贴如何在应用企业和设备供应商之间分配能发挥最大激励作用，以及定比补贴和定额补贴两种补贴方式孰优孰劣。

目前尚没有对“机器换人”财政补贴方式和补贴策略的研究；但在低碳或再制造等背景下研究相关问题时，有些文献对政府补贴进行了考察。根据补贴方式不同可将相关文献分为两类。一类是政府按照价格水平、绿色水平或减排水平的一定比例等对供应链上的成员进行补贴[1-6]。在此类文献中，政府补贴对象是消费者[1-2]，有些则是生产制造商[3-5]，有些则是制造商和零售商两者[6]。另一类是政府对供应链成员进行固定额度的补贴[7-15]。在该类文献中，政府的补贴对象是消费者[7-8]，有些则是生产制造商或再制造商[9-12]，有些则是制造商和再制造商两者[13]，亦或是制造商和零售商两者[14-15]。以上文献均就一种补贴方式进行考察，缺乏两种不同补贴方式效率的比较以及政府补贴在供应链成员之间的最优分配。本文在政府补贴促进制造业企业“机器换人”的实践背景下，考察在定比和定额两种补贴方式下政府补贴资金在设备供应商和设备应用企业之间的最优分配，然后在最优分配方案下分析并比较两种补贴的资金使用效率。

1　政企博弈模型

1.1模型描述

不考虑设备供应商内部竞争即市场上一个设备供应商提供设备给应用企业，则设备供应商与设备应用企业(制造业企业)构成一简单供应链。而政府部门则在定比补贴或定额补贴下将补贴资金分配给设备供应商和应用企业，从而促进“机器换人”的实施。那么，政府部门、设备供应商和应用企业三者之间的互动关系可以用序贯博弈表示。在博弈中，设备应用企业的目标是以低于预期的价格购得设备，在政府部门和设备供应商决策后作出是否购买的决策；设备供应商的目标是利润最大化，在政府部门决策后作出设备价格决策，假设其面临的市场需求为q=a-bp，其中a表示市场潜在容量，p表示价格，b是价格系数，并假设每台设备成本为c，则a>bc(保证市场存在)；而政府的补贴目标是“设备应用数量”最大化和“单台(套)设备平均剩余”最大化，在三者中首先作出决策。“设备应用数量”是指所有“机器换人”应用企业所购买设备的总数量； “单台(套)设备剩余”是指设备购买者愿意对单台(套)设备支付的最高价格与购买该设备所支付实际价格的差额。而“单台(套)设备平均剩余”等于所有被应用企业购买的设备剩余之和与设备数量的商。显然，“设备应用数量”越大，则很大程度上表示参与“机器换人”的企业越多；而“单台设备的平均剩余”越大，则表示“机器换人”应用企业购买单台(套)设备所付出的平均成本越低。因此，本文将政府的补贴目标定为“设备应用数量”最大化和“单台(套)设备平均剩余”最大化。

在定比补贴情况下，记设备价格为p1，销量为q1，设备供应商利润为π1，单台(套)设备平均剩余为s1。政府按照设备价格的一定比例η(η1+η2=η，0<η<1) 进行补贴，即按照设备价格的某一比例η1对设备供应商补贴，按照设备价格的某一比例η2对应用企业补贴；则对于每台设备，供应商可获补贴p1η1，应用企业可获补贴p1η2。

在定额补贴情况下，记设备价格为p2，销量为q2，设备供应商利润为π2，单台(套)设备平均剩余为s2。政府部门对每台(套)设备的补贴为某一确定额m(m>0)，将该定额的一部分mβ1分配给供应商，一部分mβ2分配给应用企业，其中0<β1,β2<1(β1+β2=1)；则对于每一台设备，设备供应商可获补贴mβ1，应用企业可获补贴mβ2。

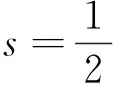
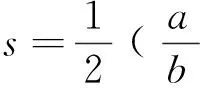
而在定比补贴与定额补贴下每台(套)设备剩余分别增加p1η2、mβ2，所以两种补贴下的单台(套)设备平均剩余如下所示。

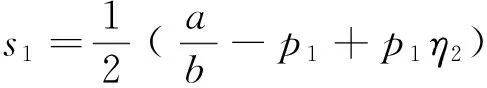
(1)

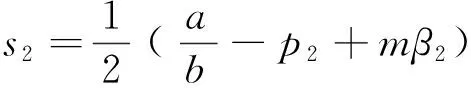
(2)

1.2模型建立和求解

下面以定比补贴和定额补贴为序分别建政府、设备供应商以及应用企业之间的博弈模型。

1.2.1定比补贴下的政企博弈

在定比补贴情况下，存在一个三阶段博弈，其顺序为：政府在定比补贴下制定补贴策略，设备供应商作出价格决策，应用企业作出购买决策。下面采用逆序解法考察三者之间的博弈过程。

博弈第3步，每个应用企业均会对所要购买的设备有预期的最高可接受价格。若设备实际价格高于预期价格则放弃购买；若设备实际价格低于预期价格则购买设备。在政府部门定比补贴下，所有作出购买决策的应用企业对设备的需求量表现为需求函数q1=a-bp1(1-η2)。

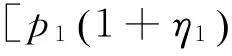
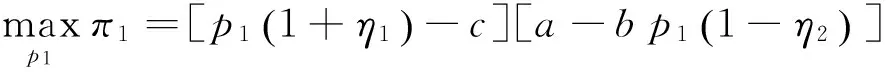
(3)

解式(3)可得设备供应商的最优价格决策以及最优利润：

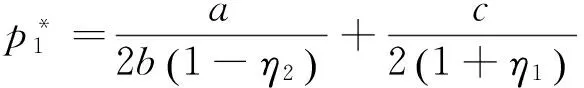
(4)

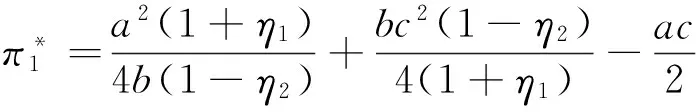
(5)

与此同时，作出购买决策的应用企业其所购买设备数量的最优取值也进一步确定，如式(6)所示，单台(套)设备平均剩余的最优取值如式(7)所示。

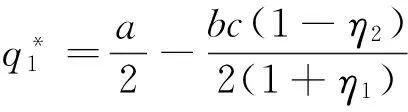
(6)

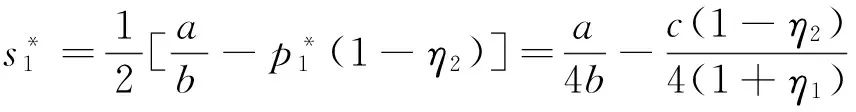
(7)

博弈第1步，政府分别以设备应用数量最大化和单台(套)设备平均剩余最大化为补贴目标制定最优补贴策略即确定η1和η2的取值(η1+η2=η)。

为简化运算，将η1+η2=η代入式(6)和式(7)消去η2可分别得到式(8)和式(9)。

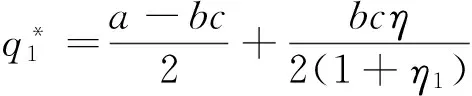
(8)

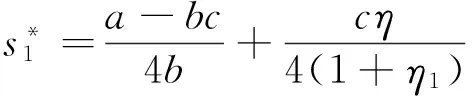
(9)

以最大化设备应用数量和最大化单台(套)设备平均剩余为补贴目标，即：

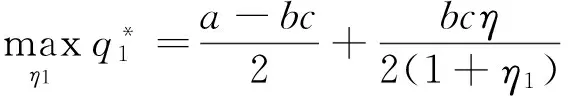
(10)

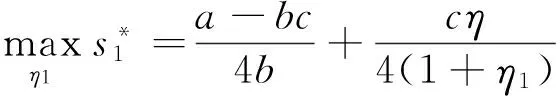
(11)

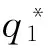
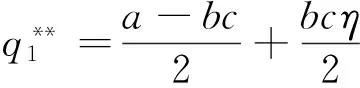
(12)

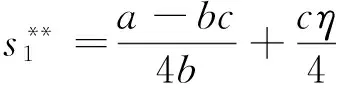
(13)

由此可知，在定比补贴下，政府补贴资金全部分配给应用企业可以同时使得政府两个补贴目标最大化，即在定比补贴下政府补贴资金的最优分配方案是将资金全部配给应用企业(η1=0，η2=η)。此时，设备应用数量、单台(套)设备平均剩余、设备价格和供应商利润二次优化取值分别如式(12)～(15)所示。

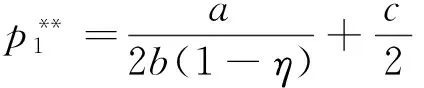
(14)

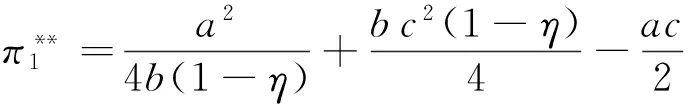
(15)

1.2.2定额补贴下的政企博弈

在定额补贴情况下，存在与定比补贴下相同的三阶段博弈，不再赘述。下面采用逆序解法考察三者之间的博弈过程。

博弈第3步，设备应用企业的目标是以低于预期的价格购得设备。在政府定额补贴下，所有作出购买决策的应用企业对设备的需求量表现为需求函数q2=a-b(p2-mβ2)。

博弈第2步，设备供应商以其利润最大化为决策目标制定设备价格，其决策目标函数如式(16)所示。其中(p2-c+mβ1)为设备供应商获得政府价格补贴定额mβ1后单台(套)设备的利润。

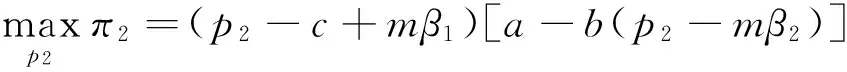
(16)

解式(16)可得设备供应商的最优价格决策以及最优利润：

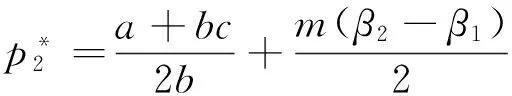
(17)

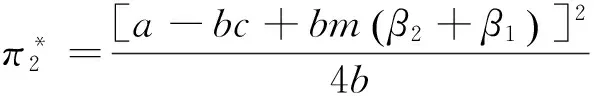
(18)

与此同时，作出购买决策的应用企业所购买设备数量的最优取值也进一步确定如式(19)所示，单台(套)设备平均剩余的最优取值如式(20)所示。

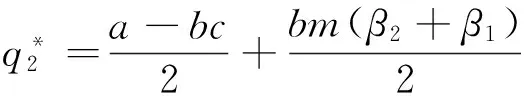
(19)

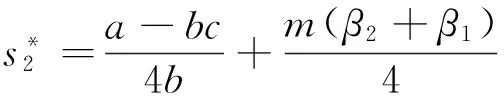
(20)

博弈第1步，政府分别以设备应用数量最大化和单台(套)设备平均剩余最大化为补贴目标制定最优补贴策略即确定β1和β2的取值。观察式(19)和式(20)可以得知：设备应用数量和平均剩余均与β1、β2各自取值无关，而只与两者之和相关。因此，在定额补贴下，政府部门可将补贴定额m以任一比例在设备供应商和应用企业之间分配。将β1+β2=1代入式(18)～(20)，可以得到供应商利润、设备应用数量以及应用企业剩余的二次优化取值分别如式(21)～式(23)所示。而此时设备价格的取值与β1、β2取值相关如式(24)所示。

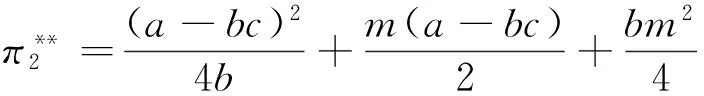
(21)

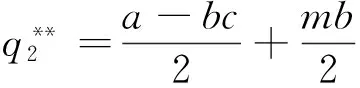
(22)

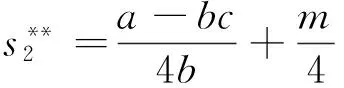
(23)

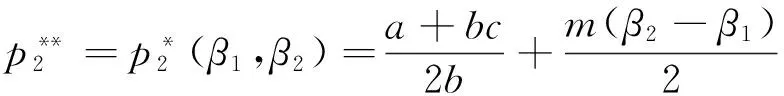
(24)

结论1在定比补贴下，政府部门补贴资金的最优分配方案是将补贴全部分配给应用企业。而在定额补贴下，补贴定额m在设备供应商和应用企业间如何分配并不会影响补贴效果，即政府部门将补贴定额m以任一比例在设备供应商和应用企业之间分配均能实现补贴目标的最优化。

2　补贴影响分析

本节将考察，在最优资金分配方案下，2种补贴对政府、设备供应商以及“机器换人”应用企业三方产生的影响。

2.1定比补贴影响分析

在定比补贴的情况下，政府补贴对政府、设备供应商以及“机器换人”应用企业的影响分别如性质1～3所示。

2.1.1政府所付出补贴资金总额

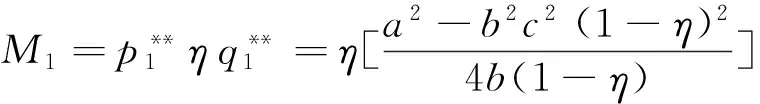
(25)

性质1在定比补贴下，随着比例η的增大，政府所付出的补贴资金总额M1增大并且增加速度越来越快，即dM1/dη>0且d2M1/dη2>0。

证明因为a>bc且0<η<1，

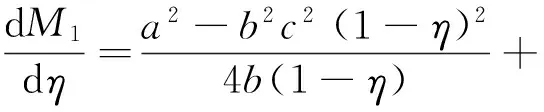
2.1.2供应商定价和利润情况

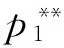
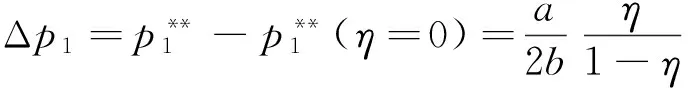
(26)

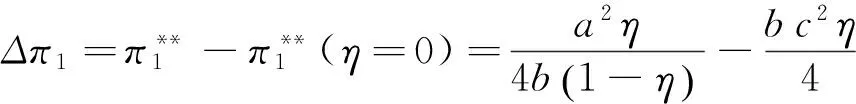
(27)

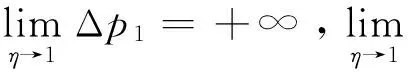
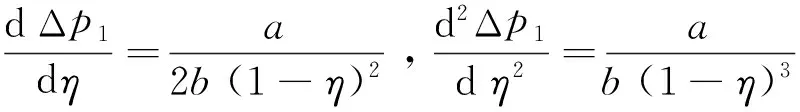
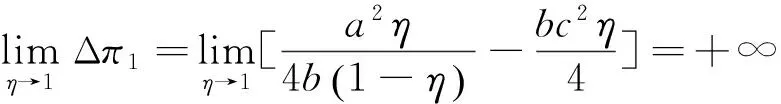
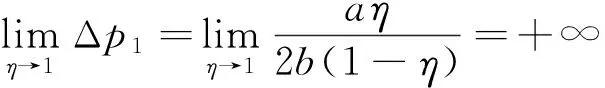
由性质2可知，设备价格增长量随补贴比例η的变化如图1所示。

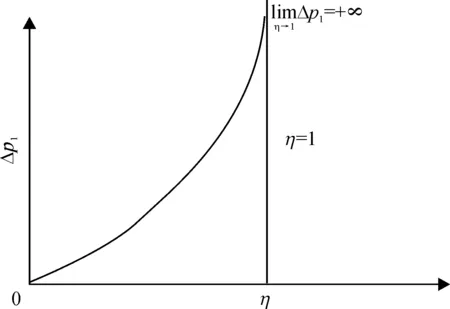
图1　价格增长量Δp1与补贴比例η的关系

2.1.3应用企业设备购买量和剩余情况

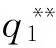
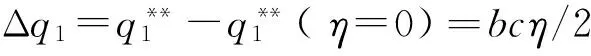
(28)

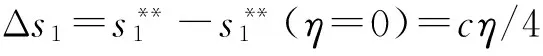
(29)

性质3在政府部门实施定比补贴的情况下，设备应用增加量Δq1、单台(套)设备平均剩余增加量Δs1与补贴比例η成正比。(性质3显然成立，证明省略)

结论2在定比补贴下，随着政府补贴比例的增大，政府所付出的补贴总额、设备供应商利润以及设备定价逐渐增大，并且增大速度在加快，而设备应用数量增加量和单台设备平均剩余增长量在匀速增长。

2.2定额补贴影响分析

在定额补贴的情况下，政府补贴对政府、设备供应商以及“机器换人”应用企业的影响分别如性质4～6所示。

2.2.1政府所付出补贴资金总额

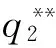
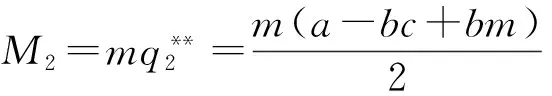
(30)

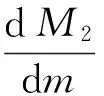
因为M2是关于m的二次多项式且m>0及a>bc，所以性质4显然成立。

2.2.2供应商定价和利润情况

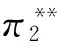
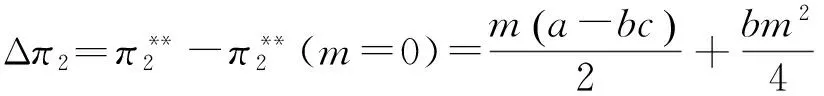
(31)

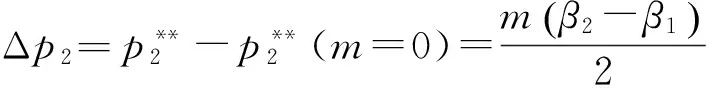
(32)

性质5a在定额补贴下，随着政府补贴定额m的增大，设备供应商的利润增大并且增长速度在加快。(证明同性质4)

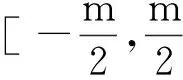
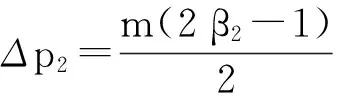
性质5b表明，在定额补贴下，设备价格会出现降低、提高和不变3种情况:1)当β2>β1时，即政府对应用企业的补贴额大于对设备供应商的补贴额时，设备供应商会提高设备价格，此时设备价格变化量与补贴额度m呈正比；2)当β2=β1=0.5时，即政府对应用企业的补贴额等于对设备供应商的补贴额时，设备供应商会保持设备价格不变；3)当β2<β1时，即政府对应用企业的补贴额小于对设备供应商的补贴额时，设备供应商会降低设备价格，此时设备价格变化量与补贴额度m呈反比。

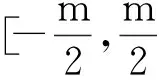
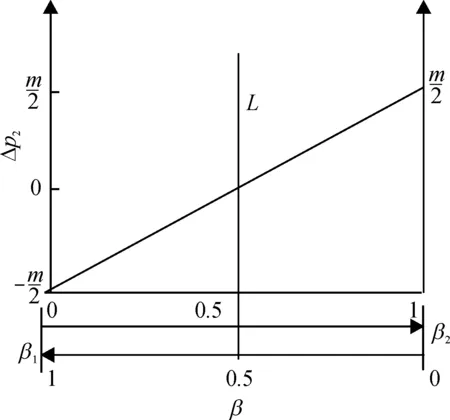
图2　价格变化量Δp2与分配比例β1和β2的关系

2.2.3应用企业设备购买量和剩余情况

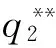
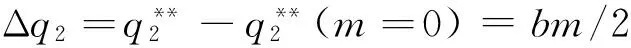
(33)

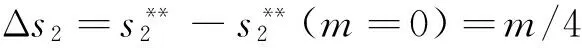
(34)

性质6在政府部门实施定额补贴的情况下，设备应用增加量Δq2、单台(套)设备平均剩余增加量Δs2与补贴定额m成正比。(性质6显然成立，证明省略)。

结论3在定额补贴下，随着政府补贴定额m的增大，政府所付出的补贴总额和设备供应商利润逐渐增大,并且增大速度在加快，而设备应用数量增加量和单台设备平均剩余增长量在匀速增长，设备价格因补贴额m在设备供应商和应用企业之间的分配不同而出现升高、不变和降低3种情况。

3　两种补贴方法的效率

如前文所述，为最大程度促进制造企业实施“机器换人”进行技术改造升级，将政府补贴目标定为设备应用数量最大化和单台(套)设备平均剩余最大化。与政府补贴目标保持一致，下面分别用“设备应用增加量”和“单台(套)设备平均剩余增加量”与补贴资金总额的比值定义两种效率指标对补贴资金使用效率进行考察。

“设备应用增加量”指标(效率指标1)是指单位补贴资金带来的设备应用数量增加；“单台(套)设备平均剩余增加量”(效率指标2)指标是指单位补贴资金带来的单台(套)设备平均剩余增加量。“设备应用数量”指标取值等于设备应用增加总量与所用补贴资金总额之商；“单台(套)设备平均剩余”指标取值等于单台(套)设备平均剩余增加量与所用补贴资金总额之商。

3.1定比补贴下补贴资金使用效率

用e11和e12分别表示在定比补贴下的“设备应用增加量”指标和“单台(套)设备平均剩余增加量”指标取值。在定比补贴的情况下，政府所付出的补贴资金总额M1如式(25)所示，而“设备应用增加量”和“单台(套)设备平均剩余增加量”分别为Δq1和Δs1，其值分别如式(28)和式(29)所示；所以在定比补贴下补贴资金额使用效率e11和e12分别如为

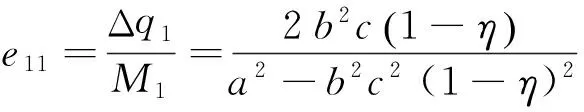
(35)

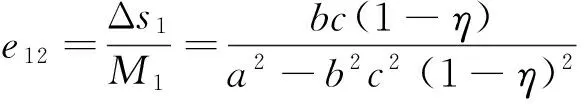
(36)

性质7在定比补贴下，随着政府补贴比例η的增加，补贴资金的使用效率的两种指标e11和e12取值均在减小并且减小速度在减慢，即de11/dη<0，de12/dη<0且d2e11/dη2>0，d2e12/dη2>0；当补贴比例η趋于1时，e11和e12取值趋于0。

证明因为a>bc且0<η<1，所以

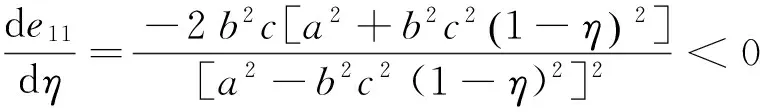
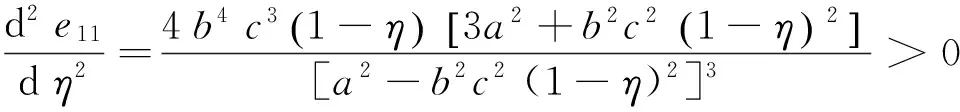
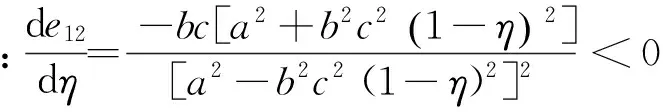
d2e12/dη2=

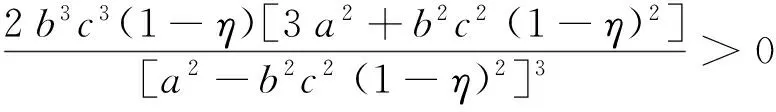
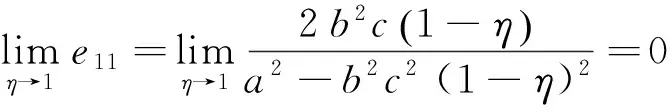
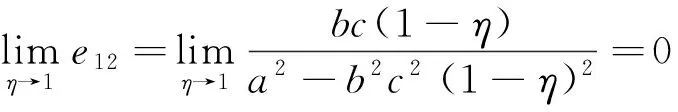
由性质7可知，随着政府补贴比例η的增加，e11和e12的变化趋势分别如图3和图4所示。

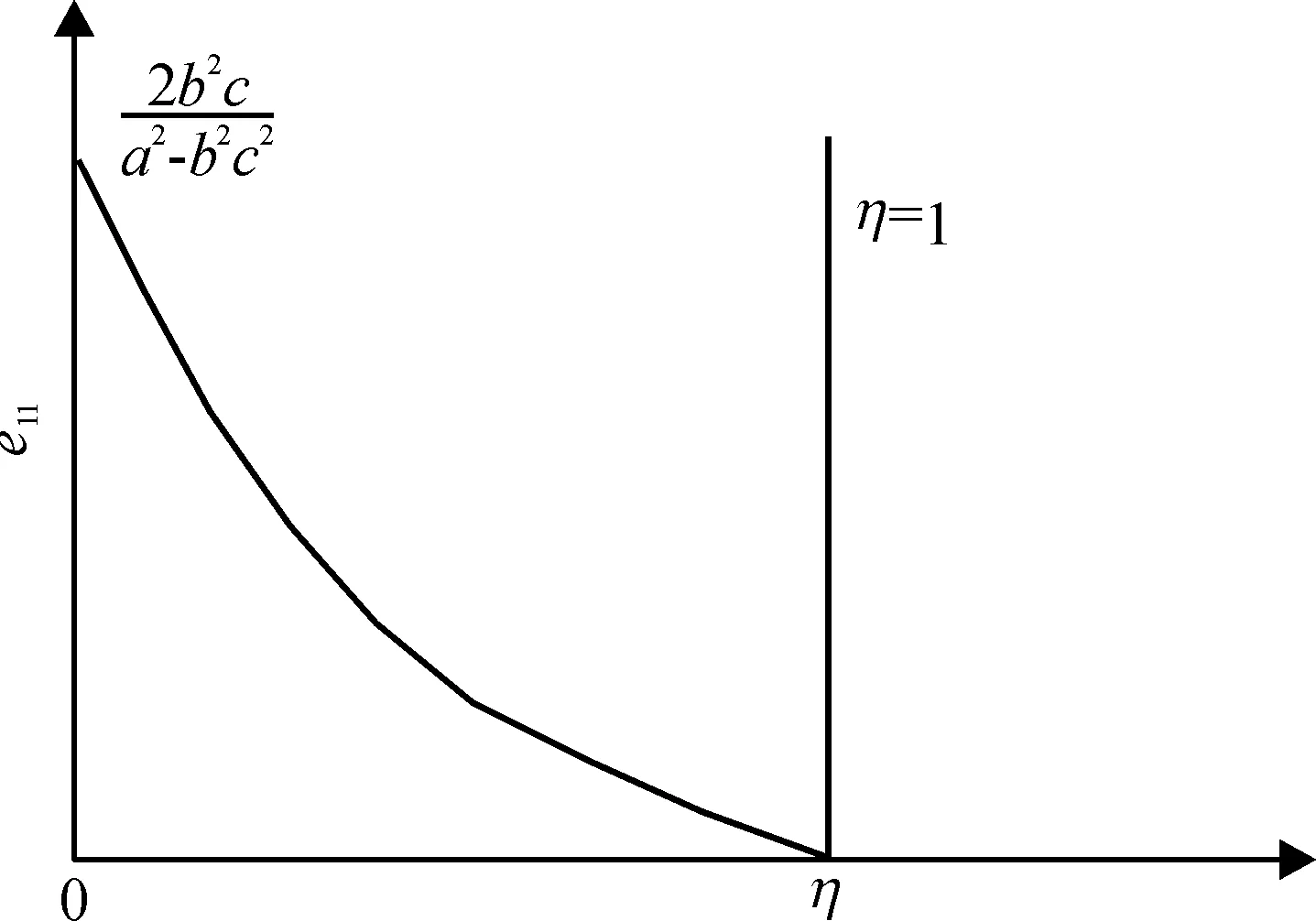
图3　补贴资金使用效率e11与补贴比例η关系

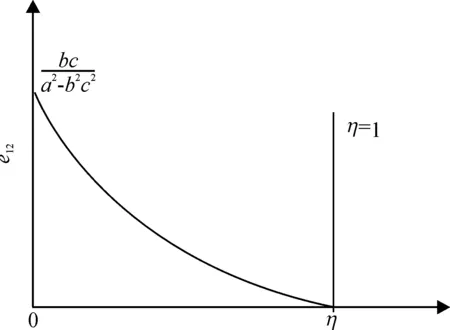
图4　补贴资金使用效率e12与补贴比例η关系

3.2定额补贴下补贴资金使用效率

用e21和e22分别表示在定额补贴下的“设备应用增加量”指标和“单台(套)设备平均剩余增加量”指标。在定额补贴的情况下，政府所付出的补贴资金总额M2如式(30)所示，“设备应用增加量”和“单台(套)平均剩余增加量”分别为Δq2和Δs2，其值分别如式(33)和式(34)所示；所以在定额补贴下补贴资金额使用效率e21和e22分别为：

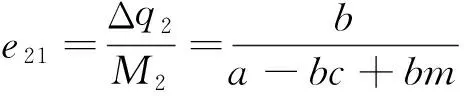
(37)

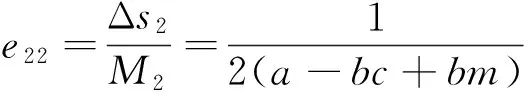
(38)

性质8在定额补贴下，随着政府补贴定额m的增加，补贴资金的使用效率的两种指标e21和e22取值均在减小并且减小速度在减慢，即de21/dm<0，de22/dm<0且d2e21/dm2>0，d2e22/dm2>0；当补贴定额m趋于无穷时，e21和e22取值趋于0。

证明因为de21/dm=-b2/(a-bc+bm)2，de22/dm=-b/2(a-bc+bm)2，所以de21/dm<0，de22/dm<0成立。

d2e21/dm2=2b3/(a-bc+bm)3>0，d2e22/dm2=b2/(a-bc+bm)3>0也显然成立。

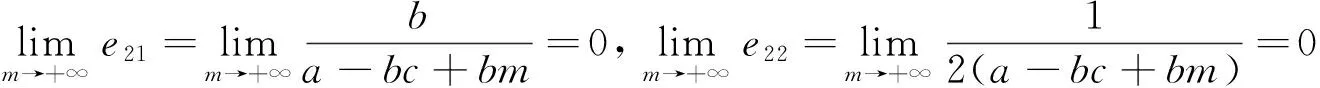
由性质8可知，随着政府补贴定额m的增加，e21和e22的变化趋势分别如图5和图6所示。

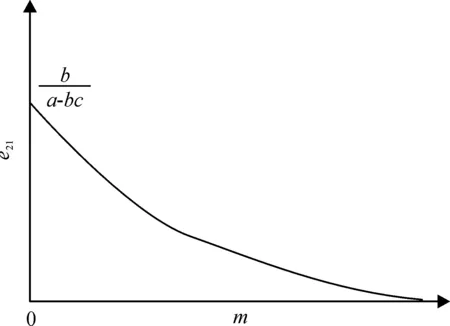
图5　补贴资金使用效率e21与补贴定额m关系

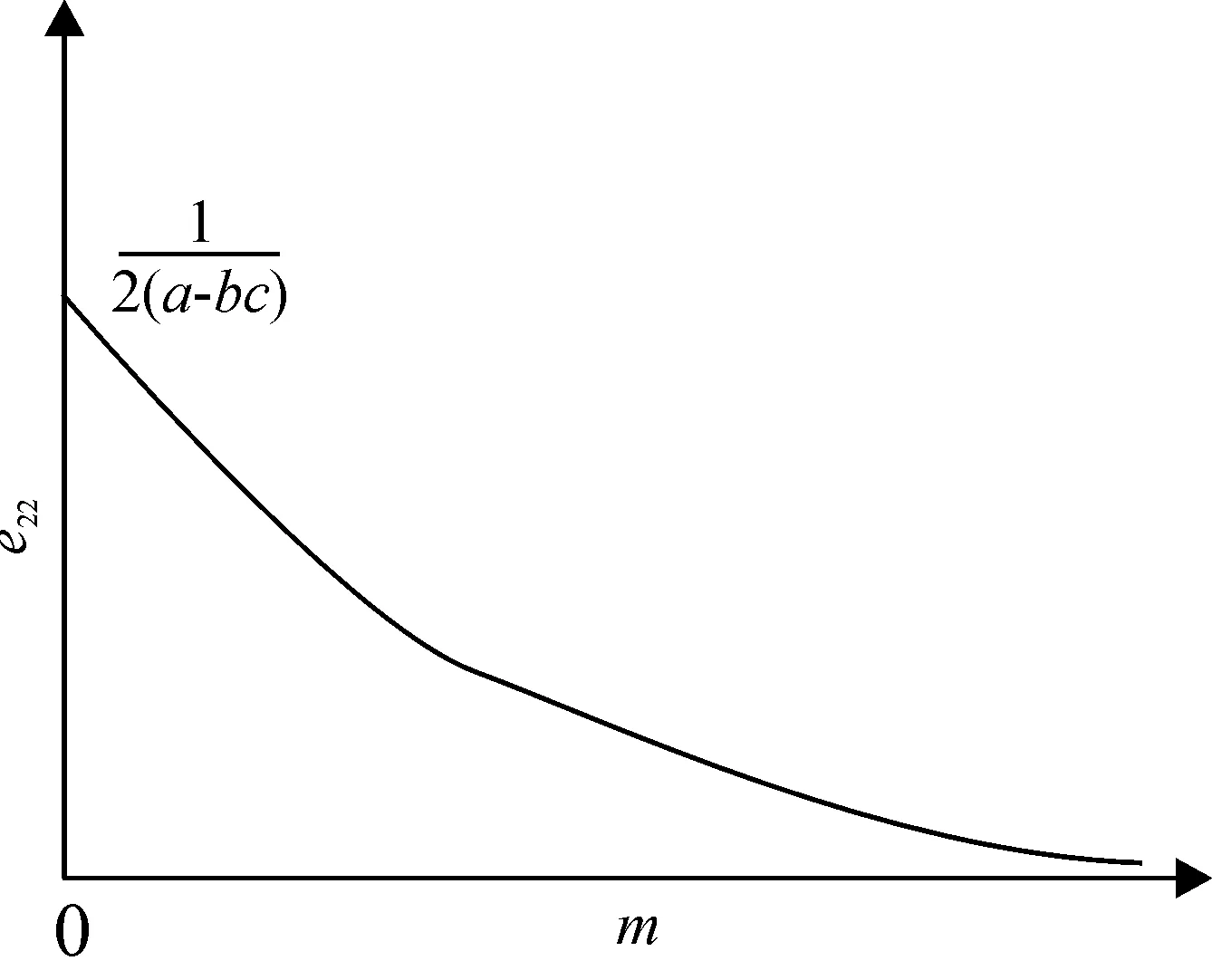
图6　补贴资金使用效率e22与补贴定额m关系

结论4无论是定比补贴还是定额补贴，随着政府补贴力度的增大(η或m的增大)，补贴资金的使用效率均在下降，即单位补贴资金带来的设备应用增加量和单台(套)设备平均剩余增加量均在下降。

3.3补贴资金使用效率比较

在相同的补贴效果下，两种补贴方法所需的补贴资金总额多少可以用来判断两种方法的效率的高低。与政府补贴目标保持一致，补贴效果指“设备应用增加量”和“单台(套)设备平均剩余增加量”。

性质9当两种补贴的补贴效果相同，即Δq1=Δq2和Δs1=Δs2时，有m=cη并且定比补贴的补贴总额M1与定额补贴的补贴总额M2的大小关系为M1>M2。

证明结合式(28)和式(33)并由Δq1=Δq2可得bcη/2=bm/2; 结合式(29)和式(34)并由Δs1=Δs2可得cη/4=m/4。因此：m=cη是两种补贴达到相同补贴效果的充要条件。

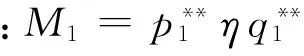
性质9表明，在相同的补贴效果下，定比补贴所需补贴资金额大于定额补贴。换言之，在Δq1=Δq2和Δs1=Δs2同时成立的情况下有e21>e11和e22>e12成立。其中e21>e11表明在以“设备应用增加量”指标来衡量两种补贴方式的资金使用效率时，定额补贴高于定比补贴；而e22>e12表明在以“单台(套)设备平均剩余增加量”指标来衡量两种补贴方式的资金使用效率时，定额补贴依然要高于定比补贴。

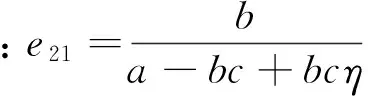
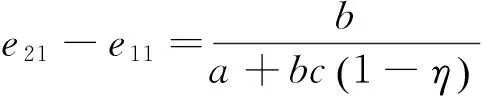
(39)

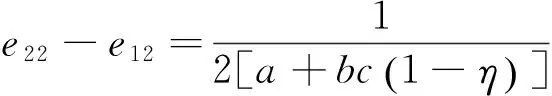
(40)

性质10在两种补贴达到相同的补贴效果即m=cη时，有e21-e11>0和e22-e12>0，d(e21-e11)/dη>0和d(e22-e12)/dη>0以及d2(e21-e11)/dη2>0和d2(e21-e11)/dη2>0。

证明由0<η<1结合式(39)和式(40)可得e21-e11>0以及e22-e12>0。与性质9一致。

又因为

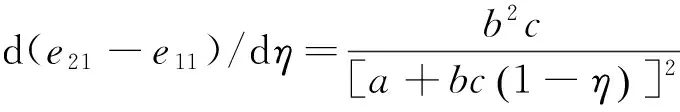
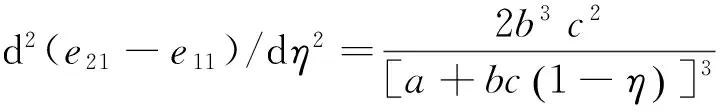
所以由0<η<1可得d(e21-e11)/dη>0且d2(e21-e11)/dη2>0。

同理可知：

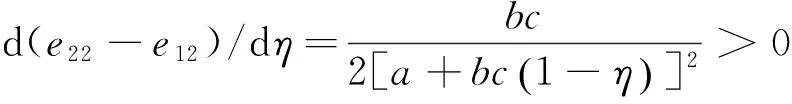
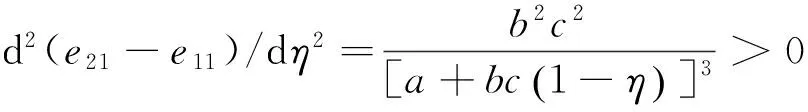
由性质10可知，e21-e11以及e22-e12取值随政府补贴比例η的变化趋势分别如图7和图8所示。

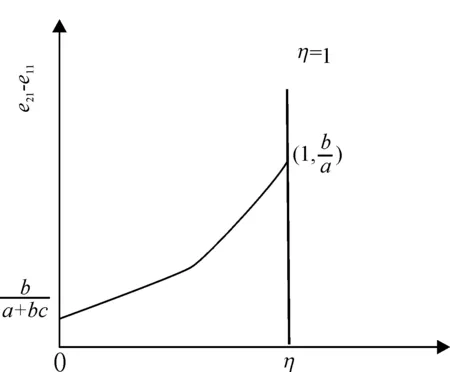
图7　指标1下两种补贴资金使用效率之差与补贴比例的关系

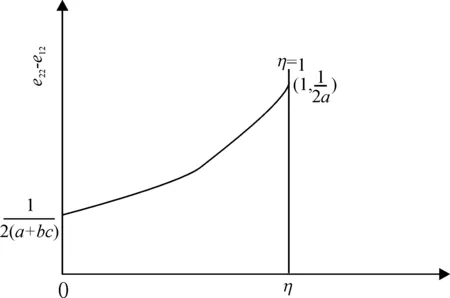
图8　指标2下两种补贴资金使用效率之差与补贴比例的关系

性质10表明，无论补贴力度η(0<η<1)如何变化，只要两种补贴取得相同的补贴效果时即m=cη时，定额补贴的资金使用效率就大于定比补贴。综合性质9和性质10可得结论5。

结论5定额补贴的资金使用效率高于定比补贴；并且随着政府补贴力度的增大，定额补贴与定比补贴的资金使用效率之差在增大,即定额补贴相比于定比补贴在补贴资金使用效率方面的优势随着补贴力度的增大愈加明显。

3.4数值分析

为清楚地表现定比补贴和定额补贴的差异，现赋予参数以具体数值：a=1 000，b=30，c=25。因为定比补贴是按照价格比例η进行补贴而定额补贴是按照定额m补贴的，所以要实现对两种补贴的比较需要统一两者。

在前文已证明：在两种方法到达相同的补贴效果时有m=cη，η∈(0,1)；因此，下文就在相同的补贴效果下考察两种补贴各自所需补贴资金及补贴效果(见表1)、补贴资金使用效率以及它们的差值(见表2)。

表1中“补贴效果”一列表示在m=cη下，两种方法所共同达到的补贴效果(设备应用增加量和平均剩余增加量)；“所需资金”一列表示在达到相同的补贴效果时两种补贴各自需要的补贴资金总额以及差额(定比减定额)。表2中“效率指标1”一列表示用于衡量资金使用效率的“设备应用增加量”指标取值以及两种补贴的差值(定额减定比)；“效率指标2”一列表示用于衡量资金使用效率的“单台(套)设备平均剩余增加量”指标取值以及两种补贴的差值(定额减定比)。

由表1 “所需资金”一列可观察到：在相同补贴效果下，定额补贴所用资金小于定比补贴，并且随着补贴比例增大愈加明显。由表2“效率指标1”和“效率指标2”可知：1)随着补贴比例增大，两种补贴方式的两种资金使用效率指标都在降低；2)定额补贴的资金使用效率高于定比补贴，并且随着补贴比例增大愈加明显。

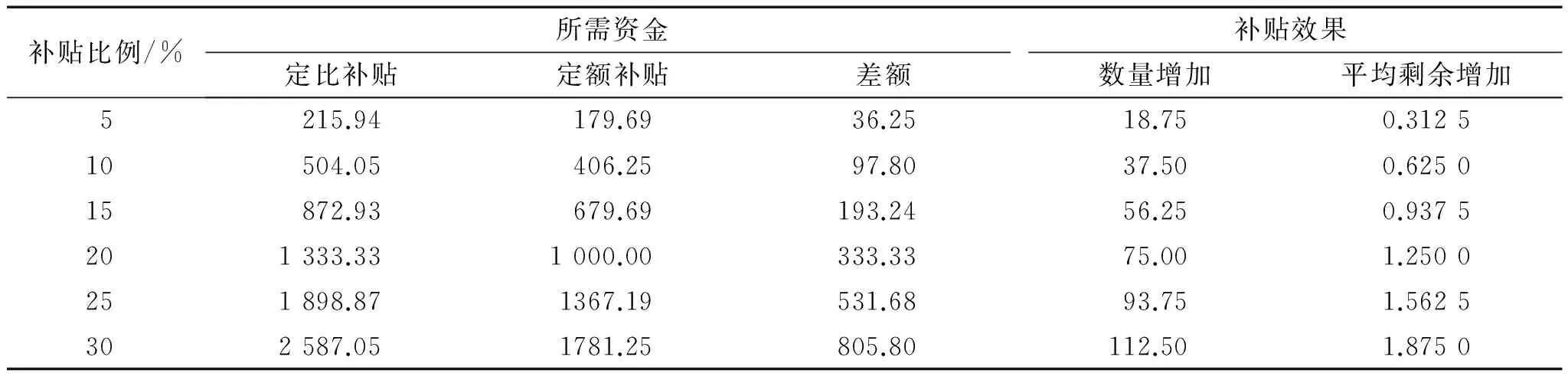
表1　定比与定额补贴效果及所需资金比较

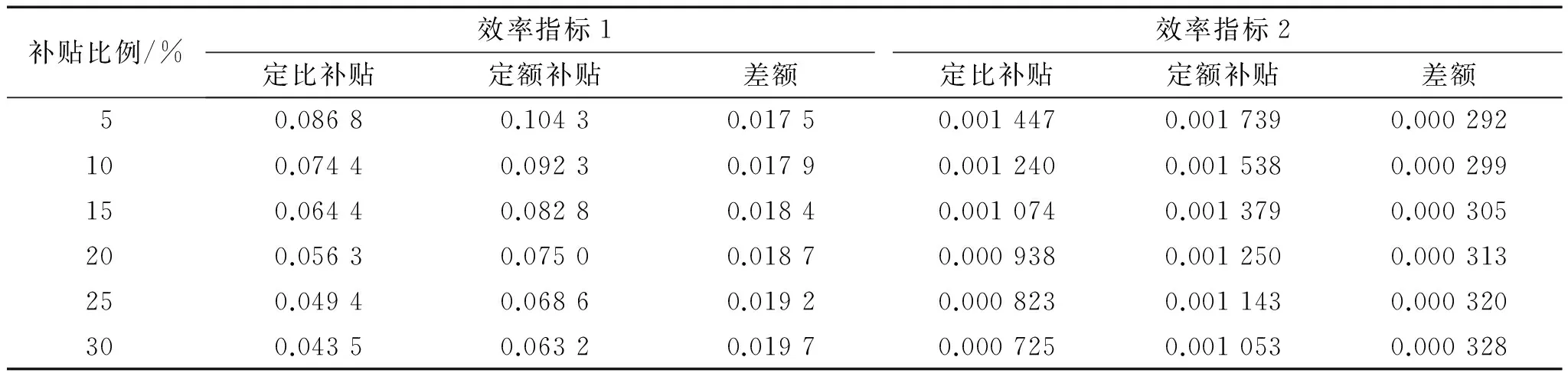
表2　定比与定额补贴效率比较

4　结语

本文先后在定比和定额补贴下建立了“政府-设备供应商-设备应用企业”序贯博弈模型，分别得出了在两种补贴方式下补贴资金在设备供应商和应用企业之间的最优分配；然后在补贴资金最优分配方案下计算并比较了两种补贴方式的资金使用效率。研究表明：1)定比补贴下政府补贴资金在设备供应商和应用企业之间的最佳分配方案是将补贴全部分配给应用企业，而在定额补贴下政府可以将补贴以任意比例在设备供应商和应用企业之间分配；2)两种补贴的效率均随着补贴力度的增大而降低，但是定额补贴的资金使用效率高于定比补贴，并且随着补贴力度的增大，两种补贴效率之差愈大；3)在定比补贴下设备价格会升高，而在定额补贴下设备价格因补贴资金在设备供应商和应用企业之间分配的不同，会出现升高、不变和下降3种情况。

定比补贴和定额补贴各有优缺点和适用范围。因此，政府部门在补贴实施中应针对不同的情况采用不同补贴方式。

1)对于通用性低的设备，政府宜采用定比补贴方式；而对于通用性高的设备，政府宜采用定额补贴方式。定额补贴需要对设备进行分类，分别确定每种类型设备的补贴额度，从而加大了政策制定工作量；但是定额补贴的资金使用效率却高于定比补贴。通用性高的设备应用量大且种类相对不多，而通用性低的设备应用量小且种类多，因此按照设备通用性对设备进行分类，分别应用上述补贴方式可以很好地利用两种补贴方式的优点。

2)在要求补贴的实施不干扰设备市场价格时，政府应采用定额补贴方式并且将对每台(套)设备的补贴定额平均分配给设备供应企业和应用企业。在保证最大化补贴目标时，定比补贴总是使得设备价格升高，而定额补贴却可以使得设备价格保持不变、升高或降低。

3)在只能选择设备供应企业为补贴对象的情况下，政府宜采用定额补贴方式。在保证最大化补贴目标时，定比补贴只允许将补贴全部分配给应用企业，而定额补贴允许将补贴以任一比例分配在应用企业和设备供应企业之间分配。

4)无论是采用定比补贴还是定额补贴，从补贴前期至中期再到后期应遵循补贴力度由小到大的原则，即先以较小的补贴力度刺激一部分企业购买设备，然后再逐渐加大补贴力度刺激其他企业购买设备。从对两种补贴方式的考察中可以看到，两种补贴方式下的补贴资金的使用效率均随着补贴力度增大而下降。这是因为有些企业不需补贴的刺激或只需较小的补贴力度刺激就会购买设备实施“机器换人”，所以较大力度的补贴应用于这些企业时就造成了补贴资金效率的降低。因此，按照补贴力度的由小到大原则实施补贴可以提高补贴资金的使用效率。

政府在根据情况选择补贴方式后，若选择定比补贴则需将补贴全部分配给“机器换人”应用企业，才能发挥补贴最大激励作用；若选择定额补贴则可以将补贴定额以任一比例分配给设备供应商和应用企业，而补贴效果不受影响。

[1]MA W M.，ZHAO Z.，KE H. Dual-channel closed-loop supply chain with government consumption-subsidy[J]. European Journal of Operational Research ，2013,226(2)：221-227.

[2] LUO C L.，LENG M M.，HUANG J，et al. Supply chain analysis under a price-discount incentive scheme for electric vehicles[J]. European Journal of Operational Research，2014,235(1)：329-333.

[3]朱庆华，窦一杰. 基于政府补贴分析的绿色供应链管理博弈模型[J]. 管理科学学报，2011，14(6)：86-95.

ZHU Qinghua，DOU Yijie．A game model for green supply chain management based on government subsidies[J]．Journal of Management Science in China，2011，14 ( 6) :86-95．

[4]徐春秋，赵道致，原白云. 政府补贴政策下产品差别定价与供应链协调机制[J].系统工程，2014，32(3)：78-86.

XU Chunqiu，ZHAO Daozhi，YUAN Baiyun.Products differential pricing and supply chain coordination mechanism under the government subsidy policy[J].Systems Engineering，2014，32(3)：78-86.

[5]张艳丽，胡小建，杨海洪.基于政府财政干涉的绿色供应链销售渠道模型[J].工业工程，2015，18(5)：27-33.

ZHANG Yanli，HU Xiaojian，YANG Haihong.Distribution channel models of green supply chain based on government financial intervention[J].Industrial Engineering Journal，2015,18(5)：27-33.

[6]李友东，赵道致，夏良杰. 低碳供应链纵向减排合作下的政府补贴策略[J].运筹与管理，2014，23(4)：1-11.

LI Youdong，ZHAO Daozhi，XIA Liangjie.Governmental subsidy policy for enterprises’cooperative Behavior inemission reduction in low-carbon supply chain[J].Operations Reseach and Management Science，2014，23(4)：1-11.

[7]HUANG Jian，LENG Mingming，LIANG Liping， et al. Promoting electric automobiles: supply chain analysis under a government’s subsidy incentive scheme[J]. IIE Transactions，2013，45(8): 826-844.[8]罗春林. 基于政府补贴的电动汽车供应链策略研究[J]. 管理评论，2014，26(12)：198-205.

LUO Chunlin.Supply chain analysis for electric vehicle under government’s Subsidy[J].Management Review，2014，26(12)：198-205.

[9]熊中楷，黄德斌，熊榆.政府奖励条件下基于再制造的闭环供应链模式[J].工业工程，2011，14(2)：1-5.

XIONG Zhongkai，HUANG Debin，XIONG Yu. On the closed-loop supply chain modes of product remanufacturing with government reimbursement[J].Industrial Engineering Journal，2011，14(2)：1-5.

[10]徐兵，杨金梅. 闭环供应链竞争下政府补贴效率研究[J].管理工程学报，2013，27(4)：178-185.

XU Bing，YANG Jinmei.The efficiency of government subsidy for closed-loop supply chains[J].Journal of Industrial Engineering and Engineering Management，2013，27(4)：178-185.

[11]张汉江，李聪颖，姚琴,等. 闭环供应链上的最优回收激励契约与政府补贴再制造政策的最优化[J]. 系统工程，2014，32(8)：74-79.

ZHANG Hanjiang，LI Congying，YAO Qin，et al. Optimal recycling incentive contract on closed-loop supply chain and optimization of government subsidy policy of remanufacturing[J].Systems Engineering，2014，32(8)：74-79.

[12]赵晓敏，徐阳阳，林英晖. 纳什均衡市场下政府补贴对再制造的影响效应[J]. 工业工程与管理，2015,20(1)：90-94,99.

ZHAO Xiaomin，XU Yangyang，LIN Yinghui. The effects of government subsidies on remanufacturing in the Nash market[J].Industrial Engineering and Management，2015,20(1)：90-94,99.

[13] MITRAA Supriya, WEBSTER Scott.Competition in remanufacturing and the effects of government subsidies[J]. Int. J. Production Economics，2008，111(2)：287-298.

[14]邱国斌.不同政府补贴模式对制造商与零售商决策的影响[J].科学决策，2013(7)：12-24.

QIU Guobin. Influence on decisions of manufacturer and retailer by different modes of government′s subsidy[J].Scientific Decision Making，2013(7)：12-24.

[15]邱国斌. 不同权重下政府补贴对供应链的影响[J]. 技术经济，2013，32(12)：124-129.

QIU Guobin. Impact of government’s subsidy with different weights on supply chain[J].Technology Economics，2013，32(12)：124-129.

Optimizing Financial Subsidy Types and Allocation on “Replacing Man with Machine”

SUN Yuwei1，2,ZHANG Zhicong2

(1.School of Business Administration，South China University of Technology，Guangzhou 510641，China；2.Department of Industrial Engineering，Dongguan University of Technology，Dongguan 523808，China)

Fixed ratio and fixed volume subsidy, which are two financial subsidy types for “replacing man with machine”, are researched on. Fixed ratio subsidy refers to the government subsidy to the equipment supplier or buyer by a certain ratio of equipment price, while fixed volume subsidy means the government subsidy to the equipment supplier or buyer by a certain volume of money. Based on the game theory, optimal allocation and efficiency of government subsidy to “replace man with machine” are respectively researched under fixed ratio and fixed volume subsidy. First, sequential game models among government, equipment supplier and buyer are established under two subsidy types, and then the optimum subsidy allocations are derived. Then subsidy effectiveness and efficiency under optimum subsidy allocations are analyzed and compared. Last, financial subsidy proposals are given according to characteristics of the two subsidy types. Two main results are found. Firstly, allocating total subsidy to the equipment buyer is optimal under fixed ratio subsidy while under fixed volume subsidy, subsidy effectiveness is constant in all allocation schemes. Secondly, the capital usage efficiency of fixed volume subsidy is higher than that of fixed ratio subsidy.

supply chain；replacing man with machine ；subsidy types and allocation decisions； government-enterprise game；capital usage efficiency

2016- 01- 15

国家自然科学基金资助项目(71201026)；广东省自然科学基金资助项目(2015A030313649)；广东省科技计划项目公益研究与能力建设专项资助项目(2015A010103021)；广东省高等学校优秀青年教师培养计划资助项目(Yq2013156)；广东省教育厅2015年重点平台及科研项目特色创新类项目(自然科学类)资助项目(2015KTSCX137)

孙玉卫(1989-)，男，山东省人，硕士研究生，主要研究方向为物流与供应链管理.

张智聪(1980-)，男，广东省人，教授，博士，主要研究方向为生产系统分析、生产控制与调度、智能优化.E-mail：stephen1998@gmail.com

10.3969/j.issn.1007- 7375.2016.04.015

C934

A

1007-7375(2016)04- 0098- 10