立体几何中正方体的载体作用

安徽省合肥北城中学　尹连辉

立体几何中正方体的载体作用

安徽省合肥北城中学尹连辉

正方体是常见的重要空间几何体，正方体的点、线、面都具有很好的对称性。有些图形看似复杂，但运用割补法将其放入正方体模型中，难度就会降低很多。下面举例说明。

一、正方体与直线

例1若空间中四条不同的直线l1、l2、l3、l4满足l1⊥l2、l2⊥l3、l3⊥l4，则下列结论一定正确的是（）。

A.l1⊥l4

B.l1∥l4

C.l1与l4既不垂直也不平行

D.l1与l4的位置关系不确定

试题分析本题考查空间中直线的位置关系，常规思路是利用所学线线关系进行逐步排除。因为空间直线平行根据公理4具有传递性，但垂直不具有传递性，所以判断起来费时费力。通过观察我们可以看出，题目中所给垂直条件较多，而在正方体中能够轻松找出符合题设所列垂直条件的直线，所以可以考虑把本题中的直线放在正方体中观察。

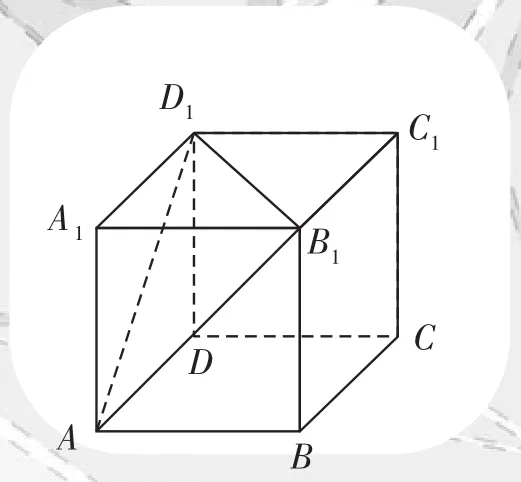
解析如右图所示，在正方体ABCD-A1B1C1D1中，设DD1是直线l1，DC是直线l2，AD是直线l3，若AA1是直线l4，则l1∥l4；若AB是直线l4，则l1⊥l4。故很容易得出l1与l4的位置关系不确定。

二、正方体与三视图

例2一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（）。

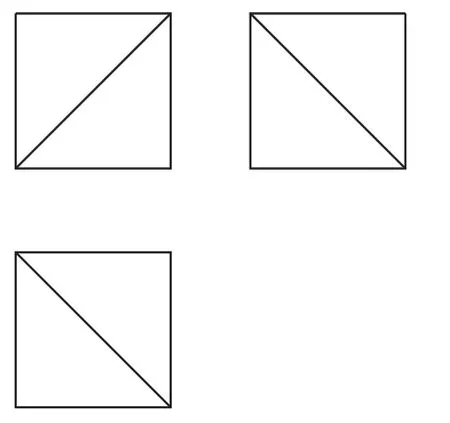
试题分析本题以正方体模型为载体，考查的是识图能力及几何体体积的运算，要求我们能根据三视图还原出几何体，进而求体积比。

三、正方体与命题

例3如右图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A、P、Q的平面截该正方体所得的截面记为S。则下列命题正确的是________（写出所有正确命题的编号）。

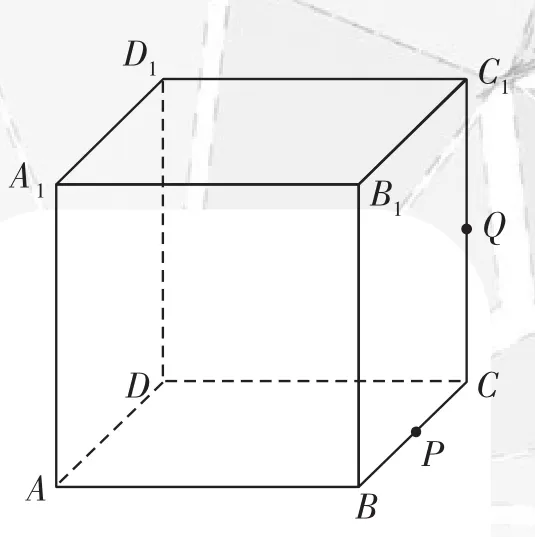
试题分析此类问题除了考查同学们的空间想象能力之外，对思维层次的要求较高，稍不留神就会出错，只有静下心来，沉着冷静地处理该类问题，才能够做好。

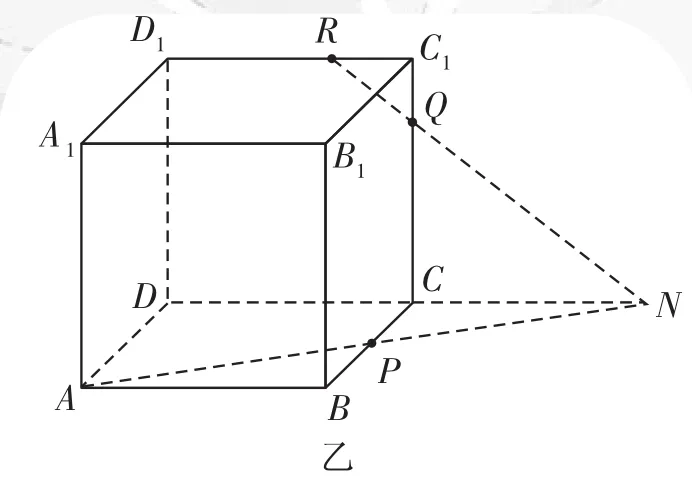
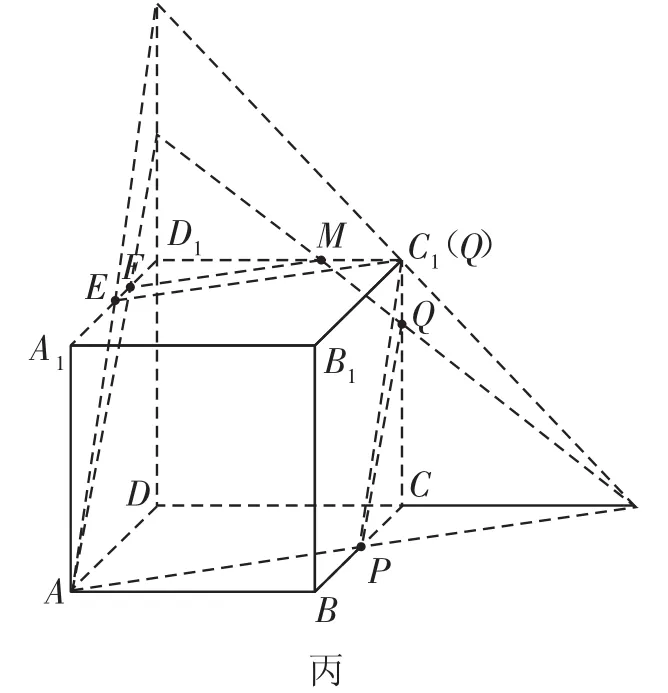
当CQ=1时，截面为APC1E，可知且四边形APC1E为菱形故⑤正确。

四、正方体与排列组合、概率

高考对知识的考查不单单是某个章节的知识点，有时还会和其他知识综合，在知识的交汇处命题，如正方体与排列组合、概率等知识综合考查。

例4从正方体6个面的对角线中任取两条作为一对，其中成的角为60°的共有（）。

A.24对 B.30对 C.48对 D.60对

试题分析本题以正方体为载体，考查排列组合知识，解决问题时应做到不重不漏。

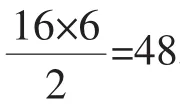
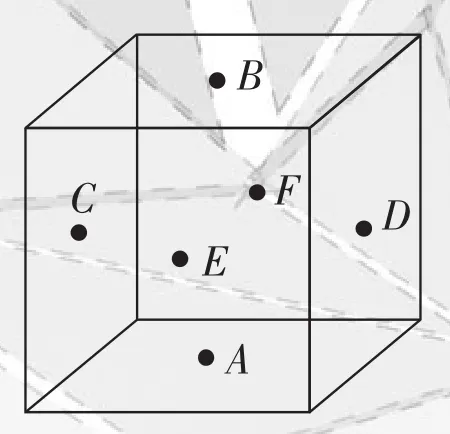
例5考察正方体6个面的中心，甲从这6个点中任意选两个点连成直线，乙也从这6个点中任意选两个点连成直线，则所得的两条直线相互平行但不重合的概率等于（）。

试题分析本题以正方体为载体，考查概率知识，解决问题时应做到不重不漏。

解析如图，甲从这6个点中任意选两个点连成直线，乙也从这6个点中任意选两个点连成直线，共有·=15×15= 225种不同取法，其中所得的两条直线相互平行但不重合有AC∥DB，AD∥CB，AE∥BF，AF∥BE，CE∥FD，CF∥ED，共12对，所以所求概率为，选D。

对模型认识和熟悉的过程实际是巩固基础知识和基本技能的过程。模型就像教材里的常用公式一样，既能直接用来帮助解题，也能作为启发和开拓思路的重要工具，可谓一举多得。因此，我们学习的过程中要注重对像正方体这样的模型的掌握和运用。