油藏开发生产优化近似扰动梯度升级算法

赵　辉,唐乙玮,康志江,张贤松,尚根华

(1.长江大学石油工程学院,湖北武汉 430100; 2.中石化勘探开发研究院,北京 100728;3.中海油研究总院,北京 100027)



油藏开发生产优化近似扰动梯度升级算法

赵辉1,唐乙玮1,康志江2,张贤松3,尚根华2

(1.长江大学石油工程学院,湖北武汉 430100; 2.中石化勘探开发研究院,北京 100728;3.中海油研究总院,北京 100027)

油藏开发生产优化属于高维系统最优控制问题,求解其真实梯度异常困难。给出一种近似扰动梯度的一般式,证明此近似梯度恒为上山方向,且两种常用的无梯度算法SPSA与EnOpt产生的近似梯度分别是该梯度的两种特殊形式;通过引入并优化三角阵进行近似扰动梯度升级,实现其对真实梯度的最优逼近。数值试验结果表明:该升级算法相比标准的SPSA算法优化效率提高了近1倍;在历史拟合基础上使用该算法进行了某实际油藏生产优化,所得注采控制方案降水增油预测效果显著、水驱波及效率明显改善,验证了该算法现场应用的可行性。

油藏; 生产优化; 近似梯度; 无梯度算法; SPSA算法; EnOpt算法

引用格式：赵辉，唐乙玮，康志江，等.油藏开发生产优化近似扰动梯度升级算法[J].中国石油大学学报(自然科学版)，2016,40(2)：99-104.

ZHAO Hui,TANG Yiwei,KANG Zhijiang,et al.Reservoir production optimization using an upgraded perturbation gradient approximation algorithm[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(2):99-104.

油藏开发生产优化[1-5]是近年来油气田开发工程研究的热点问题,作为一种新的油田方案管理决策方法,其核心是借助油藏数值模拟技术在当前油藏地质和生产条件下,通过求解描述油藏生产的最优控制模型,优化油水井的产出和注入控制参数(如井底流压、日注采量等),使油藏的开发处于最佳状态。该问题属于复杂的大系统动态最优控制问题,准确计算目标函数的梯度极其困难,如伴随法[6-7]、有限差分法[5,8]等,基于无梯度算法[4-5,9]求解油藏生产优化已成为当前研究的主要趋势。其中,随机扰动近似梯度(SPSA)算法[10-12]和EnOpt算法[13-14]是优化该问题最常用的两种无梯度算法,它们主要是通过估算优化变量与目标函数的敏感性或相关关系获得近似梯度或概率梯度进行优化,每个迭代步只需若干次目标函数值计算,实现简单、便于应用,但这两种算法所得近似梯度存在一定的伪相关,导致优化效率较低且优化结果随机性强等缺陷。笔者提出一种新的近似扰动梯度升级算法,证明SPSA和EnOpt算法产生的近似梯度是该算法梯度的两种特殊形式,并通过数值试验和实际生产优化算例验证其有效性。

1　油藏生产优化控制模型

油藏生产最优化的思想是:将总生产时间分为若干阶段,通过分阶段调控油水井的生产参数,使各阶段油藏开发的效益总和最大化。把油水井各时间步上的生产参数作为控制变量,采用生产期内的经济净现值(NPV)作为性能指标,建立的油藏生产优化控制模型[2,4,15]为

(1)

s.t.ulow≤u≤uup.

(2)

式中,J为目标函数经济净现值,元;T为总的油藏生产控制时间步;y为油藏状态变量,表征流体的状态分布;ro、rwp和、rwi分别为油的单价、产出废水的处理成本、注水井的注水成本,元/m3;Qo,n、Qwp,n和Qwi,n分别为第n步区块日产油量、日产水量和注水量,m3;e为年利率,%;Δtn为第n步时间步长,d;tn为第n步累积计算时间,d;u、uup和ulow分别为Nu维控制变量及其上下边界。

油藏开发生产优化就是以当前流体的状态y为基础,求取目标函数J的最大值及相应的最优控制u。由于J中不显含u,不能通过解析法获得梯度,而伴随法[6-7]则过于复杂,需要编写伴随阵嵌入数值模拟方程中求解,为此笔者建立一种近似扰动梯度升级算法进行梯度估计，实现该控制模型的求解。

2　近似扰动梯度升级算法

2.1近似扰动梯度的一般式

对于目标函数J,考虑在第l个迭代步的最优控制变量为ul,在其周围进行扰动生成N个控制变量:

ul,i=ul+γΔl,i,i=1,2,…,N.

(3)

式中,ul,i为第l步第i个控制变量实现;Δl,i为扰动向量,服从某一分布;γ为扰动步长。

将N个控制变量带入到油藏模拟中进行运算,利用式(1)可分别求得对应的N个目标函数值J(ul,1),J(ul,2),…,J(ul,N),令ΔJi表示第i个目标函数值与当前最优目标函数值的差值,即

ΔJi=J(ul,i)-J(ul)=J(ul+γΔl,i)-J(ul),

i=1,2,…,N.

(4)

构造近似扰动梯度一般式为

(5)

其中

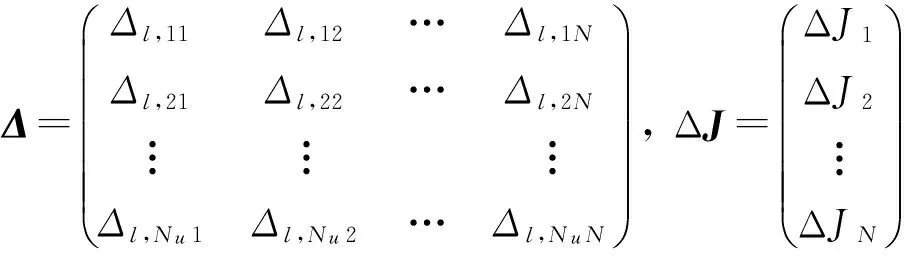
式中,c为常数;L为N维下三角阵。

设g为目标函数在ul处的真实梯度,将J(ul+γΔl,i)在ul处进行一阶泰勒展开,

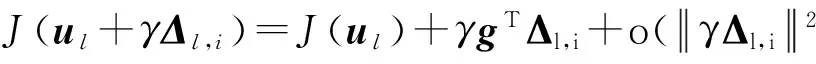
(6)

由于扰动步长γ一般较小,可忽略掉第3项无穷小量,则ΔJi满足,

ΔJi=J(ul+γΔl,i)-J(ul)=γgTΔl,i.

(7)

(8)

对于标准的SPSA算法[10-12],第l步迭代、第i次扰动对应的梯度为

(9)

实际运用中,为获得更好的搜索方向,通常取N次扰动的平均梯度:

(10)

(11)

其中

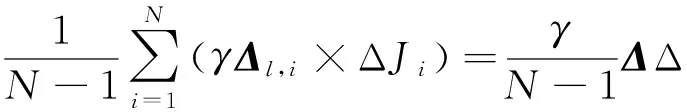
2.2近似扰动梯度升级

近似扰动梯度和真实梯度夹角的余弦值为

(12)

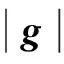
(13)

由于式(13)中除L外都为确定量,不涉及油藏模拟器运算,可以使用传统的优化算法[15]对其进行优化迭代,如最速下降法、拟牛顿法等,其每个迭代步的初值选取可借鉴SPSA算法选取单位阵IN。每个迭代步都对L进行优化,然后采用优化后的L构造梯度,这样得到的梯度更加接近于真实梯度,进而达到改进算法、提高收敛效率的目的。获得近似扰动梯度之后更新控制变量,

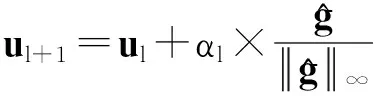
(14)

式中,αl为迭代步长。

2.3算法步骤

运用近似扰动梯度升级算法进行求解时,主要包括外循环和内循环两个过程,外循环是用近似梯度更新控制变量优化目标函数的过程;内循环是通过最大化F求解L得到近似梯度的过程。这里给出近似扰动梯度升级算法的步骤:

(1) 设定初始控制变量u0,并模拟计算出u0对应的初始目标函数值J(u0),确定初始参数取值N和γ,c=N×γ,L=IN,内外循环最大迭代次数lmax和kmax,外循环迭代步l=0。

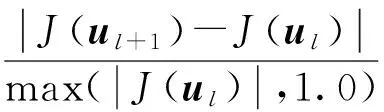
虽然内循环增加了运算量,但它不涉及油藏模拟器的运算,使用传统的优化方法便可对梯度进行快速优化改进。引入L并对其进行优化,使升级算法得到的梯度能够更好逼近真实梯度。

3　实例应用

应用所提出的近似扰动梯度升级算法,首先进行数值试验,对一数学函数进行优化求解并将优化结果与标准SPSA算法结果对比,然后对实际油藏进行生产优化并将优化结果与常规方案结果进行对比。

3.1函数算例测试

目标函数值迭代过程如图1所示,迭代结束时,两种算法都使目标函数收敛到了最优值J=0附近。可以看出,在相同扰动次数下,升级算法的收敛速度远大于标准SPSA算法,升级算法扰动5次取得了标准SPSA算法扰动10次的效果,其优化效率提高了1倍,说明升级算法取得了更好的优化效果。

此目标函数真实梯度容易求得,图2为迭代过程中两算法近似梯度与真实梯度夹角的余弦值。可以看出,在迭代前半段,近似扰动升级梯度较标准的SPSA梯度更接近于真实梯度,而且其中若干点的余弦值等于1或极其接近于1,表明此迭代步梯度几乎与真实梯度相吻合,余弦值的平均值约为0.9,而标准SPSA梯度的夹角余弦值约为0.7,说明升级梯度对真实梯度的逼近效果更好;在迭代接近最优解时,两种算法均产生波动。

图1　目标函数迭代过程Fig.1　Iterative process of objective function

图2　两种算法的梯度与真实梯度的夹角余弦值Fig.2　Cosine of angle between gradient of two algorithms and real value

3.2实际油藏生产优化

选取某油藏单元进行油藏生产优化计算,该单元为含有微裂缝的低渗透油藏,地下情况复杂,水驱开发效果评价显示其注水效率低下,注不进采不出和水淹水窜现象共存,深化注水挖潜和注采结构优化成为当前该油藏提高采收率的重要方向。该单元含油面积2 km2,地质储量70.0×104t,油藏中部深度2 860 m,油层平均厚度4.7 m,地层原油黏度7.8 mPa·s,原始地层压力25.9 MPa,油层平均渗透率7.9×10-3μm2,平均有效孔隙度14%。区块内共24口井,含油井15口和水井9口,累积产油量10.76×104t,累积产水量10.06×104m3,综合含水率72.7%。所建油藏模型采用角点网格系统,共划分了59×65×1=3 835个网格,x方向步长为30 m,y方向步长为40 m。在进行优化之前,基于Eclipse模拟器对该单元进行历史拟合,图3为累积产油量与含水率的拟合结果,整体拟合效果理想,更新后的油藏数值模型能较好地反映地下的实际情况,为后期生产优化提供模型保障。

图3　全区累产油与含水率拟合结果Fig.3　Matching results field cumulative oil production and water cut

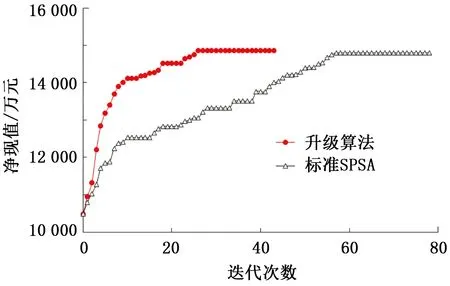
图4　净现值优化结果Fig.4　Optimized results of net present value

基于拟合后的模型进行生产优化,优化前方案采用最后一个时刻工作制度下进行生产,总优化时间为5 a,每个季度约91 d为一个时间步,总共20个时间步,设置原油价格为2 200元/m3,产水成本价格为230元/m3,年利率为10%。图4为梯度升级算法和标准SPSA算法的净现值迭代优化结果。每迭代步进行5次扰动计算,两种算法分别经过42步和79步迭代计算收敛并取得近似净现值优化结果,升级算法的收敛速度提高了约90%,优化后净现值相比优化前均提高了近40%。基于升级算法优化后所得的生产调控方案如图5所示。

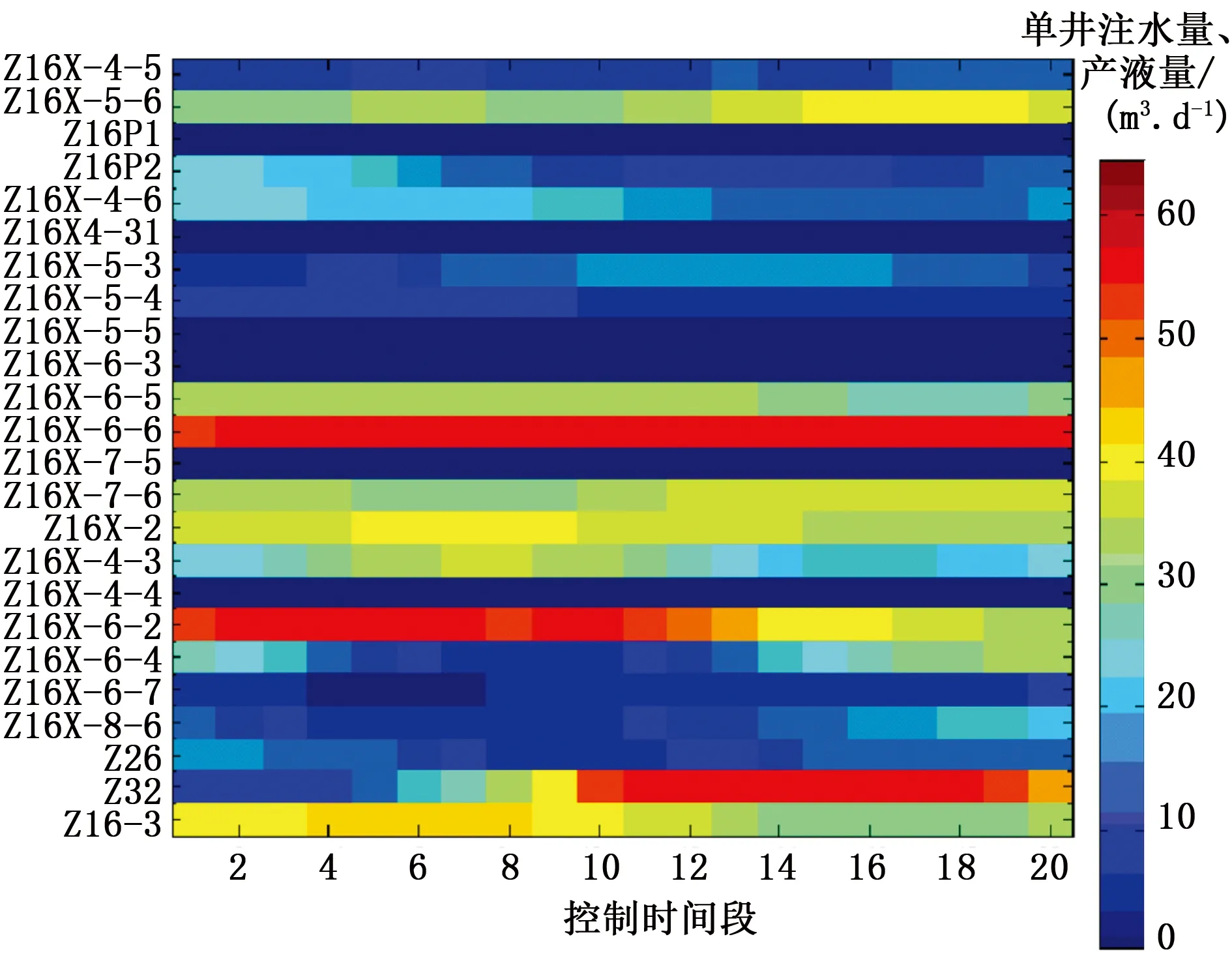
图5　单井注采优化调控结果Fig.5　Optimized well control results

图5中横坐标为控制时间步序列,纵坐标所示为油水井,颜色反映注采参数的变化,生产井对应为日产液量,注水井对应为日注水量,m3。根据所得优化方案,对优化前后区块动态指标和油藏剩余油分布进行了对比分析,结果如图6和图7所示。可以看出,通过对不同时间段内生产制度的调控,优化后区块降水增油明显,波及系数得到了明显的改善,油藏中的剩余油被很好地驱替出来,相比原方案最终含水率下降9.7%、日产油速度平均增加约18 m3,优化期内全区增加产油量3.2×104m3,验证了本文算法进行油藏生产优化控制应用的可行性。

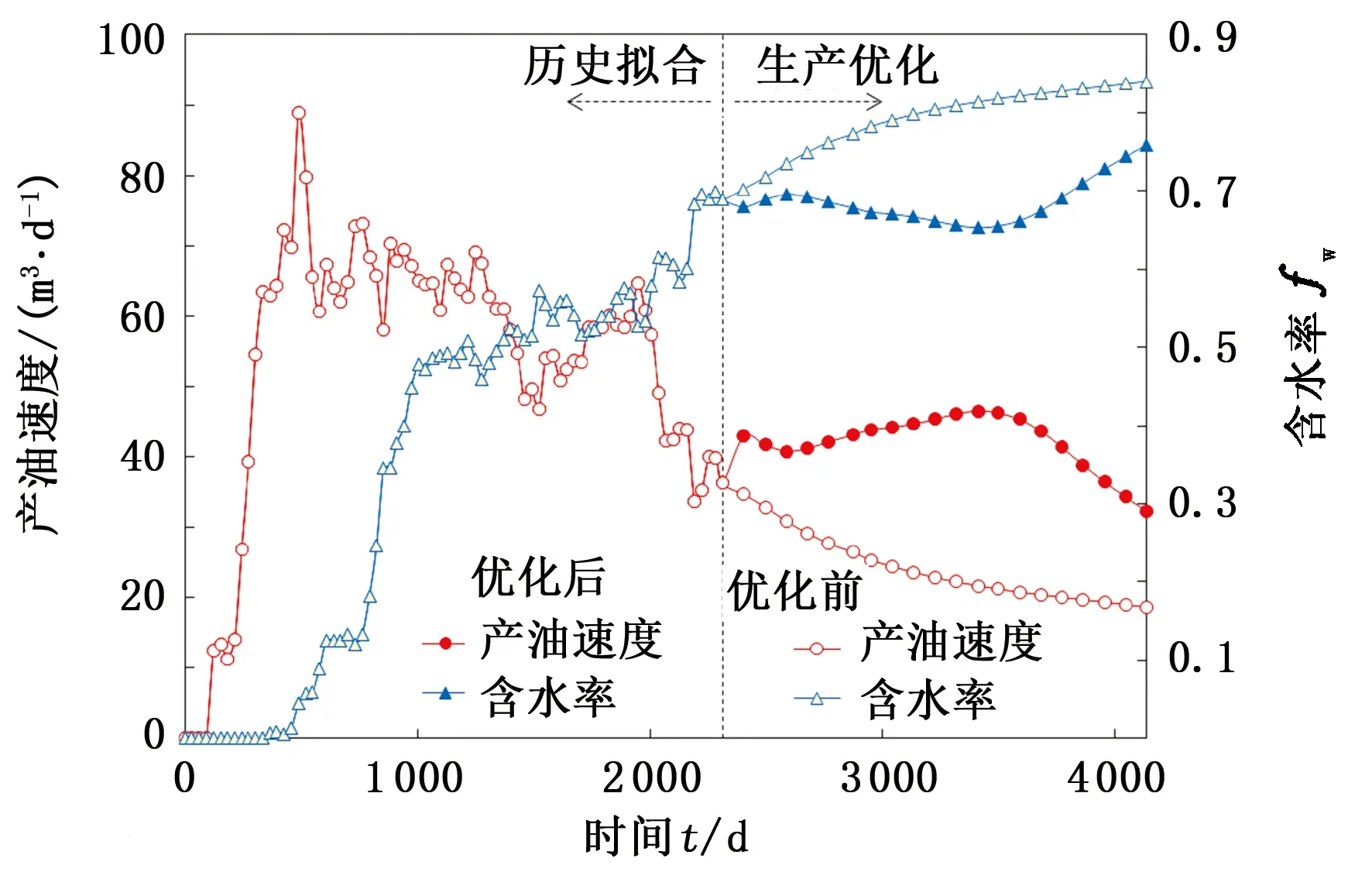
图6　优化全区产油速度与含水率结果Fig.6　Optimized field oil production rate and water cut

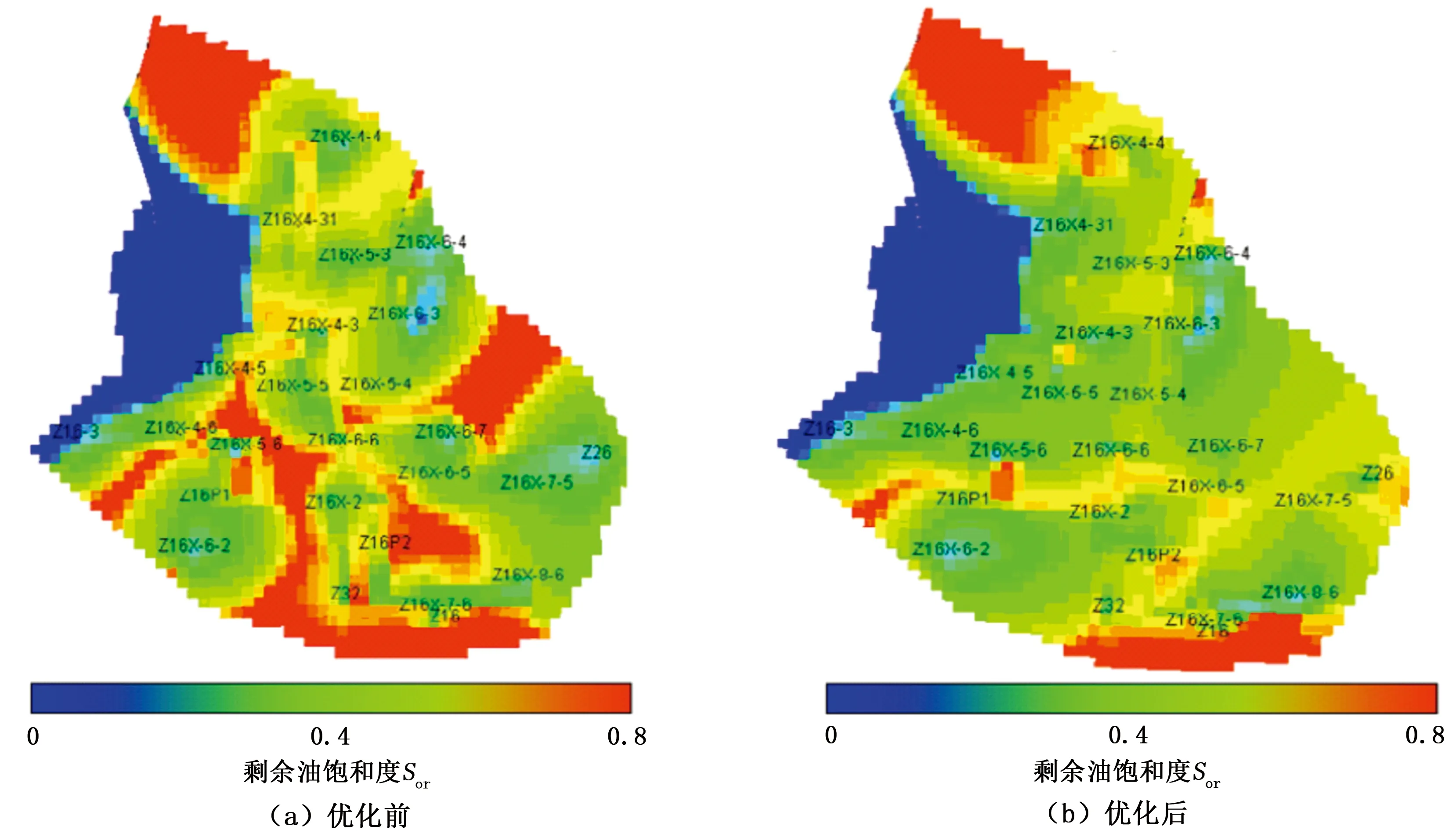
图7　优化前后剩余油分布Fig.7　Remaining oil distribution before and after optimization

4　结　论

(1)提出的近似扰动类算法的梯度一般式的搜索方向具有上山性,且能够将SPSA和EnOpt算法得到的近似梯度统一起来,为今后油藏开发近似梯度算法的研究提供新的角度。

(2)基于一般式梯度提出的近似扰动梯度升级算法这一新优化方法通过引入矩阵L并对其梯度夹角余弦值进行最大化优化,再利用控制变量与目标函数的相关关系得出近似梯度,该梯度能够最佳逼近于真实梯度,利用此算法能够提高优化效率。

(3)函数测试验证显示,升级算法相对于标准的SPSA算法,能使目标函数收敛更加迅速,优化效率提高了近1倍;实际油藏优化结果显示,优化后的方案起到了降水增油的作用,明显提高了开发效益,验证了近似扰动梯度升级算法在油田现场应用的可行性。

[1]BROUWER D,NAEVDAL G,JANSEN J,et al.Improved reservoir management through optimal control and continuous model updating [R].SPE 90149-MS,2004.

[2]ZHAO Hui,LI Yang,YAO Jun,et al.Theoretical research on reservoir closed-loop production management[J].Sci China Tech Sci,2011,54(10):2815-2824.

[3]张凯,李阳,姚军,等.油藏生产优化理论研究[J].石油学报,2010,31(1):78-83.

ZHANG Kai,LI Yang,YAO Jun,et al.Theoretical research on production optimization of oil reservoirs[J].Acta Petrolei Sinica,2010,31(1):78-83.

[4]赵辉,李阳,康志江.油藏开发生产鲁棒优化方法[J].石油学报,2013,34(5):947-953.

ZHAO Hui,LI Yang,KANG Zhijiang.Robust optimization in oil reservoir production[J].Acta Petrolei Sinica,2013,34(5):947-953.

[5]姚军,魏绍蕾,张凯,等.考虑约束条件的油藏生产优化[J].中国石油大学学报(自然科学版),2012,36(2):125-129.

YAO Jun,WEI Shaolei,ZHANG Kai,et,al.Constrained reservoir production optimization[J].Journal of China University of Petroleum (Edition of Natural Science),2012,36(2):125-129.

[6]SARMA P,DURLOFSKY L,AZIZ K.Implementation of adjoint solution for optimal control of smart wells[R].SPE 92864,2005.

[7]BROUWER D,JANSEN J.Dynamic optimization of water flooding with smart wells using optimal control theory [J].SPEJ,2004,9(4):391-402.

[8]WANG C,LI G,REYNOLDS A C.Production optimization in the context of closed-loop reservoir management [R].SPE 109805,2007.

[9]CONN A R,VICENTE K S L.Introduction to derivative-free optimization [M].Philadelphia:MPS-SIAM Series on Optimization,SIAM,2009.

[10]SPALL J C.Multivariate stochastic approximation using a simultaneous perturbation gradient approximation [J].IEEE Transactions Automat Control,1992,37(3):332-341.

[11]SPALL J C.Implementation of the simultaneous perturbation algorithm for stochastic optimization [J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(3):817-823.

[12]SPALL J C.Adaptive stochastic approximation by the simultaneous perturbation method [J].IEEE Transactions on Automatic Control,2000,45(10):1839-1853.

[13]CHEN Y,OLIVER D S,ZHANG D.Efficient ensemble-based closed-loop production optimization [J].SPE Journal,2009,14(4):634-645.

[14]CHEN Y,OLIVER D S.Ensemble-based closed-loop optimization applied to brugge field [R].SPE 118926,2009.

[15]袁亚湘,孙文瑜.最优化理论与方法[M].北京:科技出版社,1999.

(编辑李志芬)

Reservoir production optimization using an upgraded perturbation gradient approximation algorithm

ZHAO Hui1,TANG Yiwei1,KANG Zhijiang2,ZHANG Xiansong3,SHANG Genhua2

(1.College of Petroleum Engineering,Yangtze University,Wuhan 430100,China;2.Research Institute of Exploration and Development,SINOPEC,Beijing 100728，China;3.CNOOC Research Institute,Beijing 100027,China)

Reservoir production optimization is a high-dimensional optimal control problem,and it is very difficult to obtain a true gradient.In this paper,a general perturbation gradient approximation method was presented,and the gradient resolved was always in uphill direction.The commonly used SPSA and EnOpt algorithms,being derivative-free,can be considered as special cases of the general perturbation gradient approximation.The perturbation gradient approximation can be upgraded by introducing an optimized lower triangular matrix for approaching to the true gradient.The numerical simulation results show that,compared with the standard SPSA algorithm,the optimization efficiency of the upgraded algorithm can be increased nearly 100%.In a real case study,the reservoir production optimization was conducted using the new method on the basis of history matching.The field data have shown remarkable increase on oil production and decrease of water production,and the sweeping efficiency of water flooding is significantly improved,which validates the feasibility of the algorithm for practical applications.

reservoir; production optimization; approximate gradient; derivative-free algorithm; SPSA algorithm; EnOpt algorithm

2015-04-29

国家科技重大专项(2016ZX05014003)；国家自然科学基金项目(51344003)

赵辉(1984-)，男，副教授，博士，研究方向为油气田开发工程。E-mail:zhaohui-712@163.com。

1673-5005(2016)02-0099-06doi:10.3969/j.issn.1673-5005.2016.02.012

TE 323

A