基于LMBP神经网络的战斗机综合作战效能评估

吴欣蓬，屈高敏

(西安航空学院 飞行器学院，陕西 西安 710077)



基于LMBP神经网络的战斗机综合作战效能评估

吴欣蓬，屈高敏

(西安航空学院 飞行器学院，陕西 西安 710077)

针对双重任务战斗机一机多能、功能复合的发展趋势，在融合空空、空地作战需求的效能评估指标体系基础上，引入LM算法的BP神经网络对该类战斗机的综合作战效能进行了建模、评估。利用人工神经网络良好的函数拟合和预测能力建立指标与效能值之间的非线性关系，并借助网络优良的容错性解决样本数据残缺或存在错误等问题。最后，采用Matlab神经网络工具箱进行建模，对6种机型进行了计算；并将本模型评估值同另外两种模型评估值进行了对比分析，结果表明该模型是合理、可行的。

战斗机；综合作战效能评估；LM算法；BP神经网络

0　引言

随着数字化技术在超音速战斗机上的逐步深入应用，战机的航电系统在空空模式和空地模式之间切换变得十分容易，双重任务战斗机的发展也日趋成熟。如美国将最初研制的对空F-18战斗机和对地A-18攻击机，通过数字化技术融合，研制出能实现“双重任务”的F/A-18。而作为取代F-15的下一代战斗机F-22，其双重任务作战能力远优于前者。俄罗斯从苏-27到苏-30的发展轨迹上亦是走了“双重任务”的路线，而西欧新研制的第四代战斗机全部都是双重任务战斗机[1]。综上所述，超音速战斗机的这种功能复合、一机多能的发展趋势是十分明显的。如何科学合理地评估这种双重任务战斗机的综合作战效能，是航空装备发展论证以及军事运用等领域研究的重要课题。

传统的战斗机综合作战效能评估方法主要是线性的评估方法，如对数法[2]、综合指数法[1]等。对数法存在任务分配系数是静态的，以及其参数重复计算等问题；而综合指数法中的权重系数大多采用主观赋权法，因此容易引入人为失误因素。并且，这些线性方法难以处理指标信息模糊、样本不完整等复杂数据环境下的评估问题，即线性方法的泛化能力和预测能力不佳[3]。

鉴于人工神经网络(ANN)具有在复杂数据环境中捕获线性或非线性趋势的能力，并能在干扰信号环境和输入新数据的情况下提供可靠预测，具有良好的容错性，是一种客观的人工智能方法，因而克服了线性方法的不足[4]。本文基于LM算法，运用BP神经网络建模，对6种机型进行了战斗机综合作战效能评估，比对其他方法的评估结果，验证了其合理性、可行性。

1　指标体系的建立

现代双重任务战斗机的作战是系统与系统之间的整体对抗，因此其指标的选取必须要在尽可能少且易于测算的基础上客观全面地反映战机的主要功能、敏感地反映战机的性能特征，同时指标之间还要保持适当的独立性，才能得到合理的评估指标体系，并最终得出可靠的评估结果。本文结合双重任务战斗机的特点，参考朱宝鎏《作战飞机效能评估》[2]，融合空对空、空对地作战效能指标，建立了3层战斗机综合作战效能评估指标体系，如图1所示。

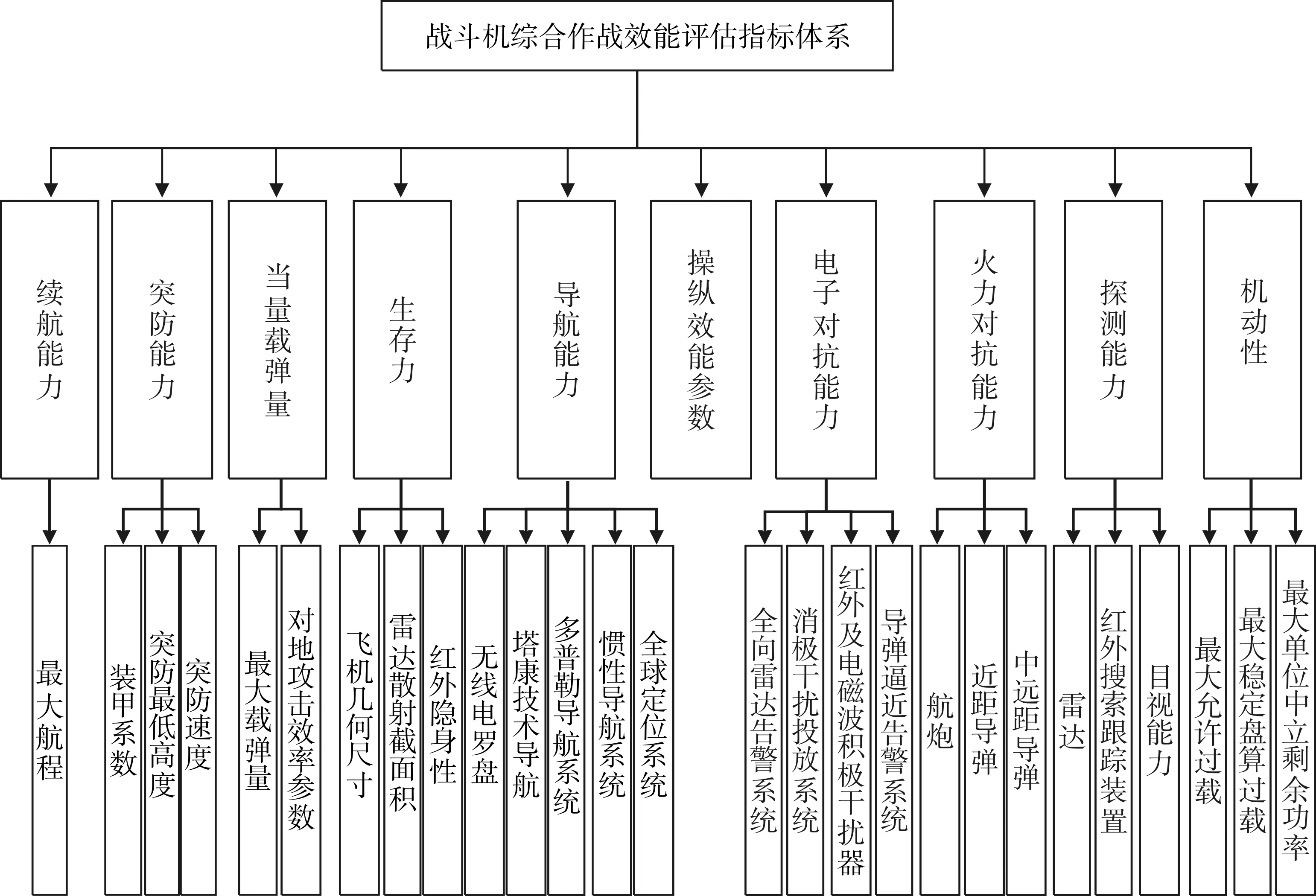
图1战斗机综合作战效能评估指标体系

2　基于LM算法BP神经网络的战斗机综合作战效能评估

运用LM算法BP神经网络对战斗机的综合作战效能进行评估的思路是：将战斗机的综合作战效能评估指标数据作为BP神经网络的输入，而对应的战斗机综合作战效能值则是网络的输出。由于处理的信息量并不是十分大，因此构建3层BP神经网络。然后将预先设置好的理论指标数据和对应的理想综合作战效能评估值作为训练样本，输入到BP神经网络中，使网络采用LM算法进行学习，反复训练至产生一个误差最小的确定网络模型，即拟合得到评估指标数据与综合作战效能值之间的一个合理非线性关系。从而，实现对战斗机综合作战效能的定量评估。

2.1LM算法BP神经网络的建立

本文采用的BP神经网络是多层感知器(MLP)神经网络中的典型代表，其结构为一个输入层I、若干隐含层H和一个输出层O；而层与层之间通过权重系数进行连接。输入网络的数据经过加权后，进行收集，通过激励函数等相关处理，进入下一层，直到产生最后输出；通过与预先设定好的期望输出值比较，从而将误差反向传播，逐步修正网络的相关参数；经过这样不断地训练学习，改变连接神经元之间的权重系数，直至网络的误差MSE最小。

2.1.1指标数据的归一化处理

设有m架待评机型，选取n个评估指标。对于第j个机型的第k个指标xj(k)，其归一化后的表达式为：

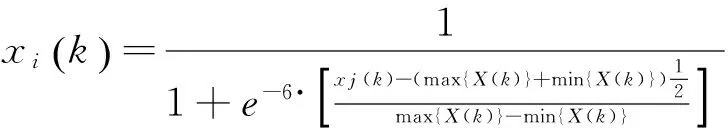
(1)

其中，k=1, 2,…,n；i=1, 2,…,m；j=1, 2, …,m；min{X(k)}：表示同类指标中的最小值；max{X(k)}：表示同类指标中的最大值[1]。

2.1.2训练样本的构造

依据专家对战斗机综合作战效能的评价、各指标因素的上下限等资料，将综合作战效能值对应的指标数据组进行等级划分，获得BP神经网络的训练样本[6]。其中，等级划分要求如下：

(1)若输出结果取值在(0.8,1 )，则综合作战效能级别为优；

(2)若输出结果取值在(0.6,0.8]，则综合作战效能级别为良；

(3)若输出结果取值在(0.4,0.6]，则综合作战效能级别为中；

(4)若输出结果取值在(0.2,0.4]，则综合作战效能级别为差；

(5)若输出结果取值在(0,0.2]，则综合作战效能为级别劣；

(6)若输出结果取值为1(允许数据向下浮动0.05)，则综合作战效能为级别最好。

2.1.3BP神经网络的设置

由于需要处理的数据规模不大，因此本文设置了一个输入层I、一个隐含层H和一个输出层O的3层BP神经网络。而由于选定了10项评估指标，因此输入层由10个神经元构成；按照2.1.2中所述，输出层由6个神经元构成。对于隐含层神经元个数的确定，传统的经验公式法只适合确定一个粗略的数值，并不一定能使人工神经网络的拟合效果达到较好的状态。因此，这里采用“试凑法”对隐含层神经元个数进行确定。当某一隐含层神经元个数能使网络误差最小，即为最佳隐含层神经元个数(可以通过Matlab编程实现)。而对于激励函数，本文采用对数型Sigmoid函数作为BP神经网络的激励函数，即：

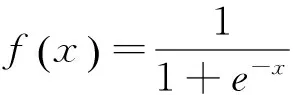
(2)

建立好的BP神经网络如图2所示。

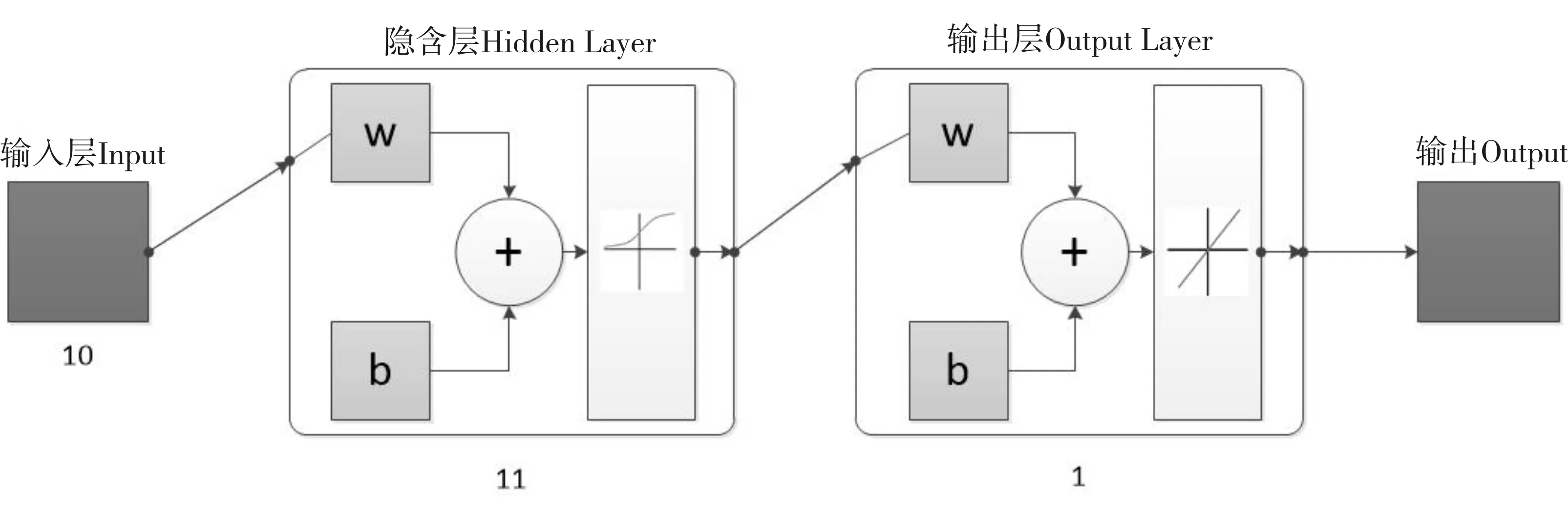
图2BP神经网络示意图

2.1.4学习方法

LM算法，即Levenberg-Marquardt算法。实验发现，LM算法优于梯度下降法、最速下降法以及高斯-牛顿法，其收敛速度较后三者更快[4]。故本文采用LM算法作为网络的学习方法。具体步骤如下[7]：

步骤1初始化权值向量(其分量为一些随机值)；

步骤2按下式更新权值向量：

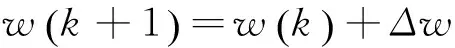
(3)

步骤3求Δw：

设误差权重函数MSE为E(w):

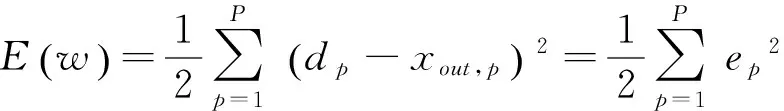
(4)

其中，w表示网络所包含的所有权值向量；dp是期望输出；xout,p是第p组训练数据的实际网络输出。

则E(w)的最小值所对应的最优权重系数集合可通过迭代进行寻找。对第k个神经元，Δw=-Hk-1gk。其中，矩阵H-1∈RN×N是Hessian矩阵H的逆，表示为R=H-1；向量g∈RN×N表示误差权重函数的梯度。

由雅克比矩阵J∈RP×N：

(5)

可知，在点w=w(k)处有：

(6)

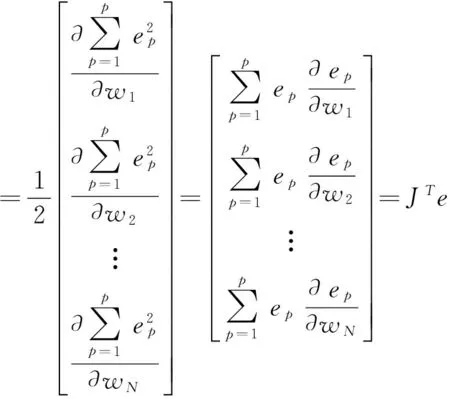
(7)

H≈JTJ

(8)

但这种近似可能导致逆R是奇异矩阵，抑或是病态的，故对Hessian矩阵H进行修改：

H≈JTJ+μI

(9)

其中，系数μ极小，μ=eλ，λ是一个变量。LM算法实质是通过控制λ的变化，使得MSE逐渐减小，这也就决定了LM算法内部到底是向最速下降法靠近，还是向高斯-牛顿法靠近[4]；I∈RN×N，表示一个N×N单位矩阵。

则LM算法的权值更新式为：

(10)

按式(10)反复迭代计算，直至满足误差最小或者达到迭代最高次数，则停止计算。而阈值b的更新类似于此；网络的前向传输与误差反向传播的推导计算过程，详见文献[3][7]。

2.2BP神经网络的训练

本文基于Matlab中的神经网络工具箱，对评估战斗机综合作战效能的LM算法BP神经网络进行了建模。按照上述内容进行了相关参数的设置，并运行软件对网络进行训练。当网络的误差达到最小或者达到最大训练次数时，停止训练，检验相关曲线、数据，确定网络是否合理、满足要求。保存此网络的权重系数和阈值，然后用此训练好的BP神经网络，对战斗机的综合作战效能进行评估。

值得注意的是，BP神经网络模型中最主要的问题是：训练过程中，权值的不断修正改变，网络能否保持原有性能的稳定，即网络对权值扰动是否具有鲁棒性。本文研究发现，由于训练样本有限，因此在Matlab中进行实验时，经常会出现实验结果不能令人满意的情况,出现了过拟合或者拟合不足，即网络对权重扰动的鲁棒性不佳。

不过，通过分析误差曲线、相对误差数据、输出的实际结果是否符合客观实际情况等途径，可以判断该组实验的成功与否，进而通过相关方法修正，再次实验。

Samarasinghe S.等研究表明，采用及早停止等方法可以改进ANN的上述问题，使其保有鲁棒性[4]；而当权重采用随机采样的方式获得时，ANN在用不同随机训练样本寻找最优权值方面具有鲁棒性；一般来讲获得的数据越多，网络的泛化能力越好，过拟合越小，越保有鲁棒性。显然，在Matlab中神经网络的权重数值是随机采样得到的，符合上述内容。而Matlab神经网络工具箱还具有及早停止法的功能，它会将训练数据划分为训练样本(Training set)、验证样本(Validation set)和测试样本(Testing set)三部分。ANN利用Training set计算误差梯度、权值系数和阈值；ANN训练开始时，Validation set的误差开始下降，但是一旦出现过拟合，Validation set的误差会不降反升；在Matlab中通过设置Validation set误差反向的次数，则达到该次数，ANN就会停止训练并记录权值系数和阈值。Testing set主要用于比较不同模型的仿真效果，不用于训练过程。

上述两方面提高了ANN对权值扰动的鲁棒性，最终可以训练得到比较合适的模型。

3　计算与分析

为了检验该基于LM算法BP神经网络的战斗机综合作战效能评估模型的合理性、可行性，本文利用Matlab神经网络工具箱进行了建模与仿真计算。

3.1训练样本与评估样本

依据朱宝鎏《作战飞机效能评估》[2]，选取了6个机型进行战斗机综合作战效能评估，按照2.1中所述得到训练样本和评估样本。其中，训练样本如表1所示；待评估机型的指标数据如表2所示，对应Sigmoid函数归一化处理结果如表3所示。

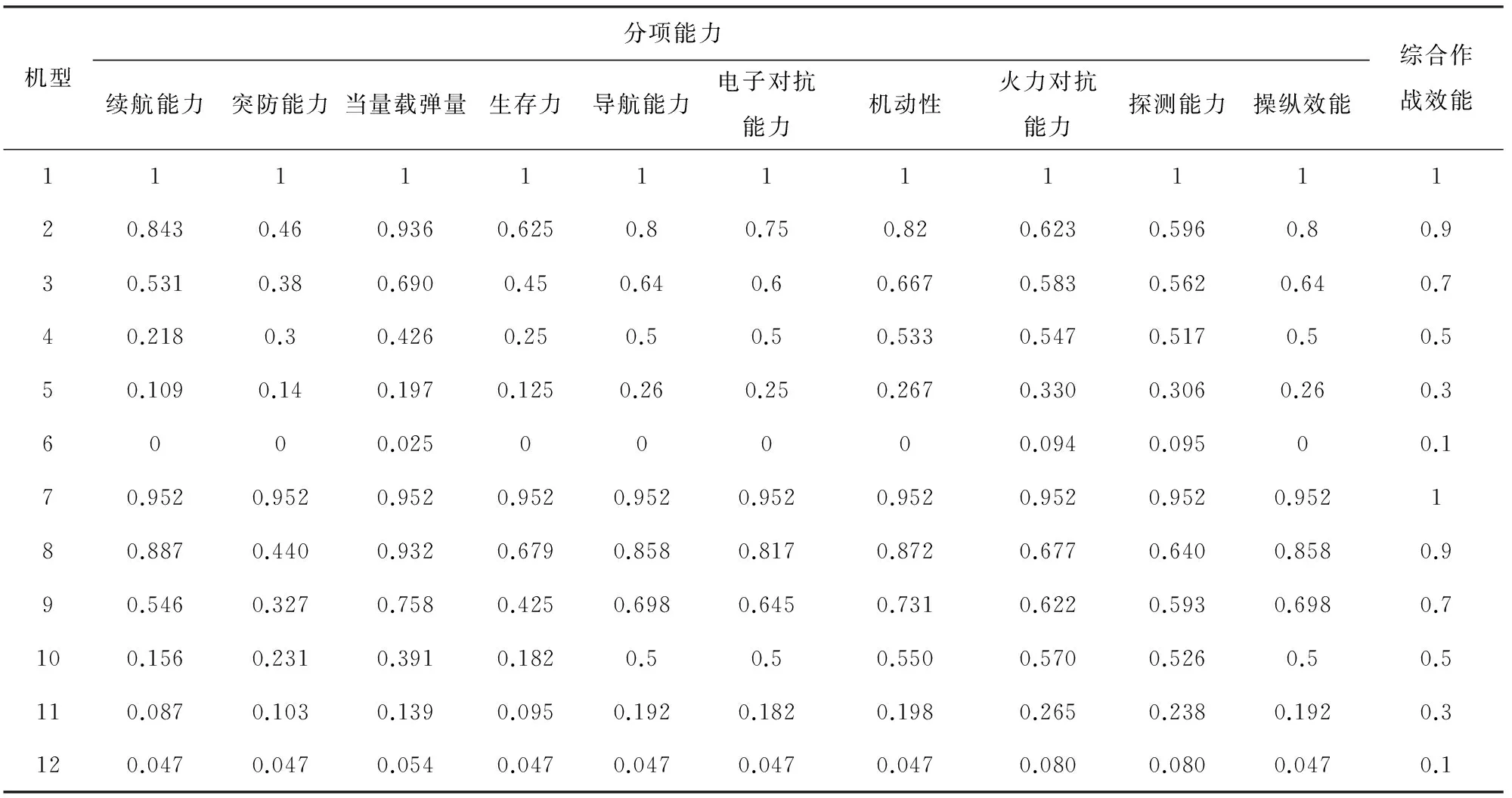
表1　训练样本

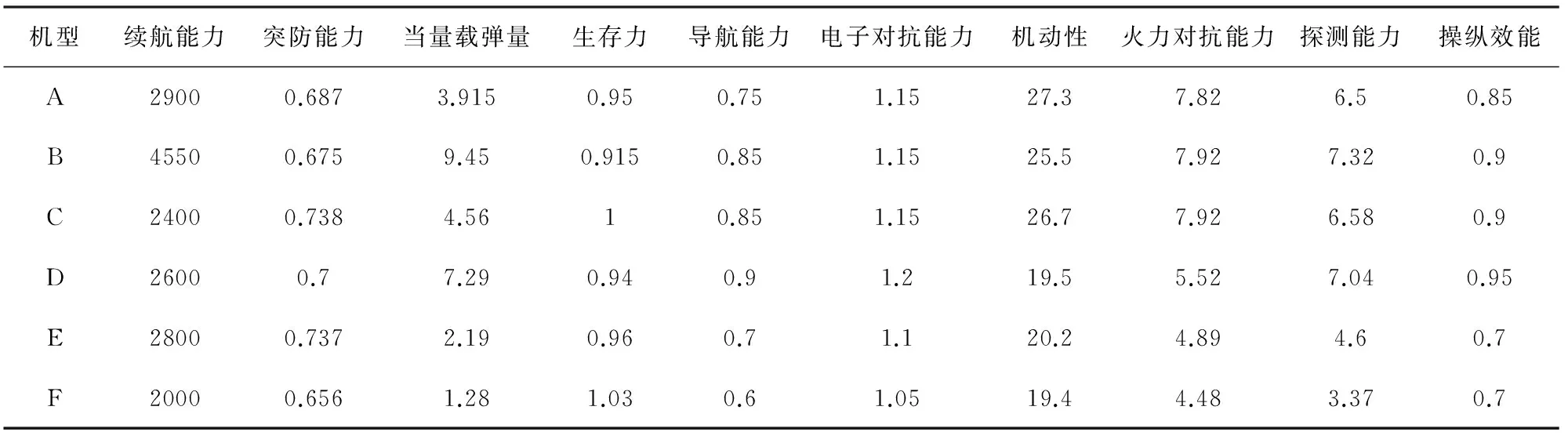
表2　指标数据

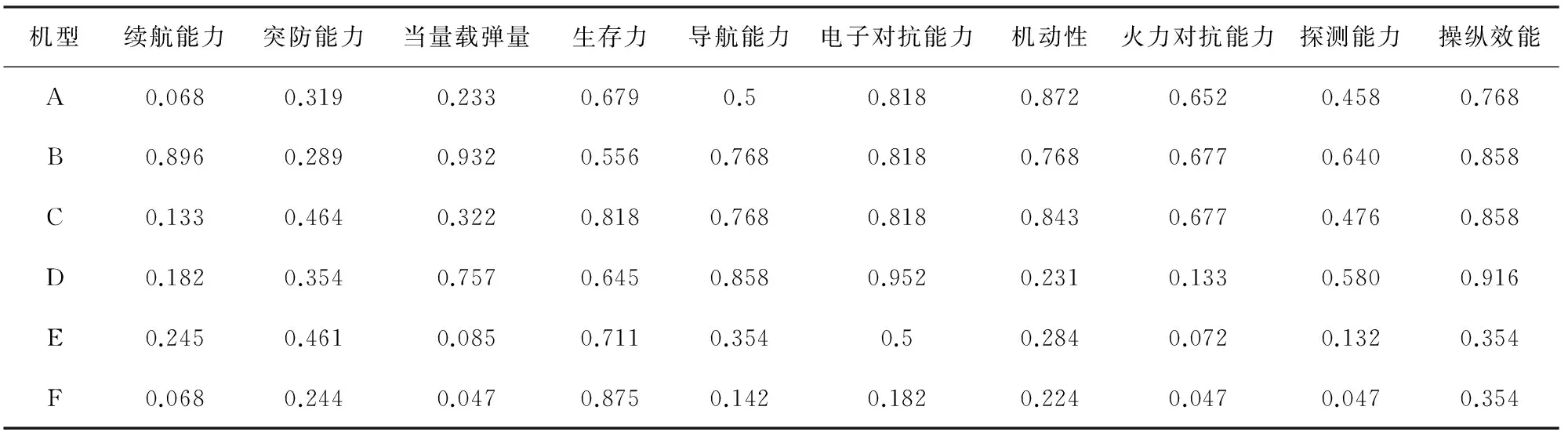
表3　归一化处理的指标数据结果

3.2隐含层神经元个数的确定

采用“试凑法”确定隐含层神经元个数，其测试数据如表4所示。只有当隐含层神经元个数为11时，网络输出结果的相对误差有3项达到10-5或更小，有网络误差最小。

表4　隐含层神经元数目与网络性能

3.3BP神经网络的训练

Matlab中的LM算法BP神经网络模型，设定参数μ为0.001，而其变化上下限设置不可过大，否则及早停止法难以产生效果。学习精度设置为1×10-9，最大训练次数设置为1000，最大出错数为6，其他为默认值。该网络模型经过0～44共45次训练就收敛了，充分说明了LM算法的高效性。最终得到网络相关参数曲线，如图3、图4所示。

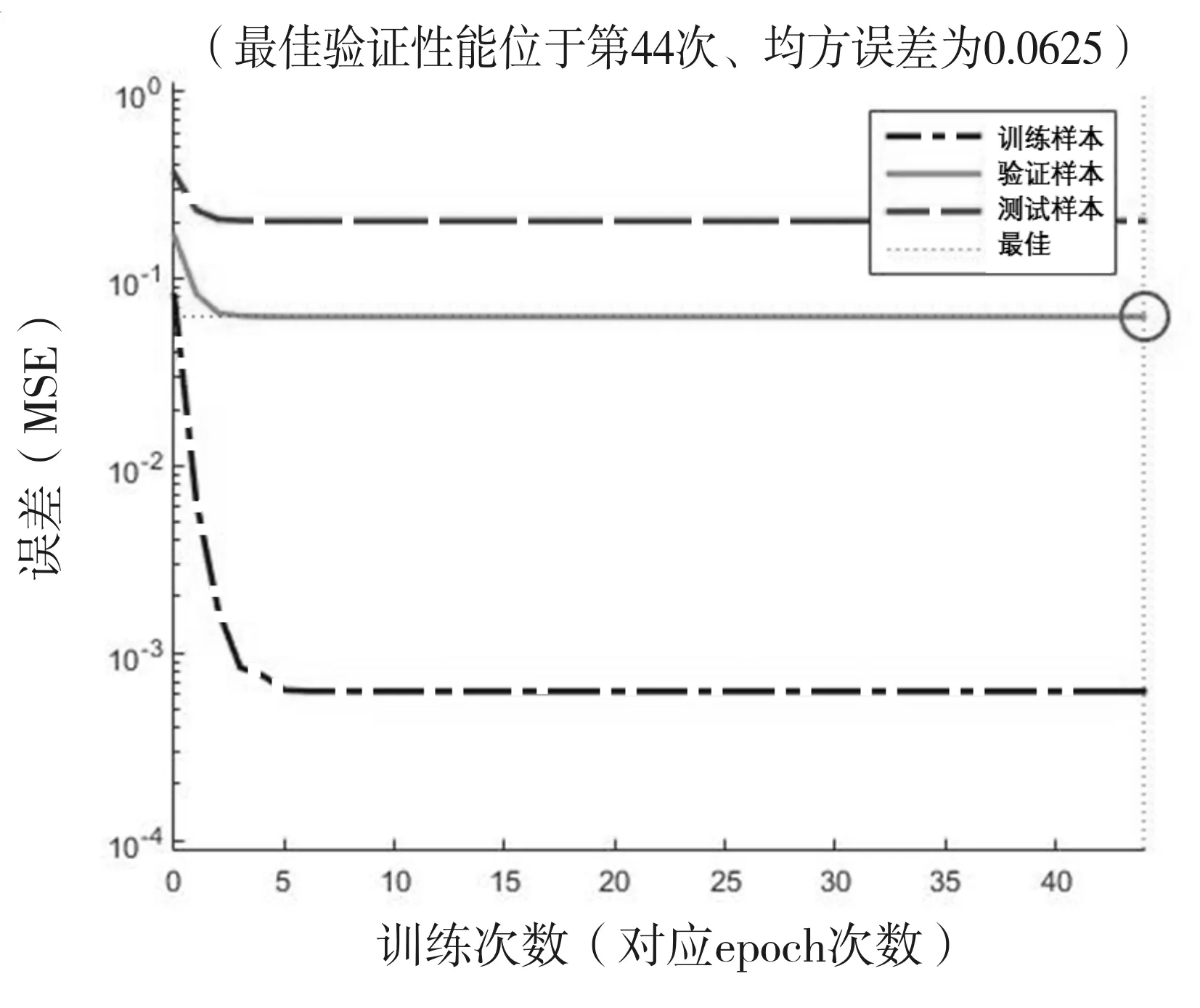
图3　误差变化曲线

由于在Matlab中使用了及早停止法，因此软件会自动按比例将样本划分为三部分，故对应3组曲线如图3所示，均呈现出误差随迭代次数增加而下降的趋势，故BP神经网络整体呈现收敛趋势，至最终收敛。整个曲线基本光滑，中间段没有突然凸起的部分，说明在训练过程中没有出现不收敛的错误状态，这也反映在图4的第三幅图中，即验证样本检测到错误的情况在45次迭代过程中始终为0。因此，该训练得到的BP神经网络模型是可靠的。

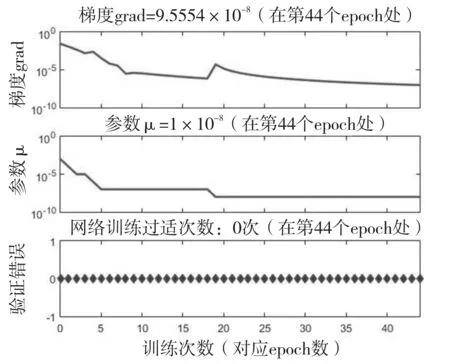
图4　训练状态图

*注：网络训练过适次数，即网络训练时，验证误差大于训练误差的次数。

3.4效能评估计算

采用训练好的LMBP神经网络对6架战斗机进行了综合作战效能评估，其评估结果如表5所示。

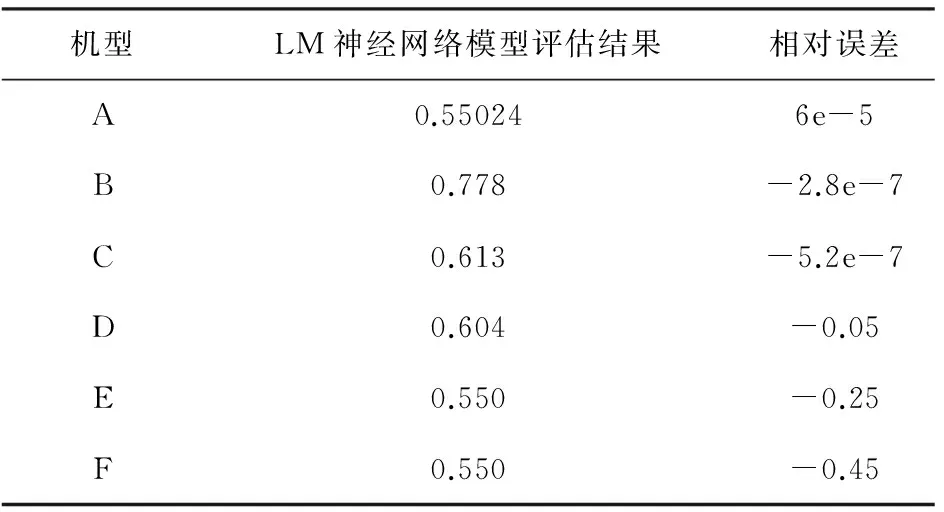
表5　基于LM算法的BP神经网络综合作战效能评估结果

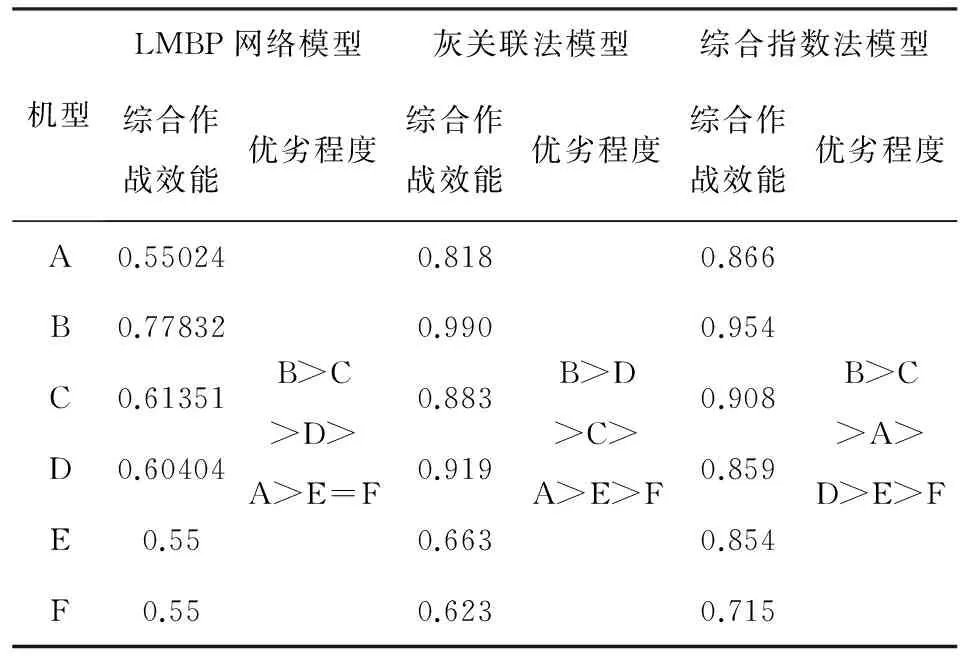
表6　三种模型综合作战效能评估结果

本文还采用灰关联法[8]、综合指数法[1]对战斗机综合作战效能进行了评估，其评估结果对比如表6所示。

表6数据表明，对于灰关联模型和本文所述的LMBP网络模型，二者虽然在机型C、D的排序上相反，但是仔细分析数据可以发现，LMBP网络模型所评估出的机型C、D之间的差值很小，故也可视为与灰关联法模型评估结果基本一致。而分析LMBP网络模型和综合指数法模型的评估结果可知，二者在机型A、D的排序上相反，但是根据相关评价及数据可知，机型D明显优于机型A，故综合指数法在机型A、D的排序上存在瑕疵，故可将此项忽略；从整体来看，综合指数法模型的排序与LMBP网络模型的排序是基本一致的。综上所述，三种模型评估的结果基本是一致的，说明了基于LM算法的BP神经网络用于评估战斗机综合作战效能是合理、可靠的。

不过，仔细观察表6中LMBP网络模型对机型E、F的评估数据，发现二者评估值相等，因此就本文给出的样本而言，该模型的评估区分性不是很好。这一般是由于训练样本不足、或者训练样本不够典型等原因造成的，因此后期可以在训练样本的选取上进行进一步的研究改进。

4　结语

本文融合战斗机空对空、空对地评估指标，构建了合理的评估指标体系。在此基础上，通过基于LM算法的BP神经网络建立了战斗机综合作战效能评估模型。最后对6种机型进行了综合作战效能评估，所得评估结果与已有文献提出的2种模型评估结果基本一致，说明了该模型是合理可靠的。

由于人工神经网络法是一种更为客观的方法，较好地回避了主观方法中的人为不利因素，例如无需人为加入权重，而是由网络根据数据随机调整神经元之间的权重、阈值，直至误差最小。同时，由于BP神经网络自身具有良好的泛化拟合能力，因此可以较好地处理样本中数据残缺、模糊等问题。而对于有瑕疵的数据，网络自身良好的容错能力也可以解决之。人工神经网络作为一种人工智能方法，其在综合作战效能方面的应用与研究，符合当下人工智能的发展趋势。但是，由于训练样本有限，因此本文训练所得神经网络模型并不是最佳的。后期若能获得数量充足、质量可靠的样本数据，将使得网络的评估精度大大提高，而输出结果的区分度也将会更加明显。

最后，本文效能评估建模思路和模型可以为其他类似研究提供参考。但是在指标的选取和训练样本的构造上需要依据实际情况进行一定修改。

[1] 董彦非，胡涛.战斗机综合作战效能评估建模方法[J].火力与指挥控制,2012,37(2)：9-11.

[2] 朱宝鎏,朱荣昌,熊笑非.作战飞机效能评估[M].2版.北京：航空工业出版社,2006.

[3] 刘帅,寇英信,付昭旺,等.基于人工神经网络的空战效能评估[J].电光与控制,2010,17(4):26-29.

[4] Samarasinghe S.Neural Network for Applied Sciences and Engineering:From Fundamentals to Complex Pattern Recognition[M].Florida:CRC Press,part of Taylor & Francis Group LCC,2007:9,11-13,61,88,138.

[5] 黄国庆,王国良,藏青松.参数可调的战斗机空战效能评估系统研究[J].电光与控制,2013,20(2):33-36.

[6] 张素梅,黄天辰,彭灏.基于神经网络模型的武器装备作战效能评估[J].军事运筹与系统工程,2006,20(4):40-43.

[7] Ham F M.Kostanic I.Principle of Neuro-computing for Science and Engineering[M].New York:McGraw-Hill,2011:132.

[8] 刘思峰.灰色系统理论及其应用[M].5版.北京:科学出版社,2010:45-50.

[责任编辑、校对：李琳]

Synthesized Combat Effectiveness Evaluation of Fighter Planes Based on BP Neural Network by LM Algorithm

WuXin-peng,QuGao-min

(School of Aircraft,Xi'an Aeronautical University,Xi'an 710089,China)

Aiming at the multifunction and multi-use development trend of dual mission fighter planes,the synthesized combat effectiveness evaluation model for these planes is established by BP neural network using LM algorithm on the basis of effectiveness evaluation index system with air-to-air and air-to-ground combat requirements.The nonlinear relationship between indexes and effectiveness evaluation values is built via the favorable function fitting and predication ability of artificial neural network.Moreover,with the help of fault tolerant capability in artificial neural network,the problems are solved,such as incomplete or wrong sample data.Finally,6 planes are evaluated by using Matlab neural network tool to run this LMBP model.The evaluation values of the model processed in this paper are compared with those of other two,and the results verify the availability and rationality of this model.

fighter planes;synthesized combat effectiveness evaluation;LM algorithm;BP neural network

2016-06-29

陕西省自然科学基金(2016JM1014)；陕西省教育厅自然科学基金(16JK1396)

吴欣蓬(1993-)，男，浙江宁波人，西安航空学院飞行器学院，从事航空武器系统仿真、效能评估与效费分析研究。

V271.4；E926

A

1008-9233(2016)05-0012-08