无人机自主着陆高度控制系统设计研究
邹 凯,丁继成
(1.中国航天空气动力技术研究院,北京 100074; 2.哈尔滨工程大学 自动化学院,哈尔滨 150001)
无人机自主着陆高度控制系统设计研究
邹 凯1,丁继成2
(1.中国航天空气动力技术研究院,北京 100074; 2.哈尔滨工程大学 自动化学院,哈尔滨 150001)
无人机自主着陆是无人机任务执行后顺利回收的重要阶段;论文根据固定翼无人机着陆滑跑的特点,设计了无人机着陆滑跑的下滑高度轨迹及高度控制回路;在已知无人机着陆性能和空气动力学模型的情况下,根据无人机飞行任务的需求,研究了直线下滑段的轨迹设计,利用指数拉平方法设计了末端拉平段的轨迹,并结合PID控制技术对无人机的纵向俯仰控制回路以及整个无人机高度控制回路进行了建模和详细研究,利用MATLAB仿真技术对设计的控制方案的性能进行了详细分析,获得了相应的关键设计参数;对设计的高度控制回路方案的数学仿真和基于FlightGear飞行环境模拟系统的半物理仿真验证了所设计的自主着陆高度控制系统的可行性,具有一定的参考实用价值。
无人机着陆;PID控制;高度控制
0 引言
飞行控制系统能够控制无人机出色地完成任务,并实现无人机安全且完整的回收[1]。目前,常用的四种无人机回收方式有空中回收、降落伞回收、阻拦网回收以及滑跑降落回收[2-8]。前三种回收方式均需要额外的回收设备,对控制系统的控制性能要求低,但回收成本高,且在回收的过程中容易造成机身的损坏[1]。滑跑着陆回收具有无需额外设备和人员参与,机身无损伤,且降落后可立刻起飞等优点,因此,滑跑降落回收方式的成本更低,回收更方便。考虑到固定翼无人机在滑跑降落过程中进场平飞和轨迹捕获阶段的轨迹由巡航控制,在执行不同的飞行任务时,轨迹存在很大差异[9],不必进行统一设计,而只需对直线下滑和末端拉平阶段的轨迹及其控制系统进行统一设计。
1 无人机着陆轨迹设计
1.1 直线下滑段轨迹设计
无人机要实现安全着陆,必须在着陆过程中跟踪下滑轨迹线的高度剖面,而在直线下滑阶段,下滑轨迹角则决定了无人机下滑速度的可控性,为保证安全着陆,通常可考虑设置无人机的拉平决策高度为10米。本文以天行者1 680无人机为研究对象,该类型无人机具有重量轻和易受到侧风干扰的特点,需要较长的下滑轨迹以矫正下滑曲线。因此,文中选取下滑角γ=-2.5°的普通直线下滑。
1.2 末端拉平段轨迹设计
合理的拉平轨迹设计可将无人机的下滑垂直速度减小到允许的着地速度范围。在目前常用的拉平轨迹设计中,指数拉平轨迹较为成熟,易于实现且精度较高。它基于飞机瞬时下降速度与高度成比例的思想,在理想情况下,当飞机下降速度为零时,高度H(t)也应该等于零,即[10]:
(1)
由上述微分方程,可得
(2)

(3)
由上述微分方程,可得
(4)
令H(t1)=0,则拉平时间t1为:
(5)
在拉平过程中假设无人机的速度为常数,为避免拉平距离l无限长,可假设跑平面高出拉平轨迹渐近线hc的距离,则:
(8)

(9)
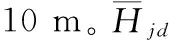
2 纵向俯仰控制回路设计与仿真
纵向控制回路以俯仰角控制回路为内回路,高度控制回路以俯仰角控制回路为基础搭建,作为纵向导航控制回路的外回路。俯仰角速率和俯仰角可由惯性测量单元(Inertial Measurement Unit, IMU)提供。同时引入俯仰角速率反馈,可增加无人机的纵向阻尼系数,减少俯仰控制回路的振荡。俯仰角反馈能够改善无人机的长周期模态的阻尼特性,提高系统的稳态精度。无人机俯仰控制律如图1所示。
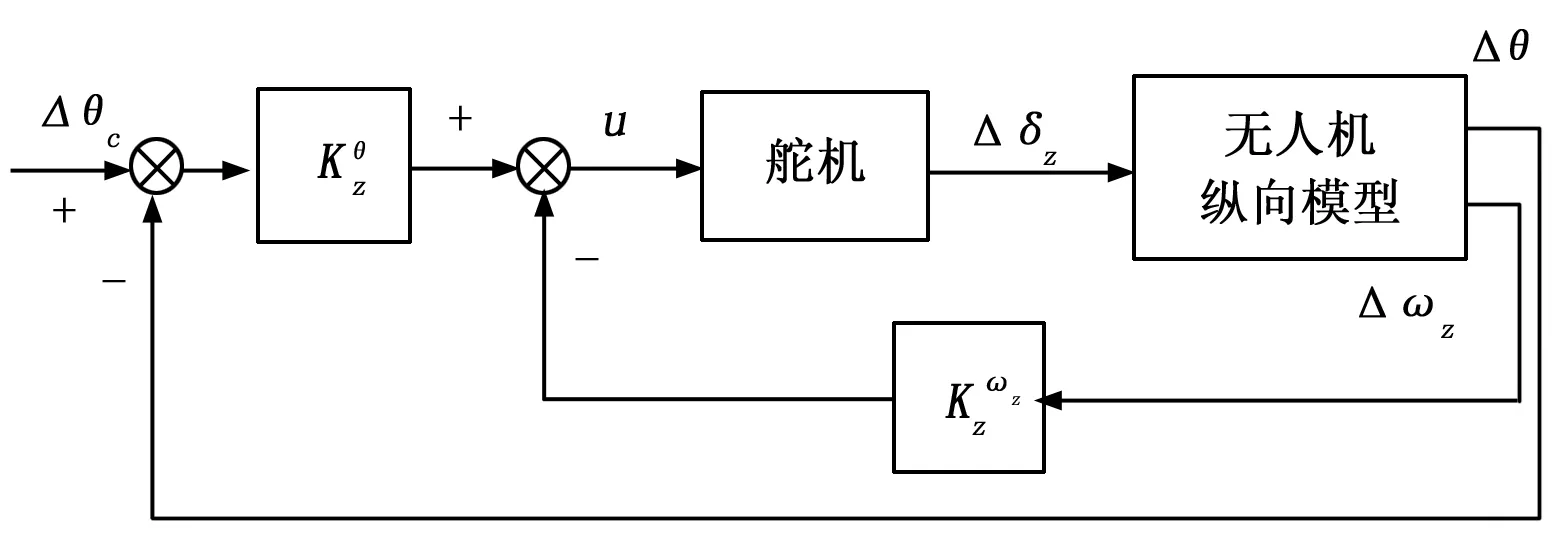
图1 俯仰角控制律
图1中,Δθc为期望俯仰角,Δθ为实际俯仰角,Δωz为俯仰角速率。其控制表达式可以表示成:
(11)
当采用常规PID控制结构时:
(12)


(13)
式中,

B=[0,-0.0172,0,-5.2096,0]T
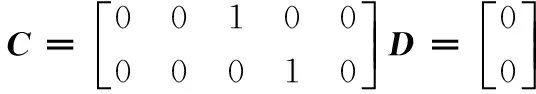

(14)
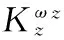
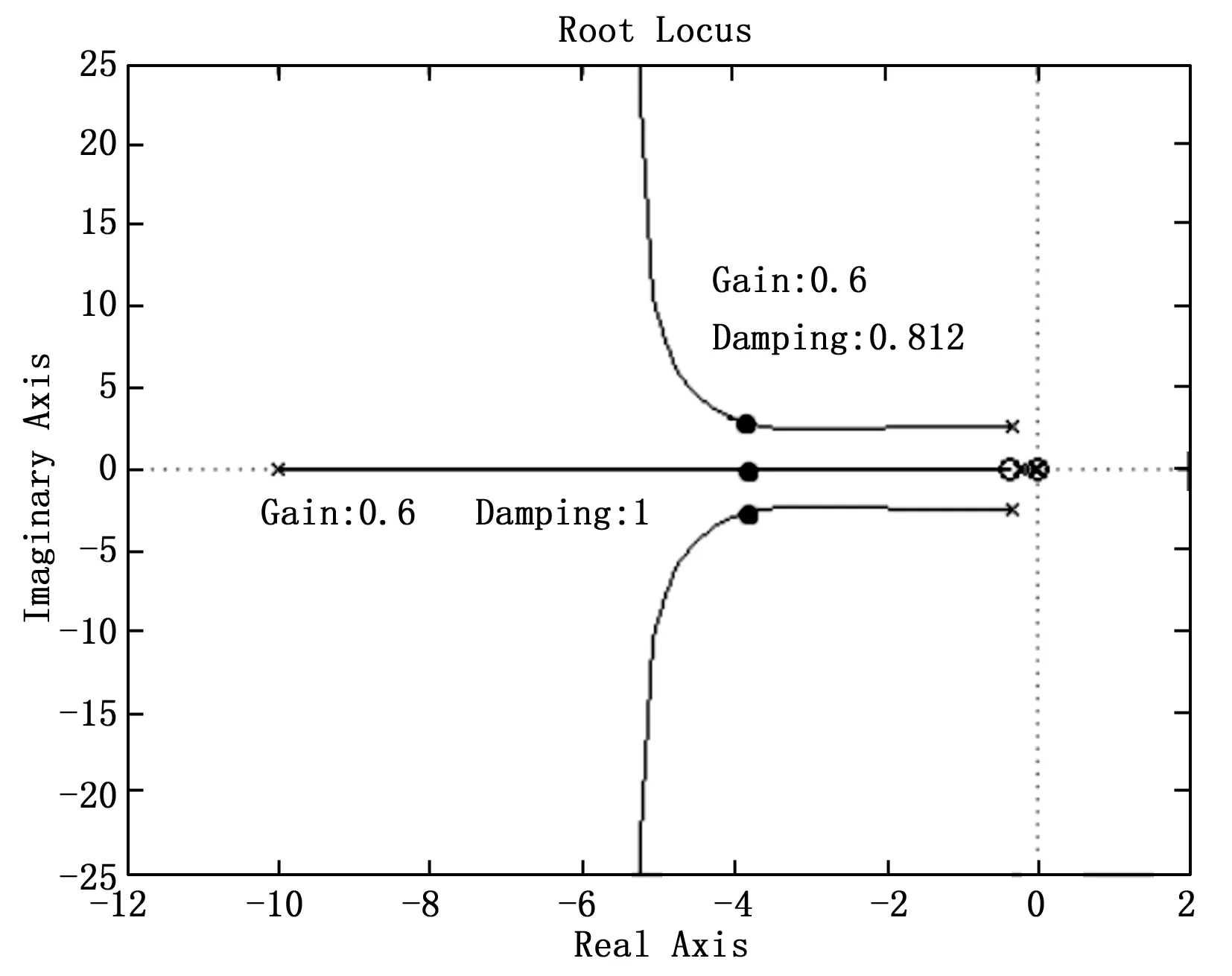
图2 俯仰角速率根轨迹
为整定PID控制参数,假设期望相角裕度φm=60°,截止频率ωc= 4rad/s,α=4。可得Kp=1.34,Tp=0.47,Ti=1.88。基于PID控制的俯仰角控制系统的仿真结果如图3所示。

图3 俯仰角阶跃响应曲线
由图可见,在设计的控制回路和PID参数情况下,系统具有快速调整特性和很小的超调,可满足俯仰角控制要求。
3 高度跟踪控制回路的设计与仿真
为使无人机快速跟踪下滑轨迹,本文采用控制升降舵的方法实现高度控制系统的设计。设计的高度控制律如图4所示,图中ΔHc为期望的飞行高度偏差,ΔH为测量得到的高度偏差。

图4 高度控制律
高度偏差信号与高度变化率信号反馈可实现飞行过程中高度阶跃响应的要求,但在高度保持飞行中无法克服静差,因此在高度控制回路中加入积分环节,以保证无人机无静差的飞行。无人机高度控制回路的控制率可采用如下公式表示:
(15)
在设计基于PID控制的无人机高度控制系统时,只需保持原有所设计的俯仰姿态回路不变,然后在此基础上设计基于PID控制的高度保持/控制外回路。无人机着陆段的高度剖面的仿真跟踪曲线如图5所示。

图5 轮式无人机自主着陆高度剖面跟踪曲线
从图中可以看出,测试无人机在下滑初期跟踪误差较大,原因在于,此时无人机尚未进入着陆程序,未建立下滑角,在达到下滑初始高度50m以后,建立下滑角,此后无人机能够较好地跟踪高度曲线,在达到拉平决策高度后的末端拉起段,考虑到发动机停车会导致轻质飞机姿态随环境改变,着陆点与理论着陆点会存在一定的偏差,该偏差在15m之内。
4 半物理仿真验证
为进一步验证控制系统的可用性,用于验证的半物理仿真实验平台环境如图6所示。图中,台式计算机运行飞行模拟软件,用于模拟并输出飞机的各项飞行状态数据和执行自动驾驶仪给出的控制信息;笔记本电脑运行无人机地面站软件,用于无人机飞行任务规划及飞行状态显示;方框内为无人机飞行控制系统硬件,采用AtmelMega2560芯片作为控制核心,飞行控制系统内部包含本文所设计的高度控制方案。

图6 半物理仿真环境 图7 无人机航迹线
FlightGear仿真软件基于真实的环境和飞机模型搭建,其输出的位置信息与真实的环境位置信息一致。为增加半物理仿真的真实性并验证无人机导航控制回路的抗干扰能力,将环境风力设定为3级,风向随机生成并随时间不断变化,以增加飞行难度。
无人机航迹线如图7所示。设计方案的半物理仿真高度跟踪结果如图8所示,图8中相位超前的梯形直线为无人机任务规划过程高度,由9个预设航点的规划出期望的高度曲线。相位迟后的不规则曲线为无人机实际飞行的高度曲线。由于无人机在转弯过程中会损失高度,而且考虑到无人机机身不足2kg,加上侧风的影响,曲线中间段的高度存在波动,同时,在转弯损失高度后,需要高度控制回路对高度进行补偿,因而无人机的高度跟踪有一定的迟后,但仍然能够控制无人机完成航迹跟踪。
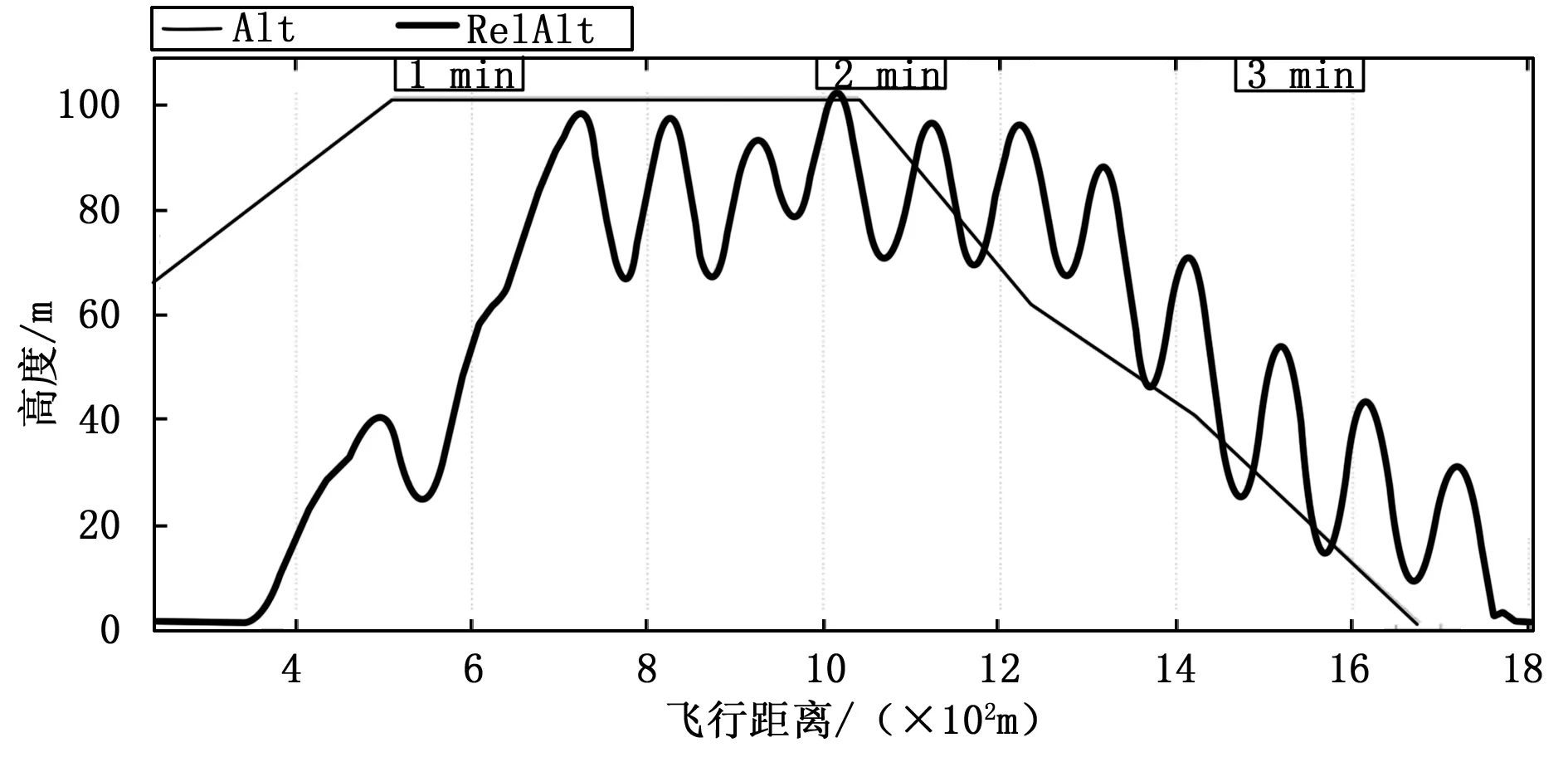
图8 高度跟踪曲线
5 结论
本文对无人机的着陆轨迹和纵向控制回路进行了设计与建模,在理论方面设计了小型无人机指数下滑曲线和控制模型的建立,消除了机身俯仰控制的无阻尼震荡,同时确保了高度调节的快速性,完成了无人机自主着陆纵向高度控制的数学仿真与半物理仿真验证,具有一定的参考价值。
[1] 淳于江民,张 珩.无人机的发展现状与展望[J].飞航导弹,2005(2):23-27.
[2]Sasiadek,HartanaP.Sensorfusionfornavigationofanautonomousunmannedaerialvehicle[A].RoboticsandAutomation.Proceedings,ICRA'04, 2004IEEEInternationalConferenceon[C]. 2004: 4029-4034.
[3] 张 勇,徐贵力,章凤翎,等.无人机自主着陆过程中合作目标特征点的提取方法研究[J].航空兵器,2010(1):25-28.
[4] 张剑锋,刘秉华,贾彩娟.无人机自主着陆控制[J].控制理论与应用,2009, 26(12):1383-1386.
[5] 陈 海.无人机自主控制综述及自主着陆控制系统设计[D]. 西安:西北工业大学, 2007.
[6] 何湘智,王荣春,罗倩倩.固定翼无人机纵向控制律设计及仿真验证.科学技术与工程[J], 2010,10(9):2134-2138.
[7]GuiliXu,YongZhangSheng.Researchoncomputervision-basedforUAVautonomouslandingonaship[J].PatternRecognitionLetters, 2009, 30: 600-605.
[8]TsaiChiyi,SongKaitai,XavierDutoit,etal.Robustvisualtrackingcontrolsystemofamobilerobotbasedonadual-Jacobianvisualinteraction[J].RoboticsandAutonomousSystems, 2009,57: 652-664.
[9] 胡 勇.信息融合技术在无人机中的应用研究[D]. 南京:南京航空航天大学, 2008.
[10] 肖业伦.飞行器运动方程[M]. 北京:航空工业出版社, 1987.
Research of Height Control Technique on UAV Automatic Landing
Zou Kai1, Ding Jicheng2
(1.China Academy of Aerospace Aerodynamics, Beijing 100074, China;2.College of Automation, Harbin Engineering University, Harbin 150001, China)
In order to achieve the small UAV automatic landing on UAV research project, an UAV automatic landing-vertical height control strategy was provided. According to the UAV flight mission requirements, the aircraft landing performance and aerodynamic model, the design of the straight line sliding trajectory was researched. Besides, an index leveled method has also been used to design the glide path. The PID control techniques has been used to design a reasonable vertical and pitch control loop model, as well as high control loop model. Some necessary performance analysis and critical parameters selection has been finished by MATLAB simulation. After completed the design of UAV control system, a principle simulation based on MATLAB and hard-in loop simulation based on FlightGear flying environment simulator validate the efficacy and practicability of the flight high control strategy. This can be as a reference for UAV high control loop design.
UAV landing; PID control; UAV height control
2015-11-11
2016-01-29。
国家自然科学基金(61304234,61273081);中央高校基本科研业务费专项资金资助(HEUCFX041403)。
邹 凯(1988-),男,哈尔滨人,工学硕士,工程师,主要从事无人机导航、制导与控制方向的研究。
1671-4598(2016)07-0090-03
10.16526/j.cnki.11-4762/tp.2016.07.024
TP271 文献标识码:A

