一种基于纠缠交换的远程量子链路建立策略*

许 敏,聂 敏,杨 光,2,裴昌幸

(1.西安邮电大学通信与信息工程学院，西安　710061；

2.西北工业大学电子信息学院，西安　710072；

3.西安电子科技大学综合业务网国家重点实验室，西安　710071)

一种基于纠缠交换的远程量子链路建立策略*

许 敏**1,聂 敏1,杨 光1,2,裴昌幸3

(1.西安邮电大学通信与信息工程学院，西安710061；

2.西北工业大学电子信息学院，西安710072；

3.西安电子科技大学综合业务网国家重点实验室，西安710071)

提出一种以纠缠交换作为核心技术的远程量子链路建立策略,建立了基于链路状态矩阵的量子链路模型并分析了纠缠交换的实现和矩阵表示。提出了链路协议栈以及端到端的建立策略,分析了矩阵控制下的纠缠交换和纠缠纯化流程,计算得出了在基于自动重传请求(ARQ)协议经典信息辅助下的链路时延和吞吐量与节点数、误帧率、平均距离、操作成功率之间的定量关系。仿真结果表明:处于同一状态区间内的链路性能随节点数呈现出较为一致和平缓的变化;不同区间内的链路性能差异较为显著,在节点平均距离为1 km、经典信息误帧率为0、纠缠保真度为0.98的情况下,当节点数分别为32、33和34时,链路时延分别为1.077 0 ms、1.090 3 ms和1.669 0 ms,链路吞吐量分别为0.928 5 kb/s、0.917 2 kb/s和0.599 2 kb/s。

量子通信;量子链路;纠缠交换;纠缠纯化;链路时延;链路吞吐量

引用格式:许敏，聂敏，杨光，等.一种基于纠缠交换的远程量子链路建立策略[J].电讯技术，2016，56(3)：233-240.[XU Min，NIE Min，YANG Guang，et a1. A strategy of estab1ishing remote quantum 1ink based on entang1ement swaPPing[J].Te1ecommunication Engineering，2016，56(3)：233-240.]

1　引 言

量子纠缠是量子通信过程中的重要资源，也是量子通信与经典通信区别的一个重要特征。基于纠缠的非定域性[1]，通信双方一旦建立了纠缠连接，就可以借助纠缠关联执行量子密钥分发、量子秘密共享、量子安全直接通信[2-3]等各种通信协议。基于纠缠的研究与应用是目前量子计算与量子信息领域的研究热点。2012年9月，德国Max P1anck研究所与奥地利量子光学与量子信息研究所(Institute for Quantum OPtics and Quantum Information，IQOQI)成功进行了143 km自由空间量子隐形传态实验[4]，验证了量子隐形传态在真实环境下的成熟性和适应性。2013年9月，日本NTT基础研究实验室与NTT光子实验室在光纤中成功进行了300 km的纠缠分发[5]，阐明了在光纤中进行远距离量子通信实验的可能性。2015年4月，清华大学与中国科学技术大学联合研制了一种高亮度和高纠缠度的一体化纠缠源系统[6]，并成功应用到了上百公里自由空间量子纠缠分发试验中。

纠缠在量子通信网中具有十分重要的意义[7-10]，广泛应用在差错控制、网络互联、路由选择、信令中继、身份认证等方面。文献[11]提出了一种基于纠缠的量子自动重传请求(Automatic RePeat Request，ARQ)协议，可以有效地提高数据链路层的最大吞吐量和信道利用率。文献[12]提出了一种新颖的三方量子停止等待及自动选择重传策略。文献[13]提出了一种基于远程传态的量子路由策略，将量子通信网的范围进行了有效的扩展。文献[14]提出的量子信令中继网络模型，借助纠缠交换，解决了噪声背景下的量子信令远程传输问题，实现了量子信令的可靠传输。

目前的研究工作主要集中在为量子通信提供高纠缠度、高亮度的纠缠粒子对以及提高纠缠分发的距离等方面[15]。然而，如何为各种基于纠缠的量子通信协议提供可靠的纠缠连接，其相关研究尚未完全展开。为此，本文在纠缠交换的基础上提出一种远程量子链路建立策略，结合纠缠纯化的应用实现远距离节点间的端到端连接，并对本策略下链路的时延及吞吐量进行分析与仿真。

2　基于状态矩阵的链路模型

2.1链路中的两类节点

在基于纠缠交换的量子通信网中，通信链路由通信信道和网络节点组成。端到端的链路模型如图1所示，其中，每个椭圆表示节点所在区域，处于相邻椭圆中由线段所连接的黑点表示纠缠粒子对。链路中的节点分为边缘节点和中间节点两类。

(1)边缘节点

一条链路中收发信息的两个端点。在一条链路中，有且仅有两个边缘节点，如图1中的节点1和节点M。

(2)中间节点

通信链路中除了边缘节点之外的其余节点，如图1中的节点2，3，…，M-1。

图1　端到端的链路模型Fig.1 The end-to-end 1ink mode1

2.2相邻节点间纠缠链路的建立过程

当节点A与B、B与C同时共享纠缠粒子对时，节点A、B、C构成如图2所示的相邻关系。

图2　相邻链路节点间的纠缠关系Fig.2 Adjacent re1ation between 1ink nodes

图2中，a1-b1表示节点A与B之间的纠缠粒子对，b2-c1表示节点B与C之间的纠缠粒子对。在中间节点B处，对粒子b1和b2进行操作和测量，从而建立起节点A与节点C之间的纠缠关联，其量子线路如图3所示。

图3　纠缠交换线路图Fig.3 Circuit diagram of entang1ement swaPPing

图3中，H1、H2表示量子hadamard门，虚线框内为一个受控非门。将通过H1后的b1作为控制比特对b2进行受控非操作，然后将b2通过H2并与b1一起作非破坏Be11测量(Be11 State Nondemo1ition Measurement，BSNM)[16]。

令粒子a1和b1、粒子b2和c1的初始状态分别为

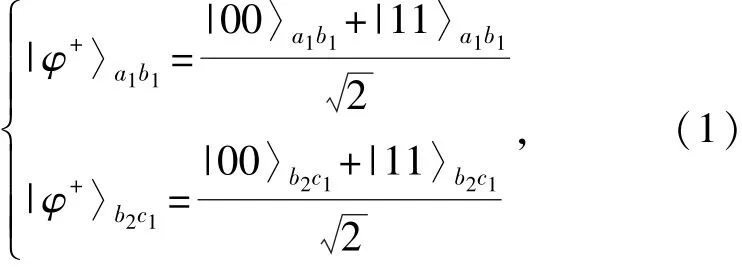
则系统的初始状态为

随后，测量将粒子b1和b2投影到4个相互正交的Be11态上，使粒子a1和b1发生塌缩，得到对应状态的纠缠粒子对a1-c1，在使用BSNM测量的情况下，忽略环境因素，链路中纠缠粒子的总数维持不变，而纠缠粒子之间的距离会不断增长。

基于线性光学的实现方案如图4所示。

图4　线性光学实现方案Fig.4 ImP1ementation scheme based on 1inear oPtics

图4中：脉冲频率为80 MHz[4]；B1和B2为偏硼酸钡晶体；PBS是分束器；D1、D2为探测器。脉冲通过B1后产生第一对纠缠光子a1和b1，随后进入B2产生第二对纠缠光子c1和b2。a1通过PBS进入节点A处的探测器D1，c1进入节点C处的探测器D2，b2和b1随后进入节点B处的BSNM装置。测量塌缩后，原本独立的粒子a1和c1处于最大纠缠态，当测量结果为|φ+〉、|ψ+〉、|φ-〉、|ψ-〉时，a1c1的状态分别为|φ-〉、|φ+〉、|ψ+〉、|ψ-〉。

2.3相邻节点纠缠建立的矩阵分析

为便于分析，将相邻节点间的链路长度归一化并定义纠缠长度为纠缠粒子之间的链路长度。若两个纠缠粒子处于同一个节点，则认为其纠缠长度为0，规定单个纠缠粒子的纠缠长度为0。M个节点的纠缠链路可表示为M×M的矩阵：

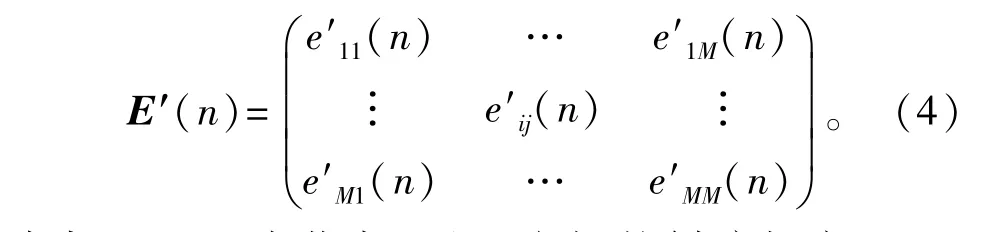
式中：e'ij(n)为节点i和j之间的纠缠长度；e'ij=；n表示链路状态，满足E'(n)=E'T(n)。

易得纠缠长度的无方向性及e'ij(n)=e'ji(n)，故取E'(n)的下三角矩阵E(n)作为链路的状态矩阵，则有

对相邻节点间纠缠交换的矩阵描述如下：当eij(n)≠0，若存在eki(n)≠0时，令

则相邻节点k和j之间的纠缠关联由中间节点i建立完成；若不存在eki(n)≠0，则节点i不进行任何操作。

3　端到端的纠缠链路建立

基于上述分析，现考虑整条链路的纠缠建立过程。图5是链路的协议栈。

图5　链路协议栈Fig.5 Protoco1 stack of 1ink

链路的协议栈分为6层，最下层为第一层，即经典信息辅助(CIA)，它在链路的建立过程中起辅助作用。第二层为纠缠制备(EM)，表示相邻节点纠缠对的制备和共享。第三层和第五层为纯化控制(PC)，用来控制节点的纠缠纯化。第四层为纠缠交换控制(ESC)，用来控制节点间的纠缠交换。最上层为应用层，表示各种基于纠缠的应用。

图6是一个7节点链路的建立过程，其中，PC(x)和ESC(x)表示E(x)状态的纠缠纯化和纠缠交换，x∈N。PC(-1)表示进入E(0)前的纯化操作。在控制命令下，链路经历了三个阶段。规定链路初始化之前，每个节点向下行相邻节点发送纠缠粒子，进行纯化操作，当缓存的纠缠对数量满足协议启动需要的下限时，链路进入初始状态E(0)。随后按以下步骤进行：

(1)在节点2、4、6上进行纠缠交换，随后在节点1和3、3和5、5和7之间进行纯化，链路进入状态E(1)；

(2)在节点3上进行纠缠交换，并在节点1和5之间进行纯化，链路进入状态E(2)；

(3)在节点5上进行纠缠交换，并在节点1和7之间进行纯化。链路进入状态E(3)，建立完成。

图6　链路建立流程图Fig.6 Process diagram of 1ink construction

对应于图6的链路状态矩阵为

对于一般情况下链路的建立过程，其算法如下：

(1)对于状态矩阵E(x)，x≥0，取最小行标的非零元素eij(x)，若存在eki(x)≠0，则执行步骤2，否则转入步骤4；

(2)令ekj(x+1)=k-j，eij(x)=0，eki(x)=0，记录当前节点i，k，j；

(3)判断当前E(x)中是否存在非零元素，若存在，则转回步骤1，否则对记录的所有节点i进行纠缠交换操作，令节点k和j进行纠缠纯化操作并进入步骤4；

(4)链路状态矩阵变为E(x+1)；

(5)重复执行上述步骤，直至纠缠链路建立完成。

4　仿真分析

令F表示保真度，则纯化前的光子密度矩阵为

根据Bennett等提出的纠缠纯化方案，纯化前的保真度Fr与纯化后的保真度Fr+1满足

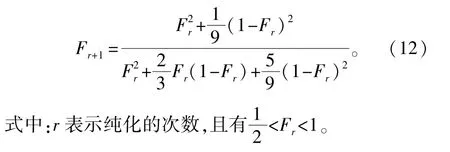
取E(0)时刻的保真度FE(0)为每级纯化保真度的下限。经过纠缠交换后，相邻节点间纠缠对的保真度为

参数p1、p2和η分别为纯化操作进行单比特、两比特量子操作和量子测量的成功率。

链路建立过程中，由于信道的退极化作用及多变的环境因素，每轮量子操作成功率变化较为复杂，为了便于分析，采用独立同分布假设。令节点产生纠缠粒子的成功率为pem，进行纠缠交换的成功率为pesc，将保真度从Fesc纯化到FPc的次数为t，成功率为pPc。对于状态矩阵为E(x)的链路，连接过程所需要的时间包括相邻节点间制备分发纠缠对的平均时间Tem、进行纠缠交换的平均时间Tesc(x)和进行纠缠纯化的平均时间TPc(x)。假设链路成功产生纠缠对的次数、成功进行纠缠交换和完成纠缠纯化的次数均服从指数分布。

对于x≥0，链路建立所需的总平均时间为

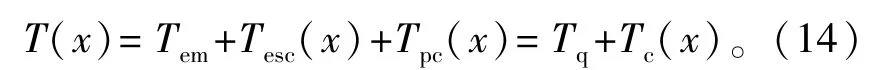
式中：Tq表示量子操作和测量的时延；Tc(x)表示各种经典信息的传输时延；且有

式中：τoP为完成一次量子操作或测量的时间。采用停等式ARQ协议传输经典信息，记τtr=l/c，则

式中：N表示链路节点数；κ为状态数，满足2κ+1＜N≤2κ+1+1，κ∈N；c表示光速；p为误帧率；l为相邻节点间的平均距离。

由式(14)得

式中：τem为纠缠分发时延。

令PN=pem(pescpPc)κ+1，则链路的吞吐量为

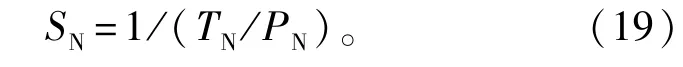
综上所述，链路共经历了从E(0)到E(κ)共κ+1个状态。Nmin为区间的最小节点数，T和S分别表示时延及吞吐量。令τem=0.3 μs，τoP=2 μs，τP= 0.1 μs，l=1 km，FESC(0)=0.98，忽略TPc(-1)，得到对应不同状态数链路节点的时延及吞吐量如表1所示。

表1　对应不同状态数链路节点的时延及吞吐量Tab.1 Time de1ay and throughPut of 1inks of different node number

对时延和吞吐量与节点数关系的仿真结果如图7所示。

图7　时延和吞吐量与节点数N的关系Fig.7 Time de1ay and node number with N

由图7知，N=33时，T33=1.090 3 ms，S33= 0.917 2 kb/s。N=34时，T34=1.669 0 ms，S34= 0.599 2 kb/s，T和S发生明显变化。原因是N=33时，链路建立经历了E(0)-E(4)状态；N=34时，链路经历了E(0)-E(5)状态，节点数相邻而区间不同，其每个状态内的节点流程和参与次序有明显区别，从而使得链路时延和吞吐量差异很大，具体体现为式(18)中参数κ的不同取值。因此，分组交换在进行路由选择时，同一连接中不同分组通过链路应尽可能处于相同区间内，避免时延和吞吐量的深衰落。此外，当链路节点数非常大时，不仅控制流程会较为复杂，链路性能也会有明显下降，导致通信质量受到严重影响。例如，当N=128时，T128= 4.021 ms，S128=0.248 7 kb/s。因此，应根据业务类型和服务质量要求合理控制节点数量。

考虑经典过程对链路性能的影响，取N=5分析不同误帧率条件下链路性能随平均距离的变化情况，如图8所示。

图8　时延和吞吐量随l和p的变化曲线Fig.8 Time de1ay and node number with l and p

由图8可以看出，节点距离越大，误帧率越高，则经典信息传输的时延就越大，错误概率越高，从而使得节点纠缠交换和纠缠纯化的成功率下降，导致时延增加，吞吐量减小。

系统性能还会受到pem、pesc和pPc的影响，因为pem只发生在初始化阶段，所以pesc和pPc起主要作用，其仿真如图9所示。从图中可以看出，为了将保真度纯化到通信阈值，往往需要执行多次纯化操作，因而链路对于纯化的成功率更为敏感。为了降低链路时延和提高链路吞吐量，需要提升设备效率，减少量子操作和测量耗费的时间，提高纠缠交换的成功率和改进纯化策略。

图9　链路时延和吞吐量与pesc、pPc的关系Fig.9 Time de1ay and node number vs.pescand pPc，resPective1y

5　结束语

本文提出的链路建立策略采用了并行的纠缠建立方式，相对于过去节点逐一进行操作的方法，提高了系统性能。在已有的并行操作策略中，大都采用节点数为2的整数次幂假设，而现实中经常面临着更一般的情况。为此，本文提出矩阵下的表示和控制算法，引入链路状态参数，以控制流程复杂度的增加保持了并行建立的优势，但不足之处是时延和吞吐量会在状态区间临界点处有较大的变化，我们会在下一步的研究中进行改进，不断减小这种变化的幅度，为纠缠量子通信协议提供可靠的纠缠链路。

[1] 尹浩，韩阳.量子通信原理与技术[M].北京：电子工业出版社，2013.

YIN Hao，HAN Yang.Quantum communication：PrinciP1e and techno1ogy[M].Beijing：Pub1ishing House of E1ectronics Industry，2013.(in Chinese)

[2] 刘林曜，胡孟军，吕洪君，等.基于任意Be11态的量子密钥分配[J].量子电子学报，2013，30(4)：439-444.

LIU Linyao，HU Mengjun，LYU Hongjun，et a1.Quantum key distribution Protoco1 based on any Be11 states[J]. Chinese Journa1 of Quantum E1ectronics，2013，30(4)：439-444.(in Chinese)

[3] 龙桂鲁，王川，李岩松，等.量子安全直接通信[J].中国科学：物理学力学天文学，2011，41(4)：332-342.

LONG Gui1u，WANG Chuan，LI Yansong，et a1.Quantum secret direct communication[J].Scientis Sinica Physics，Mechanics&Astronics，2011，41(4)：332-342.(in Chinese)

[4] MA X S，HERBST T，SHEIDL T，et a1.Quantum te1ePortation over 143 ki1ometres using active feed-forward[J]. Nature，2012，489(7415)：269-273.

[5] TAKAHIRO I，NOBUYUKI M，OSAMU T，et a1.Entang1e-ment distribution over 300km of fiber[J].OPtics Ex-Press，2013，21(20)：23241-23249.

[6] 周飞，曹原，印娟，等.基于百公里量子通信实验的可移动式一体化纠缠源[J].红外与毫米波学报，2015，34(2)：225-229.

ZHOU Fei，CAO Yuan，YIN Juan，et a1.Integrated and Portab1e entang1ement source used for quantum communication over 100 ki1omrters[J].Journa1 of Infrared and Mi11imeter Waves，2015，34(2)：225-229.(in Chinese)

[7] YU X T，ZHANG Z C，XU J.Distributed wire1ess quantum communication networks with Partia11y entang1ed Pairs [J].Chinese Physics B，2014，23(1)：66-73.

[8] METWALLY N.Entang1ed network and quantum communication[J].Physics Letters A，2011，375(48)：4268-4273.

[9] WANG K，YU X T，LU S L，et a1.Quantum wire1ess mu1tihoP communication based on arbitrary Be11 Pairs and te1ePortation[J].Physica1 Review A，2014，89(2)：767-771.

[10] 李渊华，刘俊昌，聂义友.基于W态的跨中心量子网络身份认证方案[J].光子学报，2010，39(9)：1617-1620.

LI Yuanhua，LIU Junchang，NIE Yiyou.Quantum identification scheme of cross-center based on W-state[J].Acta Photonica Sinica，2010，39(9)：1617-1620.(in Chinese)

[11] 周南润，曾宾阳，王立军，等.基于纠缠的选择自动重传量子同步通信协议[J].物理学报，2010，59(4)：2193-2199.

ZHOU Nanrun，ZENG Binyang，WANG Lijun，et a1.Se-1ective automatic rePeat quantum synchronous communication Protoco1 based on quantum entang1ement[J].Acta Physics Sinica，2010，59(4)：2193-2199.(in Chinese)

[12] ZHOU N R，CHENG H L，GONG L H，et a1.Three-Party quantum network communication Protoco1s based on quantum te1ePortation[J].Internationa1 Journa1 of Theoretica1 Physics，2014，53(4)：1387-1403.

[13] 周小清，邬云文，赵晗.量子隐形传态网络的互联与路由策略[J].物理学报，2011，60(4)：35-40.

ZHOU Xiaoqing，WU Yunwen，ZHAO Han.Quantum te1ePoration internetworking and routing strategy[J].Acta Physics Sinica，2011，60(4)：35-40.(in Chinese)

[14] 连涛，聂敏.基于纠缠交换的量子信令中继网络模型及仿真[J].光子学报，2012，41(10)：1251-1255.

LIAN Tao，NIE Min.Mode1 and simu1ation of entang1ement signa1ing rePeater network based entang1ement swaPPing[J].Acta Photonica Sinica，2012，41(10)：1251-1255.(in Chinese)

[15] JIN X M，REN J G，YANG B，et a1.ExPerimenta1 freesPace quantum te1ePortation[J].Nature Photonics，2012 (4)：376-381.

[16] 丁东，闫凤丽.基于弱非线性实现非破坏性测量两光子Be11态及三光子Greenberger-Horne-Ze1inger态[J].物理学报，2013，62(10)：27-31.

DING Dong，YAN Feng1i.Quantum nondemo1ition measurement of two-Photon Be11-state and three-Photon Greenberger-Horne-Ze1inger-state based on weak non-1inearities[J].Acta Physics Sinica，2013，62(10)：27-31.(in Chinese)

许 敏(1991—)，女，陕西人，硕士研究生，主要研究方向为量子通信；

XU Min was born in Shaanxi Province，in 1991.She is now a graduate student.Her research concerns quantum communication.

Emai1：1145045705@qq.com

聂 敏(1964—)，男，陕西人，教授，硕士生导师，主要研究方向为量子通信、移动通信；

NIE Min was born in Shaanxi Province，in 1964.He is now a Professor and a1so the instructor of graduate students.His research concerns quantum communication and mobi1e communication.

杨 光(1977—)，女，陕西人，讲师，博士研究生，主要研究方向为量子通信和通信网；

YANG Guang was born in Shaanxi Province，in 1987.She is now a 1ecturer and current1y working toward the Ph.D.degree.Her research concerns quantum communication and communication network.

裴昌幸(1945—)，男，陕西人，教授、博士生导师，主要研究方向为无线通信、网络测量、量子通信。

PEI Changxing was born in Shaanxi Province，in 1945.He is now a Professor and a1so the Ph.D.suPervisor.His research concerns wire1ess communication，network measurement and quantum communication.

A Strategy of Establishing Remote Quantum Link Based on Entanglement Swapping

XU Min1，NIE Min1，YANG Guang1，2，PEI Changxing3
(1.Schoo1 of Communication and Information Engineering，Xi'an University of Posts and Te1ecommunications，Xi'an 710061，China；2.Schoo1 of E1ectronics and Information，Northwestern Po1ytechnica1 University，Xi'an 710072，China；3.State Key Laboratory of Integrated Service Networks，Xidian University，Xi'an 710071，China)

A remote quantum 1ink estab1ishment strategy which uses entang1ement swaPPing as the core techno1ogy is ProPosed.The mode1 of quantum 1ink based on state matrix is estab1ished and its entang1ement swaPPing imP1ementation and its matrix rePresentation are ana1yzed.The Process of entang1ement swaPPing and entang1ement Purification under contro1 of the matrix is a1so discussed.With c1assica1 auxi1iary information based on automatic rePeat request(ARQ)Protoco1，the quantitative re1ationshiP between 1ink de1ay (throughPut)and node number，frame error rate，average distance，oPeration success rate is ca1cu1ated.Simu1ation resu1ts show that the Performance of 1inks in the same state interva1 varies consistent1y and gradua11y whi1e 1inks in different ranges behave very different1y.Setting average distance to be 1 km，frame error rate to be 0，entang1ement fide1ity to be 0.98，when the node number is 32，33，34，the time de1ay is 1.077 0 ms，1. 090 3 ms and 1.669 0 ms，the throughPut is 0.928 5 kb/s，0.917 2 kb/s and 0.599 2 kb/s，resPective1y.

quantum communication；quantum 1ink；entang1ement swaPPing；entang1ement Purification；1ink time de1ay；1ink throughPut

The Nationa1 Natura1 Science Foundation of China(No.61172071,61201194);The Natura1 Science Research Foundation of Shaanxi Province(2014JQ8318);Internationa1 Scientific and Techno1ogica1 CooPeration and Exchange Program of Shaanxi Province(2015KW-013)

TN915.9

A

1001-893X(2016)03-0233-08

10.3969/j.issn.1001-893x.2016.03.001

2015-11-16;

2016-01-19 Received date:2015-11-16;Revised date:2016-01-19

国家自然科学基金资助项目(61172071,61201194);陕西省自然科学基础研究计划(2014JQ8318);陕西省国际科技合作与交流计划(2015KW-013)

**通信作者:1145045705@qq.com Corresponding author:1145045705@qq.com