双聚类算法研究
李美航,黄英仁
(广东省华南师范大学,广东广州510006)
双聚类算法研究
李美航,黄英仁
(广东省华南师范大学,广东广州510006)
双聚类算法的出现促进了生物基因分析领域的发展,简单介绍双聚类算法的起源、概念、目的及主要模型,对现有主要模型的优势与不足进行分析,并对常用双聚类算法的实验方法进行概括。
双聚类;基因表达数据;CC算法;OPSM
0 引言
基因芯片与DNA微阵列技术的发展给生物领域带来了大量的基因表达数据,如何从这些数据中找出有用的信息成为众多研究人员研究的热点。这些数据通常都以矩阵的形式存储,在基因表达数据矩阵中,行代表基因,列代表实验条件,每个元素代表某个基因在给定实验条件下的表达水平。
为了有效的分析这些数据,聚类分析最早被应用于其中。但传统聚类分析有一个明显的缺陷,就是只能对一个维度上的数据进行全局聚类。大量的生物实验已经证明,参与细胞功能运作的可能只是部分基因。不同于传统聚类,双聚类可以对数据矩阵的行和列同时聚类,它可以找到数据矩阵中的局部模式,这些局部模式可以很好的体现出部分基因在部分实验条件下的异同。
1 双聚类模型
虽然传统的聚类算法在分析基因表达数据时展现出一定的效果,但是面对加速膨胀的数据规模,其在解决高维度,高噪声数据时暴露出的疲软及不适合寻找矩阵中的局部模式缺陷,双聚类算法慢慢得到青睐。在学术上,双聚类算法主要分为四种模型:①常数型双聚类;②行常量或列常量双聚类;③数值一致表达型双聚类;④一致演化型双聚类。
1.1常数型双聚类
Hartigan[1]为了找到常数型的双聚类,采用了一种直接划分的块聚类方法。这种块聚类算法把原始的数据分成一系列小矩阵,然后用方差评估每一个小矩阵。虽然Hartigan的目的是为了寻找常数型双聚类,同时他也提出了寻找行常量和列常量双聚类的可能性,他提到只要我们选择合适的评价函数去评价分块后的小矩阵,那么我们将有可能找到行列常量甚至数值一致表达型双聚类。
1.2行常量或列常量双聚类
在寻找行列常量双聚类时,除了上述提到的选择合适的评价函数的方法。另外一个简单的思想是把矩阵中的数值依照行或列进行数据的标准化处理,这样便可以把寻找行列常量的双聚类转化为寻找常数型的双聚类。Getz等[2]便是用这种思想提出了CTWC算法。
1.3数值一致表达型双聚类
相对于以上简单的常量型双聚类,大多数算法对于更为复杂的数值一致表达型双聚类稍显无措。Cheng and Church[3]在CC算法中提出了双聚类这个概念,创造性地用均方残基去衡量子矩阵中表达水平的一致性,它可以有效的找出数值一致表达型双聚类,并给出了相应的函数。函数定义如下:
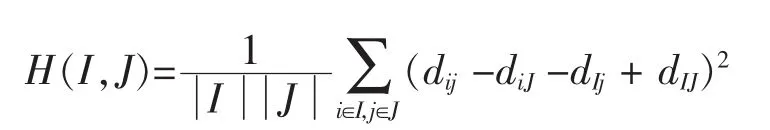
其中dij是当前元素值,dij表示第i行的行均值,dij表示第j列的列均值,dIJ=表示该子矩阵的总均值。
1.4一致演化型双聚类
随着双聚类算法研究的深入,越来越多算法聚焦于数据中的模式而非具体的数据元素值也就是一致演化型双聚类,它实际上是对数值一致表达型双聚类的一种放宽条件。最早由Bendor等[4]提出保序子矩阵模型(OPSM),它只关注元素值的相对大小而不理会实际值。OPSM双聚类模型本质上是一个基于模式的子矩阵,它的行在某种列置换情况下可以展示出严格的递增模式。一旦找到这样一种模式的双聚类,在生物基因学上可能揭示出某些共调控的基因在某些实验条件下有升降一致的体现,这对于研究基因在功能上的表现有很大的帮助。Bendor等人证明了寻找OPSM是NP-hard问题,并提出了一种贪心启发式算法用于挖掘具有统计学意义的OPSM。该算法从一些小的OPSMs出发,通过不断迭代去扩展这些OPSMs直到不能扩展为止。该算法能挖掘具有较大支持度阈值的OPSMs,但是它不能保证找到所有的OPSMs,并且需要较多的计算资源。
2 实验分析方法
双聚类算法已经广泛应用于基因表达数据,但如何去评估这些算法的优劣是一项具有挑战性的任务。目前主要从三个方面对算法性能进行综合评估:①双聚类结果的优劣;②算法对噪声数据的鲁棒性以及能否找到重叠的双聚类;③算法的可扩展性。目前所用的实验数据集主要来源于两方面,即真实数据集与人工合成数据集。
2.1真实数据集
在对双聚类结果的优劣进行评估时,我们会使用真实的数据集,目前双聚类实验中公认的几个真实数据集有:①酵母菌数据集[3],包含2884个基因和17个条件;②人类B细胞表达数据[5],包含4026个基因和96个条件;③乳腺肿瘤数据集[6],包含3226个基因和22个实验条件。算法在这些基因数据集上找到双聚类结果后,将对结果进行gene ontology(GO)(http://go. princeton.edu/cgi-bin/GOTermFinder)分析。GO分析被用来检验算法找到的双聚类的生物学意义,对产生的双聚类结果作真实性的验证。当某个结果在GO分析中有较小的P-value值,则说明该簇基因在某些细胞功能中有特别的生物意义。
2.2人工合成数据集
人工合成数据集由实验人员随机生成一个数据矩阵,再往该数据矩阵中嵌入不同的双聚类模型,不同噪声等级的双聚类,不同数量的双聚类或不同重叠度的双聚类。当用该合成数据运行算法得出结果后,可以对双聚类结果进行匹配分数计算[7],该匹配分数用来计算算法找到的双聚类结果与人工嵌入双聚类的匹配度,以此来衡量算法的性能。一般而言,算法的扩展性能评估由合成数据集测试,Gao等[8]在不断增加合成数据行、列和阈值数量的情况下,记录算法的运行时间,由此来评估该算法效率。
3 总结
双聚类是一个较为年轻的学术领域,在如今各种数据规模呈指数级别增长的年代,对它的研究有着重要的意义。本文主要介绍了双聚类在生物基因分析领域中的发展历程,许多其它新兴的领域(如数据挖掘,文本挖掘,推荐系统,电子商务等)都需要我们去探索与研究。
[1]Hartigan J A.Direct clustering of a data matrix.[J].Journal of the American Statistical Association,1972,67:123-129.
[2]Getz G,Levine E,Domany E.Coupled two-way clustering analysis of gene microarray data.[J].Proceedings of the national academy of sciences of the united states of america,2000:12079-12084.
[3]Cheng Y,Church G M.Biclustering of expression data.[J].In proceedings of the 8th International Conference on Intelligent Systems for Molecular Biology,2000:75-85.
[4]Ben-Dor A,Chor B,Karp R et al.Discovering local structure in gene expression data:the order-preserving submatrix problem.[J].In proceedings of the 6th international conference on computacional biology, 2002:49-57.
[5]Alizadeh A A,Eisen M B,Davis R E et al.Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling.[J].Nature,2000,403:503-511.
[6]Hedenfalk I,Duggan D,Chen Y et al.Gene-expression profiles in hereditary breast cancer.[J].New England Journal of Medicine, 2001,344(8):539-548.
[7]Preli?A,Bleuler S,Zimmermann P et al.A systematic comparison and evaluation of biclustering methods for gene expression data.[J].Bioinformatics,2006,22(9):1122-1129.
[8]Byron J G,Griffith O L,Ester M et al.On the deep Order-Preserving submatrix problem:a best effort approach.[J].Journal of IEEE Transactions on Knowledge and Data,2012,24(2):309-325.
李美航(1990-),男,硕士,研究方向为数据挖掘、双聚类分析;黄英仁(1992-),男,本科,研究方向为数据挖掘。
——卡文迪什测定万有引力常量

