移动荷载作用下柔性路面道路刚度计算分析∗

皮杰，丁建国

（南京理工大学理学院，江苏　南京　210094）

移动荷载作用下柔性路面道路刚度计算分析∗

皮杰，丁建国

（南京理工大学理学院，江苏南京210094）

要实现坦克、装甲车及高档民用车辆在道路行驶过程中的主动减振控制，首先需完成对道路刚度参数的快速计算。文中依据层状粘弹性理论体系建立柔性路面道路力学模型，采用ABAQUS有限元方法，对柔性路面道路刚度进行计算，并分析不同情况下柔性路面道路刚度的变化规律。结果表明，车速、车辆载重、温度和材料模量对柔性路面道路刚度的影响较大，当车速增大到临界速度时，道路刚度增大，车速继续增大则道路刚度减小；随着车辆载重和材料模量的增大，道路刚度总体呈增大趋势；随着温度的升高，道路刚度减小。

公路；柔性路面；道路刚度；层状粘弹性理论；移动荷载；有限元

高速公路的建设和使用，为车辆快速、高效、安全和舒适地运行提供了良好条件。目前，柔性路面的应用最为广泛，主要是因为柔性路面具有表面平整、没有接缝、行车平稳舒适、噪声小、施工周期短、成本低、维修方便等优点。随着交通的快速发展，各种民用高档汽车得到蓬勃发展，一般车辆自身配备的减振装置主要是靠预测汽车的运动特性来实现减振，无法实现主动减振。随着战场环境需求的不断提高，军用装甲车辆等装备的战斗技术指标也提高，在行进过程中，装甲类车辆会因自身发动机振动及路面起伏而引起车身振动，容易导致车内设备和零部件产生损伤而影响其正常运转，严重影响装备的行进速度和行进间射击精度。因此，需通过识别道路刚度，根据道路刚度调节车辆系统参数，实现车辆行驶过程中的主动减振。该文根据柔性路面道路设计参数计算道路刚度，为军用装甲车辆及民用车辆的主动减振控制提供基础条件。

柔性路面道路刚度计算，实质上是计算柔性路面的挠度值。由于路面层数往往超过3层，而且柔性材料中应力可传播范围有限，鉴于层状体系理论模型较接近实际柔性路面，针对柔性路面道路的研究大多基于层状弹性力学理论。常用的柔性路面地基模型有半无限空间地基和刚性地基两种。目前，利用有限元软件模拟移动荷载作用下柔性路面道路结构时大都采用二维模型，对三维模型的研究较少，而且大多局限于各向同性线弹性体，而对考虑面层弹塑性的柔性路面结构的研究较少。柔性道路的路基路面等材料具有粘弹性的特点，在移动荷载作用下介质本身的阻尼不可忽略，结构具有不可忽略的应变响应滞后和能量耗散等特点，因而粘弹性理论比弹性理论能更好地反映道路结构特性。在层数有限的情况下，采用联立求解方程组的方法可很好地对多层体系进行受力分析，但当路面结构层数较多时，所建立的方程增多，方程组也就很大，计算过程繁琐，计算量非常大，求解很困难。若再考虑柔性道路路基、路面材料的非线性影响，将其划分为十几甚至几十层，则几乎不可能求解其理论解。利用积分变换，采用传递矩阵的方法可解决上述问题，但需对结构进行大量简化。为了寻求移动荷载作用下柔性路面道路刚度的合理且精确的计算方法，该文参考弹性层状理论体系，考虑柔性路面道路的粘弹性特征，以粘弹性地基模型为基础，依据层状体系理论，利用ABAQUS有限元软件建立移动荷载作用下柔性路面道路的三维有限元模型，对柔性路面道路刚度的数值解展开研究。

1　柔性路面道路结构分析

1.1柔性路面道路的结构模型

柔性路面道路的路面结构，因其结构层是由不同材料构成，并且道路下方土体（路基）自身性质十分复杂，在外部荷载作用下其应力-变形关系一般呈非线性，其力学性质是非线性的弹-粘-塑性体。故采用半无限地基上层状粘弹性体模型（如图1所示）进行分析，并对路面结构作如下假设：

（1）各层都是由均质、理想的粘弹性（层状粘弹性体系为线粘弹性，材料参数的大小不随应力或应变的变化而改变）、各向同性的材料组成。

（2）土基在水平方向为无限大，在竖直方向为无限深，位于土基之上的各层结构的厚度均为有限，但水平方向为无限。

（3）路面面层上作用有荷载，在结构无限远及无限深处，应力和位移都为零。

（4）各层之间接触界面满足连续条件，具有相同的竖向应力和竖向位移，最下层无限深处应力和位移为零。

（5）不计自重。

图1　柔性路面结构力学模型

1.2车辆荷载作用模型

在对柔性路面道路结构进行力学分析时，针对车辆不同运动状态可对车辆荷载进行不同描述。将车辆荷载简化为移动的恒定荷载，当汽车匀速行驶时，假设汽车轮载为施加于面层上的均布垂直矩形荷载，荷载作用模型如图2所示。根据文献［13]将轮胎的接地面积近似为图3（a）所示的1个矩形和2个半径为0.3L的半圆的组合，将实际作用面积等效简化为矩形当量面积，长0.871 2L，宽0.6L［如图3（b）所示]。荷载作用长度L由式（1）确定：

式中：A为加载面积，可由每个轮胎承受的荷载P除以胎压p求得，即A=P/p。

图2　荷载作用模型

图3　单轮接地面积示意图

2　柔性路面道路有限元模型

2.1模型参数

柔性路面道路是三维体系的工程结构物，所承受的荷载亦是任意形式的，以三维有限元模型来描述路面体系比二维模型更合理，故采用ABAQUS有限元程序建立移动荷载作用下柔性路面道路三维有限元模型。为了验证该模型的正确性，采用文献［15]中的工程实例，其主要设计参数如表1所示。

表1　某柔性路面道路的主要设计参数

2.2有限元模型

2.2.1模型建立

根据表1所示道路结构参数，采用ABAQUS/Standard模块建立有限元模型，面层的沥青混合料采用Burgers模型。在建立模型时，考虑到无法将模型尺寸取为无限大，在保证计算精度的同时，为避免增加过多的计算工作量，根据计算经验和文献［15]中的数据，将模型尺寸定为10 m×8 m×6 m，即水平方向长10 m、宽8 m，深度方向为6 m。

假定各结构层为均匀、连续、各向同性的粘弹性体，基础的四周均为完全约束，基础底面的位移为零（如图4所示）。采用双轮荷载，双轮中心间距为32 cm。对模型进行网格划分时，考虑到计算精度及工作量要求，面层选取的网格单元为0.1 m，在荷载作用区域内进行网格加密，远处网格逐渐变疏，基层网格单元为0.2 m，底基层和土基网格单元为0.3 m，网格划分后的路面模型如图5所示，其中Y轴为竖向坐标，Z轴为行车方向。采用三维六面体八节点线性减缩积分等参单元（C3D8R）求解，网格如果存在扭曲变形，也不会对计算精度产生太大的影响，同时能避免在弯曲荷载作用下发生剪切自锁。

图4　道路有限元模型示意图

图5　网格划分结果示意图

2.2.2移动荷载的施加

测试车辆采用东风JN150型标准车，前后轴分别为6.8、17.4 k N，车速取0、20、40、60 km/h。

在车辆前进方向上设置荷载移动带，以此模拟车辆的移动。行车距离取移动带沿路面水平向的长度，表面上所施加的均布荷载宽度即为路面横向宽度，将车轮加载长度均分成3个小矩形，以小矩形的宽度划分整个荷载移动带，车辆荷载在初始状态下占据前3个小矩形（如图6所示）。

图6　移动荷载施加示意图

在移动荷载施加过程中，借助ABAQUS软件中的用户子程序平台，使用Fortran语音编写程序编写子程序施加移动荷载，以此模拟车辆荷载沿移动带向前移动的过程。

2.3模型验证

经过数值模拟计算，得到应力云图，图7为汽车后轴荷载17.4 k N、车速20 km/h时的应力云图。

图7　移动荷载作用下的应力云图（单位：Pa）

从图7可看出：在汽车后轴荷载为17.4 k N、速度为20 km/h的车辆荷载作用下，该道路最大应力值为0.005 753 MPa，模型选取的尺寸已超过荷载的影响范围，其结果准确、可信。

文献［15]中的实测值为车轮下距路面顶面60 cm处的应力值，模拟计算结果如图8所示，最大应力值为0.005 462 MPa。

图8　深度60 cm处的应力云图（单位：Pa）

通过数值模拟计算得到该柔性路面道路在速度分别为0、20、40、60 km/h时的应力值，与文献［15]中工程算例结果的对比如表2和图9所示。

从表2及图9可看出：在移动荷载作用下，实测应力值始终略小于数值模拟计算值，车速变化对路面结构的应力有影响，总体来说呈现随速度增大而应力减小的趋势；实测应力值与数值模拟计算值的误差小于10％，在允许误差范围内，说明所建立的有限元模型合理。

表2　柔性路面道路应力实测值及数值模拟结果

图9　柔性路面道路实测值及数值模拟结果对比

3　柔性路面道路刚度分析

3.1速度对柔性路面道路刚度的影响

车辆荷载采用标准轴载BZZ-100，轮压为0.7 MPa，车速分别取10、15、20、25和30 m/s，分析速度变化对移动荷载作用下柔性路面道路刚度的影响。计算点位于路面结构车轮荷载正下方中心。移动荷载作用下柔性路面道路刚度值按式（2）计算，计算结果如表3、图10、图11所示。

式中：P为每个轮胎所承受的荷载；Y为柔性路面道路面层的最大竖向位移。

表3　不同速度下的数值模拟结果

由表3及图10可知：在移动荷载作用下，车辆速度的变化会对柔性路面面层的最大竖向位移产生明显影响，随着速度的增大，面层最大竖向位移先减小后增大。当车辆速度从10 m/s增加到20 m/s 时，面层最大竖向位移值不断减小；而当速度从20 m/s增加到30 m/s时，面层最大竖向位移值不断增大。位移波动范围在10％以内。

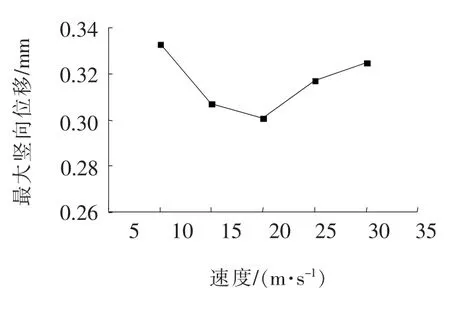
图10　不同速度下面层最大竖向位移曲线

图11　不同速度下柔性路面道路刚度曲线

由图11可看出：在移动荷载作用下，柔性路面道路刚度随速度变化的规律与面层最大竖向位移相反，随着车速的增大，道路刚度呈现先增大后减小的趋势。当速度从10 m/s增加到20 m/s时，道路刚度增大，增幅为8.47％和1.99％；当速度从20 m/s增加到30 m/s时，道路刚度减小，减幅为5.15％和2.46％；道路刚度最大值为8.305 6×104N/mm，最小值为7.507 5×104N/mm，变化幅度在10％以内。说明在15～25 m/s范围内可找到一个临界速度，当荷载的移动速度小于该临界速度时，道路刚度呈现增大趋势；当荷载的移动速度大于该临界速度时，道路刚度呈现减小趋势。

该文采用沥青混合料的Burgers模型，考虑面层材料的粘弹性，在车辆荷载不变的情况下车辆速度增大，面层材料的粘弹性阻尼力增大，面层最大竖向位移减小，道路刚度增大。速度继续增大，因粘弹性作用效应改变，面层最大竖向位移增大，道路刚度减小，有趋于稳定的趋势。

3.2车辆载重对柔性路面道路刚度的影响

目前，汽车超载已普遍，有必要对不同车辆载重作用下柔性路面道路刚度进行研究。取车速为20m/s，车辆后轴载重分别为100、200、300、400、500 k N，分析车辆载重对柔性路面道路刚度的影响。计算结果如表4、图12、图13所示。

表4　不同车辆载重作用下数值模拟结果

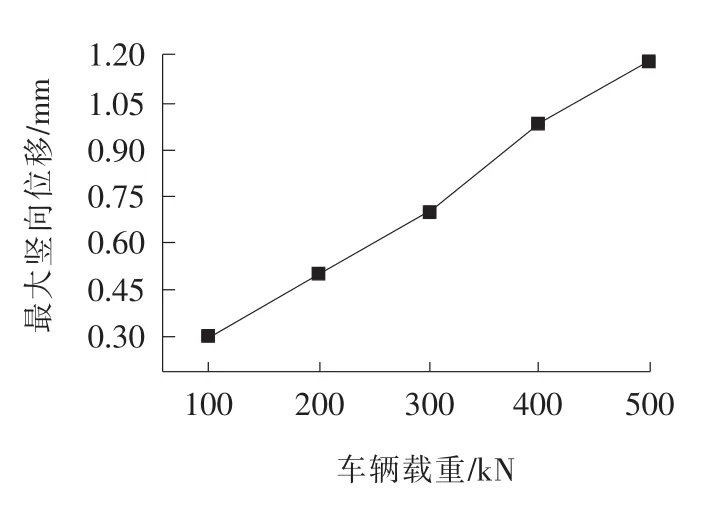
图12　不同载重下面层最大竖向位移曲线

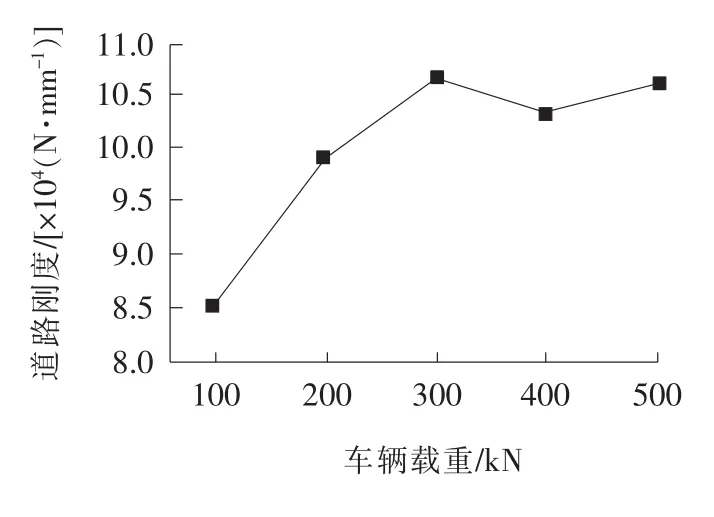
图13　不同载重下柔性路面道路刚度曲线

由表4和图12可以看出：路面最大竖向位移随着车辆载重的增加而增大，并且增加幅值很大，载重从100 k N开始以100 k N的间隔增大到500 k N 时，路面最大竖向位移增大幅值分别为72.35％、39.41％、37.36％和21.72％。说明随着车辆载重的增加，路面最大竖向位移会一直增加直至超负荷，从而引起路面破坏。

从图13可以看出：道路刚度随载重的变化规律不同于路面最大竖向位移的变化规律。在一定载重范围内，随着车辆载重的增加，道路刚度总体呈增大趋势，但因为考虑面层材料的粘弹性，道路刚度变化呈非线性关系。说明车辆载重对柔性路面道路刚度的影响较大。

3.3温度对柔性路面道路刚度的影响

因为沥青混合料的力学特性，柔性路面结构受温度影响最严重，故有必要对不同温度下柔性路面道路的刚度进行分析。取载重为300 k N，速度为20 m/s，温度分别为15、20、25℃进行分析，结果如表5、图14、图15所示。

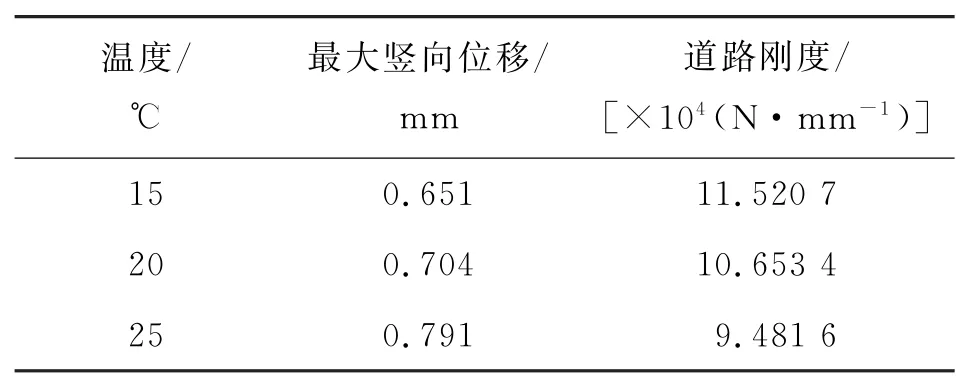
表5　不同温度下数值模拟结果

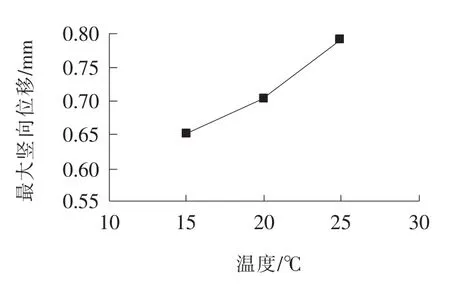
图14　不同温度下面层最大竖向位移曲线

图15　不同温度下柔性路面道路刚度曲线

由表5、图14、图15可看出：随着温度的升高，面层最大竖向位移增大，道路刚度减小。温度为15℃时，道路刚度最大，为11.520 7×104N/mm；温度为25℃时，道路刚度最小，为9.481 6×104N/mm。分析其原因，温度越高，面层沥青混合料的粘弹性阻尼力减小，弹性模量减小，导致道路刚度减小，表现在宏观上为路面面层竖向位移增大。

3.4材料模量变化对柔性路面道路刚度的影响

由于路面结构是分层铺筑的，各结构层的材料模量变化会影响到路面结构的响应。针对柔性路面道路刚度问题，根据JTG D50-2006《公路沥青路面设计规范》，改变柔性路面结构各层的材料模量，采用正交试验设计方法，运用极差方法分析材料模量变化对移动荷载作用下柔性路面道路刚度的影响。

为了减少计算量，参考前述有限元模型，将上面层、中面层和下面层合并为一层即面层，采用中粒式密级配沥青砼（AC-20Ⅰ），建立4层柔性路面道路模型。将柔性路面最大竖向位移和道路刚度作为试验考核指标，确定A面层模量、B基层模量、C底基层模量、D土基模量共4个因素，每个因素3个水平，采用L9（34）正交表，试验因素水平如表6所示，试验设计计算方案及计算结果如表7、表8所示。

表6　正交试验因素水平MPa

表7　正交试验设计计算方案

采用极差分析方法对柔性路面道路刚度有较大影响的因素进行检查和分析，找出影响显著的因素。极差越大，则该因素对试验考核指标的影响越显著。极差分析结果如表9所示。各因素水平与柔性路面道路刚度的关系如图16所示。

由表9可知：以最大竖向位移和道路刚度为考核指标时，4个因素影响程度排序为土基模量>底基层模量>基层模量>面层模量，在移动荷载作用下，柔性路面道路刚度随着各结构层材料模量的增大而增大，土基模量对道路刚度的影响最为显著。

表8　正交试验结果

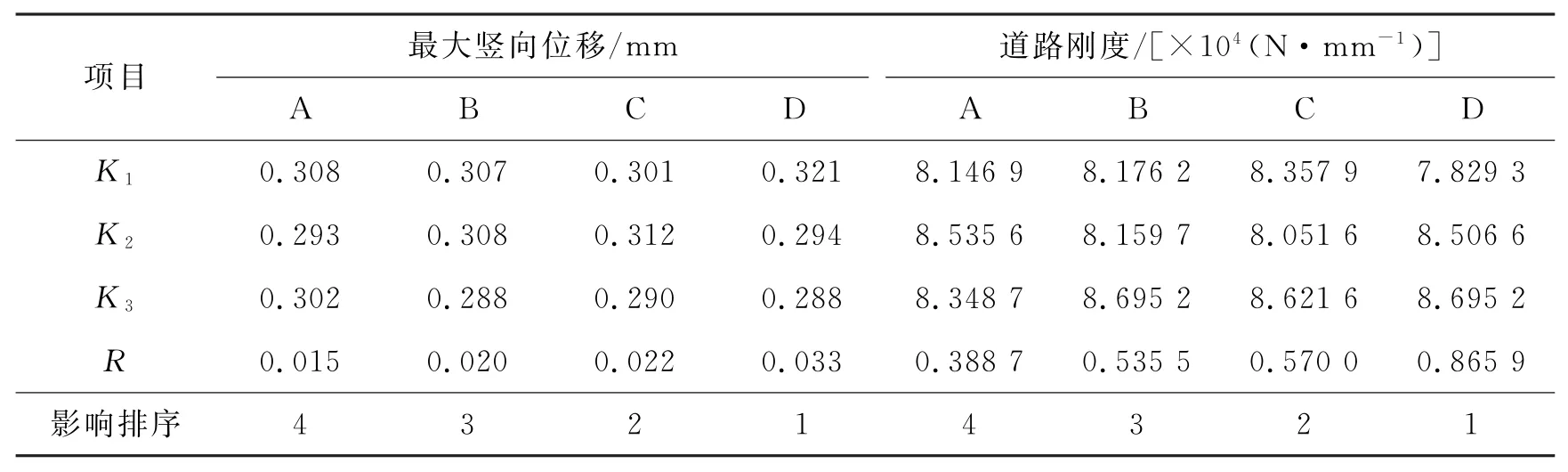
表9　极差分析结果

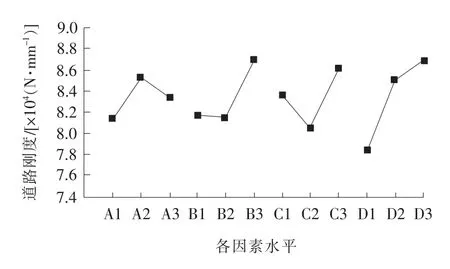
图16　各因素与道路刚度的关系

根据平均值Ki，可在一定范围内确定柔性路面各结构层材料模量的最优组合：每组试验结果中道路刚度最大值点对应的模量值即构成最优组合。如图16所示，A2、B3、C3、D3为最优组合，即当面层模量为1 600 MPa、基层模量为1 500 MPa、底基层模量为800 MPa、土层模量为50 MPa时，柔性路面道路的刚度最大。

4　结论

该文参照现有弹性层状体系模型，依据层状粘弹性理论体系，建立了柔性路面道路层状粘弹性体系力学模型；借助ABAQUS有限元软件，考虑面层粘弹性特性，建立了移动荷载作用下柔性路面道路三维有限元模型，并编写子程序实现移动荷载的施加。采用文献［15]中的工程实例，通过ABAQUS/Standard计算模块，分析了移动荷载作用下柔性路面的最大竖向压应力，将计算结果与工程实例进行比较，数值模拟计算值与实测值接近，最大误差为6.25％，三维有限元模型合理、准确。

车速、车辆荷载、温度和材料模量变化对移动荷载作用下柔性路面道路刚度有明显影响。面层材料的粘弹性作用，使得存在一个临界速度，随着车速的增大，柔性路面道路刚度呈现增大趋势，当车速继续增大超过临界速度时，柔性路面道路刚度呈现减小趋势；在一定的车辆载重范围内，随着车辆载重的增加，道路刚度总体呈增大趋势；温度越高，道路刚度越小；随着各结构层材料模量的增大，柔性路面道路刚度增大，其中土基模量对柔性路面道路刚度的影响最显著。

［1］秦建平.道路工程［M].武汉：武汉理工大学出版社， 2010.

［2］邓学钧，孙璐.车辆-地面结构系统动力学［M].北京：人民交通出版社，2000.

［3］刘振旺.某装甲车辆车内隔振降噪特性研究［D].太原：中北大学，2008.

［4］Blab R，Harvey J T.Modeling measured 3D tire contact stresses in a viscoelasticfe pavement model［J].The International Journal of Geomechanics，2002，2（3）.

［5］Acum W E A，Fox L.Computation of load stresses in a three-layer slastic system［J].Geotechnique，1951，2 （4）.

［6］郭文复.多层半无限弹性体在圆形荷载作用下的解析解［J].力学学报，1984，16（3）.

［7］郭大智.刚性承载板下弹性多层连续体应力和位移分析［J].哈尔滨建筑大学学报，1995，28（2）.

［8］孟凡顺.多层半无限弹性体在任意荷载作用下的解析解［J].工程力学，1997，14（3）.

［9］时永澄，吴淇泰.一个动力接触问题的数值解［J].力学学报，1985，17（4）.

［10］王凯.N层弹性连续体系在圆形均布垂直荷载作用下的力学计算［J].土木工程学报，1982，15（2）.

［11］任瑞波，钟阳，殷建华.路面结构在动荷载作用下路表弯沉的求解［J].岩土工程学报，2000，22（6）.

［12］郭大智，冯德成.层状弹性体系力学［M].哈尔滨：哈尔滨工业大学出版社，2001.

［13］Brown S F.An introduction to the analytical design of bituminous pavement［R].The Department of Civil Engineering，University of Nottingham，1980.

［14］龙晓日韦.现代道路路基路面工程［M].北京：清华大学出版社，2004.

［15］胡安宇，林旻，张洪亮.移动车辆荷载作用下路基中压应力测试［J].建设机械技术与管理，2008（10）.

［16］王金昌，陈页开.ABAQUS在土木工程中的应用［M].杭州：浙江大学出版社，2006.

［17］张文元.ABAQUS动力学有限元分析指南［M].北京：中国图书出版社，2005.

［18］高允彦.正交及回归试验设计方法［M].北京：冶金工业出版社，1988.

［19］宋一凡，陈榕峰.基于路面不平整度的车辆振动响应分析方法［J].交通运输工程学报，2007，7（4）.

［20］张洪亮，胡长顺，许伟清.移动荷载作用下柔性路面的动力响应［J].长安大学学报：自然科学版，2005，25 （5）.

［21］杨果岳.车辆随机荷载与柔性路面相互作用的研究［D].长沙：中南大学，2007.

［22］王峰；移动荷载作用下过湿地段路基路面动力响应有限元分析［D].西安：长安大学，2009.

U412.6

A

1671-2668（2016）01-0078-07

2015-09-08

国防重大基础研究资助项目（613153）