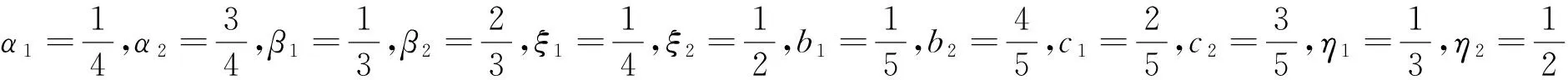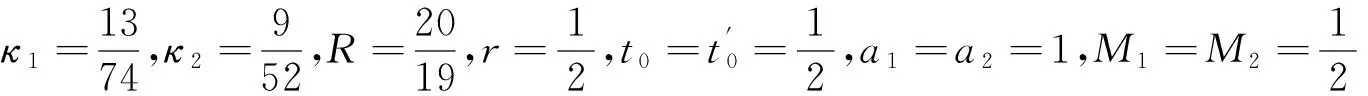一类多点共振方程组边值问题正解的存在性
江卫华,杨彩霞
(河北科技大学理学院,河北石家庄 050018)
一类多点共振方程组边值问题正解的存在性
江卫华,杨彩霞
(河北科技大学理学院,河北石家庄050018)
求解共振微分方程边值问题解的存在性比较困难,要得到共振微分方程边值问题的正解更加困难。针对研究领域中这一问题,着重研究了一类多点共振微分方程组边值问题正解的存在性。在前人研究成果的基础上,选取的不同的算子,将方程扩展为方程组。通过在合适的空间中定义恰当的范数使之成为Bananch空间,利用O'Regan和Zima所研究出来的范数形式的Leggett-Williams定理,对非线性项做出合理的假设条件,得到了共振微分方程组边值问题正解的存在性定理。
常微分方程其他学科;边值问题;共振;正解;方程组
本文研究多点共振微分方程组边值问题:
(1)
正解的存在性。

对边值问题解和正解的研究已经取得了大量的研究成果[1-6]。特别是共振边值问题一直以来受到广泛关注,并且已经取得了很多成果[7-14]。文献[14]利用范数形式的Leggett-Williams定理给出了如下共振多点边值问题:
(2)
受上述文献启发,本文研究多点共振微分方程组边值问题(1)正解的存在性。
1 预备知识
本文所使用的一些预备知识如下,详细可参见文献[14]。
设X,Y是Banach空间,L:domL⊂X→Y为指数为零的Fredholm算子,即ImL是闭集且dimKerL=codimImL<∞。此时存在连续投影算子P:X→X,Q:Y→Y使得ImP=KerL,KerQ=ImL。又dimImQ=codimImL,因此存在同构J:ImQ→KerL,若限制L在KerP∩domL上,记为LP,则它的逆算子存在,记为KP:ImL→KerP∩domL。方程Lx=Nx等价于x=(P+JQN)x+KP(1-Q)Nx。
引理1[14]设C为X中一个锥,则对每个u∈C{θ},存在一个正数σ(u)使得‖x+u‖≥σ(u)‖x‖,对∀x∈C。
令γ:X→C为保核收缩,即γ为一连续映射,且γx=x,x∈C。并记Ψ:=P+JQN+KP(I-Q)N和Ψγ:=Ψ∘γ。
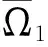
1°在X的任意有界子集上,QN:X→Y连续有界,KP(I-Q)N:X→X是紧的;
2°对任何x∈∂Ω2∩domL,λ∈(0,1),Lx≠λNx;
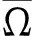
4°dB([I-(P+JQN)γ]|Ker L,KerL∩Ω2,0)≠0,其中dB代表Brouwer度;
5°存在u0∈C{0}使得当x∈C(u0)∩∂Ω1,有‖x‖≤σ(u0)‖Ψx‖成立,其中C(u0)={x∈C:μu0⪯x},μ为某些大于0的数,并且σ(u0)满足对∀x∈C不等式‖x+u0‖≥σ(u0)‖x‖都成立;
6° (P+JQN)γ(∂Ω2)⊂C;
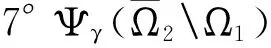
2 主要结论
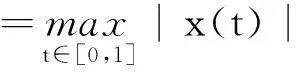
定义算子L:domL⊂X→Y,L(u,v)=(L1u,L2v)=(-u″(t),-v″(t)),t∈[0,1],
其中,
domL=domL1×domL2,
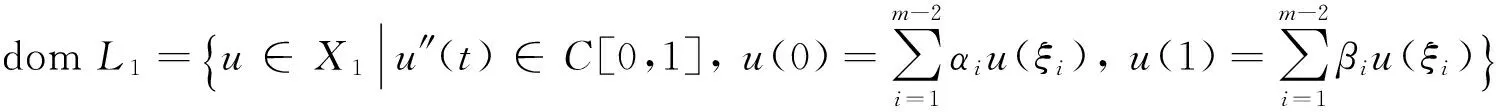

定义N:X→Y为N(u,v)=(N1(u,v),N2(u,v)),其中N1(u,v)=f(t,u(t),v(t)),N2(u,v)=g(t,u(t),v(t)),t∈[0,1]。那么边值问题(1)等价于L(u,v)=N(u,v)。显然,KerL={(u,v)∈domL:(u(t),v(t))=(c1,c2),t∈[0,1],c1,c2∈R}。
定义函数G(s),H(s),s∈[0,1]:
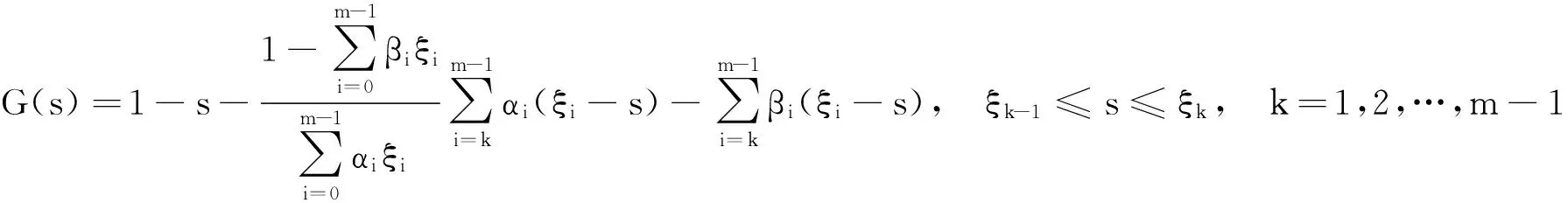
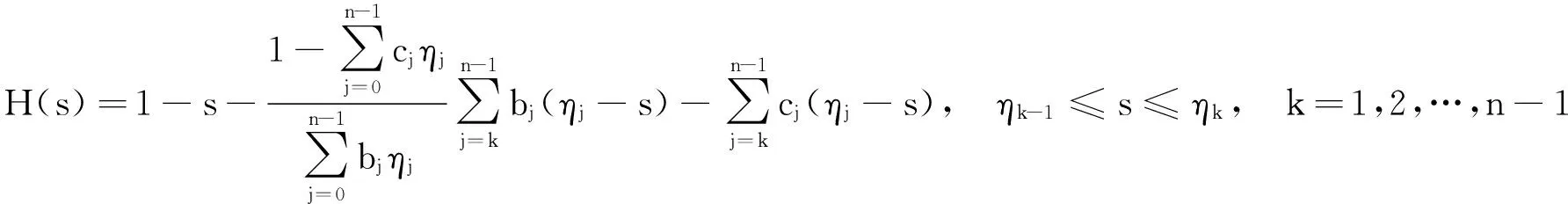
显然,0≤G(s)≤1,0≤H(s)≤1,s∈[0,1]。
定义函数U1(t,s),U2(t,s)如下:
定义正数:
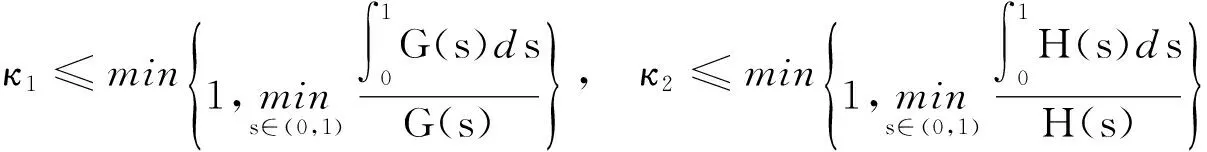
定理2连续函数f:[0,1]×R×R→R与g:[0,1]×R×R→R满足以下条件。
假设存在R∈(0,+∞),使得
H1)f(t,u,v)>-κ1u,g(t,u,v)>-κ2v,f(t,u,v)U1(t,s)≥-u,g(t,u,v)U2(t,s)≥-v,其中(u,v)∈[0,R]×[0,R],t,s∈[0,1]。
H2)f(t,R,v(t))<0,t∈[0,1],0≤v(t)≤R,v(t)∈C[0,1],g(t,u(t),R)<0,t∈[0,1],0≤u(t)≤R,u(t)∈C[0,1]。
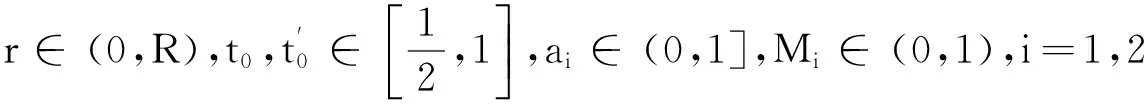

则共振边值问题(1)至少有1组正解。
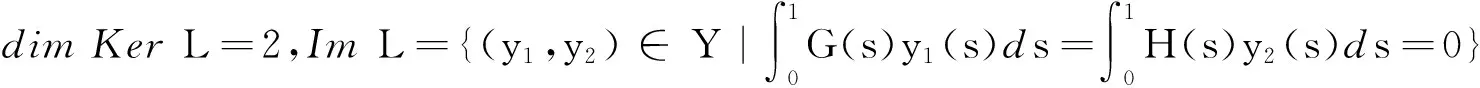

(3)
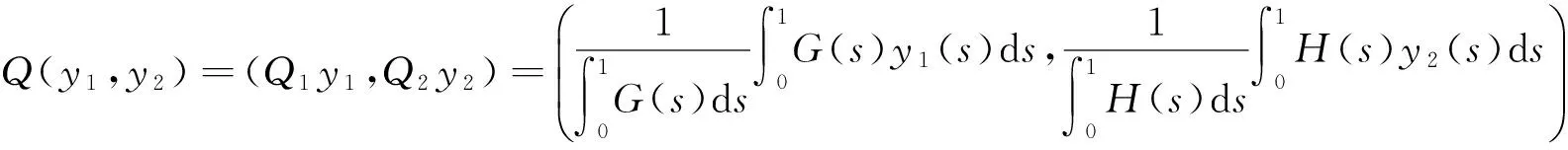
(4)
显然有ImP=KerL,P2(u,v)=P(u,v)且X=KerP⊕KerL。
由式(4)知:
Q2(y1,y2)=Q(y1,y2)且Y=ImL⊕ImQ,
dimImQ=dimKerL即dimKerL=codimImL。
故L是指数为0的Fredholm算子。
接下来将证明L|dom L∩Ker P的逆KP,KP:ImL→domL∩KerP,
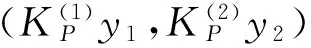
其中:
通过计算有,LPKP=I。因此,LP的逆算子是KP。
定义锥C和有界集Ω1,Ω2如下:
C={(u,v)∈X:u(t)≥0,v(t)≥0,t∈[0,1]},
Ω1={(u,v)∈X:M1‖u‖<|u(t)| Ω2={(u,v)∈X:‖u‖ 因此有: ‖QN(u,v)‖=max{‖Q1N1(u,v)‖,‖Q2N2(u,v)‖}= 所以QN:X→Y有界。又QN:X→Y连续,故QN:X→Y连续有界。 综上分析有KP(I-Q)N:X→X是紧的。这说明定理1的条件1°成立。 假设存在(u0,v0)∈C∩∂Ω2∩domL及λ0∈(0,1)使得L(u0,v0)=λ0N(u0,v0),即 u″0(t)+λ0f(t,u0(t),v0(t))=0,v″0(t)+λ0g(t,u0(t),v0(t))=0,t∈[0,1]。 设存在t1,t2∈[0,1]使得u0(t1)=R或者v0(t2)=R。 如果u0(t1)=R,有0≥u″0(t1)=-λ0f(t1,u0(t1),v0(t1))=-λ0f(t,R,v0(t1))。 如果v0(t2)=R,有0≥v″0(t2)=-λ0g(t2,u0(t2),v0(t2))=-λ0g(t2,u0(t2),R) 与条件H2)矛盾。所以条件2°成立。 定义Hλ:KerL∩Ω2→R,λ∈[0,1]如下: Hλ(c1,c2)=(I-λ(P+JQN)γ)(c1,c2):= (H1(c1,c2,λ),H2(c1,c2,λ))= 其中:ci∈[-R,R];λ∈[0,1]。 假设H1(c1,c2,λ)=0,H2(c1,c2,λ)=0。由条件H1)有: 因此H1(c1,c2,λ)=0意味着c1≥0以及H2(c1,c2,λ)=0意味着c2≥0。此外,有H1(R,c2,λ)≠0,或者H2(c1,R,λ)≠0。 事实上, 这与条件H2)矛盾。对(c1,c2)∈∂Ω2∩KerL,λ∈[0,1]有Hλ(c1,c2)≠(0,0), 因此,有: dB([I-(P+JQN)γ]Ker L,KerL∩Ω2,0)= dB(H1(c1,c2),KerL∩Ω2,0)= dB(H1(c1,c2),KerL∩Ω2,0)= dB(I,KerL∩Ω2,0)= 1≠0。 因此4°成立。 设 其中: 对(u,v)∈∂Ω2,有: 由于 所以,有(P+JQN)γ(∂Ω2)⊂C。因此定理1中的条件6°,7°成立。 取(u(t0),v(t0))≡(1,1),t∈[0,1]和σ(u0,v0)=1,有 (u0,v0)∈C{0,0}, C(u0,v0)={(u,v)∈C:u(t)>0,v(t)>0,t∈[0,1]}。 设(u,v)∈C(u0,v0)∩∂Ω1,有M1‖u‖≤u(t)≤r,M2‖v‖≤v(t)≤r,t∈[0,1]。 对(u,v)∈C(u0,v0)∩∂Ω1,如果‖u‖=r有 M1‖u‖+(1-M1)‖u‖=‖u‖。 因此,有‖Ψ(u,v)‖=max{|Ψ1(u,v),Ψ2(u,v)|}≥max{‖u‖,‖v‖}=‖(u,v)‖。所以对所有(u,v)∈C(u0,v0)∩∂Ω1,有‖(u,v)‖≤σ(u0,v0)‖Ψ(u,v)‖。定理1的条件5°成立。 考虑如下共振边值问题: (5) 且 2)f(t,R,v(t))<0,t∈[0,1],0≤v(t)≤R,v(t)∈C[0,1], g(t,u(t),R)<0,t∈[0,1],0≤u(t)≤R,u(t)∈C[0,1] 。 因此满足定理2的所有条件。因此共振问题(5)至少有1组正解。 / [1]MA R, WANG H. Positive solutions of nonlinear three-point boundary-value problems[J]. Electronic Journal of Differential Equations, 2003,279(1):216-227. [2]YANG Liu, LIU Xiping, JIA Mei. Multiplicity results for second-orderm-point boundary value problem [J]. Journal of Mathematical Analysis and Applications, 2006,324(1):532-542. [3]HAN Xiaoling. Positive solutions for a three-point boundary value problem[J]. Nonlinear Analysis, 2007,336(3):556-568. [4]MA Ruyun. Multiplicity results for a three-point boundary value problem at resonance[J]. Nonlinear Analysis, 2003,53(6):777-789. [5]HENDERSON J. Double solutions of three-point boundary-value problems for second-order differential equations [J].Electronic Journal of Differential Equations, 2004,136(2): 281-286. [6]ZHANG G,SUN J. Positive solutions ofm-point boundary value problems[J]. Journal of Mathematical Analysis and Applications, 2004,291(2):406-418. [7]索秀云,江卫华,陆静.二阶多点共振边值问题的正解[J].数学的实践与认识,2011,41(15):247-253. SUO Xiuyun, JIANG Weihua,LU Jing.Positive solution for seeond order multipoint boundary value problem at resonance[J].Mathematics in Practice and Theory,2011,41(15):247-253. [8]ZHAO Y, SUN S, HAN Z. Positive solutions for boundary value problems of nonlinear fractional differential equations[J]. Computers & Mathematics with Applications, 2011, 217: 6950-6958. [9]MA Ruyun.Existence results of am-point boundary value problem at resonance[J]. Journal of Mathematical Analysis and Applications, 2004, 294(1): 147-157. [10]GE W, REN J. An extension of Mawhin’s continuation theorem and its application to boundary value problems withp-laplacian[J]. Nonlinear Analysis Theory Methods and Applications,2004, 58(3/4): 477-488. [11]PHUNGA P D, TRUONG L X. On the existence of a three point boundary value problem at resonance inRnRn[J]. Journal of Mathematical Analysis and Applications, 2014, 416(2): 522-533. [12]SU X. Positive solutions to singular boundary value problems for functional differential equations with changing sign nonlinearity[J]. Computers & Mathematics with Applications, 2012,64(10): 3425-3435. [13]JIANG Weihua, QIU Jiqing. Solvability of (k,n-k) conjugate boundary-value problems at resonance[J].Electronic Journal of Differential Equations, 2012,19(3):2088-2090. [14]INFANTE G, ZIMA M. Positive solutions of multi-point boundary value problems at resonance[J]. Nonlinear Analysis,2013,69(8):2458-2465. Existenceofpositivesolutionsformulti-pointresonancesystemsofdifferentialequationswithboundaryvalueconditions JIANGWeihua,YANGCaixia (SchoolofScience,HebeiUniversityofScienceandTechnology,Shijiazhuang,Hebei050018,China) Itisdifficulttostudytheexistenceofsolutionsforboundaryvalueproblemsofdifferentialequationsatresonance,moreover,togetpositivesolutionsofboundaryvalueproblemsfordifferentialequationsatresonanceismoredifficult.Toresearchthisproblem,theexistenceofpositivesolutionsforacoupleofdifferentequationswithmulti-pointboundaryvalueconditionsatresonanceisstudied.Onthebasisofpreviousresearches,choosingadifferentoperator,theequationisextendedtoacoupleofdifferentequations.BydefiningthecorrectnormintheproductspaceswhichbecomeBanachspaces,andusingtheLeggett-Williamsnorm-typetheoremduetoO'ReganandZima,thenonlineartermsatisfiesreasonableassumptions,andtheexistenceofpositivesolutionsforacoupledofdifferentequationswithmulti-pointboundaryvalueconditionsatresonanceisobtained. otherdisciplinesofordinarydifferentialequation;boundaryvalueproblem;resonance;positivesolution;differentialequation 1008-1542(2016)04-0340-09 10.7535/hbkd.2016yx04005 2016-01-26; 2016-04-26;责任编辑:张军 国家自然科学基金(11171088);河北省自然科学基金(A2013208108) 江卫华(1964—),女,河北邯郸人,教授,博士,主要从事应用泛函分析、常微分方程边值问题方面的研究。 E-mail:jiangweihua64@163.com O175MSC(2010)主题分类:34B18 A 江卫华,杨彩霞.一类多点共振方程组边值问题正解的存在性[J].河北科技大学学报,2016,37(4):340-348. JIANGWeihua,YANGCaixia.Existenceofpositivesolutionsformulti-pointresonancesystemsofdifferentialequationswithboundaryvalueconditions[J].JournalofHebeiUniversityofScienceandTechnology,2016,37(4):340-348.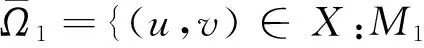


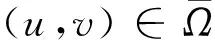


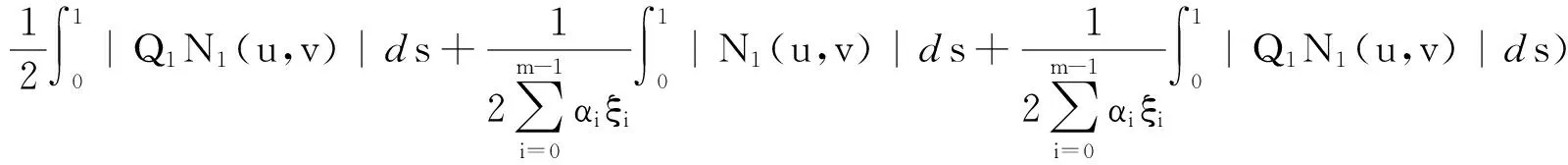
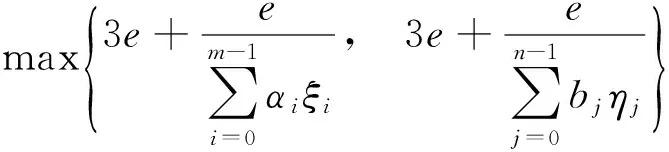
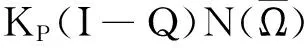

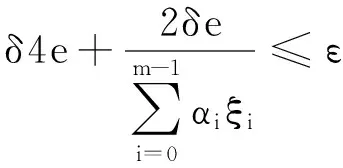

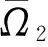
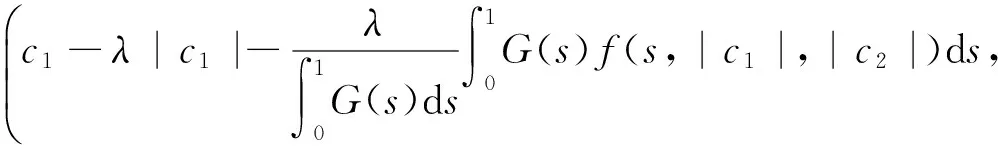
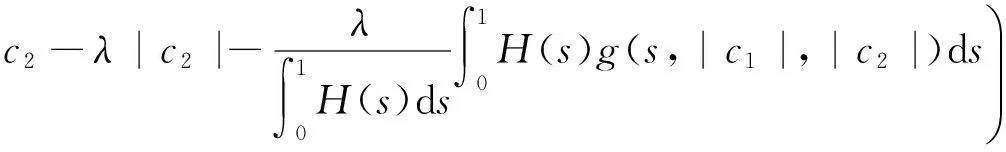



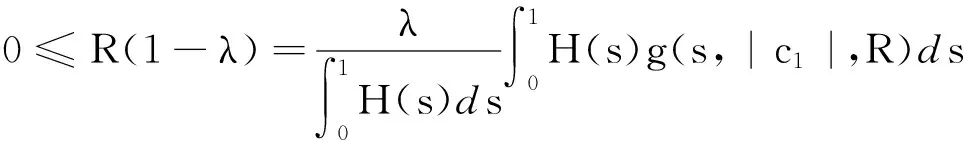
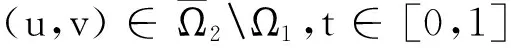

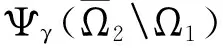
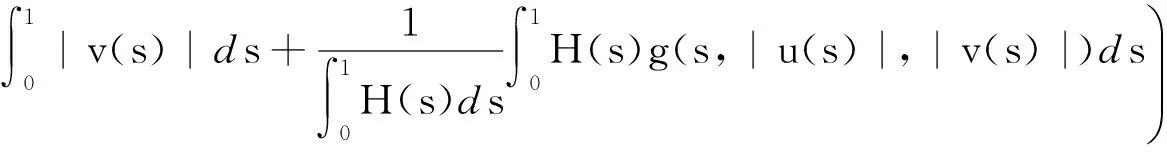



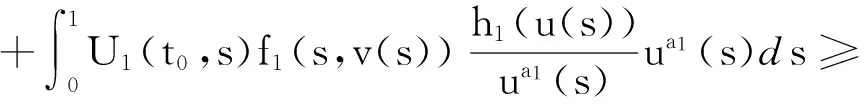
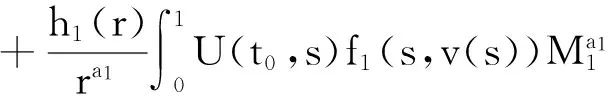
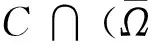
3 例 子