基于距离差、能量比和到达角的两麦克风声源定位

窦育强，王晖，张勤

(1中国传媒大学 信息工程学院 北京 100024；2河南师范大学 计算机与信息工程学院 河南新乡 453007)



基于距离差、能量比和到达角的两麦克风声源定位

窦育强1，2，王晖1，张勤1

(1中国传媒大学 信息工程学院 北京 100024；2河南师范大学 计算机与信息工程学院 河南新乡 453007)

减少定位声源所需麦克风数量对于特定场合是重要的，提出在两麦克风条件下利用距离差、能量比和到达角联合对单个声源进行二维定位的最大似然法和一种闭式解。在高斯噪声条件下，最大似然法将转化为加权最小二乘问题，为减小求解复杂度利用了粒子群算法进行迭代求解。通过仿真分析了最大似然法和闭式解法的抗噪声性能。

距离差；能量比；到达角；最大似然；粒子群

1　引言

近年来，基于麦克风阵列的声源定位得到了很多研究者的关注。一类常用的方法是基于距离差的方法[1-4]，已经得到了很多研究；另一类基于能量和能量比的定位方法也受到了重视。基于能量比的方法首先由Hu和Li[5]提出，文中给出了基于能量的最大似然估计方法，在对单个声源定位时给出了基于能量比的最小二乘法。D.Blatt和A.D.Hero[6]针对最小二乘算法容易陷入局部最优的缺点，提出了一种凸集投影法，在一定条件下可求得全局最优解。2007年，K.C.Ho和Ming Sun[7]提出了一种利用能量比信息进行定位的代数闭式解。Chen Feng等[8]利用阵列接收信号的能量信息建立了实现多源定位的压缩感知模型。这些方法都仅仅利用了声源的能量比特征，并且所用麦克风阵列阵元数量都超过两个。W.Cui[9]和Pourmohammad[10]利用距离差和能量比对声源在二维空间进行定位，给出了闭式解，并且将麦克风数量降到了两个，但信噪比过高时，可能存在无解情况，还需要对得到的两根做分析。Wenyi Zhang[11]利用两个麦克风实现了对多声源的方向估计。本文对利用两麦克风进行声源定位方法进行了分析，给出了基于距离差、能量比和到达角联合进行声源定位的最大似然方法，并利用粒子群算法进行求解；给出了利用距离差、能量比和到达角联合进行声源定位的闭式解。

本文第二部分论述了利用距离差、能量比和到达角联合进行声源定位的方法原理，第三部分对所提算法进行了实验仿真，并对结果进行了分析，第四部分得出结论。

2　二维声源定位原理

2.1基于距离差、能量比和到达角的最大似然法

在笛卡尔坐标系中，两个麦克风坐标分别为r1=(x1，y1)和r2=(x2，y2)，声源位于r=(x，y)点处，则声源到两个麦克风的距离分别为：

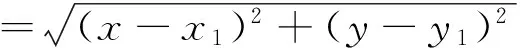
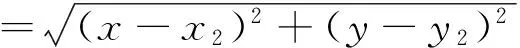
声源信号为x(t)，幅度衰减与距离成反比，在第i个麦克风处接收到信号为

其中gi为第i个麦克风增益，ξi为观测噪声，首先忽略噪声，有

假设所有麦克风增益均为1，忽略相位延迟引起的能量差，则麦克风1与麦克风2接收到的信号能量比为

κ12称为能量比因子，则

(1)

声源距离麦克风2和麦克风1的距离差为

d12=cτ12=‖r2‖-‖r1‖

(2)

τ12为声源到麦克风2与麦克风1的时延差τ12=τ2-τ1，c为声速。

由于实际测量会有误差存在，实际的能量比和距离差估计值应该表示为

(3)

其中

f2(r)=‖r2‖-‖r1‖

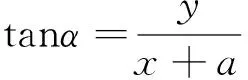
(4)

由于测量误差的存在，实际的到达角余弦应该表示为

(5)

其中

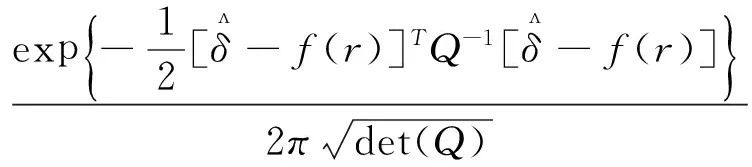
(6)

vi，j(t+1)=ωvi，j(t)+c1s1[pi，j-ui，j(t)]

+c2s2[pg，j-ui，j(t)]

ui，j(t+1)=ui，j(t)+vi，j(t+1)，j=1，2.，

其中c1和c2为学习因子，均大于零，ω为惯性权重，s1和s2为随机数，在0到1之间均匀分布。

2.2基于距离差、能量比和到达角的闭式解

整理(1)式与(2)式得

(7)

(8)

将(7)式和(8)式整理可以得到两个用于定位的圆

其中

再整理可以得到关于x，y，R2=x2+y2的两个线性方程

(9)

(10)

其中

将(3)式也写成关于x，y，R2的线性方程

kx-y+0·R2=-ak

(11)

其中k=tanα。

将式(9)，(10)和 (11)写成矩阵形式

对其进行求解得

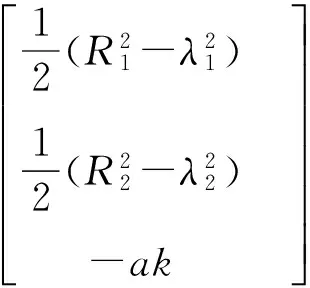
3　仿真与分析

为了检验本文算法的性能，进行了计算机仿真实验。为方便论述，分别记2.1和2.2中的算法为方法1和方法2；记文献[9]中的算法为方法3。

两个麦克风位置分别为r1=(-40，0)和r2=(40，0)，声源位于r=(1346，2350)，单位均为cm。

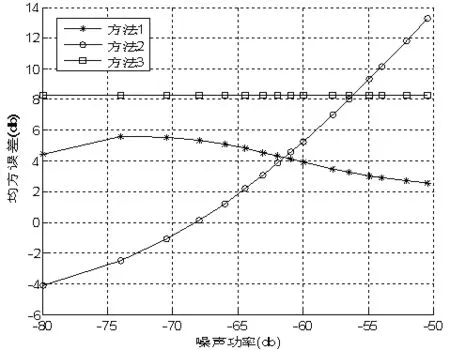
图1　方法1，方法2和方法3的定位均方误差比较，　

图2　方法1，方法2和方法3的定位均方误差比较，　

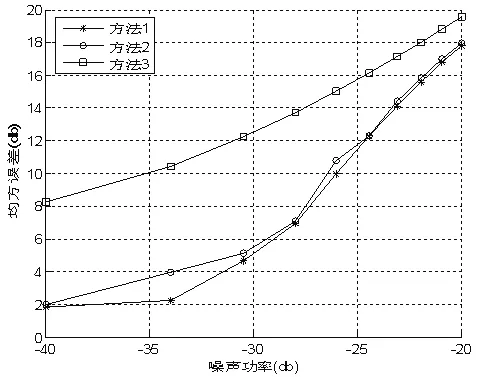
图3　方法1，方法2和方法3的定位均方误差比较，　

4结论

本文对基于两个麦克风的声源定位方法进行了研究，提出了利用距离差、能量比和到达角的最大似然解法和一种闭式解法。最大似然法转化为加权最小二乘问题后，利用粒子群算法进行求解。

通过仿真实验表明，利用最大似然法具有优于其他算法的性能，闭式解法在高信噪比时具有一定的优越性。

[1]Schau H C，Robinson A Z.Passive source localization employing intersection spherical、surfaces from time-of-arrival differences[J].IEEE Transactions on Acoustic，Speech and Signal Processing，1987，35(8)：1223-1225.

[2]Huang N，Benesty J，Elko G W，et a1.Real-time passive source localization：an unbiased linear-correction least-squares approach[J].IEEE Transactions on Speech and Audio Processing，2001，9(8)：943-956.

[3]K C Ho.bias reduction for an explicit solution of source localization using tdoa[J]. IEEE Trans Signal Process，2012，60(5)：2101-2114.

[4]Jamali-Rad，H，Leus，G.Sparsity-Aware Multi-Source TDOA Localization[J]. in Signal Processing，IEEE Transactions on ，2013，61(19)：4874-4887.

[5]DLiandYHHu.Energybasedcollaborativesourcelocalizationusingacousticmicro-sensorarray[J].EURASIPJApplSignalProcess，2003，4：321-337.

[6]DBlattandADHero.Energy-basedsensornetworksourcelocalizationviaprojectionontoconvexsets[J].IEEETransSignalProcess，2006，54(9)：3614-3619.

[7]KCHoandMingSun.AnAccurateAlgebraicClosed-FormSolutionforEnergy-BasedSourceLocalization[J].IEEETransOnAudioSpeechandLanguageProcessing，2007，15.

[8]ChenFeng，AuWSA，ValaeeS，ZhenhuiTan.Received-Signal-Strength-BasedIndoorPositioningUsingCompressiveSensing[J].inMobile Computing，IEEE Transactions on，2012，11(12)：1983-1993.

[9]WCui，ZCao，andJWei.Dual-microphonesourcelocationmethodin2-Dspace[J].inProcIEEEIntConfAcoust，Speech，SignalProcess，2006，845-848.[10]Pourmohammad A，Ahadi S M.TDE-ILD-based 2D half plane real time high accuracy sound source localization using only two microphones and source counting[J].inElectronicsandInformationEngineering(ICEIE)，2010InternationalConferenceOn，2010，1：566-572.

[11]Wenyi Zhang，Rao B D.A Two Microphone-Based Approach for Source Localization of Multiple Speech Sources[J]. inAudio，Speech，andLanguageProcessing，IEEETransactionson，2010，18(8)：1913-1928.

[12]Kennedy J，Ebethart R.Partiele Swarm Optimization[C].In Proceeding of IEEE International Conference on Neural Networks，Piscataway，NJ：IEEE CS，1995：1942-1948.

[13]Ebethart R，Kennedy J.A new Optimizer using particle swarm theory[C].In：Proceeding of the 6thInternational Symposium on Micro Machine and Human Science，NJ：IEEECS，1995：39-43.

(责任编辑：马玉凤)

Sound Source Localization Using Range Differences，Energy Ratios and Angle of Arrival with Two Microphones

DOU Yu-qiang1，2，WANG Hui1，ZHANG Qin1

(1.Information Engineering School，Communication University of China，Beijing 100024； 2.Computer and Information Engineering School，Henan Normal University，Xinxiang of Henan 453007)

To reduce the required number of microphones of sound source location is important for specific occasions.A maximum-likelihood location estimator and a closed-form estimator are proposed for one sound source localization using range differences of arrival，energy ratios of arrival and angle of arrival with two microphones.The maximum-likelihood method is converted into a weighted least squares problem under the condition of gaussian noise，which is solved by an improved particle swarm optimization (PSO) algorithm.The performance of this algorithms against noise are analyzed in this paper.

range differences；energy ratios；angle of arrival；two microphones；PSO

2016-03-04

国家自然科学基金“三维音频基础理论与关键技术研究”(61231015)

窦育强(1980-)，男(汉族)，河南新乡人，中国传媒大学在读博士，河南师范大学讲师.E-mail：double_story@126.com

TN912

A

1673-4793(2016)03-0026-05