高速斜齿轮设计参数对齿面温度的影响分析

范一龙，付昆昆，霍肇波，于东洋

（中国船舶重工集团公司第七O三研究所，黑龙江哈尔滨150078）

高速斜齿轮设计参数对齿面温度的影响分析

范一龙，付昆昆，霍肇波，于东洋

（中国船舶重工集团公司第七O三研究所，黑龙江哈尔滨150078）

文章中建立了斜齿轮齿面温度有限元分析模型，模型考虑了齿面与空气和润滑油的对流换热，以及齿轮副摩擦产生的热流量.通过与实验测试得到的齿面温度对比来验证该模型.最后，利用该有限元模型分析了典型的齿轮设计参数对齿面温度的影响.结果表明，本文建立的有限元分析模型得到的温度和实验测试结果基本一致，最大误差在5.67%以内；并且，齿面温度随着齿顶高系数和齿宽的增加而增加，并随着螺旋角的增加而上下波动.本文提出的模型为高速斜齿轮抗胶合设计提供了依据.

斜齿轮；齿面温度；有限元；设计参数

0　引言

随着船舶工业的迅猛发展，船用斜齿轮传动正朝着高速重载的方向发展.在啮合过程中齿轮副会产生瞬时的高温，导致轮齿发生较大的热变形，从而增大了减速传动装置的振动与噪声，瞬时温度过高时，甚至啮合齿面会发生胶合失效现象，严重的影响了船用斜齿轮的传动品质.所以，在对斜齿轮基本参数进行设计时，为了比避免胶合失效的发生，需要优化斜齿轮的基本设计参数，并对斜齿轮温度场进行精确的预测.

近年来，国内外学者对轮齿齿面温度的预测做了大量的研究.其中，T.Tobe等[1]以直齿轮在齿宽方向的温度分布为抛物线状作为假设，利用数值法预测了直齿圆柱齿轮的本体温度.K.L.Wang等[2]提出了轮齿瞬时动载荷和齿面温度的计算方法，然后利用有限元方法得到齿轮温度场，并分析分度圆直径、齿顶圆直径以及齿宽对齿面温度的影响.李润方等[3]则是建立了齿轮副热-弹耦合有限元模型，分析变形与接触区法向应力的关系，进而研究载荷、速度及轮齿修形等对齿轮温度场的影响.R.F.Handschuh等[4]提出齿轮啮合产生的热量是由外载荷、滑动速度及摩擦系数确定的，并且在啮合过程中载荷、滑动速度、摩擦系数是不断变化的，进而得到了弧齿轮热分析的方法.G.Deng[5]等利用实验的方法，利用热电偶测量直齿轮、斜齿轮在不同工作状态下的本体温度，提出了计算本体温度的方程，并研究进油温度、摩擦能量损失和冷却效率对齿轮本体温度的影响.

目前，国内外针对齿面温度预测的模型，大部分没有与实验结果进行对比证明其有效性；而且，对渐开线圆柱斜齿轮进行传动设计时，一些基本设计参数对齿面温度的影响也鲜有报道.本文针对此问题，考虑齿面与空气、润滑油之间的对流换热及齿轮副摩擦产生的热流量，建立斜齿轮温度场有限元模型，利用实验结果验证有限元分析模型的有效性；针对斜齿轮参数设计时的一些常用参数，如齿顶高系数、螺旋角、齿宽等定量的分析了这些设计参数对高速斜齿轮齿面温度的影响，从而为高速斜齿轮的抗胶合设计提供了依据.

1　有限元分析模型

对齿面温度场进行分析前，首先需要建立齿轮副有限元网格模型，然后对模型加载热边界条件.本文利用商业有限元软件ANSYS中的APDL语言对齿轮副进行参数化建模，而边界条件的设定则需考两部分：①轮齿与空气和润滑油的对流热；②摩擦产生的热流量.

1.1对流换热

根据D.P.Townsend[6]提出的理论，轮齿齿顶、齿面以及端面的对流换热系数是不同的，可根据公式（1）-（5）进行定义.

齿顶的对流换热系数如式（1）所示：

齿面的对流换热系数如式（2）所示：

齿轮端面的对流换热系数如式（3）所示：

其中，普朗特系数Pr和雷诺系数Re的定义分别如式（4）和式（5）所示：

式中，cf为润滑油的比热容；ρf为润滑油的密度；ff为润滑油的运动粘度；k为润滑油的热传导率；ω为齿轮的旋转速度；rc为齿轮端面任意点的半径；vc为节圆线速度；rc齿轮端面任意点的半径；hɑm为平均齿高.

本文齿轮润滑采用的是L-TSA汽轮机油，在40℃时相关的参数特性如表1所示，

表1　润滑油物理参数

1.2热流量密度

斜齿轮在高速状态下产生热量的主要原因是摩擦生热.轮齿表面的摩擦热流量由接触压力、齿面相对滑动速度和齿面摩擦系数决定的.为了计算方便，先建立无量纲线性坐标系，如图1所示.取啮合线为坐标轴，K为坐标的原点，Y为坐标轴上任意一点，KN2为正方向，则无量纲坐标Γy如式（6）所示：

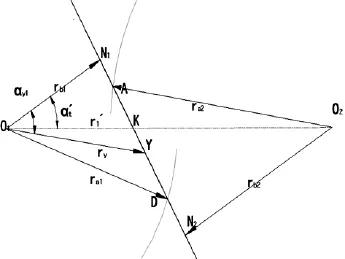
图1　无量纲线性坐标

其中，α′t为K点的压力角；αy1为啮合线上任意一点Y的压力角.

H.T.Lin等[7]指出，齿轮齿面任意啮合点Y处滑动摩擦热的计算公式如式（7）所示，

式中，Vk是K点齿轮相对滑动速度；σH是齿面的平均接触应力；γ为转化系数，一般取0.9.则平均接触应力σH表示为：

式中：Fbn为垂直于接触线的法向力；v1、v2为齿轮的泊松比；E1、E2为齿轮的弹性模量；L为接触线长度；R1、R2为接触点处的曲率半径.

齿轮在任意的接触点K处的主、从动轮的摩擦热流量分别为：

式中：qy1、qy2为主从动轮的热流密度；β为分配因子.

齿面的相对滑动速度为[8]：

式中：n1为主动轮的转速；db1为主动轮基圆直径；i为齿轮传动比；一般情况下，摩擦系数取f=0.05[9].

由于对有限元网格进行热边界条件加载时，同一个表面上无法同时加载对流换热系数和平均摩擦热流量，所以本文通过建立表面效应单元，将表面效应单元的单元号放入数组中并获得节点坐标，然后通过APDL语言对该点的啮合状态进行判断，从而计算出平均热流密度并进行加载.

2　有限元模拟结果和实验对比

为了验证建立的有限元分析模型的有效性，本节利用有限元模型对G.Deng等[5]的实验进行模拟，结果并与之对比.实验中斜齿轮参数如表2所示.实验测温的5个热电偶分别设在齿轮的1-5点，且位于连结点表面以下0.1mm处如图2中（a）图所示，点1-5的温度在60 s内以10 Hz的频率被测量直到达到恒定值，G.Deng等的实验测量得到的齿轮齿面温度如图2中（b）图所示：

表2　文献[5]齿轮参数

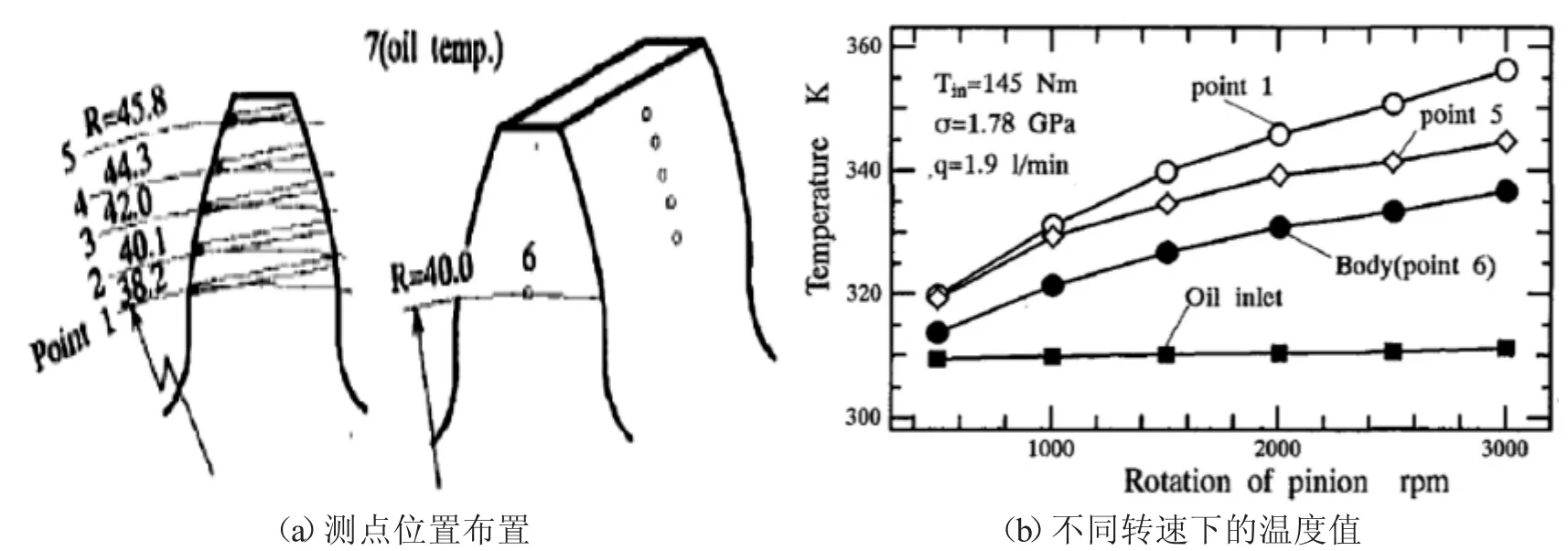
图2　实验测点布置位置及测量温度

有限元模型的输入参数和实验一致，进行齿面温度场分析，得到的小齿轮齿面温度场如图3所示.可以发现，齿面温度的最高点分布在轮齿啮入和啮出的位置，取同样的测点1和测点5，和实验测试结果进行对比.

图3　齿面温度场

当小齿轮转速在500-3 000 r/min时，测点1和测点5的温度如图4所示.可以发现，利用本文的有限元模型计算的温度和实验结果趋势上一致，即随着小齿轮转速的增加，本体温度也随之增加.两种方法预测的温度值较接近：当小齿轮转速在500 r/min时，齿面最高温度两者仅相差0.313%；当小齿轮转速在3 000 r/min时，两者最高温度相差5.67%.实验预测结果略高于有限元分析结果.两种方法的误差主要由于在有限元分析中，考虑的是一对无安装和制造误差的理想齿轮，而在实验测试时，由于齿轮不可避免的会有安装和制造误差，导致轮齿不平稳啮合，进而导致试验测试的齿面温度略高于有限元分析结果.有限元结果和实验值较接近，证明了本文提出的模型可以较为准确的预测斜齿轮的齿面温度.

图4　有限元分析齿面测点温度和实验测试温度对比

3　斜齿轮设计参数对齿面温度的影响

通过上节的对比验证了有限元分析模型的有效性，在本节将有限元模型应用于研究设计参数对齿面温度的影响.在斜齿轮设计时，需要给定斜齿轮的基本设计几何参数，因此，分析不同参数对齿面温度的影响可以为斜齿轮的抗胶合设计提供依据.在设计时，螺旋角、齿顶高系数、齿宽是影响胶合计算的主要因素，本节针对螺旋角、齿顶高系数、齿宽对齿面温度的影响进行有限元分析.

本文采用的斜齿轮参数如表3所示.

表3　本文齿轮参数

一般认为，齿顶高系数对胶合的影响较大，一般在设计时选取齿顶高系数.然而，在一些特殊情况，会选择采用长齿）或是短齿.本文首先分析齿顶高系数对斜齿轮齿面温度的影响.

通过齿轮温度场分析，得到不同齿顶高系数对齿面温度的影响.如图5所示为齿顶高系数分别为0.8和1.2时齿轮的温度场.当时，轮齿较长，此时齿面的最高温度Tmax为99.861℃，而最低温度Tmin为56.647℃；当采用短齿时，齿面最高温度Tmax降低为81.361℃，最低温度降低为Tmin为51.459℃.两者的温度相差达到18.5℃，温度增加达到22.74%.可见齿顶高系数对齿轮的温度场影响较大.

保持齿轮副的其他几何参数、载荷、转速等不变，只改变齿顶高系数时，齿面最高温度与齿顶高系数的变化情况如图6所示.可以发现，齿面最高温度随着齿顶高系数的增加而上升.在实际工程实践中，船用齿轮多为高速重载工况下工作齿轮，在齿轮副啮合过程中易发生胶合失效现象，因此，船用齿轮设计选择齿顶高系数时，宜选用较小的短齿齿轮.本文的结论和设计经验[10]相符.

图5　不同齿顶高系数的斜齿轮的温度场

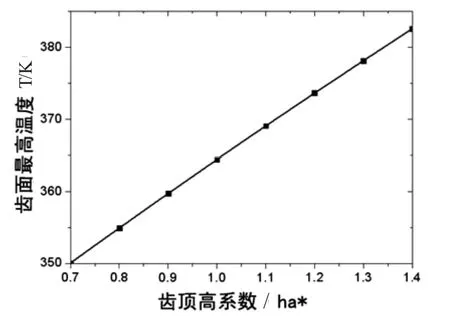
图6　测点温度随齿顶高系数的变化趋势

影响斜齿轮齿面温度的几何参数中，螺旋角β也是一个重要的因素.若螺旋角β过小，斜齿轮的传动的优点不能充分的显示，若β过大，则将产生过大的轴向力.因此，在设计时一般选取渐开线斜齿轮的β=8°～25°.利用有限元分析，得到如图7所示的齿面最高温度与螺旋角β的关系曲线.可以发现，当螺旋角增加时，齿轮本体温度总体趋势是下降的，但中间会有上升、再下降的波动.这是因为当螺旋角增大，其他参数不变的时，啮合线长度增长，单位线载荷减少，从而导致齿面温度的总体趋势减少；而螺旋角的改变又会导致斜齿轮同时啮合齿数的区域发生改变，当啮合齿数少的区域出现在齿轮中部或者是齿根处，由于离端面和齿顶远，导致与外界的热交换差，所以即使螺旋角增大，齿面局部区域的温度也会略有增加.

图7　测点温度随螺旋角的变化趋势

图7为齿面最高温度随着齿宽的变化情况.从图中看出，随着齿宽的增加，总体趋势上轮齿齿面的最高温度上下波动，但是总体上是趋势是增加的，最大温差达到了11.788℃，增加达到了13.6%.所以，齿宽对与齿轮表面温度也略有影响，长宽齿轮的冷却效果较差，增大齿宽对齿面的胶合不利.

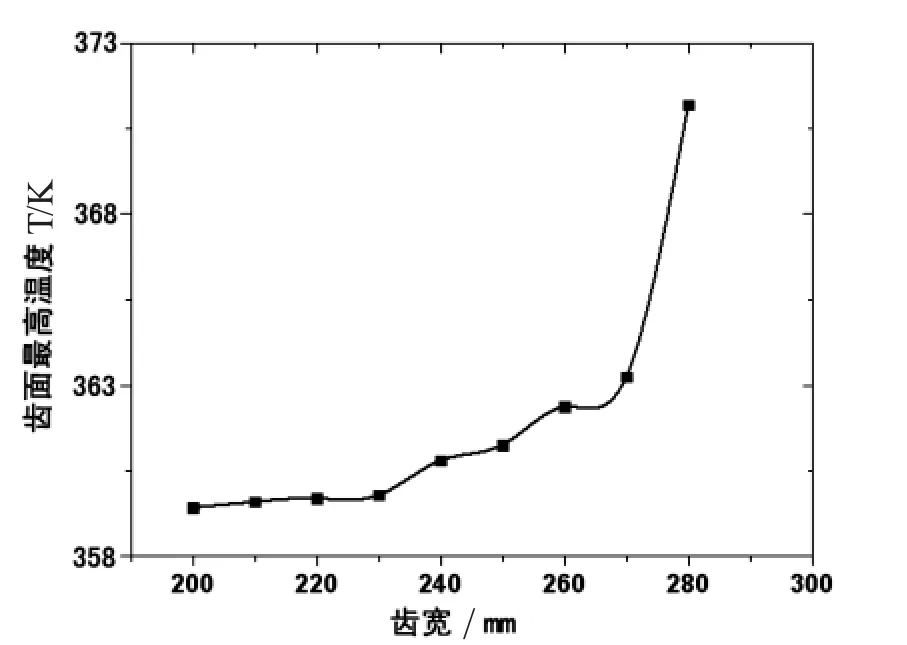
图8　测点温度随齿宽的变化趋势

4　结论

本文建立了斜齿轮温度场有限元分析模型，考虑了对流换热和摩擦热，和实验对比验证了有限元模型的有效性，并将模型进一步分析基本设计参数对齿面温度的影响，得到的结论如下：

（1）本文建立的有限元分析模型可以较准确的预测齿面的温度，和实验结果相比，最大误差在5.67%.

（2）齿顶高系数对于齿面温度的影响较大，齿面温度随着齿顶高系数的增加而增加，最大相差22.74%.

（3）齿面整体温度随着螺旋角的增加而增加，然而，齿面的局部温度（啮入啮出位置）却随着螺旋角的增加而波动.

（4）随着齿宽的增加，总体趋势上轮齿齿面的最高温度增加.

[1]TOBE T，KATO M.A study on flash temperatures on the spur gear teeth[J].Journal of Engineering for Industry，1974，2：78-84.

[2]WANG K L，CHENG H S.A numerical solution to the dynamic load，film thickness and surface temperatures in spur gears，Part II：Analysis[J].Journal ofMechanical Design，1981，103：121-124.

[3]李润方，唐庆平.运转过程中轮齿耦合热弹性接触有限元分析[J].齿轮，1989，1（13）：98-103.

[4]HANDSCHUH R F，KICHER T P.A method for thermal analysis of spiral bevel gears[J].Journal of Mechanical Design.1996，118（4）：580-585.

[5]DENG G，KATO M，MARUYAMA N，et al.Initial temperature evaluation for flash temperature index of gear tooth[J].Journal ofTribology.1995，117（3）：476-481.

[6]TOWNSEND D P，AKIN L S.Analytical and experimental spur gear tooth temperature as affected by operating variables[J].Journal ofMechanical Design，1981，103（l）：219-226.

[7]LIN H T，LIN L K，LI C.Heat transfer from a rotating cone or disk to fluids of any Prandtl number[J]. Communication in Heat and Mass Transfer，1987，14（3）：323-332.

[8]田兴，李威.少齿数非对称齿轮主动设计与温度场分析[J].哈尔滨工程大学学报，2013，34（7）：907-912.

[9]李润方.齿轮传动的刚度分析和修形方法[M].重庆：重庆大学出版社，2002.

[10]DENG G，KATO M，MARUYAMA N，et al.Initial temperature evaluation for flash temperature index of gear tooth[J].Journal of Tribology.1995，117（3）：476-481.

[11]朱孝录.齿轮传动设计手册[M].北京：化学工业出版社，2010.

Effect of Design Parameters of High-Speed Helical Gears on Flank Temperature

FAN Yilong,FU Kunkun,HUO Zhaobo,YU Dongyang
（703 institute of CSIC,Ship and HearyIndustry,Harbin 150078,HeiLongjiangChina）

In this study,finite element（FE）model of helical gear was developed to evaluate their surface temperature.In this model,heat convection between gear tooth and air as well as lubricant was considered,and heat was generated due to gear friction.The model was validated by comparing to the measured temperature of helical gears in an existing experiment.Finally, the effect of gear design parameters on helical gear temperature was determined by the current FE model.It was shown that the predicted temperature by the current FE model is consistent with the measured temperature in experiment,and the maximum error is within 5.67%. Moreover,gear temperature was increased by increasing addendum coefficient and face width. However,gear temperature was fluctuated with the change of helix angle.This work provides aguidance for the design of high-speed helical gears.

helical gears；surface temperature；FE；design parameters

TH132.41

A

1001-4217（2016）01-0065-08

2015-07-04

范一龙（1988—），男，汉族，黑龙江省哈尔滨人，中国船舶重工集团公司第七○三所硕士研究生，研究方向：机械传动和齿轮动力学.Email：fanyilong12345@163.com

船舶动力基础科研项目（MPRD-MG0206）