具有非线性脉冲效应和混合时滞的神经网络的指数同步
蒲 浩,蒋海军,刘衍民,张转周
(1.遵义师范学院 数学与计算科学学院, 贵州 遵义 563002;2.新疆大学 数学与系统科学学院,乌鲁木齐 830046)
具有非线性脉冲效应和混合时滞的神经网络的指数同步
蒲浩1,蒋海军2,刘衍民1,张转周1
(1.遵义师范学院 数学与计算科学学院, 贵州 遵义563002;2.新疆大学 数学与系统科学学院,乌鲁木齐830046)
研究了一类具有非线性脉冲效应和混合时滞的神经网络的指数同步。 通过李雅普洛夫稳定性理论和一些不等式方法,利用p-范数得到了新的指数同步的充分条件。和之前的脉冲效应是线性函数的结论相比较,消除了对线性脉冲效应系数γij∈[0,2]的限制,适用范围更广泛。
指数同步;神经网络;混合时滞;非线性脉冲效应;p-范数
近年来,神经网络指数同步在许多科学领域中的理论研究和实践应用中有着广泛的应用,例如,在信号和影像传递过程、联想记忆、生态系统、组合优化、军事领域、人工智能系统等。为此,许多学者对神经网络指数同步进行了广泛的研究[1-4]。
神经网络的同步不仅受到外界的干扰,而且受到自身因素的影响。例如:信号在不同的神经元之间的传递过程中受到外界的干扰,出现了扰动时滞;信号在不同的神经元之间的传递速度和转换速度是有限的,从而出现了信号传递的滞后现象[5-6],该现象会影响神经网络的信号传递同步。
在神经网络中,信号在不同神经元之间的传递过程中受到外界的干扰会引起信号的短暂波动,即脉冲现象。许多研究者对具有脉冲效应的神经网络同步问题进行了广泛的研究[7-9]。但这些研究所考虑的脉冲效应主要是线性函数,比如文献[7-9]考虑的脉冲效应是线性函数Δxi(tk)=-γikxi(tk) 且γij∈[0,2],但在实际的神经网络中出现的脉冲效应系数不只局限于γij∈[0,2]。
1 模型和预备知识
考虑如下的具有非线性脉冲效应和混合时滞的神经网络模型:
(1)

系统(1)的初值条件为

(2)
对于系统(1),假设:

把系统(1)作为主驱动系统,为了同步,引入如下响应系统:
(3)
其中:ui(t)表示如下的外部输入控制:
(4)
kij(i,j∈I)是一个常数。
响应系统(3)的初值条件是:yi(s)=φi(s),s∈[-τ,0],i∈I,其中φi(s)=(φ1(s),φ2(s),…,φn(s))T∈C([-τ,0],Rn),定义误差系统为ei(t)=yi(t)-xi(t)。由驱动系统(1)和响应系统(3),可以得到如下的误差系统:
(5)
(H2)对任意的i∈I,λi-ξi-αi-βi>0成立。
构造一个函数列:
当εi=0时,根据假设(H2),有Fi(0)=λi-ξi-αi-βi>0,i∈I,而
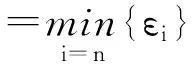
定义1如果存在常数A≥1使得
(6)

2 辅助引理
引理 1[10]对任意的非负实数a和b,不等式
(7)
成立。
为了证明后面主要结论的需要,由引理(1)经过计算可知:
(8)
(9)
(10)
(11)
成立。

对任意的(x1,x2,…,xn)∈Rn,(y1,y2,…,yn)∈Rn,i∈I和k∈Z+成立。

3 主要结果
定理1如果(H1)~(H4)成立,在恰当的外部控制输入ui(t)(i∈I)的条件下,则驱动系统(1)和响应系统(3)是全局指数同步的。
证明构造如下形式的Lyapunov函数:
(12)
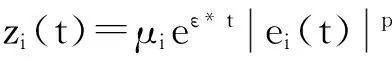
(13)
当t=tk时,由假设(H3)-(H4)有如下结果
(14)
定义
(15)
由式(12)~(15)可知:z(t)≤V(t)≤ρk-1V(tk-1)≤ρ1ρ2,…,ρk-1V(0),对t∈(tk-1,tk],k∈Z+,ρ0=1。由假设(4)可知:ρk≤e(tk-tk-1),k∈Z+, z(t)≤eα(t1-0),…,eα(tk-1-tk-2)V(0)≤eαtV(0),t∈(tk-1,tk],k∈Z+。结合前面的计算,有下列不等式成立:
(16)
当t=0时,由式(12)可知
(17)
由式(16)和(17)可知
(18)
由式(18)可知

说明驱动系统(1)和响应系统(3)是全局指数同步的。
4 推论
若在系统(1)中的脉冲函数是如下的线性函数:Δxi(tk)=γikxi(tk) 时,则有
根据定理(1),有如下推论成立:
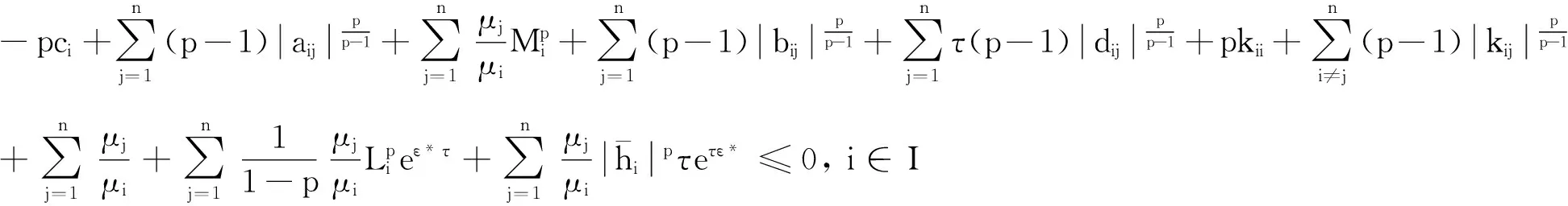

[1]LIANGJ,WANGZ,LIUX.OnSynchronizationofCoupledDelayedNeuralNetworks[M].[S.l.]:RecentAdvancesinNonlinearDynamicsandSynchronization,2009:117-149.
[2]CHENGC,LIAOT,YANJ,etal.ExponentialSynchronizationofAClassofNeuralNetworksWithTime-VaryingDelays[J].IEEETransSyst,ManandCybernetics,PartB:Cybern,2006,36(1):209-215.
[3]YANGXS,CAOJD,YUWW.ExponentialSynchronizationofMemristiveCohen-GrossbergNeuralNetworkswithMixedDelays[J].CognitiveNeurodynamics,2014,8(3):239-249.
[4]WANGK,TENGZD,JIANGHJ.AdaptiveSynchronizationinanArrayofLinearlyCoupledNeuralNetworkswithReaction-DiffusionTermsandDelays[J].CommumnicationinNonlinearScienceandNumericalSimulation,2012,17(10):3866-3875.
[5]YANJ,LINJ,HUNGM.OntheSynchronizationofNeuralNetworksContainingTime-VaryingDelaysandSectorNonlinearity[J].PhysLettA,2007,361:70-77.
[6]YUJ,HUC,JIANGHJ,etal.ExponentialLagSynchronizationforDelayedFuzzyCellularNeuralNetworksviaPeriodicallyIntermittentControl[J].MathematicsandComputersinSimulation,2012,82(5):895-908.
[7]SHENGL,YANGHZ.ExponentialSynchronizationofaClassofNeuralNetworkswithMixedTime-VaryingDelaysandImpulsiveEffects[J].Neurocomputing,2008,71(16):3666-3674.
[8]YANGYQ,CAOJD.ExponentiallagSynchronizationofaClassChaoticDelayedNeuralNetworkswithImpulsiveEffects[J].PhysicaA,2007,386:492-502.
[9]FENGXM,ZHANGFQ,WANGWJ.GlobalExponentialSynchronizationofDelayedFuzzyCellularNeuralNetworkswithImpulsiveEffects[J].ChaosSolitionsFractals,2011,44(1):9-16.
[10]YUJ,HUC,JIANGHJ,etal.ExponentiallagSynchronizationforNeuralNetworkswithMixedDelaysviaPeriodicallyIntermittentControl[J],Chaos,2010,20(2):023108-023115.
(责任编辑何杰玲)
Exponential Synchronization of Neural Networks with Nonlinear Impulsive Effects and Mixed Time Delays
PU Hao1, JIANG Hai-jun2, LIU Yan-min1, ZHANG Zhuan-zhou1
(1.School of Mathematics and Computational Science,Zunyi Normal College, Zunyi 563002, China;2.College of Mathematics and System Sciences, Xinjiang University, Urumqi 830046, China)
Exponential synchronization of neural networks with nonlinear impulsive γij∈[0,2]effects and mixed time delays was discussed. By Lyapunov stability theory and inequality techniques, some new and useful sufficient conditions on the exponential synchronization were obtained based onp-norm. Compared with recently years of linear impulsive effects results about neural networks synchronization, our results remove the restrictions that the impulsive gain γij∈[0,2], so our results are more general.
exponential synchronization; neural network; mixed time delay; nonlinear impulsive effects;p-norm
2016-03-12
国家自然科学基金资助项目(71461027);贵州省计划科技项目(黔科合LH字[2015]7053号,黔科合LH字[2015]7005)
蒲浩(1986—),男,甘肃天水人,硕士,主要从事神经网络同步研究,E-mail:puhao2100@163.com。
format:PU Hao, JIANG Hai-jun, LIU Yan-min,et al.Exponential Synchronization of Neural Networks with Nonlinear Impulsive Effects and Mixed Time Delays[J].Journal of Chongqing University of Technology(Natural Science),2016(9):143-150.
10.3969/j.issn.1674-8425(z).2016.09.024
O175.1
A
1674-8425(2016)09-0143-08
引用格式:蒲浩,蒋海军,刘衍民, 等.具有非线性脉冲效应和混合时滞的神经网络的指数同步[J].重庆理工大学学报(自然科学),2016(9):143-150.

