基于原始历史文献的大学数学教学模式研究与实践

刘宝宏

(国防科学技术大学　信息系统与管理学院，湖南　长沙　410073)



基于原始历史文献的大学数学教学模式研究与实践

刘宝宏

(国防科学技术大学信息系统与管理学院，湖南长沙410073)

在数学教学中融入数学史的相关内容是目前高校数学教学的普遍做法，但将历史文献作为主线的数学教学还不多见。本文提出了基于原始文献的数学教育(PHM2E)，给出了PHM2E的教育理念、体系框架、关系模型和过程模型。以原始数学文献为基础组织教学过程，将加深对数学的理解，促进学生高阶能力的培养。通过建构式、发现式学习，充分利用原汁原味的数学文献来研究数学，探索数学概念的发生、发展过程，学习数学大师的思维方式，探索解决问题的方法，重走大师之路，主动发现新知，充分发挥数学在素质教育中的作用。

原始文献；教学模式；数学教学；建构主义；发现式学习

一、 引言

数学是一切自然科学、技术科学乃至人文科学的基础，它是受教育者在校学习时间最长的学科之一。从大学数学教学的现状来看，随着现代数学的大发展，各门数学课程的知识体系都十分复杂，内容也十分丰富。目前国内大学的数学教学普遍采用系统的形式化推理方法，其讲授模式基本上按照“定义—定理—证明—应用”的模式进行。由于强调计算和证明，对概念的来龙去脉关注不够，学生在学习过程中记住了大量的概念和定理，但对数学的认识却比较肤浅，从而导致数学在培养高阶能力方面的作用发挥不足。在数学教学过程中，融入数学史的教学在一定程度上弥补了上述不足。但目前的数学史教学通常只是将历史回顾和历史轶事作为枯燥的数学教学的点缀。这种点缀固然是必要的，但还很不充分。

本文在教学实践的基础上，提出以原始数学文献为基础去组织教学过程，通过原始数学文献和现有各种教学模式的融合来提高大学数学的教学效果，我们将其称之为基于原始文献的数学教育(PHM2E，Primary Historical Material-Based Mathematical Education)。这里原始文献是指数学家在提出数学概念、建立数学理论或证明数学定理时发表的原始文献，以及某个领域的代表性数学文献。我们这里强调的不是将数学史作为一门学科来讲授，也不是如何在数学教学中穿插数学史教学，而是如何充分利用数学原始文献，通过原汁原味的数学文献来研究数学，探索数学概念的发生发展过程，学习数学大师的思维方式，探索解决问题的方法，重走大师之路，充分发挥数学在素质教育中的作用。本文中的PHM2E主要针对高等院校的教学活动，其基本理念对于高级中学、初级中学、以及职业中学的教学仍然具有重要的借鉴意义。本文提出的教学模式主要用于数学教学，由于数学的特殊性，可以在教学中系统使用本方法，其他学科一般难以用历史素材贯穿教学过程，但本文所提出的教育理念对于物理、化学、计算机等其他学科也具有一定的借鉴意义。

二、国内外研究现状

在现代意义的大学出现之前，很多大数学家都是通过研究前人的原始著作学习数学的。在数学家提出数学思想和数学方法的文献中，有着丰富的资源等待我们去挖掘，有着很多现在数学教材中未能体现的创新思想值得我们去学习。但是，随着数学知识体系的日益庞大和对数学知识的不断梳理和加工，原始历史文献开始淡出大学课堂，淹没在浩如烟海的数学教材之中。

(一)高等院校数学教育的现状

由于数学在科学研究中的基础性地位，数学的教学问题在国际上一直受到广泛重视，数学教育的改革也在持续进行中。广大教师和研究者们一直在努力改进教学方法，寻找更好的教授数学的手段[1]。从20世纪80年代开始，国内高校也广泛开展了以教学内容和课程体系为核心的数学教学改革。

当前数学教学的一个特点是注重形式化的演绎数学思维的训练。这一点在各种数学教材中尤为明显。以离散数学课程为例，通过对国内外30余本离散数学教材的研究，我们发现：所有这些教材都遵循相似的体例和编写模式，所有的讲授都按照传统模式进行。教学内容都是按照现代的观点重新组织、精心包装的，通常按逻辑顺序从定理到定理或从公式到公式地组织内容，而重要的数学思想和思维方法却淹没在概念定理之中。学生在教学活动中处于被动接受的地位，陷入枯燥的逻辑证明和计算分析，丧失了学习数学的兴趣，更谈不上通过数学培养学生的思维习惯和创新能力。

(二)数学史与数学教育结合的研究

早在18世纪，法国实证主义哲学家、社会学创始人孔德就提出，对学生的教育应按历史上人类受教育的方式和顺序进行。瑞士著名教育家裴斯泰洛奇、德国著名教育家弗罗贝尔等人都持有类似的观点[2]。19世纪英国著名数学家德·摩根不仅强调数学史对数学研究的重要性，而且强调数学教学中应遵循的历史次序[3]。20世纪上叶，一些欧美数学家，如卡约黎、庞加莱、史密斯等都大力提倡数学史在数学教学中的运用。当代著名数学家和数学史家克莱因批评只注重逻辑严密性的数学教材和教学活动，强调数学家奋斗的经历对学生的教育作用[4]。20世纪70年代，HPM(History and Pedagogy of Mathematics)成为一个独立的学术研究领域[5]。今天，HPM已成为国际数学教育的新思潮之一。

数学史教育在我国始于20世纪50年代，当时只是在个别院所进行了不同形式的尝试，例如中国科学院自然科学史研究所开始培养数学史研究生，一些师范院校对数学教师和学生开设数学史讲座或报告等。进入20世纪90年代，数学史教育得到广泛普及，1994年，全国数学史学会第四届理事会将“数学史教育”作为一项重要的内容[6]。同时，国内也广泛开展了将数学史融入课堂教学的研究和实践活动。但总体上，我国数学教育中对数学史的重视程度与西方国家相比还有一定差距。

(三)原始历史素材在数学教学中的应用研究

数学史知识与数学教学的具体结合一直是HPM学者们的研究目标之一。1995年美国数学史及其在教学中的运用研究所( the Institute in the History of Mathematics and its use in Teaching, IHMT) 将“历史模块项目”(Historical Module Project，HMP)作为其重要工作之一[7]。HMP项目研究在组合学、指数与对数、函数、几何证明、长度、面积和体积、线性方程、负数、多项式、统计、三角等教学模块中融入数学史。但HMP项目并不强调使用原始的数学文献进行数学教学，且其教学对象基本上是中学生。

在美国国家自然科学基金会的支持下，新墨西哥州立大学、奥多明尼昂大学、科罗拉多州立大学普韦布洛分校联合开展了“基于第一手历史资料的离散数学和计算机科学学习”研究[8-9]。该研究从2007年开始，2008年开始又资助了二期研究，目前该项研究还在进行。这是国际上少数将原始数学文献系统引入课堂教学的工作之一。

总体来看，由于学时限制、评价方式以及教师自身对原始数学文献掌握不足等原因，国内高校在这方面的研究和实践还比较缺乏。将数学史融入数学教学的基本模式仍然局限于“讲故事”，对历史材料的运用还不够充分。

三、PHM2E教学模型

作者在长期离散数学教学实践的基础上[10]，提出基于原始历史文献的数学教学模型。本节对PHM2E的体系结构、关系模型和过程模型进行系统介绍。

(一)建构主义视角下的PHM2E

数学教学不应只是简单地将知识灌输给学生，而是要鼓励学生探索未知、发现知识、批判性思考。学习的过程是学生自我构建理解的过程，是自我发现、自我提升的过程。

按照建构主义的观点[11-12]，在基于原始数学文献的数学教学实践过程中，可以从以下几个方面实施PHM2E：

1.理解学习者：教师要对学习者有深刻的理解，明确学生已有的知识基础、理解学生在解决问题过程中可能会遇到的困难，理解学习者在协作过程中可能出现的障碍、理解学习者的潜能，理解每个学习者的特点和学习风格，以便有效组织教学过程。

2.理解学习过程：PHM2E学习过程要通过讲授与研讨结合、课上与课下贯通、线上与线下协同、经典与现代互补等方式构建科学的教学模式。教师要根据教学内容和学生特点，控制文献的输出和教学的进展，包括文献的分段给出、基于有限提示的教学推进、质询式推进、帮促式推进等。

3.创设支持性和具有挑战性的学习环境。一方面，教师应为学生的探索提供知识上的支持、方法上的指导、心理上的鼓励、思路上的点拨；另一方面，教师应激发学生的学习热情，鼓励学生的创造性思维，问题的设置应具有一定的挑战性。

4.建立有益的学习伙伴关系：教师应为学生营造有效的交流沟通氛围，学生之间形成学习共同体，一起制定计划、解决问题、评估结果。更重要的是，在学习过程中，教师不应是高高在上的权威，而是作为学生的伙伴共同探寻知识。另外，还要将做出数学发现、撰写原始文献的数学家作为虚拟的伙伴，作为学习的向导贯穿学习始终。

5.密切联系社会和文化情境：教师要引导学生理解数学家当初解决问题时的历史背景、数学体系和文化情境。要帮助学生认识数学发现的历史局限性。同时，要鼓励学生在现在数学体系和社会背景下重构数学文献提供的概念和理论。

(二)PHM2E体系框架

在基于原始数学文献的学习过程中，学习的重点不再是枯燥的课本知识，而是数学家解决问题的思路。学习的过程不再是被动接受，而是主动探索解决问题的方法。学习结果是多元的，包括知识的扩充，创新能力的提高，个性品质的培育，协作意识的培养。学习的方式也是多元的，包括自学、讨论、协作、引导等。此时，学生是学习过程的主体，教师是整个学习过程的引导者、辅助者、控制者。PHM2E的框架如图1所示。

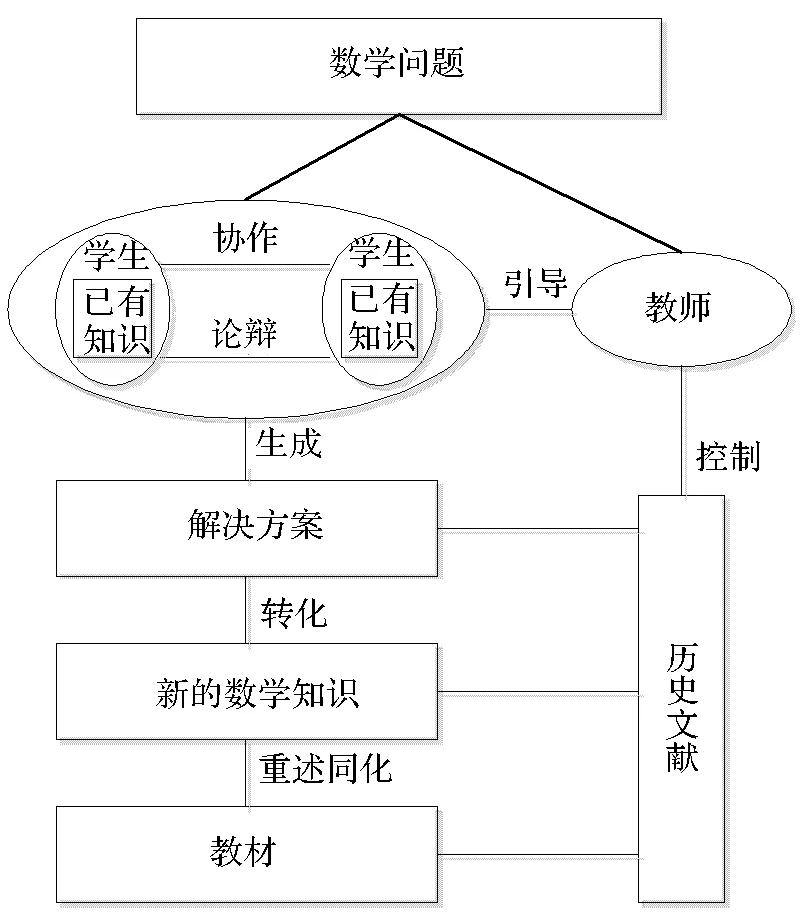
图1　PHM2E 框架模型

(三)PHM2E关系模型

在PHM2E中涉及学生、教师、文献、教材、旧知、新知等多种要素，以及学生与教师、旧知与新知、文献与教材、学生与文献等各种关系。各要素之间的关系如图2所示。下面我们对其中的主要关系做进一步阐述。

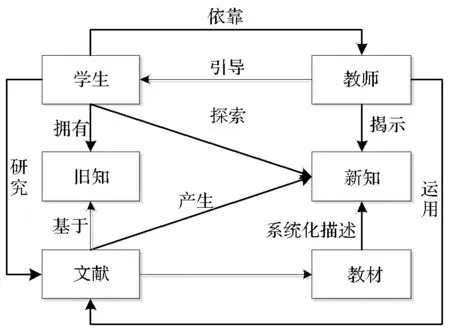
图2　PHM2E 关系模型

1.教师与学生的关系：以学生为学习主体，以教师为课堂主导

在PHM2E中，学生不再是被动的知识接受者，教师不再是数学的传道者。学生成为学习的主体，成为解决问题、形成新知的主动要素。但是，教师仍然是整个课堂的主导者，在教学实施过程中负责学习节奏的控制，研讨过程的协调，探索障碍的扫除。

2.已有知识和新知识的关系：以已有知识为基础，以新知识的形成目标

学生在学习数学大师原始文献的过程中，必然要基于已有知识，这些知识是学生探索新知的基础。学生要在文献基础上结合已有知识进行拓展研究。在PHM2E中新知识是学生自己发现的，学习新知识的过程就是解决问题的过程，就是和数学大师进行交流的过程，就是重走大师路的过程。

3.教材与文献的关系：以文献为主线，以教材为落脚点

原始文献给出了数学家在特定的历史背景和数学背景下解决问题的完整过程。这个过程作为主线贯穿学生学习过程的始终。当学生在数学大师的指引下走完这个过程之后，还要回到教材，从现代数学体系的角度反观历史文献，包括：用现代数学的观点重述文献中的概念、定理；从现代数学的角度讨论文献的不足，研究解决问题的其他方法；以原始文献为背景，进一步理解教材中的概念和定理。

(四)PHM2E过程模型

从过程的角度，PHM2E可以分为3个阶段，其中教学准备阶段是基础支撑，教学实施阶段是成败关键，教学总结阶段是有效提升。下面进一步阐述各阶段的关键环节(如图3所示)。

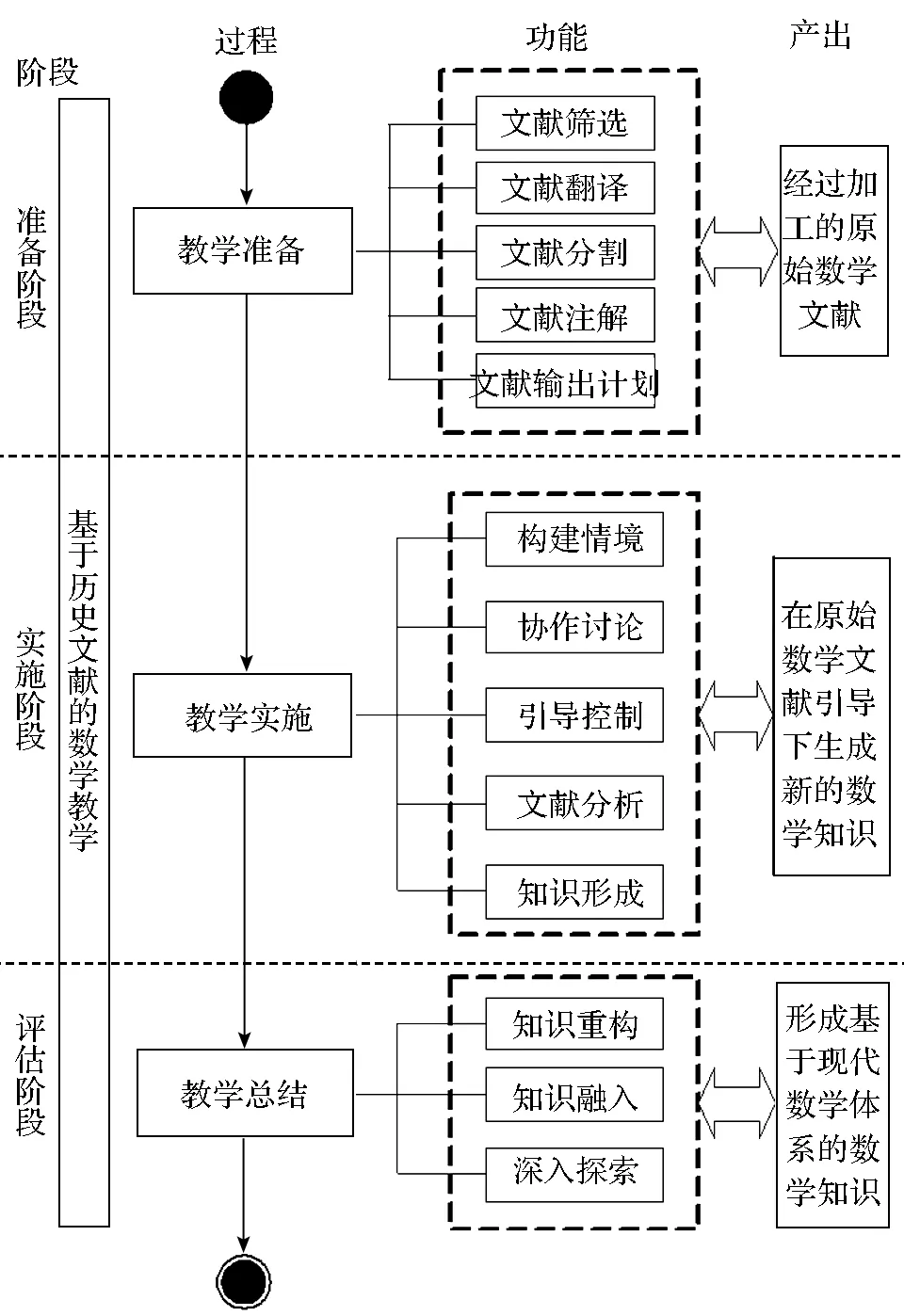
图3　PHM2E 过程模型

1.教学准备阶段的文献加工

为了将原始文献用于教学，需要按照教学的目的、教学内容、学生的接受能力选择文献，然后对其进行再加工。文献加工包括文献的翻译、注释、缩减、切割等。对不同层次的学生文献加工的程度和方法不同。此项工作是整个PHM2E的基础性工作，关系到教学的成败，也是教师花费精力最多的环节。

2.教学实施阶段的课堂控制

教师作为PHM2E的导演，要根据教学的进展和课堂实况做好控制协调工作。根据教学内容、学生特点，控制文献的输出和教学的进展，灵活使用课前分发文献、分段给出文献、基于有限提示的教学推进、质询式推进、帮促式推进等多种方式。教师要把握好文献输出的节奏，引领学生思路的同时激发学生的创造性。教师要把握好建构的节奏，避免陷入低效的讨论。教师要及时扫除建构的障碍，确保教学活动的顺利进行。

3.教学总结阶段的知识重构

不可回避的是，教科书上的数学知识都是按照现代数学体系重构的，为了教学的方便对知识进行了重新编排。通过原始文献学到的数学知识要与现代数学体系同化，要融入学生已有的数学知识体系中，要进一步转述为现代数学的概念定理，要在现代社会背景下讨论其实际应用。

四、总结

我们从2012年开始基于原始文献的离散数学教学工作。实践表明，教学效果是多方面的。不但学生的成绩得到了提高，更重要的是学生对离散数学的兴趣更浓了，学习的主动性增强了。历史文献在培养学生高阶能力方面的作用是明显的，对学生的影响是深远的。基于原始文献的大学数学教学方法研究和实践将更新教育理念，提高教学效果，增强学生对知识的理解，加深对数学的认识，培养科学精神，促进学习者解决问题、自主创新、批判思维、信息运用、团队协作、兼容并蓄、自我管理等高阶能力的发展。

虽然我们以大学数学为背景，其基本理念和方法可以扩展到中学、研究生的教学。同时，在实施过程中应注意PHM2E的适用性。PHM2E不可能在任何情况下都是适用的。有些课程可以完全适用PHM2E教学，有些课程只能部分应用PHM2E教学；在专科、本科和研究生层次PHM2E应用的程度应该有所不同，要注意把握PHM2E对不同层次教学的适用度。最后需要指出的是，教师的素质是决定PHM2E效果的重要因素。由于很多一线教师对原始数学文献缺乏研究，对PHM2E的实施造成一定困难。教师培训对PHM2E教学质量的提高具有重要意义。

[1]Fauvel J，van Maanen J. A (eds). History in Mathematics Education [M].Dordrecht：Kluwer Academic Publishers，2000：291-328.

[2]汪晓勤，欧阳跃.HPM的历史渊源[J].数学教育学报，2003(3)：24-27.

[3]汪晓勤，张小明.HPM研究的内容与方法[J].数学教育学报，2006(1)：16-18.

[4]Kline M．Logic Versus Pedagogy[J].American Mathematical Monthly，1970 (3)：264-282．

[5]俞宏毓.高师院校数学史教学改革初探[J].绍兴文理学院学报：自然科学，2010(7)：91-94.

[6]俞宏毓.高师院校数学史教学改革初探[J].绍兴文理学院学报：自然科学，2010(7)：91-94.

[7]汪晓勤，张小明.HPM研究的内容与方法[J].数学教育学报，2006(1)：16-18.

[8]Barnett J，Bezhanishvili G，Leung H，et al. Historical Projects in Discrete Mathematics and Computer Science，Resources for Teaching Discrete Mathematics[M].Washington D C：Mathematical Association of America，2009：1-3.

[9]Barnett J，Lodder J，Pengelley D，et al. Designing Student Projects for Teaching and Learning Discrete Mathematics and Computer Science via Primary Historical Sources [M]. Washington D C：Mathematical Association of America，2011：1-24.

[10]Liu Baohong.Instructional Innovation of Discrete Mathematics for Non-Computer professional Students [C]// Zhou X.Proceedings of the 3rd International Conference on Education Technology and Training，New York：IEEE，2010：145-148.

[11]约翰·桑切克.教育心理学[M].2版.周冠英，王学成，译.北京：世界图书出版公司，2007：7-8.

[12]钟志贤.大学教学模式革新：教学设计视域[M].北京：教育科学出版社，2008：170-173.

(责任编辑：陈勇)

A Research on Primary Historical Material-Based Mathematical Education and Its Application

LIU Bao-hong

(CollegeofInformationSystemandManagement，NationalUniversityofDefenseTechnology，Changsha410073，China)

Integrating mathematical history into mathematical education is a common practice in universities，but it is rare to use historical material as the main clue during the teaching activities. An education pattern named Primary Historical Material-based Mathematical Education (PHM2E) is proposed in this paper. The educational concepts，system framework，relational model and process model are given in this paper. The teaching activity is organized based on original mathematical literatures in PHM2E. This pattern can deepen the students’understanding of mathematics and improve their high-order capability. Through constructive and discovery study using original literatures，students can explore the development process of mathematical concepts and study the mathematicians’pattern of thinking. They can explore the methods of solving problems and discovery new knowledge initiatively.

primary historical material；teaching pattern；mathematical education；constructivism；discovery learning

2015-06-27

2014年度湖南省教改课题“基于历史视域的大学数学教学模式改革与实证研究”

刘宝宏(1974-)，男，天津人。国防科学技术大学信息系统与管理学院副教授，博士，主要从事复杂系统建模与仿真，研究型教学的理论与实践等方面研究。

G642

A

1672-8874 (2016) 03-0084-05