关于洛必达法则求极限的教学总结

张 蕾

（山东职业学院，山东 济南 250000）

关于洛必达法则求极限的教学总结

张 蕾

（山东职业学院，山东 济南 250000）

本文结合教学实际对洛必达法则及其在求未定式极限方面的应用进行了分析，同时还分析了学生易错的洛必达法则求函数极限失效的情况。

洛必达法则；未定式；极限

求极限是微积分中的一项非常基础和重要的工作。教学中发现对于普通的求极限问题，学生解决起来问题不大，但是对于形如的7种未定式，学生虽然能联系到洛必达法则，但是经常出错。

一、洛必达法则及应用

（一）洛必达法则

若函数f（x）与函数g（x）满足下列条件：

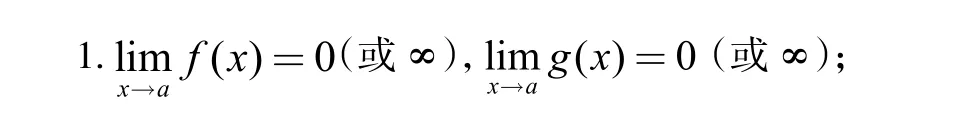
2.f（x）与g（x）在x=a点的某个去心邻域内可导；

洛必达法则所述极限结果对下述六类极限过程均适用：

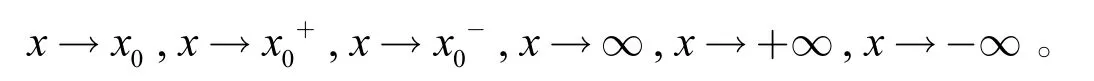
（二）洛必达法则的应用

1.基本类型：未定式直接应用法则求极限

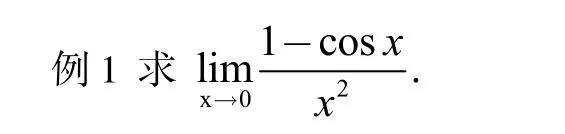
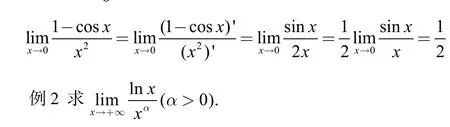
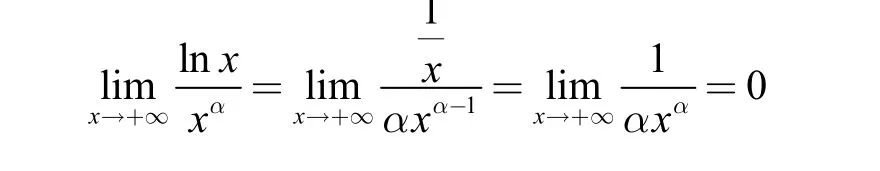
2.未定式的其他类型：0·∞、∞-∞、00、∞0、1∞型极限的求解

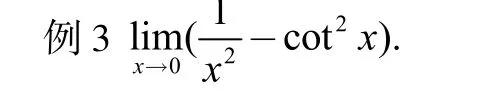
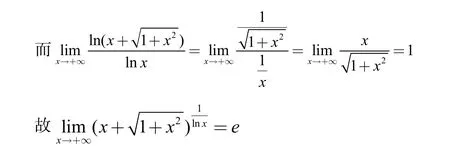
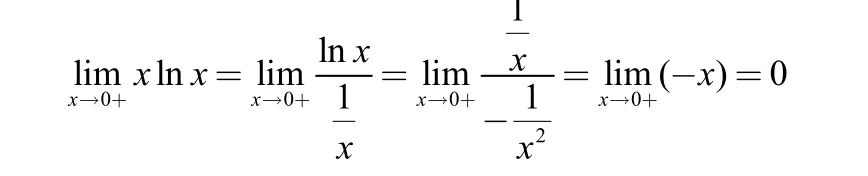
解：这是00型未定式，由对数恒等式知，xx=exInx，运用例8可得

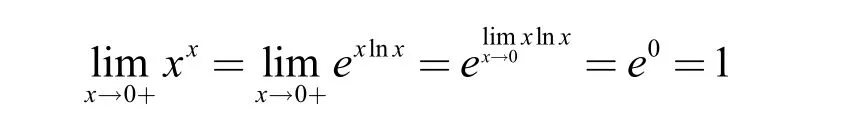
二、洛必达法则对于实值函数的失效问题

洛必达法则可谓是在求不定式极限中作用最为显赫的一种方法，当然，它也有失效的时候。“失效”的原因则是因为题目本身不满足可以使用洛必达法则的几个条件。所以，在要使用洛必达法则时，要检验该题目是否符合洛必达法则条件，洛必达法则失效的基本原因有以下几种。

（一）使用洛必达法则后，极限不存在（非∞），也就是不符合洛必达法则的条件（3）

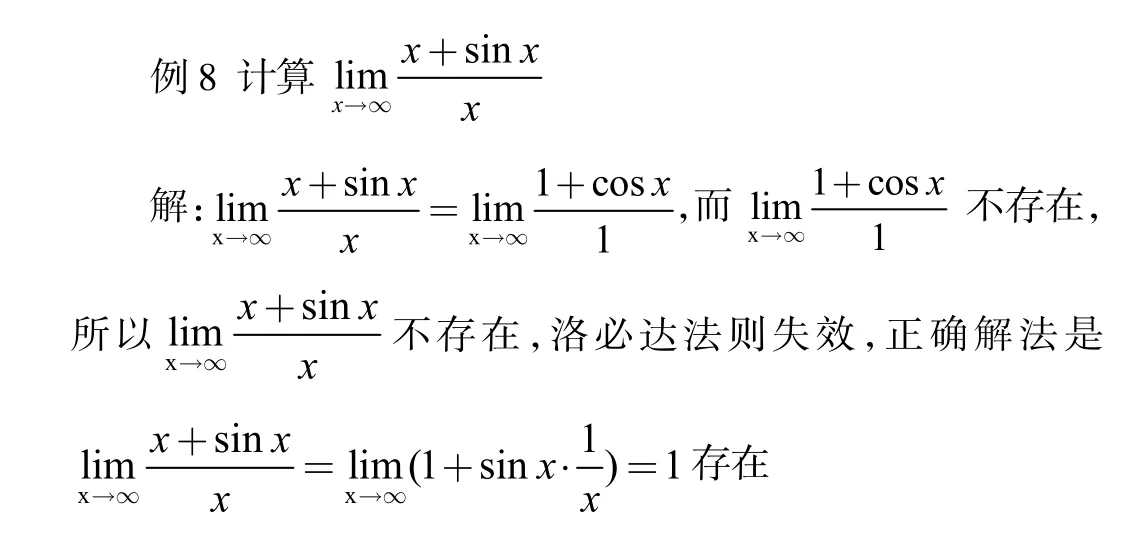
（二）使用洛必达法则后，函数出现循环，而无法求出极限，也就是不符合法则的条件（3）

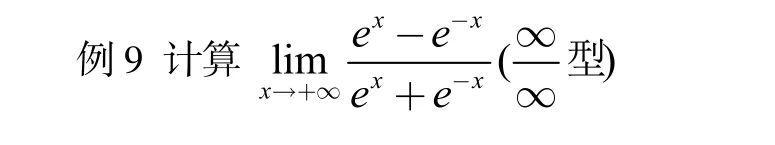
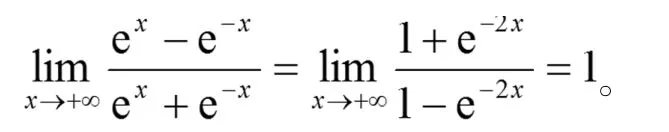
（三）使用洛必达法则后，函数越来越复杂，无法简单判断出函数是否存在极限，也就是不符合法则的条件（3）

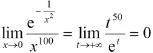
（四）求导后有零点，也就是不满足条件

例如

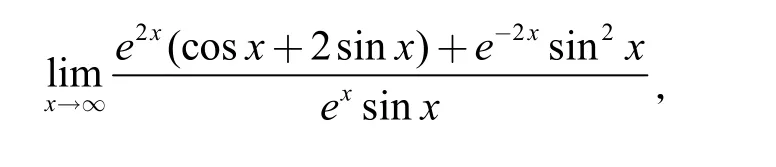
综合来看，我们在教学中既要向学生阐述清楚洛必达法则的巧妙和方便之处，也要向学生讲明白在使用洛必达法则解题过程中，可能会遇到的一些常见误区和盲点，为学生培养好的解题习惯，以减少在用洛必达法则解题过程中可能出现的失误。

［1］同济大学数学系.高等数学［M］.6版.北京：高等教育出版社，2007.

［2］华东师范大学数学系.数学分析［M］.3版.北京：高等教育出版社，2001.

［3］王世杰.浅析洛必达法则的应用［J］.山西煤炭管理干部学院学报，2007，20（4）：61-62.

［4］吴瑞玲.应用洛必达法则求极限时需注意的问题［J］.邢台职业技术学院学报，2013（1）：60-62.

［5］何少芳.用洛必达法则求未定式极限小结［J］.内江科技，2012（10）：169-171.

Combined with the teaching practice，this paper analyzes L' Hospital's Rule and its application in solving indeterminate form limit.It also analyzes the situation in which L' Hospital's Rule fails to solve the functional limit.

L' Hopital's rule；indeterminate form；limit

O13

A

2096-000X（2016）20-0089-02

张蕾（1984，06-），性别：女，民族：汉，籍贯：山东省齐河县，单位：山东职业学院，职称：助教，学历：研究生，研究方向：高等数学教学与研究。