离散系统倍周期分岔控制

韩　芩

(1.武昌工学院 机械工程学院,湖北 武汉 430065;2.华中科技大学 机械科学与工程学院,湖北 武汉 430074)



离散系统倍周期分岔控制

韩芩1,2

(1.武昌工学院 机械工程学院,湖北 武汉 430065;2.华中科技大学 机械科学与工程学院,湖北 武汉 430074)

通过研究一维离散系统的分岔特性和发生混沌的原因，设计了线性和非线性两种类型的控制器，并进行倍周期分岔控制，选取不同的控制器增益，使系统的倍周期分岔得到了延迟或者提前，显示了系统复杂的非线性动力特性，实践中可以选择不同的控制器增益和类型，实现预期的控制目标。

离散系统；倍周期分岔；分岔控制；控制器

1　引言

分岔是自然界一种基本的非线性自然现象，理论上，由于非线性动力学系统的运动状态失稳而发生分岔，以至于出现混沌是极其普遍的现象。随着非线性理论的发展，逐渐对分岔以及混沌都有了更加深入的了解。分岔研究成果应用于许多领域，如生物工程[1-3]、机械工程[4]等方面。

分岔控制作为分岔研究的重要内容之一，越来越得到重视，形成了一个新的控制理论方向。分岔控制的主要任务是对某一具体的系统设计一个控制器来改变其非线性特性，从而获得需要的动力学行为，实现预期的控制目标。分岔控制的主要方式[5-7]：将分岔的形状和类型进行修改；使系统的分岔解趋于稳定；产生新的分岔或使分岔的出现延迟；使系统极限环幅值或频率得到控制；控制系统的动力学不稳定解所在区域缩小；通过系统的分岔混沌特性实现分岔控制达到控制混沌的目的等等。

本文主要是针对于离散系统，分析了系统的非线性分岔特性，出现混沌的原因；并设计不同类型的控制器进行分岔控制，出现分岔点延迟或者提前，实现了控制混沌的目的。

一维离散系统为：

xn+1=λxn-xn2.

(1)

其中λ 是非负数常实数，x∈R。由于离散系统具有平方项，具有复杂的动力学模型。

2　分岔特性

根据不动点的定义，可得系统式(1)不动点

其迭代函数为 f(x)=λx-x2，这是一个典型的倍周期分岔系统。当λ由3过渡到4时，系统发生分岔，通过倍周期分岔产生混沌如图1所示。

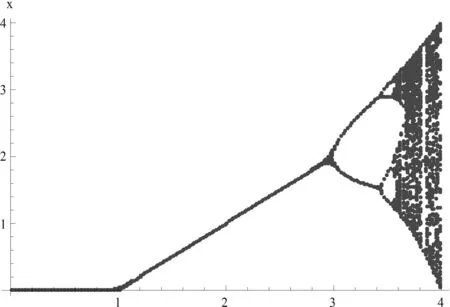
图1　一维离散系统分岔图

当1<λ<3时，除了2个不动点(1-周期点)外，还存在两个2-周期点。由

f2(x)= -x4+2 λx3-λx2-λ2x2+λ2x.

(2)

得：

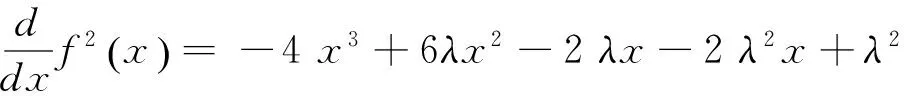
(3)

将不动点x*=λ-1代入(3)得：

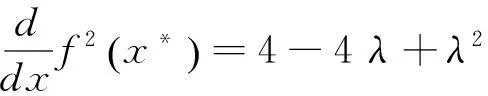
(4)

由f2(x)= x可得2-周期点，

当λ<3时，系统只有不动点；当λ=3时，

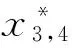
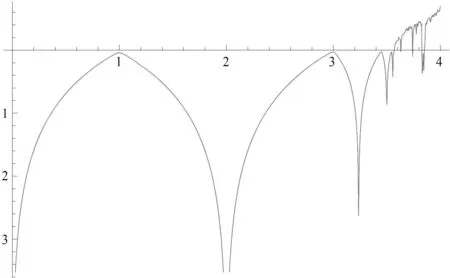
图2　系统Lyapunov指数谱

3　分岔控制

分岔控制是对原系统设计一个控制器，改变原系统的分岔特性。一般对于受控系统，其在不动点x*处的Jacobi矩阵为：

(5)

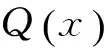
3.1线性控制

xn+1=λxn-xn2+k1+k2x.

(6)

通过取得不同的 k1、k2值得到系统受控的分岔情况如图3(a)、(b)、(c)、(d)所示。

(a)k1=-0.3,k2=0

(b) k1=0,k2=-0.9

(c)k1=-0.3,k2=-0.9

(d) k1=0.2,k2=0.9

k1=-0.3,k2=0时，受控系统式(5)的控制器退化为常数，系统倍周期分岔延迟,发生第一次倍周期分岔出现在[3.2,3.3]，第二次倍周期分岔出现在[3.6,3.7], 在[0,4]之间系统出现混沌；

k1=0,k2=-0.9时，受控系统式(5)的倍周期分岔延迟很明显,第一次倍周期分岔出现在[3.8，4]，在[0,4]没有第二次倍周期分岔，系统没有混沌现象；

k1=-0.3,k2=-0.9时，受控系统式(5)在[0,4]中的没有发生倍周期分岔，混沌现象消失；

k1=0.2,k2=0.9时，受控参数k1，k2取为正实数，系统式(2)的倍周期分岔反而提前,发生第一次倍周期分岔出现在[1.8，1.8]，第二次倍周期分岔出现在[2.3,2.4],系统出现混沌是在[2.8,2.9]之间。

从图3中看出，受控参数k1，k2为正实数时，受控系统会出现提前发生分岔的情况，相应的会提前进入混沌；取值为非正实数时，受控系统分岔延迟，进入混沌状态也得到相应的延迟或者消失。其中，k1的微小变化可以引起系统大幅度的延迟分岔的发生，即在控制器中起着粗调的作用。

3.2非线性控制

xn+1=λxn-xn2+k1x+k2x3.

(7)

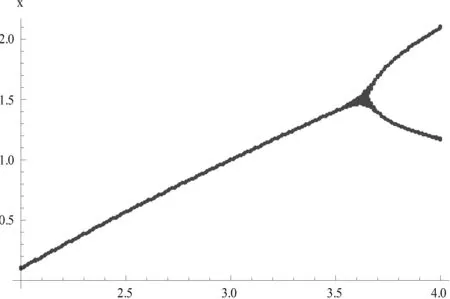
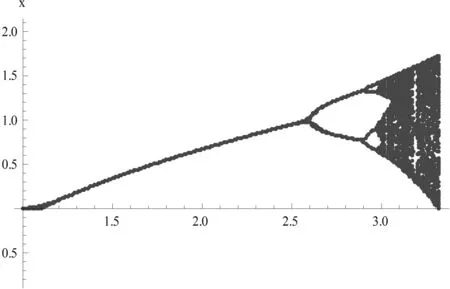
通过取得不同的 k1、k2值得到系统受控的分岔情况如图4(a)、(b)、(c)、(d)所示。

(a) k1=0,k2=-0.5

(b) k1=-0.1,k2=-0.9

(c) k1=-0.2,k2=-0.9

(d)k1=-0.1,k2=-0.1

k1=0,k2=-0.5时，受控系统式(6)的倍周期分岔不仅没有得到延迟,反而发生第一次倍周期分岔提前，出现在[2.4，2.5]，第二次倍周期分岔出现在[2.8,2.9],在[2.9,3]之间系统出现混沌；

k1=-0.1,k2=-0.9时，受控系统式(6)的倍周期分岔的得到延迟，第一次倍周期分岔出现在[3.6,3.7]。在[0.4]之间只发生一次倍周期分岔出现，第二次倍周期分岔、混沌等特性都消失；

k1=-0.2,k2=-0.9时，受控系统式(6)分岔延迟，发生第一次倍周期分岔出现在[3.5，3.6]，第二次倍周期分岔出现在[3.8,3.9],在[0,4]之间系统出现混沌；

k1=-0.1,k2=-0.1时，受控系统式(6)分岔也提前了，发生第一次倍周期分岔出现在[2.5，2.6]，第二次倍周期分岔出现在[2.9,3],系统进入混沌也相应提前，在[0,3.3]之间就出现混沌。

从图4中看出，控制器为单一的立方非线性控制器时，系统的分岔不仅得不到延迟，反而是提前的，也相应的提前进入混沌状态。当k1从0变为-1时，受控系统的分岔特性大幅得到延时，但是再设置为-1.2时，受控系统的分岔变化就不明显，说明非线性控制器中k1不再起着粗调的作用。作为非正实数k2决定着系统分岔的提前或延时，随着k2值逐渐增加，系统的分岔逐渐由延迟变为提前。因此，选择好k1、k2值，可以实现控制目标。

4　结束语

笔者分析了离散系统的分岔特性，详细探讨的系统在参数λ的变化下，产生倍周期分岔，由1-周期过渡到2-周期，再到4-周期，最后出现混沌。并以此设计了线性控制器和非线性控制器，有效的控制系统的倍周期分岔，使系统的混沌行为得到控制。

[1]Xue Zhang,Qingling Zhang,Victor Sreeram. Bifurcation analysis and control of a discrete harvested prey-predator system with Beddington-DeAngelis functional response[J].Journal of the Franklin Institute,2010, 347 (7): 1076-1096.

[2]Dongmei Xiao, Wenxia Li , Maoan Han.Dynamics in ratio-dependent predator-prey model with predator harvesting[J], Journal of Mathematical Analysis and Applications,2006,324(1):14-29.

[3]Kumar S,Srivastava S K, Chingakham P. Hopf bifurcation and stability analysis in a harvested one- predator-two-prey model[J], Applied Mathematics and Computation，2002,129(1):107-118.

[4]Jorge Moiola,Alfredo Desages,Jose Romagnoli..Degenerate. Hopf bifurcations via feedback system theory: higher order harmonic balance[J]. Chemical Engineering Science, 1991, 46 (5-6):1475-1490.

[5]Ji J C, Leung A Y T. Resonances of a non-linear s.d.o.f. system with two time-delays in linear feedback contro1[J]. Journal of Sound and Vibration, 2002, 253(5):985-1000.

[6]唐驾时, 欧阳克俭. Logistic 模型的倍周期分叉控制[J].物理学报，2006，55(9)：4437-4441.

[7]刘丁，钱富才,任海鹏，等.离散混沌系统的最小能量控制[J].物理学报，2004，53(7):2074-2078.

The periodic bifurcation control of the discrete system

HANQin1,2

(1.College of Mechanical Engineering,Wuchang Institute of Technology,Wuhan 430065,China; 2.School of Mechanical Science and Engineering,Huazhong University of Science and Technology,Wuhan 430074,China)

Research the characteristic of the bifurcation,and the process of chaos to the one-dimensional discrete system. According to the characteristics,design two types controllers of the linear and non-linear.The periodic bifurcation control,and the choice of the different controller gains,make the system delayed or advanced ,which displays the complex non-linear dynamic characteristics.In practice , the different controller gains and types can be chosen to achieve the control objectives.

discrete system;periodic bifurcation;bifurcation control;controllers.

2016-04-19

韩芩(1984-),女,助教,工程硕士,E-mail: duoduo0310@sina.com.

湖北省绿色风机协同创新中心项目(2015XTJY01).

2095-7386(2016)03-0064-04

10.3969/j.issn.2095-7386.2016.03.012

TP 273

A