钢-UHPC轻型组合梁桥面板受弯性能有限元分析

孔令方，邵旭东,2，刘　榕

(1.湖南大学　土木工程学院，湖南　长沙　410082；2.湖南大学　风工程与桥梁工程湖南省重点实验室，湖南　长沙　410082；3.湖南省交通规划勘察设计院，湖南　长沙　410008)



钢-UHPC轻型组合梁桥面板受弯性能有限元分析

孔令方1，邵旭东1,2，刘榕3

(1.湖南大学土木工程学院，湖南长沙410082；2.湖南大学风工程与桥梁工程湖南省重点实验室，湖南长沙410082；3.湖南省交通规划勘察设计院，湖南长沙410008)

为降低常规钢-混凝土组合主梁结构的自重,解决其混凝土桥面板易开裂的问题，提出了钢-UHPC轻型组合梁结构方案，该结构方案能明显降低结构自重。为得到新型钢-UHPC轻型组合梁结构桥面板的受力状况，以在建实桥应用工程胜天大桥为工程背景，分别采用应力叠加法、全桥精细有限元法和混合有限元法，对其桥面板受力最不利位置的纵桥向拉、压应力进行了计算分析。结果表明：混合有限元法与全桥精细有限元法计算结果相差在4%以内，二者结果较接近；应力叠加法相比全桥精细有限元法计算结果差值为1.58～3.80 MPa，相差在12%以上，结果偏保守。计算结果与试验结果对比表明，UHPC桥面板纵桥向最大设计拉应力小于UHPC最大裂缝宽度为0.05 mm时的实测名义拉应力，纵桥向压应力远小于UHPC抗压强度，能够满足在最不利加载工况下的设计要求。

桥梁工程；钢-UHPC轻型组合梁；有限元分析；UHPC层应力；应力叠加法；全桥精细有限元法；混合有限元法

U441+.5

0　引言

相对于纯钢桥，常规钢-混凝土组合结构桥梁可以有效降低造价，提高结构刚度，减小结构在活荷载下的挠度[1]。但常规组合梁混凝土板厚度较大，一般大于28 cm，这增大了桥梁的自重，使常规组合梁难以适用于特大跨径的桥梁结构[2]。此外，温度、混凝土收缩徐变效应及反复车辆荷载作用下，常规钢-混凝土组合结构桥梁极易开裂，且在预压应力较小的跨中区段该类裂缝尤为明显，其原因为普通混凝土材料具有抗拉应变小、抗拉强度低以及收缩徐变效应明显的特性，同时组合梁桥面板和下部钢梁采用刚性连接约束，桥面板自由变形能力差，致使混凝土桥面板在外部荷载及效应作用下极易开裂[3]，并会进一步导致主梁结构刚度下降、内部钢筋和下部钢结构的锈蚀等问题，影响桥梁结构的耐久性和安全性。可见，这些问题的根本原因均与常规钢-混凝土组合主梁结构及材料密切相关。

超高性能混凝土(Ultra-high performance concrete,UHPC)是一种新型纤维增强水泥基复合材料，具有超高强度、超高韧性、良好耐久性和低磨耗性[4-5]的特征。为充分利用UHPC的优良性能，将其与钢梁组合，可以得到结构性能更加高效和优异的组合梁结构。国内学者将UHPC与正交异性钢板组合，形成“轻型组合桥面板结构”，并对其静力性能和疲劳性能进行了大量研究[2,6]。国外学者研究了配筋UHPC板[7]及配筋UHPC与普通混凝土构成的新型组合梁的受弯性能[8]。

为降低常规钢-混凝土组合主梁结构的自重，同时解决其混凝土桥面板易开裂的问题，作者所在团队提出将UHPC桥面板与钢梁通过抗剪连接件连接成整体共同受力，形成“钢-UHPC轻型组合梁结构”。为更充分利用UHPC的优良性能，进一步降低组合梁自重，UHPC桥面板采用板底纵横加肋的华夫板形式。

本文以在建实桥应用工程胜天大桥为背景，提出了钢-UHPC轻型组合梁斜拉桥设计方案，由于钢-UHPC轻型组合梁结构采用华夫型UHPC桥面板，其顶板较薄，为获得汽车荷载作用下桥面板的局部应力，检验桥面板是否开裂，分别采用应力叠加法、全桥精细有限元法和混合有限元法对UHPC桥面板的受力进行分析。

1　工程概况及轻型组合梁结构

在建南益高速胜天大桥为三跨连续组合梁、双塔双索面斜拉桥，桥跨布置为(181.95+450+181.95)m，全长813.9 m，见图1。主梁采用PK型分离双箱组合梁形式，见图2，组合梁全宽29.3 m，梁高3.5 m。标准梁段横隔板间距3.5 m，加密梁段调整为2.25 m，无拉索处横隔板厚12 mm，拉索处厚16 mm。斜拉索标准索距为10.5 m，加密区为4.5 m，每个索塔两侧各布置20对，全桥共80对斜拉索。

该桥索塔处与过渡墩处均设置竖向支座。桥面为双向六车道，设计荷载为公路-I级。

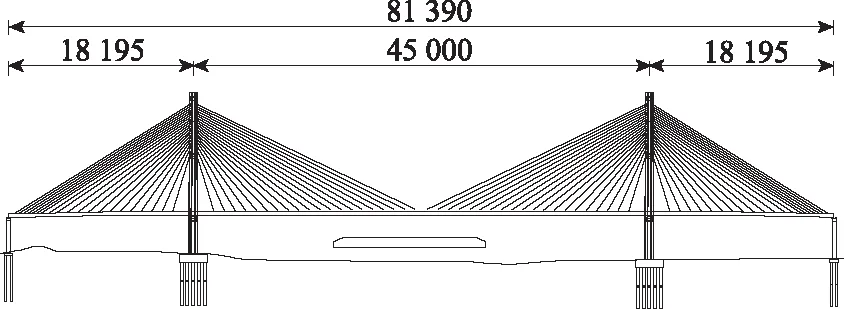
图1　胜天大桥纵断面图(单位：cm)Fig.1　Longitudinal section of shengtian Bridge (unit:cm)

本桥在优化前组合梁桥面板采用普通混凝土，平均厚度为31 cm；经优化，桥面板现采用UHPC华夫板形式，见图3，桥面平板厚8 cm，纵横肋高14 cm，总厚22 cm；纵肋下缘宽18 cm，上缘宽20 cm，标准间距0.7 m；两横隔板间布置2个横肋，横肋下缘宽10 cm，上缘宽12 cm，间距1.1 m。UHPC华夫板等效厚度(面积相等)约为14 cm，较常规钢-混凝土组合梁桥面板，其自重将明显降低。

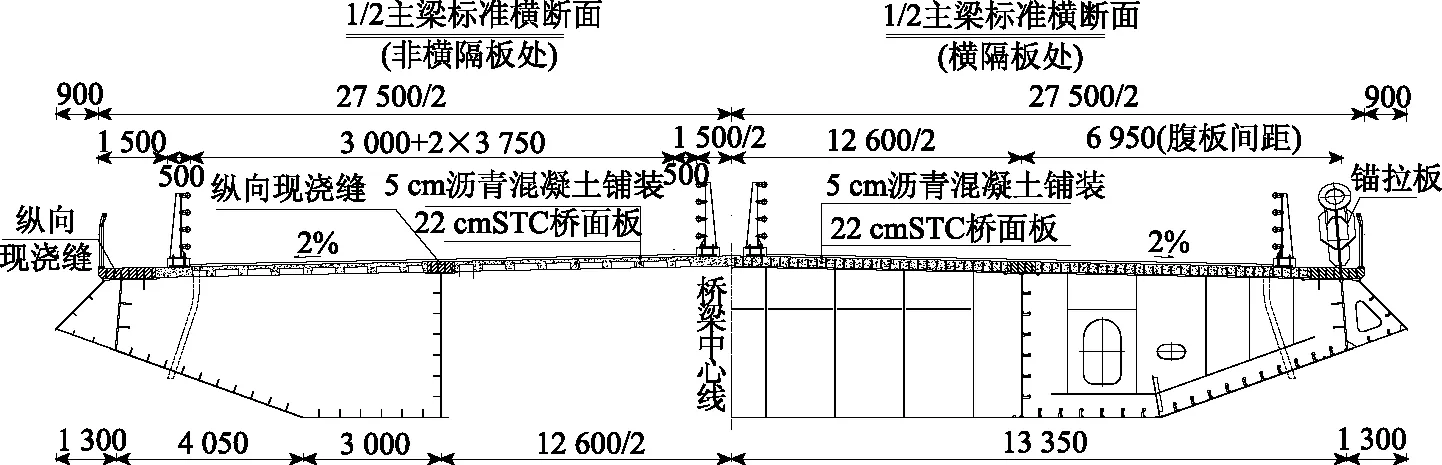
图2　胜天大桥横断面图(单位：mm)Fig.2　Cross-section of Shengtian Bridge (unit: mm)

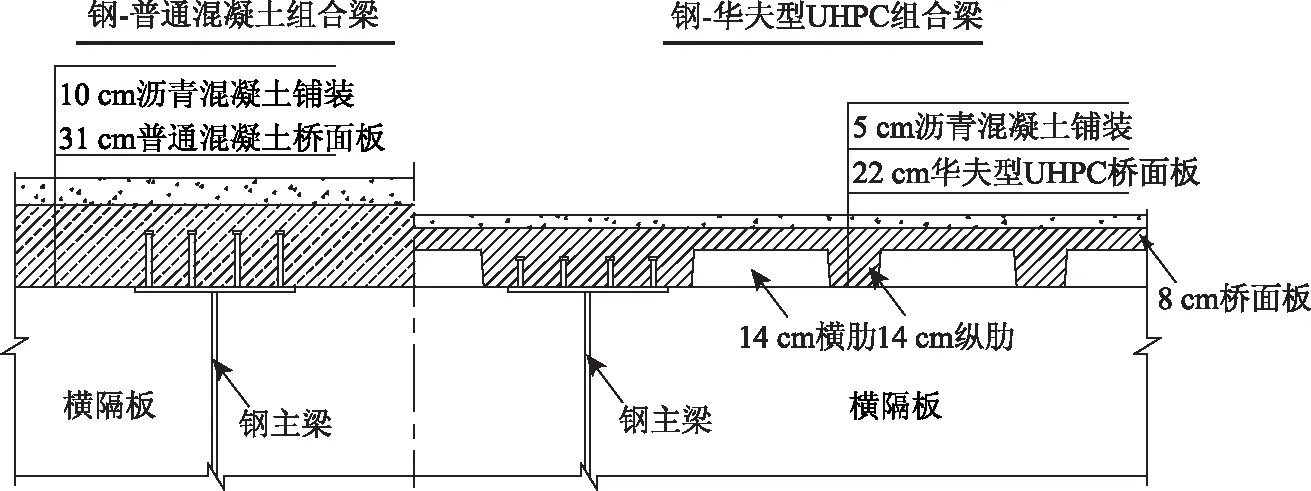
图3　两种不同的组合梁横断面图Fig.3　Cross-section of 2 kinds of composite girder

依据目前市场建筑材料价格行情，对两种组合梁的桥面结构造价进行对比，如表1所示。

由表1可知，钢-UHPC轻型组合梁桥面结构在初始造价方面较常规钢-混凝土组合梁桥面结构昂贵，但纵观桥梁全寿命周期，由于UHPC耐久性能远优于普通混凝土，因此，其全寿命造价与常规钢-混凝土组合梁桥面结构相当。此外，由于钢-UHPC轻型组合梁自重明显降低，斜拉索、桥塔和基础的工程量均显著减少，从而可降低全桥的总造价。

表1　不同桥面结构造价对比表Tab.1　Comparison of costs of different deck structures

2　有限元计算

对桥面板进行受力分析时，通常采用先分体系计算应力，再近似叠加求得总应力的方法，即传统应力叠加法[9]。传统应力叠加法是根据假设人为的将主梁划分为3个基本结构体系，即主梁体系、桥面体系和盖板体系，计算虽然比较便捷，但结果一般偏于保守，因而存在一定的局限性[10]。全桥精细有限元法采用实体单元或壳单元模拟主梁，可以较真实地反映全桥受力情况。但由于计算机软硬件的限制，且建立全桥精细模型过程复杂，这种方法不被普遍采用。混合有限元法对结构不同部位分别建立不同尺度的有限元模型，再通过边界约束的匹配将不同尺度的结构模型联系在一起，从而可以在不同尺度模型上进行不同精细程度的单元网格划分，以满足不同分析精度的要求[11]。苏庆田、吴永昌等[12]采用混合有限元方法，用壳单元模拟关注部位的钢箱梁，用梁单元模拟其他部位的钢箱梁，计算结果表明该方法能真实反映结构的受力情况。孙正华、李兆霞等[13]针对大型结构，以健康监测和损伤评估为目标进行了有限元分析，结果表明可以采用结构行为一致混合模拟方法以同时兼顾结构整体响应和局部细节响应模拟的需求。

该钢-UHPC轻型组合梁结构桥面板以纵桥向受力为主，本文取背景斜拉桥受力最不利梁段桥面板为研究对象，分别采用传统应力叠加法、全桥精细有限元法和混合有限元法计算其纵桥向最大应力，并对计算结果进行对比分析。

2.1传统应力叠加法2.1.1第一体系应力计算

采用Midas有限元软件建立单主梁整桥有限元模型，见图4，主梁采用与组合梁具有相同截面面积(换算截面面积)、抗弯惯性矩和抗扭刚度的梁单元模拟，索塔采用梁单元模拟，斜拉索采用杆单元模拟。

图4　整体有限元模型Fig.4　Integrated finite element model

整体有限元模型计算荷载为：结构自重、桥面铺装、边跨压重及汽车荷载。其中，UHPC重度28 kN/m3，面铺装简化为作用于主梁上的线荷载，大小为36.4 kN/m，边跨压重在梁段最大处为 880 kN/m，全桥共计压重3 929 t；汽车荷载采用车道荷载，集中力大小为360 kN，均布荷载为10.5 kN/m，考虑横向多车道折减、纵向折减和0.05倍冲击系数[14]。

由整体有限元模型计算结果得到桥面板纵桥向拉、压应力最不利位置分别位于如图4所示跨中和近桥塔处梁段。分析主梁结构可知，桥面板下缘纵桥向最大拉应力的纵向位置位于两横隔板中间处；上缘纵桥向最大拉应力的纵向位置位于横隔板处，在正弯矩作用时两横隔板中间处的桥面板上缘取得纵桥向最大压应力。因此本文选取这两个梁段范围内桥面板，对其纵桥向最不利拉、压应力进行计算分析。其中，最不利拉应力包括正、负弯矩下的最大应力，分别位于桥面板a截面处下缘和b截面处上缘；而最不利压应力位于桥面板c截面处上缘。

提取整体有限元模型计算结果中最不利截面处的内力(弯矩、轴力)，在考虑组合梁剪力滞效应的基础上，根据初等梁理论求解桥面板纵桥向应力可得：跨中梁段a截面处桥面板下缘纵桥向拉应力为2.53 MPa，b截面处桥面板上缘纵桥向拉应力为2.88 MPa；近桥塔梁段c截面处桥面板上缘纵桥向压应力为-13.72 MPa。以上求解正应力即为相应的第一基本结构体系下桥面板正应力[15]。

2.1.2节段局部应力计算

(1)模型建立及边界条件

取最不利位置处10跨横隔板间距梁段，采用ANSYS有限元软件建立节段有限元模型，见图5。其中，UHPC桥面板(弹性模量为4.26×104MPa，泊松比为0.2)采用SOLID45实体单元模拟，钢板(弹性模量为2.1×105MPa，泊松比为0.3)采用SHELL63壳单元模拟。

由于荷载作用下节段的整体位移已在整体有限元计算中体现，因而节段有限元模型的边界条件为：在各横隔板与边腹板交界处，约束模型竖向平动自由度；并约束模型的刚体位移。如此计算模型得到的结果仅为局部应力。

图5　节段有限元模型Fig.5　Segmental finite element model

(2)有限元模型最不利位置确定及荷载施加

为进一步确定以上桥面板纵桥向应力在横桥向断面上的最不利位置，计算得到各纵桥向应力横向影响线的包络线，见图6。由包络线可得纵桥向应力在横桥向断面上的最不利位置为图示A点、B点、C点，进而根据该点位处纵桥向应力的横向影响线，确定车辆横向加载位置。再分别计算A点、B点、C点纵桥向应力的纵向影响线，见图7～图9，据此确定车辆纵向加载位置。

图6　横向影响线的包络线及横向最不利位置Fig.6　Envelope of horizontal influence line and transverse most unfavorable position

节段有限元模型的计算荷载为：结构自重、桥面铺装和汽车荷载，模型不考虑斜拉桥整体受力中主梁轴力、剪力和弯矩的影响[16]。其中，汽车荷载采用车辆荷载，为总重550 kN的标准车，并计入0.3倍冲击系数[14]。分别按A，B，C点的横、纵向影响线布置车辆位置，由A，B，C点的横向影响线图形可知，横向并排布置两辆车即可。如图7～图9所示，车辆横向位置可分为车轮荷载作用于横向影响线峰值处和相对峰值位置对称布置两种；车辆纵向位置可分为车辆单轴荷载作用于纵向影响线峰值处和车辆后轴荷载相对峰值位置对称布置两种。计算得到各工况下的应力峰值如表2所示。

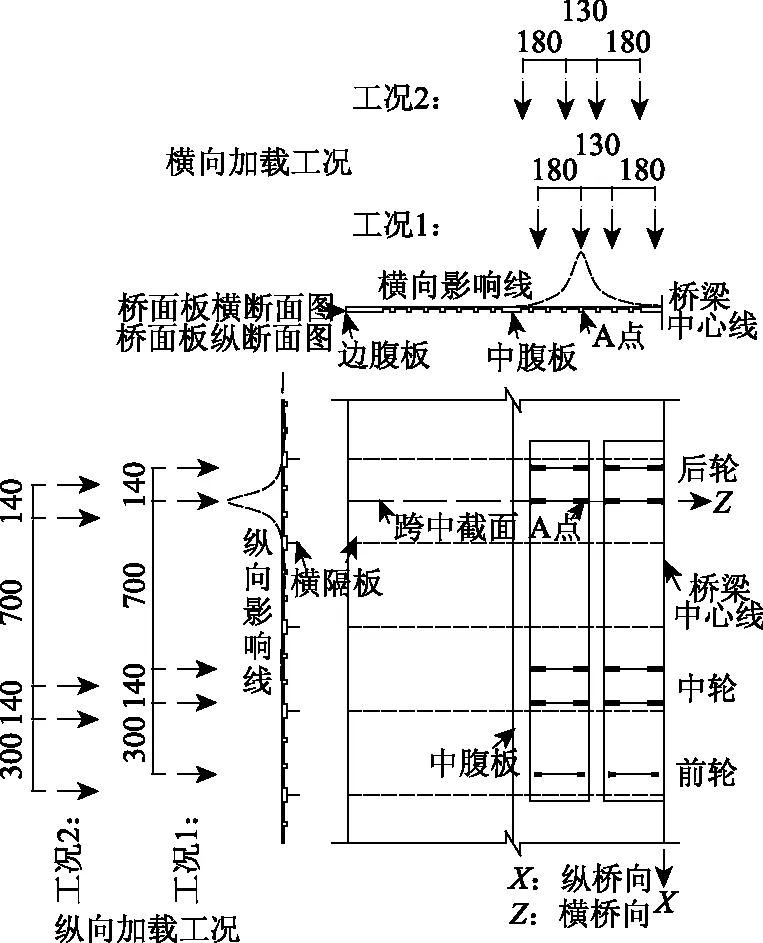
图7　桥面板下缘纵桥向拉应力影响线(单位：cm)Fig.7　Influence lines of longitudinal tensile stress on lower edge of bridge deck(unit: cm)

图8　桥面板上缘纵桥向拉应力影响线(单位：cm)Fig.8　Influence lines of longitudinal tensile stress on upper edge of bridge deck(unit: cm)

图9　桥面板上缘纵桥向压应力影响线(单位：cm)Fig.9　Influence lines of longitudinal compressive stress on upper edge of bridge deck(unit:cm)表2　各工况计算结果表(单位：MPa)Tab.2　Calculation result of different working conditions (unit:MPa)

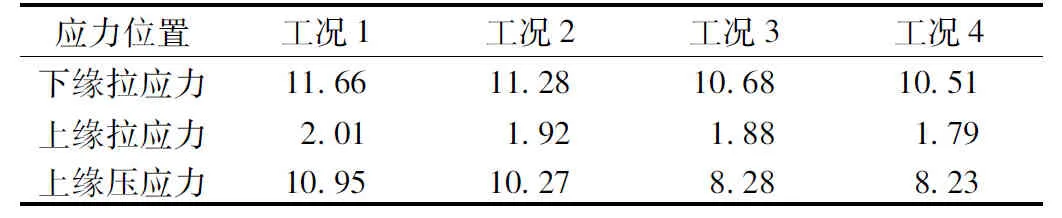
应力位置工况1工况2工况3工况4下缘拉应力11.6611.2810.6810.51上缘拉应力2.011.921.881.79上缘压应力10.9510.278.288.23

由表2可知，当车轮在纵横向均作用在影响线峰值处时，该工况下的应力最大，说明由于桥面板较薄，车辆荷载的局部效应较明显。

2.2全桥精细有限元法2.2.1有限元模型建立及边界条件

采用ANSYS有限元软件建立全桥精细有限元模型，见图10。UHPC桥面板采用SOLID45实体单元模拟，钢板采用SHELL63壳单元模拟，普通混凝土索塔采用BEAM189梁单元模拟，斜拉索采用LINK10杆单元模拟，斜拉索采用Ernst公式考虑垂度效应。

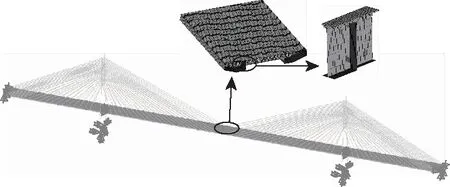
图10　全桥精细有限元模型Fig.10　Full-scale fine finite element method

模型边界条件为：塔底处固结；耦合主梁与索塔下横梁的竖向平动自由度；在主梁两端处，约束主梁竖向平动自由度，并在一端约束主梁纵桥向平动自由度；为避免斜拉索在主梁锚固处的应力集中现象，耦合锚拉板范围内有限元模型节点的竖向平动自由度。

为得到更精确的桥面板应力值，本文采用子模型技术，在保证子模型边界对最不利梁段关注位置影响最小的前提下，将最不利位置处10个横隔板间距的局部节段从全桥有限元模型中提取出来。子模型所采用单元与全桥精细有限元模型相同。

子模型的边界条件为：将全桥精细有限元模型计算得到的位移场施加在子模型中的边界节点上[17-18]；子模型区域内不建立斜拉索的单元模型，而是由全桥精细有限元模型计算得到的相应索力代替。

2.2.2荷载施加

全桥精细有限元模型计算荷载为：结构自重、桥面铺装、边跨压重及汽车荷载。

其中桥面铺装和边跨压重按面荷载施加在相应位置。为更真实地模拟汽车荷载作用，同时考虑汽车荷载的总体荷载效应和局部荷载效应，汽车荷载同时采用车道荷载和车辆荷载。最不利梁段影响线峰值区域的汽车荷载布置，如图11(b)所示，车辆荷载采用3辆重550 kN的标准车，按最不利位置处的纵向和横向影响线布置车辆位置；为确定车道荷载的纵向加载位置，由2.1.1节中的整桥有限元模型计算得到最不利截面的全主梁弯矩纵向影响线，用于布置车道荷载，见图12，其大小和纵向布载位置与整桥有限元模型相应位置处的车道荷载相同。为保证全桥精细有限元模型汽车荷载与整桥有限元模型大小一致，则最不利梁段影响线峰值区域的荷载须相等。为此，经计算在车辆荷载两端纵向净距7.16 m内不施加车道荷载，如此也可避免车辆荷载与车道荷载的局部效应叠加[14]。两种有限元模型的荷载对比如表3所示。

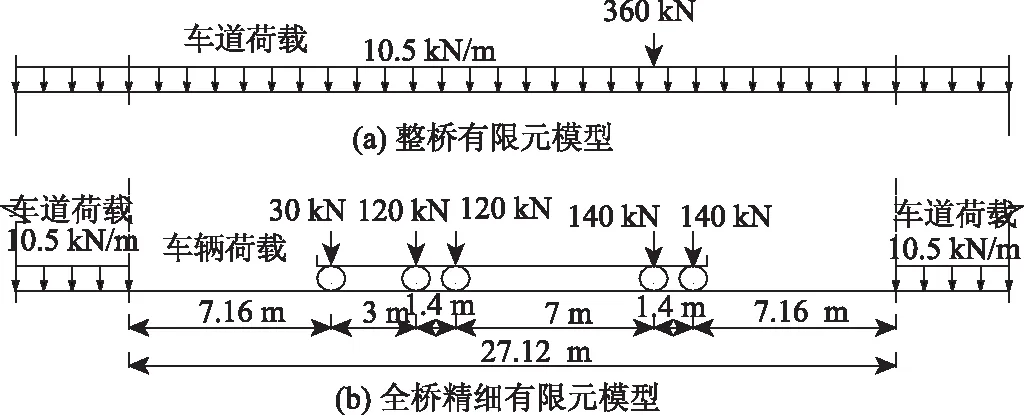
图11　影响线峰值区域的荷载Fig.11　load at peak part of influence line

图13　混合有限元模型Fig.13　Mixed finite element model

图12　最不利位置弯矩纵向影响线Fig.12　Longitudinal influence lines of bending moment at most unfavorable girder position

2.3混合有限元法

为与全桥精细有限元模型相校核及对比，采用ANSYS有限元软件建立混合有限元模型，见图13。为减小边界条件对关注区域的影响，分别在主跨跨中和近桥塔处取10个横隔板间距建立节段精细有限元模型，其余部分主梁采用BEAM4梁单元模拟；混合有限元模型的索塔、斜拉索模拟与全桥精细有限元模型相同；梁单元主梁与斜拉索之间通过刚臂单元连接，刚臂采用BEAM4梁单元模拟；主梁的节段精细有限元模型与梁单元模型之间采用CERIG命令耦合[17]，使交界面上满足平截面假定。

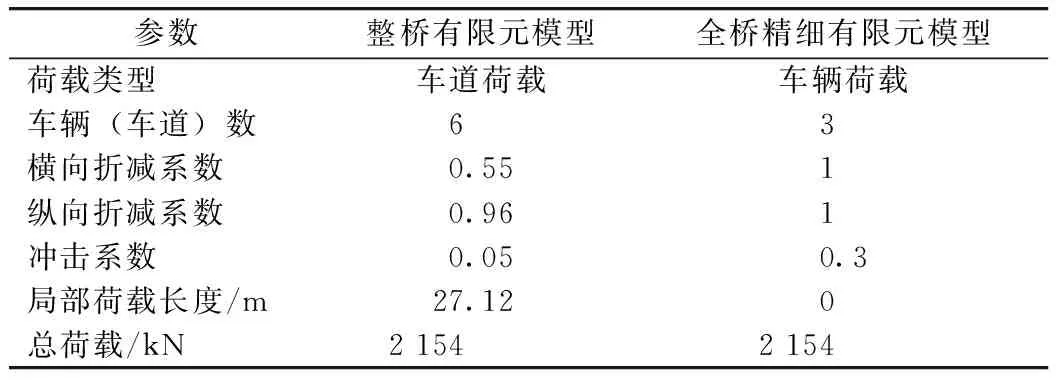
表3　影响线峰值区域有限元模型荷载对比Tab.3　Load comparison of finite element models at influence line peak area

混合有限元模型的边界条件、最不利位置确定方法和荷载加载方式均与全桥精细有限元模型相同，其中位于梁单元主梁处的荷载需简化为线荷载，且大小与全桥精细有限元模型一致。

3　模型单元数量及有限元计算结果对比分析

3种有限元方法各模型单元数量统计如表4所示。

表4　各有限元模型单元数量表Tab.4　Element number of finite element models

由表4可知，全桥精细有限元法建立模型需要超过104万个实体单元和82万个壳单元，有885万个有效自由度，且仍需要建立子模型模拟局部细节特性，需要耗费大量机时；混合有限元模型与应力叠加法局部有限元模型单元数量相当，需要约57万个实体单元和18.8万个壳单元，有效自由度数也相当，均有337万个有效自由度。采用3种有限元方法计算得到桥面板纵桥向拉、压应力峰值结果如表5所示。

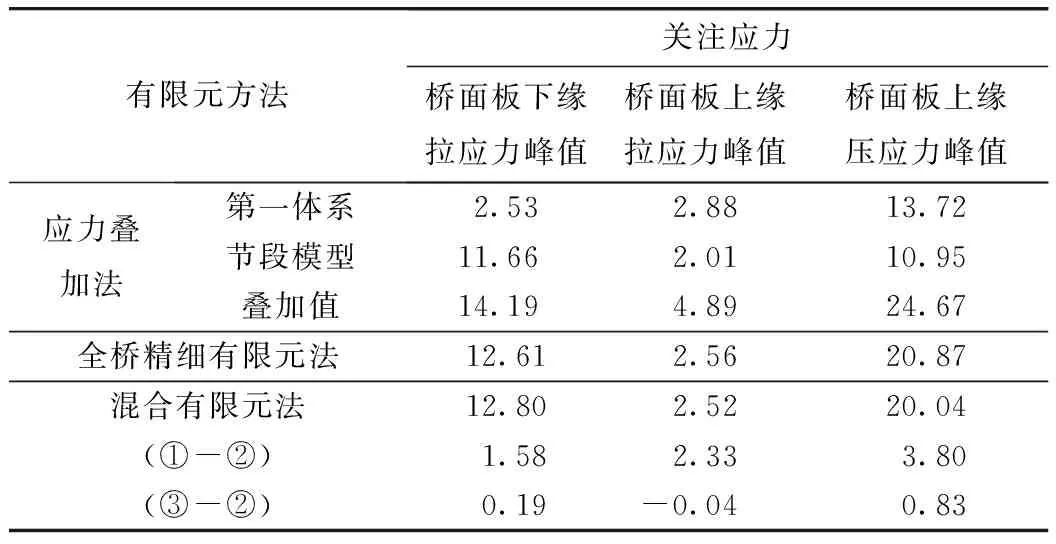
表5　桥面板应力计算结果(单位：MPa)Tab.5　Calculation result of stress of bridge deck (unit:MPa)

注：①、②、③分别代表应力叠加法、全桥精细有限元法、混合有限元法。计算3个应力峰值的百分比，①/②-1=12.56%，91.02%，18.21%，③/②-1=1.51%，-1.56%，-3.98%。

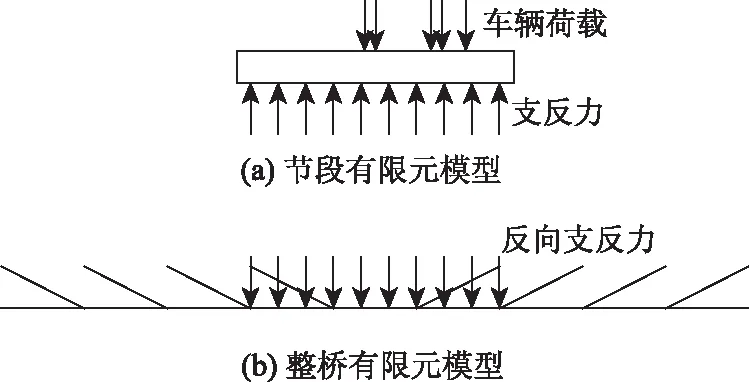
图14　应力叠加法真实荷载Fig.14　Real load for stress superposition method

由表5可知，对比全桥精细有限元法计算结果：采用混合有限元法计算的桥面板上下缘应力，偏差均在4%以内，计算结果基本一致，表明混合有限元法与全桥精细有限元法计算结果比较接近，也证明了两种方法计算结果的准确性；采用应力叠加法计算桥面板下缘拉应力峰值比全桥精细有限元法结果大1.58 MPa，上缘拉应力峰值比全桥精细有限元法结果大2.33 MPa，上缘压应力峰值应力叠加法与全桥精细有限元法大3.80 MPa，偏差最小为12.56%，二者计算结果相差较大，偏于保守。如图14所示：在车辆荷载作用下，节段有限元模型受到约束的支反力作用，因此整桥有限元模型中相应梁段的荷载应为此反向支反力，而传统应力叠加法中整桥有限元模型的荷载为车道荷载，此处荷载的差异是导致传统应力叠加法计算结果误差较大的主要原因。

UHPC试验梁在下缘各级名义拉应力作用下的裂缝宽度如表6[2]所示。

表6　裂缝宽度的试验结果Tab.6　Test result of crack width

由表6可知，当UHPC表面的最大裂缝宽度为0.05 mm时，其名义拉应力为19.36 MPa，而由表5可知3种有限元方法计算得到的桥面板拉应力峰值均小于该名义拉应力，此拉应力下的裂缝对UHPC的耐久性毫无影响[19]；UHPC的抗压强度达150 MPa 以上[20]，表5中桥面板压应力峰值远小于其抗压强度，表明在运营荷载下，华夫型UHPC桥面板处于线弹性受力状态，能够满足在上述最不利加载工况下的设计要求。

4　结论

通过上述研究，得到结论如下：

(1)钢-UHPC轻型组合梁结构能明显降低组合梁结构的自重，且其力学性能优越，耐久性好。

(2)混合有限元法与全桥精细有限元法计算结果基本一致，表明混合有限元法在同时考虑结构整体和局部细节特性的结构行为一致时的有效性，并且可以灵活地对重要分析部位进行细致分析，该方法能够真实模拟结构的实际受力状态。

(3)应力叠加法计算结果明显大于全桥精细有限元法，计算结果偏于保守。

(4)该钢-UHPC轻型组合梁结构能够满足胜天大桥桥面板对拉应力、压应力及抗裂安全性的工程要求，能够有效解决钢-混凝土组合梁桥面板易开裂的问题。

[1]聂建国, 陶慕轩, 吴丽丽,等. 钢-混凝土组合结构桥梁研究新进展[J]. 土木工程学报, 2012(6):110-122.

NIE Jian-guo, TAO Mu-xuan, WU Li-li，et al. Advances of Research on Steel-concrete Composite Bridges[J]. China Civil Engineering Journal, 2012(6):110-122.

[2]邵旭东,胡建华.钢-超高性能混凝土轻型组合桥梁结构[M]. 北京：人民交通出版社, 2015.

SHAO Xu-dong, HU Jian-hua. The Steel-UHPC Lightweight Composite Bridge Structures[M]. Beijing: China Communications Press, 2015.

[3]李辉.钢_混凝土组合梁斜拉桥病害及其影响分析[D].哈尔滨：哈尔滨工业大学,2008.

LI Hui. The Analysis of Disease and Its Effect on Cable Stayed Bridge with Composite Girder[D]. Harbin: Harbin Institute of Technology, 2008.

[4]GRAYBEAL B A. Structural Behavior of Ultra-High Performance Concrete Prestressed I-girders, FHWA-HRT-06-115 [R]. Washington, D. C.: Federal Highway Administration, 2006.

[5]GRAYBEALB A. Material Property Characterization of Ultra-high Performance Concrete, FHWA-HRT-06-103 [R]. Washington, D. C.: Federal Highway Administration, 2006.

[6]SHAO X D,YI D T,HUANG Z Y,et al. Basic Performance of the Composite Deck System Composed of Orthotropic Steel Deck and Ultrathin RPC Layer [J]. Journal of Bridge Engineering,2011，18(5):417-428.

[7]YANG Yu-guang, JOOST W, UIJL J D. Study on Bending Behavior of an UHPC Overlay on a Steel Orthotropic Deck[C]// Proceedings of 2nd International Symposium on Ultra High Performance Concrete. Kassel, Germany: Kassel University Press, 2008: 639-646.

[8]HABEL K, DENARIE E, BRUHWILER E. Experimental Investigation of Composite Ultra-high-performance Fiber-reinforced Concrete and Conventional Concrete Members[J]. ACI Structural Journal,2007,104(1): 93-101.

[9]兰枢灵.薄壁钢箱梁计算方法研究[D].西安：长安大学,2011.

LAN Shu-ling. Study on the Calculation Method of Thin-walled Steel Box Girder[D].Xi’an: Chang’an University, 2011.

[10]孔祥福, 周绪红, 狄谨,等. 钢箱梁斜拉桥正交异性桥面板的受力性能[J]. 长安大学学报：自然科学版, 2007, 27(3):52-56.

KONG Xiang-fu, ZHOU Xu-hong, DI Jin, et al. Orthotropic Deck Performance of Steel Box Girder Cable-stayed Bridge[J]. Journal of Chang’an University: Natural Science Edition, 2007, 27(3):52-56.

[11]孙正华,李兆霞, 陈鸿天. 大型土木结构的结构行为一致多尺度模拟——模拟方法与策略[J]. 计算力学学报, 2009, 26(6):886-892.

SUN Zheng-hua,LI Zhao-xia,CHEN Hong-tian. Concurrent Multi-scale Modeling of Structural Behavior for Response Analysis of Large Civil Infrastructure: Modeling Methodology and Strategy [J]. Chinese Journal of Computational Mechanics, 2009, 26(6):886-892.

[12]苏庆田, 吴冲, 董冰. 斜拉桥扁平钢箱梁的有限混合单元法分析[J]. 同济大学学报：自然科学版, 2005, 33(6):742-746.

SU Qing-tian, WU Chong, DONG Bing. Analysis of Flat Steel-box-girder of Cable-stayed Bridge by Finite Mixed Element Method [J]. Journal of Tongji University: Natural Science Edition, 2005, 33(6):742-746.

[13]孙正华, 李兆霞, 陈鸿天. 大跨斜拉桥结构行为一致多尺度有限元模拟[J].中国公路学报, 2009，22(5):68-74，117.

SUN Zheng-hua, LI Zhao-xia, CHEN Hong-tian. Concurrent Multi-scale Finite Element Modeling of Long-span Cable-stayed Bridge [J]. China Journal of Highway and Transport, 2009，22(5):68-74，117.

[14]JTG D60—2015, 公路桥涵设计通用规范[S].

JTG D60—2015, General Code for Design of Highway Bridges and Culverts [S].

[15]徐伟, 李智, 张肖宁. 子模型法在大跨径斜拉桥桥面结构分析中的应用[J]. 土木工程学报, 2004, 37(6):30-34.

XU Wei, LI Zhi, ZHANG Xiao-ning. Application of Submodeling Method for Analysis for Deck Structure of Diagonal Cable-stayed Bridge with Long Span [J]. China Civil Engineering Journal, 2004, 37(6):30-34.

[16]邢中凯. 钢箱梁正交异性桥面板受力特性及计算方法分析研究[D]. 上海：同济大学, 2003.

XING Zhong-kai. Analysis of Mechanical Characteristics and Calculation Methods of Steel Box Girder’s Orthotropic Decks[D]. Shanghai: Tongji University, 2003.

[17]王新敏.ANSYS工程结构数值分析[M]. 北京：人民交通出版社, 2013.WANG Xin-min. ANSYS Numerical Analysis of Engineering Structures[M]. Beijing: China Communications Press,2013.[18]赵大亮, 李爱群, 丁幼亮,等. 基于子模型法的大跨斜拉桥扁平钢箱梁应力分析[J]. 计算力学学报, 2008, 25(3):326-332.

ZHAO Da-liang, LI Ai-qun, DING You-liang, et al. Stress Analysis on Steel-box Girder of Long Span Cable-stayed Bridge Based on Submodel Method[J]. Chinese Journal of Computational Mechanics, 2008, 25(3):326-332.

[19]RAFIEE A. Computer Modeling and Investigation on the Steel Corrosion in Cracked Ultra High Performance Concrete[D]. Kassel: University of Kassel, 2012.

[20]AALETI S, PETERSEN B, SRITHARAN S. Design Guide for Precast UHPC Waffle Deck Panel System, Including Connections, FHWA-HIF-13-032[R].Washington, D. C.: Federal Highway Administration, 2013.

Finite Element Analysis of Flexural Performance of Steel-UHPC Lightweight Composite Girder Deck

KONG Ling-fang1, SHAO Xu-dong1,2, LIU Rong3

(1.School of Civil Engineering, Hunan University, Changsha Hunan 410082,China;2. Hunan Provincial Key Laboratory of Wind and Bridge Engineering, Hunan University, Changsha Hunan, 410082, China;3.Hunan Provincial Communications Planning, Survey and Design Institute, Changsha Hunan 410008,China)

In order to deal with the problems that conventional steel-concrete composite girders have heavy self-weight and are susceptible to develop cracks in the concrete deck, we proposed a scheme of steel-UHPC lightweight composite girder which could significantly reduce the self-weight of the girder. To obtain the stress state of the deck of the new steel-UHPC lightweight composite girder, based on an example bridge under construction—the Shengtian Bridge, the longitudinal tensile and compressive stresses in the most unfavorable place of deck are calculated by the stress superposition method, the precise overall bridge FE method and mixed FE method respectively. The FE analysis was focused on the tensile stress and compressive stress in the concrete deck at the most unfavorable load positions. The analysis shows that (1) the calculation results obtained from the mixed FE method are quite close to the result derived from the precise overall bridge FE method, and the relative differences are within 4%; (2) the stresses calculated by the stress superposition method is higher than that of the precise overall bridge FE method, with a difference of 1.58 MPa to 3.80 MPa, and a relative difference of above 12%, which indicates that the result is conservative. In addition, by comparing the calculation result with the experimental result, it reveals that the maximum designed longitudinal tensile stress of UHPC deck is lower than the measured nominal tensile stress of UHPC that have a maximum crack width of 0.05 mm, and the longitudinal compressive stress is much less than the compressive strength of UHPC. Thus, the proposed steel-UHPC composite girder can meet the design requirements under the design loads.

bridge engineering; steel-UHPC lightweight composite girder; finite element analysis; stress of UHPC layer; stress superposition method; precise overall bridge finite element method; mixed finite element method

2016-01-25

国家自然科学基金项目(51178177)；交通运输部重大科技专项(2011318494160)；湖南省交通运输厅科技进步与创新项目计划(201437)

孔令方(1989-)，男，山东滕州人，硕士研究生.(15111391929@163.com)

10.3969/j.issn.1002-0268.2016.10.014

A

1002-0268(2016)10-0088-08