动载作用下半刚性基层沥青路面动力响应现场测试及数值模拟
张 静,魏连雨,马士宾,王 涛
(1.河北工业大学 土木与交通学院,天津 300401;2.天津市建筑科学研究院,天津 300193)
动载作用下半刚性基层沥青路面动力响应现场测试及数值模拟
张静1,魏连雨1,马士宾1,王涛2
(1.河北工业大学土木与交通学院,天津300401;2.天津市建筑科学研究院,天津300193)
依托实际工程,基于现场检测和三维有限元模拟技术,研究动载作用下半刚性基层沥青路面动力响应。首先,基于光纤光栅传感技术进行半刚性基层沥青路面动力响应现场测试,依据现场测试结果,确定有限元瞬态分析的动力学原理、荷载条件、边界条件及材料参数,建立沥青路面三维有限元模型;然后分析不同轴载及材料参数下路面结构内部的动力响应特征。结果表明,动载作用下,车速越低,路面结构受力状态越不利;纵向(行车方向)拉应变大于横向拉应变;随轴载的增大,路面结构的应变响应波动性增强,沥青层内部拉压应变交替变化剧烈;面层模量对路基顶压应变的影响程度显著于基层模量,基层模量则对面层底拉应变影响较大。
道路工程;沥青路面;光纤光栅传感技术;动力响应;应变;数值模拟
0 引言
截至2014年年末我国高速公路总里程达11.19万公里,跃居世界第一,其中公路养护里程占总里程90%以上。在已建成的高速公路沥青路面中,80%以上采用基于经典路面结构设计方法的半刚性基层沥青路面结构。这种利用静载代替车辆动荷载的设计方法所反映的路面结构应力应变关系,不能反映路面结构的实时受力状态,导致半刚性基层沥青路面没有达到设计使用年限就出现裂缝、坑槽、车辙等损坏现象,造成工作量繁重的养护工作[1]。因此,半刚性基层沥青路面动力响应研究成为沥青路面结构设计方法研究的重点和难点,同时,智能传感器在路面结构内部监测中的应用也成为道路领域的研究热点。目前现有的检测手段仅定性给出其损坏的程度,不能获取路面结构内部的实时应力应变状态,无法实现对路面结构内部的实时监测、损坏原因诊断以及损坏演化规律的研究[2]。本文采用基于光纤光栅传感技术的现场检测和三维有限元模拟技术,深入研究在移动荷载作用下,半刚性基层沥青路面结构动力响应,为沥青路面结构设计方法的进一步完善提供理论参考。
1 基于光纤光栅传感技术的现场试验
1.1试验路概况及传感器布设
光纤光栅(FBG)传感器具有灵敏度高、变异性小且与路面结构层协同变形良好的特点[3-5],本研究使用FBG传感器进行半刚性基层沥青路面结构内应变场现场检测。以某国道改造工程为依托铺设试验路,路面结构如图1所示。车辆荷载作用下半刚性基层沥青路面拉应变最大值出现在车道轮迹带处,因此将传感器埋设在车道右侧轮迹带基层及面层层底,FBG传感器、压力盒以及温度传感器的平面布置如图2所示。为获得车辆荷载作用下路面结构内径向、横向应变,FBG传感器沿径向、横向两个方向埋设,沥青面层底编号为A-1,A-2,基层底编号为B-1,B-2。通过现场试验得到半刚性基层沥青路面在移动荷载作用下的动力响应实测数据,用于对有限元模型进行验证。

图1 路面结构示意图及传感器纵断面布置图Fig.1 Schematic diagram of pavement structure and layout of sensor longitudinal profile
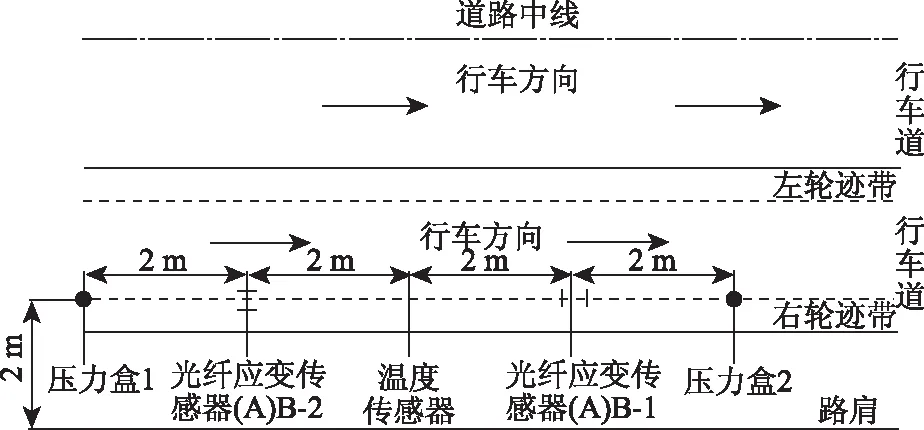
图2 传感器平面布置图Fig.2 Plan layout of sensors
1.2动载测试与分析
加载试验采用双后轴加载车,将轴重最大的中轴标定为标准轴载BZZ-100,采用电子地秤称量中轴轴重并通过压力盒校核,使两种方法测试结果一致。半刚性基层沥青路面动态应变场的测试使用SM130型光纤光栅解调仪(见图3),扫描频率1 kHz。

图3 SM130型光纤光栅解调仪Fig.3 SM130 FBG demodulator
动载试验设计20,30,50,60 km/h共4种不同车速,使加载车按4种规定车速通过测试点,由于环境影响及驾驶员操作的不稳定性,造成实际车速与规定车速之间存在偏差,由FBG传感器测定应变任意两波峰间的时间差,计算得加载车实际车速为27,34,57,63 km/h。由于车辆振动对路面结构的作用,采集得到数据具有波动性,利用Matlab进行插值去噪处理后,得到半刚性基层沥青路面应变时程图(见图4,拉应变为正)。
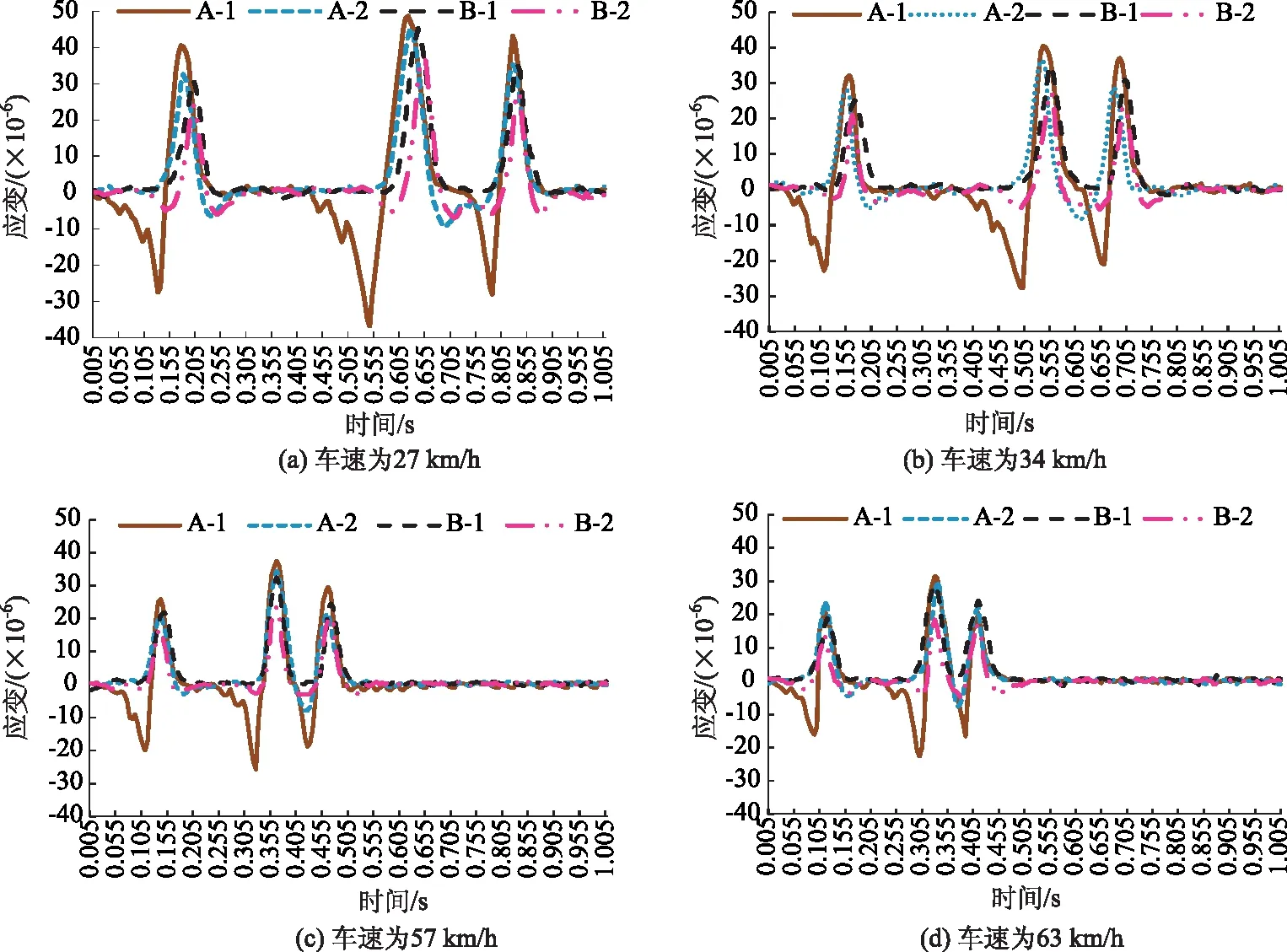
图4 不同车速下,路面结构动力响应时程Fig.4 Time histories of dynamic response of pavement structure at different speeds
由图4看出,移动荷载对半刚性基层沥青路面结构的作用具有明显规律性。动载作用下,半刚性基层底以拉应变为主;沥青面层底则先产生压应变,逐渐增大至峰值后突变为拉应变并迅速增长至峰值。图4清晰显示路面结构内应变场与荷载呈现同步变化,应变峰值与轴重成正比,与车辆车速成反比。由于动载作用时间短,路面结构变形不如静载作用下充分,随车速的增加,路面结构内应变峰值不断减小,应变场波动性明显减弱,荷载作用范围缩小。综上,车速越低,路面结构受力状态越趋于不利,因此车辆的启动、停车过程对路面各结构层应变的影响更为显著,同时表明FBG传感器能够准确快速地反映路面结构内应变场的实时变化。
2 半刚性基层沥青路面动力响应数值模型的建立
2.1半刚性基层沥青路面瞬态动力学平衡方程
依据弹性动力学基本理论动力响应,使用ANSYS有限元软件建立半刚性基层沥青路面三维实体模型时,半刚性基层沥青路面的有限元瞬态动力学平衡方程[6]为:
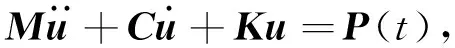
(1)

计算中车辆荷载采用AASHTO推荐的矩形汽车荷载如图5所示,轮胎接地压强为0.7 MPa。车辆移动荷载采用阶跃方式加载,荷载的移动通过设置随时间变化的不同单元实现,速度通过设置阶跃函数在其中任一单元上不同的持续时间实现。取等效轴载边长0.2 m作为加载模型中的最小单元边长,当加载车速为V时,荷载作用时间T计算方法见式(2):
(2)
式中,T为载作用时间;a为方形等效轴载边长;V为车辆行驶速度。
半刚性基层沥青路面结构的阻尼,通常采用瑞利阻尼假设[7]:
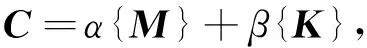
(3)
式中α,β为阻尼系数,可由动力系统的前两阶模态分析并按经验公式计算,通常可假设为0.05 和0.1[8-9]。
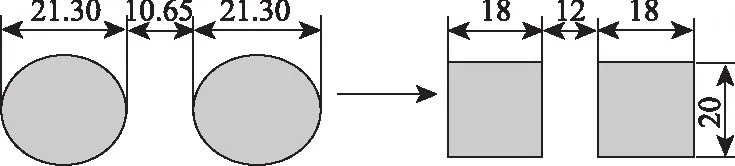
图5 车辆荷载模型(单位:cm)Fig.5 Vehicle load model (unit: cm)
2.2材料参数
模型采用应变实测现场路面结构,材料参数如表1所示。
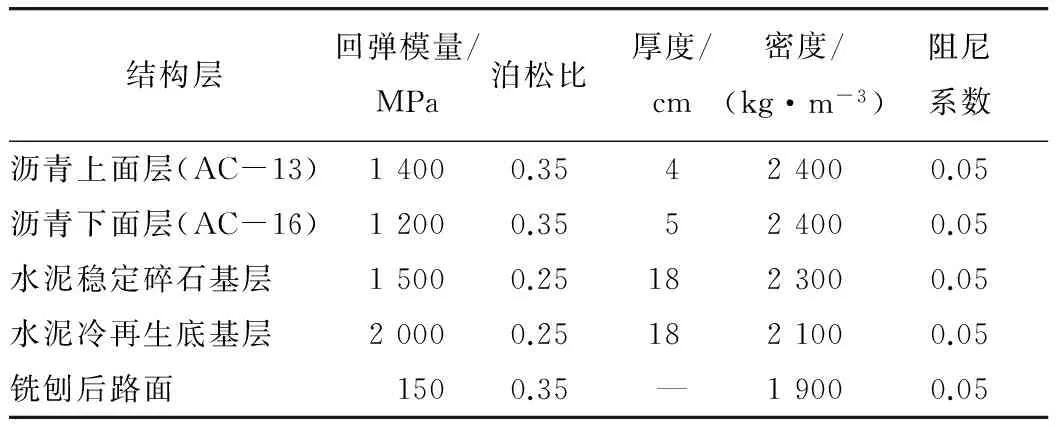
表1 路面结构模型参数Tab.1 Parameters of pavement structure model
2.3有限元模型
半刚性基层沥青路面三维有限元计算模型见图6,其中X为车辆行驶方向,Z为沿路面深度方向。考虑到计算效率和轮胎接地面积大小,模型尺寸长4 m,宽3.6 m,土基深度方向取3 m,模型使用SOLID45单元。半刚性基层沥青路面结构荷载扩散能力较强,为尽量减小边界效应,将模型土基尺寸扩大一倍;同时,为提高计算精度,对轮迹带区域内的网格进行加密处理。

图6 三维有限元模型Fig.6 Three-dimensional finite element model
在分析过程中作如下假设[10]:(1)假定结构层各层间完全连续接触,各层均由均质、各向同性的线性弹性材料组成,以弹性模量和泊松比表征弹性参数;(2)土基为水平方向无限延伸的半无限体,其余各层在水平方向上无限延伸,无纵向、横向位移,有厚度;(3)路面底部全约束。
2.4实测结果与模型结果的对比分析
将速度为60 km/h时加载车中轴(标准轴载)作用下路面结构应变场数据作为依据,对模型进行调整。有限元模型计算数据见图7,各结构层应变峰值的实测值和理论计算值见表2。可以看到,半刚性基层沥青路面三维有限元模型计算得到的路面结构内应变值与试验路实测值变化趋势基本一致,峰值误差为0.147~4.616 με,即本文所建有限元模型与路面结构实际受力情况基本相同。
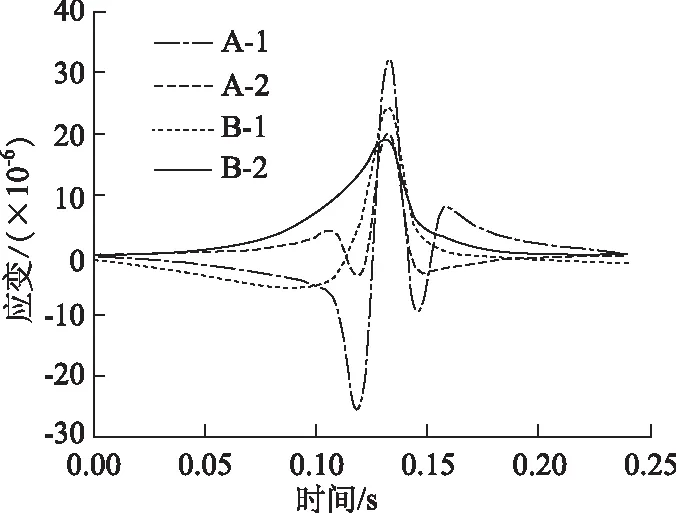
图7 车速60 km/h时,有限元模型动力响应时程Fig.7 Time history of dynamic response by finite element model when vehicle speed is 60 km/h表2 车速60 km/h时,路面结构内拉应变峰值Tab.2 Maximum tensile strain of pavement structure when vehicle speed is 60 km/h
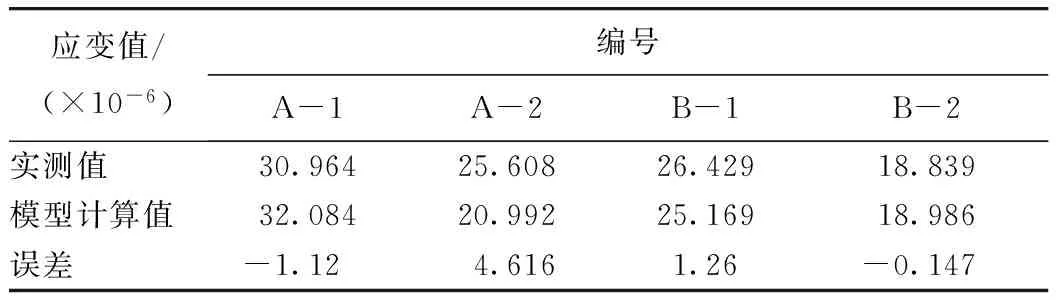
应变值/(×10-6)编号A-1A-2B-1B-2实测值30.96425.60826.42918.839模型计算值32.08420.99225.16918.986误差-1.124.6161.26-0.147
图7显示,半刚性基层沥青路面结构中,沥青面层底先出现压应变,随后压应变急剧变为拉应变,纵向拉应变最大值大于横向拉应变;基层底以拉应变为主,纵向拉应变最大值大于横向拉应变。综上所述,在半刚性基层路面结构中,与行车方向相同的纵向拉应变大于横向拉应变,即在同一结构层中,纵向拉应变是影响路面结构变形的主要因素。
3 半刚性基层沥青路面动力响应分析
为解决半刚性基层沥青路面的耐久性问题,我国半刚性基层长寿命路面设计中主要控制3个方面[11-12]:路基顶面压应变、沥青层底拉应变、半刚性基层底拉应变。结合2.4节结果,将路基顶面压应变、沥青层底纵向拉应变以及半刚性基层底纵向拉应变作为分析指标,研究材料特性对移动荷载作用下路面结构动力响应的影响,考虑我国近年超载现象严重,同时分析超载[13]对半刚性基层沥青路面结构内部应变场变化规律及动力响应特征。
3.1不同轴载对路面结构动力响应的影响
为探究不同轴载对半刚性基层沥青路面结构应变场的影响规律,将轮胎接地压强分别设定为0.5,0.7,0.9,1.1,1.3 MPa。图8给出了半刚性基层沥青路面结构动力响应随轴载的变化曲线。
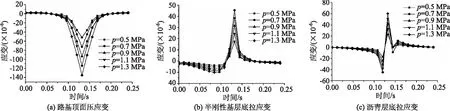
图8 不同轴载作用下路面结构动力响应Fig.8 Dynamic response of pavement structure under different loads
可以看到,路基顶面、沥青层底及半刚性基层底应变峰值均随轴载的增加而增加。沥青层底承受拉、压两种应变,拉、压应变峰值都随轴载的增加而增加,即应变由压变拉的变化过程更加剧烈,这种拉、压应变的交替作用是导致路面结构疲劳损坏的主要原因。综上所述,随轴载的增加,路面结构应变响应波动性增强,沥青层内部应变在荷载作用前后的拉压应变交替变化更加剧烈。
3.2材料参数对路面结构动力响应的影响
采用单因素分析法分别改变沥青层、水泥稳定碎石基层的材料模量,研究面层和基层材料特性对动载作用下路面结构内部力学响应的影响,为路面结构组合设计提供理论依据。计算中沥青面层模量取1 500~2 500 MPa,半刚性基层模量取800~1 600 MPa,取值范围包括了常见路面材料类型。图9给出了半刚性基层沥青路面结构应变峰值随模量的变化曲线。
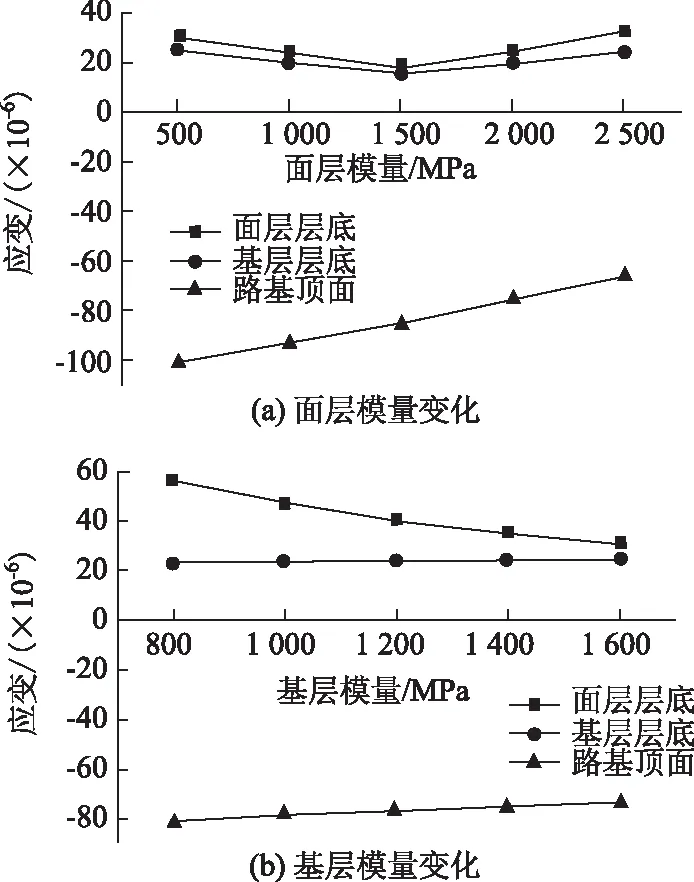
图9 路面结构应变峰值随模量的变化曲线Fig.9 Maximum strain curves of pavement structure varying with modulus
由图9(a)看到,随沥青面层模量的增加,路基顶压应变不断减小,面层层底和基层层底拉应变呈先减小后增大的变化趋势。图9(b)显示,随着半刚性基层模量的增加,沥青面层层底拉应变不断减小,基层底和路基顶应变变化不大。可以得到,面层模量对路基顶压应变的影响程度显著于基层模量;基层模量则对面层底拉应变影响较大。路面弯沉是路基和路面结构不同深度处竖向应变的总和,综上,若想减小路面弯沉,通过增大基层模量是得不偿失的,应在路面结构组合设计中适当增大面层模量;而在路面结构组合设计中,若基层选用较小模量值,需重点验算面层底拉应变是否与材料的容许抗拉强度相适应。
4 结论
(1)根据基于光纤光栅传感技术的现场应变测试结果,半刚性基层沥青路面结构内应变场与荷载呈现同步变化;随车速的增加,应变峰值不断减小,应变场波动性明显减弱,荷载作用范围缩小。
(2)根据有限元模型计算结果得到,在半刚性基层路面结构中,与行车方向相同的纵向拉应变大于横向拉应变,即在同一结构层中,纵向拉应变是影响路面结构变形的主要因素。
(3)移动荷载作用下,沥青面层模量对路基顶压应变的影响程度显著于基层模量,基层模量则对面层底拉应变影响较大。在路面结构组合设计中,若通过增大基层模量减小路面弯沉则得不偿失,应适当增大面层模量;若基层选用较小模量值,需重点验算面层底拉应变是否与材料的容许抗拉强度相适应。
[1]王保实. 移动荷载作用下半刚性基层沥青路面结构的动力响应研究[D].西安:西安建筑科技大学,2011.
WANG Bao-shi,Study on Dynamic Response of Asphalt Pavement Structure with Semi-rigid Base Course under Moving Load [D]. Xi’an: Xi’an University of Architecture and Technology, 2011.
[2]董泽蛟,曹丽萍,谭忆秋,等. 移动荷载作用下沥青路面三向应变动力响应模拟分析[J]. 土木工程学报,2009,42(4):133-139.
DONG Ze-jiao, CAO Li-ping, TAN Yi-qiu, et al. Analysis of the Dynamic Response of Three Directional Strains in Asphalt Pavement under Moving Vehicle Loads [J]. China Civil Engineering Journal, 2009, 42(4):133-139.
[3]谭忆秋,王海朋,马韶军,等. 基于光纤光栅传感技术的沥青路面压实监测[J]. 中国公路学报,2014,27(5):112-117.
TAN Yi-qiu, WANG Hai-peng, MA Shao-jun, et al. Asphalt Pavement Compaction Monitoring Based on Fiber Grating Sensing Technology [J]. China Journal of Highway and Transport, 2014, 27(5):112-117.
[4]谭忆秋,董泽蛟,田庚亮,等. 光纤光栅传感器与沥青混合料协同变形评价方法[J]. 土木建筑与环境工程,2009,31(2):100-104.
TAN Yi-qiu, DONG Ze-jiao, TIAN Geng-liang, et al. Evaluating Method of the Coordination Deformation between Asphalt Mixture and Fiber Bragg Grating Sensor[J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(2):100-104.
[5]张静,魏连雨,马士宾,等. 基于光纤光栅技术的半刚性基层力学响应测试分析[J]. 传感技术学报,2016,29(3):326-331.
ZHANG Jing, WEI Lian-yu, MA Shi-bin, et al. Experiments and Analysis on the Mechanical Response of the Semirigid Substrate Using Fiber Bragg Grating Sensing Technology[J]. Chinese Journal of Sensors and Actuators, 2016, 29(3):326-331.
[6]李江,王晓涛,余胜军. 不同车速下沥青路面结构的动力响应[J]. 公路交通科技,2015,32(8):6-11.LI Jiang, WANG Xiao-tao, YU Sheng-jun. Dynamic Responses of Asphalt Pavement Structure to Different Vehicle Speeds[J]. Journal of Highway and Transportation Research and Development, 2015, 32(8):6-11.
[7]李皓玉,杨绍普,李韶华. 车、路的相互作用下沥青路面动力学特性分析[J]. 振动与冲击,2009,28(4):86-89,102,205.
LI Hao-yu, YANG Shao-pu, LI Shao-hua. Dynamical Analysis of an Asphalt Pavement due to Vehicle-road Interaction[J]. Journal of Vibration and Shock, 2009, 28(4):86-89,102,205.
[8]董泽蛟,刘美丽,郑好,等. 考虑横观各向同性特性的沥青路面动力学分析[J]. 中国公路学报,2012,25(5):18-23.
DONG Ze-jiao, LIU Mei-li, ZHENG Hao, et al. Dynamic Mechanical Analysis of Asphalt Pavement Based on Cross-isotropic Properties [J]. China Journal of Highway and Transport, 2012, 25(5):18-23.
[9]陈新. 机械结构动态设计理论方法及应用[M]. 北京:机械工业出版社,1997: 100-123.
CHEN Xin. Mechanical Structure Dynamic Design Theory Methods and Application [M]. Beijing :China Machine Press,1997:100-123.
[10]杨博. 基于有限元方法的沥青路面车辙影响因素分析及其应用研究[D]. 西安: 长安大学,2010.
YANG Bo. Influencing Factors of Asphalt Pavement Rutting Based on Finite Element Method and Applications [D]. Xi’an: Chang’an University,2010.
[11]薛忠军,王春明,张伟,等. 半刚性基层长寿命路面结构和材料设计研究[J]. 公路交通科技,2015,32(10):37-42,56.
XUE Zhong-jun, WANG Chun-ming, ZHANG Wei, et al. Research on Pavement Structure and Material Design of Semi-rigid Base Long-life Pavement[J]. Journal of Highway and Transportation Research and Development, 2015, 32(10):37-42,56.
[12]易向阳. 长寿命柔性路面技术的探讨与应用[J]. 公路交通科技,2015,32(6):25-31.
YI Xiang-yang. Discussion and Application of Long-life Flexible Pavement Technology[J]. Journal of Highway and Transportation Research and Development, 2015,32(6):25-31.
[13]李霖,闫瑾. 超载下倒装式沥青路面结构有限元分析[J]. 公路交通科技,2015,32(8):25-28,33.LI Lin,YAN Jin. Finite Element Analysis of Asphalt Pavement Structure with Inverted Base Layer under Overload Load[J]. Journal of Highway and Transportation Research and Development, 2015,32(8):25-28,33.
Field Test and Numerical Simulation of Dynamic Response of Semi-rigid Base Asphalt Pavement under Moving Vehicle Load
ZHANG Jing1,WEI Lian-yu1,MA Shi-bin1,WANG Tao2
(1. School of Civil Engineering and Transportation, Hebei University of Technology, Tianjin 300401, China;2. Tianjin Research Institute of Building Science, Tianjin 300193, China)
Relying on the real project, the dynamic response of semi-rigid base asphalt pavement under moving vehicle load is studied based on the field test and 3D finite element simulation. First, the field test of the dynamic response of semi-rigid base asphalt pavement is conducted using fiber grating sensing technology. The dynamic theory, the moving vehicle load condition, the boundary condition and the structural parameters for the FE transient analysis are determined according to the field test result, and a 3D finite element model of the asphalt pavement is established. Then, the internal dynamic response feature of the pavement under different axle loads and material parameters are analysed. The result indicates that (1) under moving vehicle load, the stress state of the pavement tends to adverse with the decreasing of vehicle speed; (2) the longitudinal (the same as the driving direction) tensile strain is greater than the transverse tensile strain; (3) as the load increases, the volatility of strain response of the pavement is enhanced, and the tensile and compressive strains in the asphalt layer change alternately and dramatically; (4) the effect of surface modulus on the compressive strain on the top of subgrade is more significant than the base modulus, but the base modulus has a great impact on tensile strain at the bottom of surface.
road engineering; asphalt pavement;fiber grating sensing technology; dynamic response; strain; numerical simulation
2015-12-30
河北省高等学校科学技术研究项目(ZD2014099);河北省教育厅青年基金项目(QN2015036)
张静(1988-),女,河北张家口人,博士研究生.(13920530692@126.com)
10.3969/j.issn.1002-0268.2016.10.004
U416.217
A
1002-0268(2016)10-0019-06

