不完整信息下城市交通速度修复算法
钟会玲,吴昊旻,陈迎迎,孙万菊
(浙江浙大中控信息技术有限公司,浙江杭州 310053)
不完整信息下城市交通速度修复算法
钟会玲,吴昊旻,陈迎迎,孙万菊
(浙江浙大中控信息技术有限公司,浙江杭州 310053)
通过深入分析不完整信息数据的交通流路段速度,提出神经网络与线性回归组合模型的速度修复算法,利用相关性分析在交通流数据中找到路段速度在时间和空间上影响因素,将在时间上影响路段速度的因素作为神经网络模型的输入变量,将在空间上影响路段速度的因素作为神经网络模型的输入变量,分别输出路段速度预测结果,将以上模型预测结果作为线性回归模型输入变量,最终得出路段速度二次预测结果。
交通流;路段速度;线性回归;神经网络;线性相关
将时间和空间组合的相关性引入交通数据分析可以较好地解决单纯依赖时间序列和空间分析存在的问题,因此,本文引入时空组合模型对路段速度进行修复的方法,解决不完整信息下城市交通速度修复问题。
1 方法与数据
1.1方法
(1)BP神经网络模型
神经网络的训练过程是一个不断向样本学习的过程,学习的目的是通过不断调整网络权值得到较小的预测误差,BP神经网络模型是一种以反向传播算法学习的前馈式多层感知机,采用参数优化方法实现网络权值的调整,参数优化是在一个特定模型结构M中,利用数据D优化模型参数,以求得使损失函数L(W)=L(W│D,M)达到最小时的模型参数W。损失函数L(W)的优化是以迭代方式体现,其特点是采用梯度下降法,每个时刻都本着使损失函数减小最快的原则调整网络权值,不同类型问题的损失函数形式是不同的,一般预测问题的损失函数主要取决于预测模型和实际数据的误差函数。
(2)线性回归模型
回归分析是研究随机变量之间的相关关系的一种统计方法,其用意是研究一个被解释变量(又称因变量)与一个或多个解释变量(又称自变量)之间的统计关系。
论文利用的模型为多元线性回归,将所选变量全部强行进入回归,其线性模型即
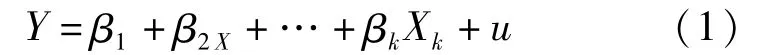
(3)相关分析
相关分析是研究两数值型变量线性相关性的常用方法,需经过以下两个步骤:第一,计算Pearson样本相关系数r;第二,对样本来自的两总体是否存在显著线性关系进行检验。
Pearson样本相关系数即样本简单相关系数,反映变量间线性相关程度的强弱;对样本来自的两总体是否存在显著线性关系进行检验,首先假设两总体零线性相关,其次计算Pearson相关系数的检验统计量t及其对应的概率P,最后比较P与显著性水平通常设为0.05得出是否线性相关结果。
论文通过运用相关性分析在交通流数据中找到路段速度在时间和空间上影响因素,利用神经网络模型输出路段速度预测和线性相关性结果,利用线性回归模型得出路段速度二次预测结果,并利用测试集验证结果,得出较高的线性相关度,表明该模型方法适用于城市交通速度修复。
1.2数据
为了验证所提方法的有效性,以2015年浙江省绍兴市交通流数据为研究对象,研究区域范围现安装有73个路口电子警察设备,可形成路段数为223,其中141个路段有数据,该电警数据包括车辆信息,车辆经过地点、方向,车道号及经过时间,利用该每5分钟数据形成车辆经过某路段数据,并通过删除滞留车辆数据,绕弯车辆数据达到清洗数据的目的,最后得出每5分钟路段速度,论文选取以万商路上笛扬路到金柯桥大道路段为研究对象,其中采用2015年3月至8月半年交通流数据处理完成后作为历史数据,训练集和测试集采用2015年9月至11月三个月交通流数据,分析时间上模型采用连续5分钟同一路段速度数据,分析空间上模型采用同一时间段不同路段,其中不同路段数据由于设备老化或者由于未安装只能采取部分不完整路段速度数据。
1.3实验流程
原始交通流数据经过处理后形成路段过车数据,清洗干净后计算出路段速度,然后通过混合模型分析数据,具体实验流程如图1所示,包括5个步骤:

图1 不完整信息下城市交通速度修复算法实验流程
步骤一:原始交通流数据经过处理后形成路段过车数据,清洗干净后计算出路段速度,同时通过绘图得出速度的时间分布特性。
步骤二:利用相关分析分别得出路段速度在时间上和空间上的影响因素。
步骤三:利用BP神经网络算法分别得出路段速度在时间和空间上与其影响因素间关系。
步骤四:利用测试集分别验算时间和空间上计算得出的实时路段速度结果的准确率,同时利用线性回归得出时间和空间上的路段速度结果与实际实时路段速度间线性关系结果。
步骤五:利用测试集验算混合模型得出的实时路段速度结果的准确率,最后对比三种准确率。
2 结 果
2.1数据清洗结果与速度时间分布特性结果
论文以2015年9月至11月万商路上的笛扬路到金柯桥大道的数据为研究对象,分析期间一周数据清洗前和清洗后数据量变化,该研究路段某一周内流量有28 702辆(已化为小车当量数),清洗后加入路段速度计算的数据有14 439行,有效数据占比81.3%,平均到每天每5分钟实时有效数据偏低,必然会出现缺失数据,此处研究对象整体缺失率为45.54%,其中包括晚上数据缺失,白天数据缺失率为19.37%。
同时分析历史交通路段速度在连续一周内的时间分布特性。交通路段速度的时间分布特性如图2所示,由图2可以看出,在7:00-9:00和17:00-19:00的时段内万商路某一路段交通路段速度相对较低,呈现出早晚高峰的特征,且在连续的几个工作日内路段速度变化大体相似,即在时间维度上具有相似性。
2.2时空相关分析结果
利用路段速度时间上的交通特性,在时间上,利用两数值型变量线性相关模型,将历史速度以及该时刻之前之后最近5个时刻速度输入,得到上两个时刻与历史速度与当前时刻速度最为强相关。

图2 交通路段速度的时间分布
在空间上,利用两数值型变量线性相关模型,将该路段速度和对应其他路段速度输入,得到该路段速度与其他相邻或相交的5条路段速度最为强相关,如图4,其中93speed-3为目标路段变量,其他代表输入路段自变量。其中红色为目标路段,绿色为相关路段。

图3 时间上速度强相关结果

图4 空间上速度强相关结果
2.3时空BP神经网络算法结果
在上一步得出的时空相关分析结果基础上,利用BP神经网络算法利用训练集分别得出在时间上历史路段速度、上一个时刻路段速度与当时当刻路段速度关系,训练集线性相关可信度为87.9%;在空间上目标路段速度与该区域对应时刻其他路段关系,训练集线性相关可信度为86.6%。
利用测试集分别验证时空关系结果,得出时间上利用BP神经网络算法得出的线性相关可信度为90.4%,且预测值的平均绝对误差为3.22 km/h;空间上利用BP神经网络算法得出的线性相关可信度为88.1%,且预测值的平均绝对误差为2.99km/h,时间上神经网络预测值与实际值对比结果如图5,空间上神经网络预测值与实际值对比结果如图6。

图5 时间上神经网络预测值与实际值对比结果
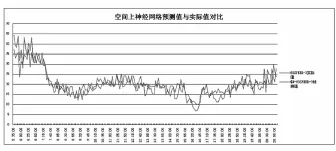
图6 空间上神经网络预测值与实际值对比结果
2.4时空线性回归结果
在上一步得出的时空BP神经网络算法结果基础上,将训练集利用线性回归得出时间上关系结果、空间上关系结果两种结果与路段速度关系。
利用测试集验证回归模型结果,得出利用BP神经网络算法与线性回归混合模型得出的训练集线性相关可信度为89.4%,测试集线性相关可信度为91.7%,且预测值的平均绝对误差为2.70 km/h;相比单独从空间和时间上BP神经网络模型,得出的路段行程速度的平均绝对误差降低0.3~0.5 km ·h-1,混合模型预测值与实际值对比结果如图7,采用组合模型进行速度插补如图8。
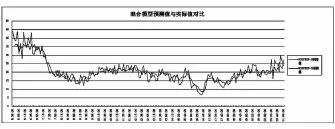
图7 混合模型预测值与实际值对比结果
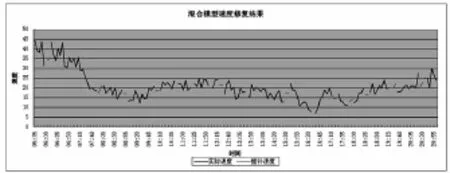
图8 混合模型速度修复结果
3 讨 论
首先论文为找到路段速度的影响因素,分别在时间和空间上对影响因素与路段速度进行相关性分析,从而得到在时间上上两个时刻与历史速度与当前时刻速度最为强相关,在空间上得到该路段速度与其他五条路段速度最为强相关。
其次论文在模型选取上,在时间和空间建模得出的结果下,再利用线性回归模型,将时间和空间所得模型作为输入变量,重新与路段速度得出新的线性关系,并且该组合模型得出的结果相比单独神经网络模型准确率偏高,说明模型选择合理。
最后从研究结果看,空间上与目标路段速度相关的路段,基本上是相邻、对面逆向路段或者与该路段相交的路段,说明上下游的交通流之间有相互影响,且影响较为明显,时间和空间上路段速度与历史速度以及上两个时刻以及其他相邻或相交路段相关,在当时当刻速度缺失的情况下可选择利用组合模型预测出来的值进行插补。
4 结 论
论文通过有效分析得出,在时间上路段实时速度与对应历史速度以及实时的上一时刻速度具有强线性相关,在空间上路段速度与相邻路段和其他具有相同特性的路段具有强线性相关,并利用测试集验证,最后空间和时间上的影响因素组合成新的线性模型得出结果,再次利用测试集验证,其实验数据证明,将空间和时间上的影响因素组合成新的线性模型得出结果较单独模型得出速度结果具有更高的准确率,提高交通预测的准确性。
论文研究路段速度在空间上同一时间具有强线性相关的路段,可以作为目标路段速度缺失修复的方法,同时也可以研究路段速度在空间上不同时间具有强线性相关的路段,论文研究结果仅对时间跨度较小的缺失数据有效。不过论文研究结果可以完善交通数据库,提高交通预测的准确性,同时一定程度上辅助管理部门了解实时城市交通运行情况,从而对经常拥堵路段采取应对措施。
如果想要修复时间跨度较大的路段速度数据可以通过以下方法,当预测目标路段在下一时段的速度及运行拥堵情况时,可以根据上一时刻与之相关的路段速度或者流量预测出来,该方法有待进一步研究,预期研究结果可以辅助管理部门为将来可能导致的严重拥堵路段提前做好准备与部署工作。
[1] 蒋锐,王均.道路交通流数据检验与修复方法[J].交通与计算机,2006,24(6):65-67.
[2] 瑞斯.琼.数理统计与数据分析.田金方,译[M].北京:机械工业出版社,2009:340-341.
[3] 陈封能,斯坦巴克.数据挖掘导论[M].范明,译.北京:人民邮电出版社,2011:222-223.
U492
C
1008-3383(2016)09-0166-03
2016-03-15
钟会玲(1989-),女,硕士,研究方向:交通运输。

