堆积型多孔介质中流动的真实模拟

康锐文，徐江荣

(杭州电子科技大学能源研究所，浙江 杭州 310018)



堆积型多孔介质中流动的真实模拟

康锐文，徐江荣

(杭州电子科技大学能源研究所，浙江 杭州 310018)

固体小球排列形成的多孔介质区域是一种典型的多孔介质模型，对多孔介质区域内的流动进行真实的数值模拟，来替代传统的宏观模拟.通过真实模拟获得压力、速度等流动状态的复杂变化，与传统的多孔介质宏观模拟对比，真实模拟更能反映湍流流动的实际情况.

多孔介质；数值模拟；湍流

0　引　言

多孔介质是由多相物质所占据的空间，也是多相物质共存的一种几何体；多孔介质中的流体流动在化工、石油工程、地质学中普遍存在.1856年，文献[1]开创了这方面的研究，大多数学者采用的是宏观模型对多孔介质内的流动进行数值模拟研究[2-3]，使用这种方法，空隙中的流动、传热、传质等一系列的信息会被忽略掉，对研究造成不便.

近年来，随着计算机技术的发展，对多孔介质中流体流动真实模拟随之兴起，文献[4-5]用N-S方程模拟了周期性排列的方形物体微观单元内湍流流场，对水和空气流过细微多孔介质进行了直接数值模拟.文献[6]利用13-Bit正六边形多速格子气自动机方法对多孔介质流动的模拟进行研究.文献[7]利用光滑粒子动力学(SPH)对基于空隙尺度下的多孔介质模型进行了数值模拟.文献[8-9]用大涡模拟对多孔介质内流场进行真实模拟.但上述模拟的空间尺度小，并且没有与宏观模拟做对比.

本文建立了多孔介质堆积床内流动的物理模型与数学模型，取一多孔介质堆积床的中心截面为研究域，从多孔介质的微观角度出发对空隙中的气体流动进行真实模拟.模拟的空间范围较大，流动区域更加复杂，并与相同的工况条件下的宏观模拟结果进行了对比分析.通过真实模拟可以分析宏观模拟的缺陷，了解多孔介质内部流动的详细情况.

1　数学模型

图1　多空介质模型网格示意图

真实模拟对象为一个颗粒堆积床的中心截面，长400 mm，内径80 mm，模型共划分为43 000个网格，多孔介质系统的二维物理模型的周期性网格截面如图1所示.在模型中假设：颗粒是均匀分布的，模型为平面二维结构，忽略质量力作用，气体为理想不可压缩气体，多孔介质是不可渗透的.

虽然多孔介质内流动雷诺数很低，通常只有几百，但多孔介质中的湍流转变点不同于管道流.文献[10]认为雷诺数大于80时，需要考虑湍流效应，当雷诺数大于160时，必须考虑湍流作用，故采用标准的k-ε湍流模型做为本文的数学模型，控制方程如下[11]：

(1)

宏观模拟方法中，一般是在式(1)中的动量方程中增加阻力源项，阻力源项方程可简化为：

(2)

真实模拟与宏观模拟在相同假设条件的基础上进行如下的同工况计算：

入口边界条件：空气T0=300 ℃,u=uin,v=0.

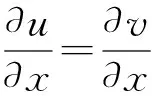
壁面边界条件：在求解动量方程时，假定混合气体在燃烧器的壁面内是壁面无滑移和不可渗透.

计算采用CFD软件包Fluent6.3进行求解，数值模拟采用压力基求解器对稳态连续方程进行求解，空间采用二阶迎风差分，选择SIMPLE算法对压力、速度进行修正[12].

2　结果分析

孔隙率为0.5，进口速度为0.4 m/s的工况条件下，流体在堆积床中轴线方向上不同位置处的压力分布如图2所示.对比图2中的3张图，不同位置处2个模型均出现了明显的压降，并且宏观模型的相同位置处压力略高于本文模型，这是因为在宏观模型中默认使用的物理流速为表观流速与孔隙率的比值，是一个均值.而在本文真实模拟模型中，因为固相的不流通性造成局部流通区域速度高于宏观模型的物理流速，由伯努利定理可知，真实模拟的径向位置压力略低于宏观模型，从而也验证了真实模拟的有效性.

图2　不同切面处径向气体压力分布

真实模拟的速度云图与一个固体颗粒单元周围的速度矢量图如图3所示.由图3可以看出，在多孔介质的空隙中，流体流动的最大速度在2个颗粒之间的间隙部分，这是因为固相颗粒对流动的阻隔，并且在靠近颗粒壁面附近，由于壁面的粘性作用，明显形成了一个速度梯度分布.

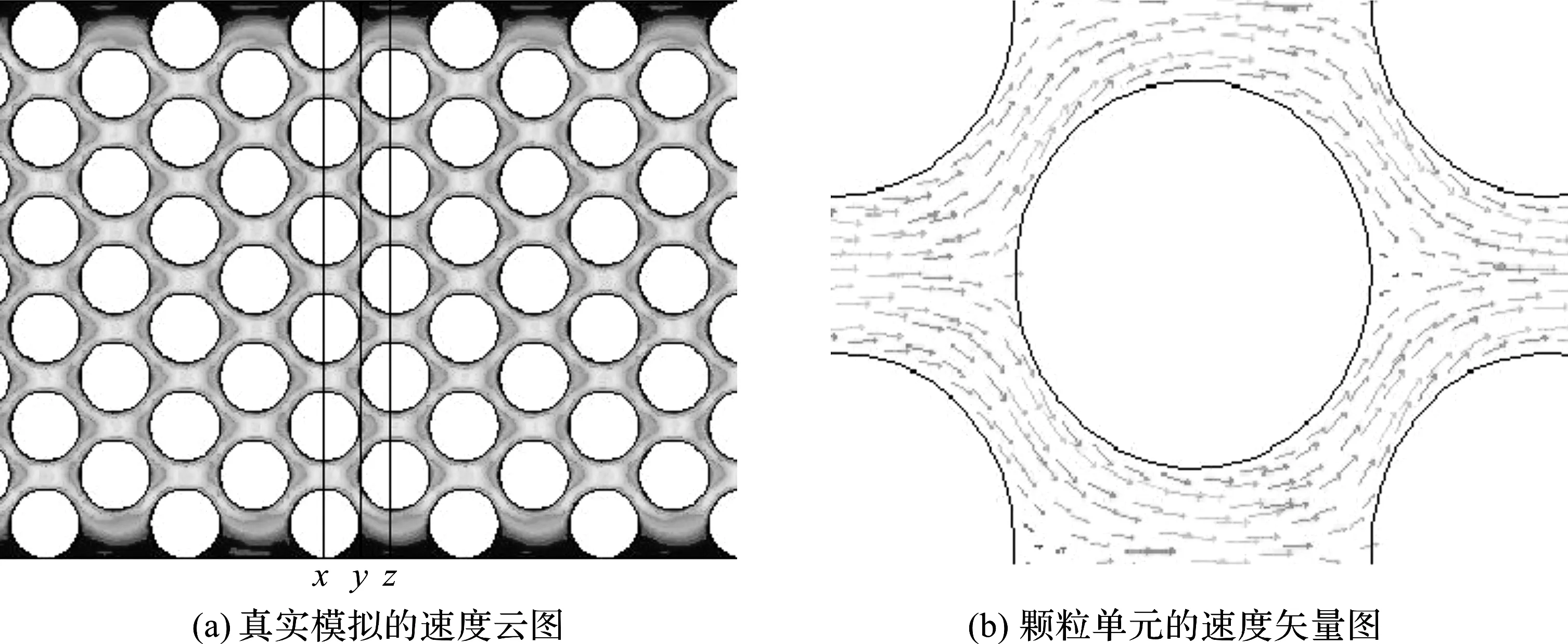
图3　真实模拟速度云图与矢量图

真实模型中轴向3个不同特征位置切面(图3中x，y，z)处的速度分布如图4所示.从图4中可以看出，不同位置处的速度体现着各自的特征，这种不同特征的出现是由于多孔介质中固相的存在，这不是宏观模型中阻力源项所能体现出来的.为了验证真实模型的有效性，本文还计算了在x处真实模型与宏观模型的的质量流率，分别为0.036 89 kg/s与0.039 2 kg/s，误差在可接受范围内.

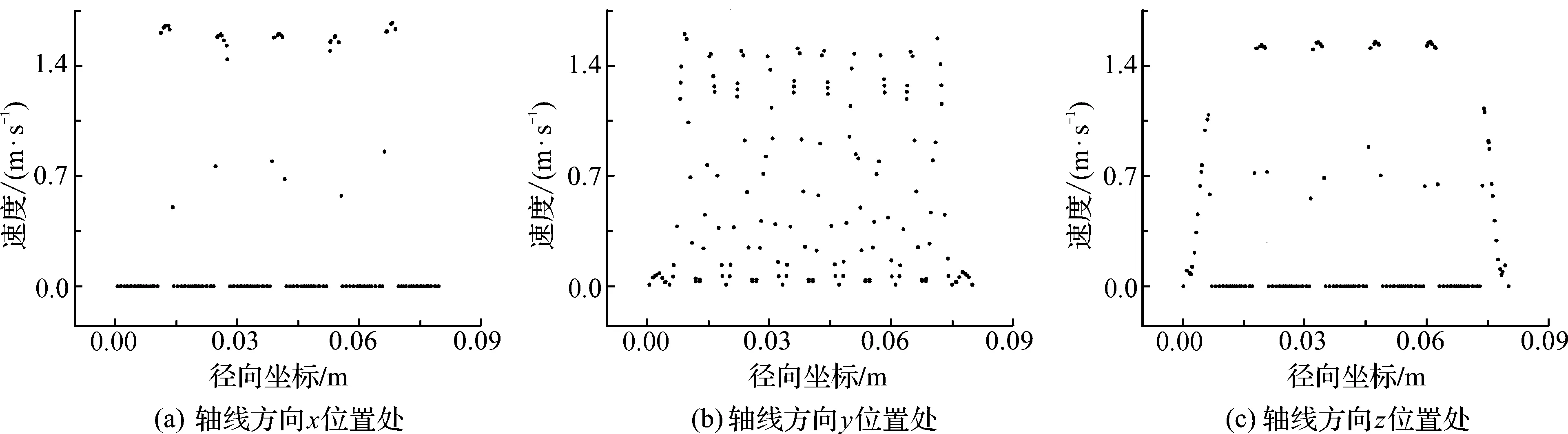
图4　径向速度分布

图5、图6分别为宏观模型与真实模型的湍动能耗散率与湍动能强度在模型轴向中心处切面的径向分布.从图5、图6中可以看出宏观模型与真实模型的差异，造成这种差异的首要原因是，在真实模拟中，多孔介质固相会对流体流动产生很大的扰动，并且这种扰动会加剧流动中的湍流作用.图5、图6中，真实模拟的湍动能耗散率和湍动能强度与宏观模型的相比出现的不稳定性体现了多孔介质固相空隙的弯曲性与随机性，更加贴近实际情况，从而能够更好地模拟出多孔介质中的流动.

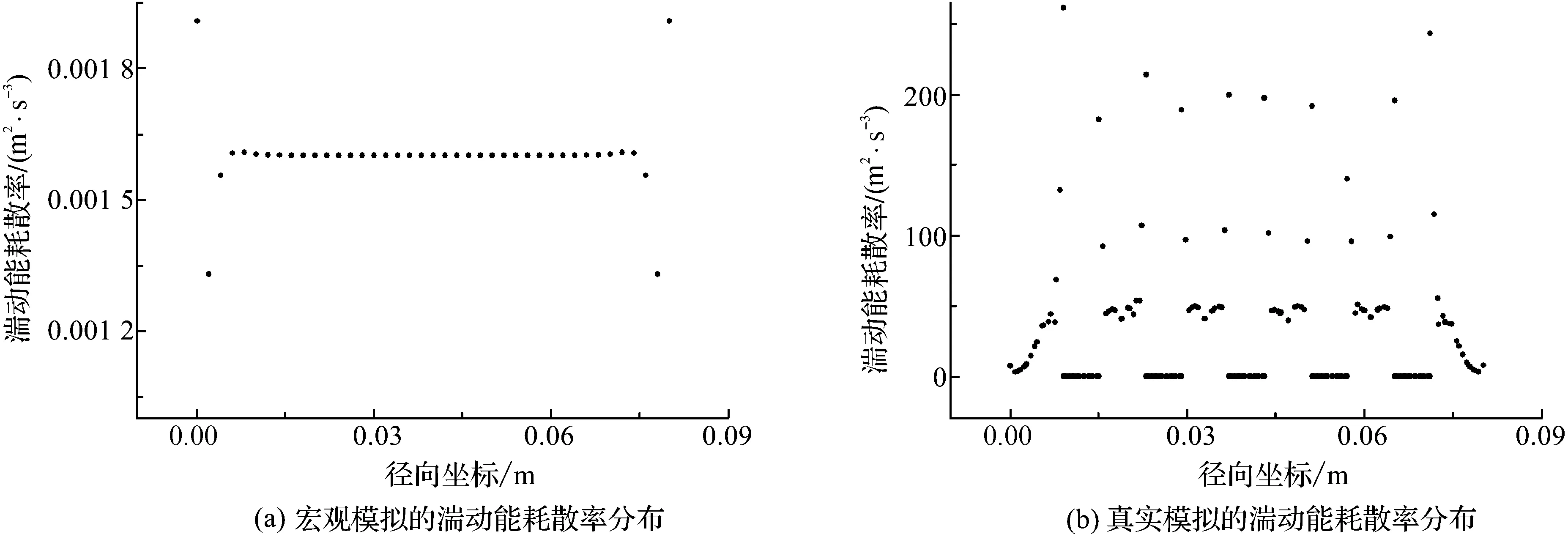
图5　径向气体湍动能耗散率分布

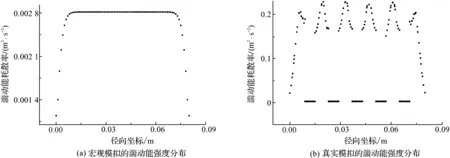
图6　径向气体湍动能耗散率分布

3　结束语

多孔介质的真实模拟模型与宏观模型相比较，能更加精确地显示不同区域处的压力损失和压强变化，不过真实模拟的计算量较大.所以，在计算条件允许的前提下，本文提出的真实模拟模型能更加准确地描述不同位置的物理量变化.

[1]NIELD D A,BEJAN A.Convection in Porous Media[M].New York：Springer Velag,1999:23-65.

[2]崔海清,郑晓松,王东城,等.粘弹性流体在多孔介质中的流动压降[C]//第十届全国海事技术研讨会.2005:549-555.

[3]GASMI S, NOURI F Z. Numerical simulation for two-phase flow in a porous medium[J].Boundary Value Problems,2015,2015(1):1-10.

[4]KUWAHARA F, KAMEYAMA Y,YAMASHITA S,et al.Numerical modeling of turbulent flow in porous media using a spatially periodic array[J].Journal of Porous Media,1998,1(1):47-55.

[5]XU R N, JIANG P X. Numerical simulation of fluid flow in microporous media[J].International Journal of Heat and Fluid Flow,2008,29(5):1447-1455.

[6]郑忠,高小强,石万元.多孔介质中流体流动的格子气自动机模拟[J].化工学报,2001,52(5):406-409.

[7]李维仲,赵月帅,宋永臣.多孔介质孔隙尺度下不可压缩流体流动特性SPH模拟[J].大连理工大学学报,2013,53(2):189-193.

[8]KUWATA Y, SUGA K. Large eddy simulations of pore-scale turbulent flows in porous media by the lattice Boltzmann method[J].International Journal of Heat and Fluid Flow,2015,55:143-157.

[9]SHAMS A, ROELOFS F, KOMEN E M J, et al. Large eddy simulation of a randomly stacked nuclear pebble bed[J].Computers & Fluids,2014,96(5):302-321.

[10]KUWAHARA F, YAMANE T, NAKAYAMA A. Large eddy simulation of turbulent flow in porous media[J]. International Communications in Heat and Mass Transfer,2006,33(4):411-418.

[11]徐江荣，裘哲勇.热流过程的数学模型和数值模拟[M].北京：国防工业出版,2012:21-22.

[12]陶文铨.数值传热学[M].西安：西安交通大学出版社，2001:207-245.

Realistic Numerical Simulation for Porous Media Flow in Packed Bed

KANG Ruiwen, XU Jiangrong

(InstituteofEnergy,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Porous medium field arranged by solid balls is a typical flow. The actual numerical simulation of the flow in the porous medium is carried out to instead of traditional macro simulation. The pressure, velocity and the other are obtained to describe porous media flow field by the actual numerical simulation method. Compared with the results of traditional macro simulation method, it is shown that the actual simulation method can reflect the actual situation of the turbulent flow.

porous media; numerical simulation; turbulent flow

10.13954/j.cnki.hdu.2016.05.013

2015-12-16

康锐文(1989-)，男，河南巩义人，硕士研究生，动力机械热流理论与数值模拟.通信作者：徐江荣教授，E-mail:jrxu@hdu.edu.cn.

TK16

A

1001-9146(2016)05-0068-05